Calibrating the Mean-Reversion Parameter in the Hull-White Model Using Neural Networks

Abstract

Interest rate models are widely used for simulations of interest rate movements and pricing of interest rate derivatives. We focus on the Hull-White model, for which we develop a technique for calibrating the speed of mean reversion. We examine the theoretical time-dependent version of mean reversion function and propose a neural network approach to perform the calibration based solely on historical interest rate data. The experiments indicate the suitability of depth-wise convolution and provide evidence for the advantages of neural network approach over existing methodologies. The proposed models produce mean reversion comparable to rolling-window linear regression’s results, allowing for greater flexibility while being less sensitive to market turbulence.

1 Introduction

Stochastic models for the evolution of interest rates are a key component of financial risk management and the pricing of interest rate derivatives. The value of these products is enormous, with the outstanding notional amount currently being in the order of hundreds of trillions of US dollars [1]. One of the most widely used interest rate models is the Hull-White model, introduced in [2].

As with every computational model, the performance of the Hull-White model is significantly affected by its parameters and an improper calibration may lead to predictive inconsistencies. Specifically, the speed of mean-reversion can influence notably its results; a small value may produce more trending simulation paths, while a larger value can result in steady evolution of the interest rate. If the calibrated value does not reflect the actual market conditions, this may result in unrealistic estimates of risk exposure.

Neural networks have been proposed for the calibration of the speed of mean-reversion and volatility [3, 4], as they are able to learn more complicated structures and associations in comparison to linear models. The existence of such structures is apparent, considering the relations described by the term structure of interest rate. Using neural networks to estimate variables for explicit computational models enables the experimentation with more complex and larger datasets, which can ultimately improve their performance.

The inability of simple models to exploit complex associations is perceived as an opportunity to expand the current body of research. We contribute a novel calibration method, with neural models that handle multiple historical input points of several parallel time series. Given the wide use of interest rate models and the data limitations, a future extension of neural models to exploit common features from several datasets is deemed crucial.

The rest of this paper is organized as follows. In Sect. 2 we summarize the basic features of the underlying models and methodologies that will be used. Additionally we outline several approaches related to mean-reversion calibration. In Sect. 3 we study the Hull-White model. In Sect. 4 we discuss the proposed neural network approach and the evaluation. Finally, in Sect. 5 we present our results and in Sect. 6 we summarize our findings.

2 Background and Related Work

2.1 Hull-White Interest Rate Model

The model we consider, describes interest rate movements driven by only a single source of risk, one source of uncertainty, hence it is one-factor model. This translates in mathematical terms having only one factor driven by a stochastic process. Apart from the stochastic term, the models are defined under the assumption that the future interest rate is a function of the current rates and that their movement is mean reverting. The first model to introduce the mean reverting behaviour of interest rate was proposed by Vasicek [5]. The Hull-White model is considered its extension and its SDE reads:

$$\begin{aligned} dr(t)=( \theta (t) - \alpha r(t))dt + \sigma dW(t) \end{aligned}$$

(1)

where $\theta$ stands for the long-term mean, $\alpha$ the mean reversion, $\sigma$ the volatility parameter and W the stochastic factor, a Wiener process. Calibrating the model refers to the process of determining the parameters $\alpha$ and $\sigma$ based on historical data. $\theta (t)$ is generally selected so that the model fits the initial term structure using the instantaneous forward rate. However, its calculation involves both the volatility and mean-reversion, increasing the complexity when both are time-dependent functions.

Studying the Eq. (1) we observe the direct dependence on previous instances of interest rate which become even more obvious if we consider that $\theta$ indirectly relies on the term structure of interest rate as well. Clearly this model incorporates both temporal patterns, expressed as temporal dependencies and the market’s current expectations, while the mean reversion term suggests a cyclical behaviour, also observed in many other financial indicators.

The concept of mean reversion suggests that the interest rates cannot increase indefinitely, like stocks, but they tend to move around a mean [6], as they are limited by economic and political factors. There is more than one definition of mean reversion, varying by model and scope. Mean reversion can be defined by historical floors and peaks or by the autocorrelation of the average return of an asset [7]. In the Vasicek model family, it is defined against the long term mean value towards which the rate is moving with a certain speed.

2.2 Neural Networks

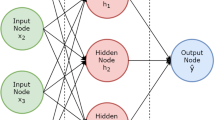
Neural networks are devised as a computational equivalent of the human brain; Every neuron is a computation node that applies a non-linear function f (e.g. sigmoid), which applies a mathematical operation on the input and the connecting weights. These nodes, like in the human brain, are interconnected. They form layers that move information forward from one layer of neurons to the next. The neurons of each layer are not connected, allowing communication only with previous and succeeding layers.

Neural networks have evolved both technically and theoretically. The latest theories that are studied propose that real life data forms lower-dimensional manifolds in its embedding space [8]. For example, a set of images of a hand-written letters that include size, rotation and other transformations can be mapped to a lower dimensional space. In this manifold, the distinct variations of the same letter are topologically close. In this context, neural networks are able to learn such manifolds from the given high dimensional datasets.

This property is largely exploited in computer vision, where transformation invariance is essential for most applications. Specific modules that are formed in this weight-learning schema, such as convolutional layers, have scaled up the performance of neural networks in problems such as tracking or image recognition. It is not unusual that handcrafted models are constantly updated or replaced by neural networks.

These qualities are also applied in financial time-series for modelling and prediction tasks [9]. Models with convolutional architectures extract temporal patterns as shapes, while models with recurrent architectures learn correlations through time points. Recurrent neural networks, extend the feed-forward paradigm allowing information to move both ways. The output of a layer is connected back to its input with the appropriate trainable weights, while feeding the results to the next layer as well.

2.3 Related Work

Currently, practitioners are calibrating the Hull-White model with a variety of methods: generic global optimizers [10], Jamshidian decomposition and swap market model approximation [11], but arguably the most popular is linear regression [12]. The simplicity of the model, together with the flexibility that can be achieved by tweaking the length of the input window, make linear regression able to approximate both the market reality and one’s expectations. The terms of the Hull-White model are reproduced by a linear model, given $t > s$:

$$\begin{aligned} r(t)=\hat{\alpha } r(s) + \hat{\theta } + \epsilon (t) \end{aligned}$$

(2)

where r(t) and r(s) are the interest for the respective time-points t, s, $\hat{\theta }, \hat{\alpha }$ the historically implied long term-mean and speed of mean-reversion, and $\epsilon$ the measured error.

The trained variables are translated back to the Hull-White parameters:

$$\begin{aligned} \begin{aligned} \hat{\alpha } = e^{-\alpha (t-s)}&\Rightarrow \alpha = \frac{- \ln \hat{\alpha }}{t-s}\\ \hat{\theta } = \frac{\theta }{\alpha } \left( 1-e^{-\alpha (t -s)} \right)&\Rightarrow \theta = \frac{\alpha \hat{\theta }}{\left( 1-e^{-\alpha (t -s)} \right) }\\ sd_{\epsilon } = \sigma \sqrt{\frac{1-e^{-2\alpha (t-s)}}{2\alpha }}&\Rightarrow \sigma = sd_{\epsilon } \sqrt{\frac{-2 \ln \hat{\alpha }}{(1-\hat{\alpha }^2)(t-s)}} \end{aligned} \end{aligned}$$

(3)

Although machine learning and neural networks have been widely used in finance for stock prediction [13], volatility modelling [14], currency exchange rate movement [15] and many more, only a few attempts have been made to address the calibration problem, and specifically, the estimation of theoretically consistent speed of mean-reversion.

Neural networks are utilized to calibrate the time-dependent mean-reversion of the Ornstein-Uhlenbeck process used for temperature derivatives in [16]. The neural network, as the approximator $\gamma$, is trained to predict the temperature of the next day. In this way, it is incorporating the dynamics of the process without explicit parameterization. Then by calculating the derivative with respect to the input of the network, they yield the value of mean-reversion. Starting from a simplified discretized version of Ornstein-Uhlenbeck process for $dt=1$, using the paper’s notation:

$$\begin{aligned} \begin{aligned} \hat{T}(t+1)&= \alpha \hat{T}(t) + e(t)\\ \hat{T}(t+1)&= \gamma (\hat{T}(t)) + e(t) \end{aligned} \end{aligned}$$

where $\hat{T}$ denotes the pre-processed temperature data at time t, $\alpha$ the simplified form of speed of mean reversion, $\sigma$ the volatility and e(t) the differential of the stochastic term¹. Then computing the derivative, we calculate the time-dependent mean reversion value:

$$\begin{aligned} \alpha (t) = \frac{d \hat{T}(t+1)}{d \hat{T}(t)} = d \gamma / d \hat{T} \end{aligned}$$

(4)

3 Mean Reversion in the Hull-White Model

We have seen that mean reversion calculation can be approached in different ways depending on the underlying model. In the Vasicek model, the mean reversion parameter is assumed to be constant for certain period of time. This assumption is lifted in more generic versions, accepting it as a function of time. Under Hull-White, when calibrating with linear regression, $\alpha$ is re-calculated periodically on historical data as the day-to-day changes are not significant for sufficiently long historical data. This approximation results in values usually within the interval (0.01–0.1) [11]. It is common among practitioners to set alpha by hand, based on their experience and current view of the market.

Consider the generic Hull-White formula:

$$\begin{aligned} dr(t)=( \theta (t) - \alpha r(t))dt + \sigma dW(t) \end{aligned}$$

(5)

Applying Ito’s lemma for some $s<t$ yields:

$$\begin{aligned} r(t) = r(s) e^{-\alpha (t -s)}+ \frac{\theta }{\alpha } \left( 1-e^{-\alpha (t -s)} \right) + \sigma e^{-\alpha (t-s)} \int _s^t e^{\alpha (t - u)} dW(u) \end{aligned}$$

(6)

The discretized form of Eq. (5) for $dt = \delta t$ is:

$$\begin{aligned} \begin{aligned} r(t+ \delta t)&\approx \theta (t) \delta t + r(t)(1- \alpha \delta t) + \sigma \epsilon (t) \end{aligned} \end{aligned}$$

(7)

where $\epsilon (t)$ denotes a value sampled from a Gaussian distribution with mean 0 and variance $\delta t$. To avoid notation abuse, this discretized approximation will be written as an equation in the following sections. Hull defined the expression for $\theta$ with constant $\alpha$ and $\sigma$ as:

$$\begin{aligned} \theta (t) = F_t(0,t) + \alpha f(0,t) + \frac{ \sigma ^2}{ \alpha } \left( 1-e^{- \alpha t)} \right) \end{aligned}$$

(8)

where $F_t(0,t)$ is the derivative with respect to time t of f(0, t), which denotes the instantaneous forward rate at maturity t as seen at time zero. Similar to [6], in our dataset the last term of the expression is fairly small and can be ignored.

4 Methodology

Our main approach for mean reversion calculation, is based on the assumption that historical rates can explain the future movement incorporating the sense of long-term or period mean value. The evolution of the yield curve is exploited in order to learn latent temporal patterns. This is achieved by training a generic function approximator that learns to predict the next-day interest rate. Starting from Hull-White model (Eq. (1)), by discretizing similar to (7) yields:

$$\begin{aligned} \begin{aligned} dr(t)&= (\theta (t) - \alpha r(t)) dt + \sigma dW(t)\\ r(t + \delta t )&= \theta (t) \delta t + r(t)( 1 - \alpha \delta t) + \sigma \epsilon (t)\\ \end{aligned} \end{aligned}$$

(9)

Let $\delta t = 1$ and $\kappa = (1- \alpha )$

$$\begin{aligned} r(t + 1) = \theta (t) + \kappa r(t) + \sigma \epsilon (t) \end{aligned}$$

(10)

We train a neural network with input r as the function approximator to learn the generalized version of (10) expressed as:

$$\begin{aligned} r(t + 1) = \gamma (r(t)) + e(t) \end{aligned}$$

(11)

where e(t) denotes the measured error. Then by calculating the derivative with respect to the input of the neural network, we can compute the values of the time function $\kappa (t)$ as:

$$\begin{aligned} \kappa (t) = \frac{d r(t+1) }{d r(t)} = \frac{d \gamma }{d r} \end{aligned}$$

(12)

Neural networks are constructed to be fully differentiable functions and their derivation is a well defined procedure, which can be found in [17].

4.1 Can Theta Be Replaced?

Notice that in Eq. (11), $\theta$ is not an input of $\gamma$, under the assumption that since the long term mean should be based on the current and historical interest rates, only them are needed as input to the network, which will infer the implied relations. In terms of [16], by not including $\theta$, the equivalent preprocessing of the data is omitted. However, under the Hull-White model long term mean relies on the forward rate which describes more complex relation between $r(t + 1)$ and r(t) that is not modeled explicitly in the network. Removing this information from the neural model makes the approximation to have a looser connection to the assumptions of the Hull-White model; in principle, it breaks the mean reverting character. To address that, we will describe two different approaches along with Eqs. (10) and (11). The first incorporates $\theta$, calculated on top of linear regression-calibrated alpha, resulting to:

$$\begin{aligned} \hat{r}(t + 1) = r(t + 1) - \theta ^{LR}(t) \end{aligned}$$

(13)

relying on a different model, such linear regression, introduces limitations and specific assumptions. This approach is not explored in the scope of this work.

As previously mentioned, the prevailing feature in the calculation of a long term mean is the forward rate. By keeping this information, the theoretical dependence of the movement of interest rate to the market expectations is partially embodied in the training data. This is realized by subtracting the first term of $\theta$, $F_t$ , to offer an approximation to long term mean value:

$$\begin{aligned} \hat{r}(t+1) = r(t + 1) - F_t \end{aligned}$$

(14)

Using Eqs. (13) and (14) the neural network is used to learn the evolution of $\hat{r}$:

$$\begin{aligned} \hat{r}(t+1) = \gamma (r(t)) +e(t) \end{aligned}$$

(15)

4.2 Mapping

In Eq. (3) mappings from linear regression parameters to Hull-White were provided. Similarly, the calculated values from neural networks need to be transformed to be usable within the interest rate model. From Eq. (12) let $\frac{d r(t+1) }{d r(t)}=\frac{d \gamma (r)}{d r} = Y(t)$. Beginning with the simple discrete form of the Hull-White model (Eq. (7)) as expressed in Eq. (12) we get:

$$\begin{aligned} \begin{aligned} Y(t)&= \kappa (t)\\ Y(t)&= 1-\alpha (t)\\ \alpha (t)&= 1 - Y(t) \end{aligned} \end{aligned}$$

(16)

The mapping in Eq. (16), is appropriate for networks accepting input only the rate of the previous time-step $\delta t = 1$. To be consistent with the assumption that multiple historical input points can battle high mean-reversion volatility, the mapping used should be suitable for functions regardless the distance of the sampled points. We move back to constant $\alpha$ and Y for simplicity, and starting with the general continuous expression of Hull-White model, we insert the simple form of Hull-White model in our derivation:

$$\begin{aligned} \begin{aligned} Y&= \frac{d \left( r(t) e^{-\alpha \delta t}+ \frac{\theta }{\alpha } \left( 1-e^{-\alpha \delta t } \right) + \sigma e^{-\alpha (t-s)} \int _s^t e^{\alpha (t - u)} dW(u) \right) }{d r(t)}\\ Y&= e^{-\alpha \delta t}\\ \alpha&= \frac{- ln( Y )}{\delta t} \end{aligned} \end{aligned}$$

(17)

The expression for $\alpha$ is the same as the one used for linear regression. The output of the networks define a partial solution for each historical time-step that is provided, i.e. the partial derivative with respect to each input, that is mapped to the time-dependent alpha function. In that sense, the output of the neural network is treated as the result of the procedure Y(t):

$$\begin{aligned} \alpha (t) = \frac{-ln( Y(t) )}{\delta t} \end{aligned}$$

(18)

Fig. 1.

Bootstrapped GBP Libor rates per maturity

4.3 Evaluation and Datasets

Three interest rate yield curve datasets were used for the experiments EUR (Fig. 2), USD (Fig. 3) and GBP (Fig. 1); The EUR dataset is comprised by 3223 data points from July 19, 2005 until November 22, 2017 with 22 maturities ranging from 1–12, 18 months, plus 2–11 years, while USD dataset starts from January 14 2002 until June 6 2011, 2446 data points with 16 maturities 1–10 and 12, 15, 20, 25, 30 and 40 years. Our datasets are fairly limited as the recorded values are daily, and in order to include all the existing rate regimes, we restricted the available maturities to 22 and 16. Our GBP data consists of 891 time-points from January 2, 2013 until June 1, 2016 with 44 maturities ranging from 0, 1, 7, 14 days, 1 to 24 months, 2 to 10 years and 12, 15, 20, 25, 30, 40, 50 years. The curve has been bootstrapped on top of OIS and only FRA and swap rates have been used.

Fig. 2.

European swap rate per maturity

Fig. 3.

USD Libor per maturity

In order to approximate the time-dependent speed of mean-reversion similarly to the linear regression method, we calculate the Pearson correlation $\in \,[-1,1]$ in a rolling window manner. This way we avoid negative alpha values which cannot be used in Hull-White model. Being limited by the extent of the datasets, the window size varies from 300, 400 to 500 time points.

5 Results

Our experiments were conducted with convolution and recurrent (LSTM) based neural networks for input length of 5, 15 and 30 data points. Throughout our tests, CNNs achieved better test-set accuracy than LSTMs in all datasets, Table 1, which is not the main interest of this work, but affects the calibration procedure overall and can play a role in deciding which is the most efficient network.

Table 1. Average prediction error

Fig. 4.

EUR Mean reversion calibrated by CNN trained with Euro data

The CNN approach (Fig. 5) seem to be in relative accordance with LR trends, following some of the patterns but not always agree on the levels of mean reversion. While there are mismatches and lags, we can spot several similarities in the movement. The evolution of alpha from CNN-5 suggests that a shorter history length results to less flexible model, at least for CNNs. Here we have three cases, with 5, 15 and 30 input length. On the lower end this behaviour is quite obvious but moving to more historical data points, the changes become stronger, resulting to higher and lower levels. In our tests, we have observed significantly different behaviours of CNNs based on the kernel_size/history_size ratio affecting the smoothness and the overall performance. The networks used here, have ratios of 2/5, 1/3 and 1/3 for CNN 5, 15 and 30 respectively.

Fig. 5.

USD Mean reversion calibrated by CNN trained with USD data

On the LSTM side, there is not a similar smoothness adjustment tool, which enables us to study the effect of history length easier. In Fig. 6 we see that shorter and longer history affect the outcome, but the relative movement is in close sync. In comparison to the CNN networks the levels are generally the same. We observe parallel evolution that is consistent in major changes, the two significant jumps are followed by all three networks. The first major difference from the evolution of LR (2012), seems as if the movement of LSTM is an exaggerated jump of the respective LR and CNN slopes parts. In the second (2014), we can see that the peak of the NNs coincide with the peak observed in LR-300 only, similar to CNN-30 but does not follow its level. For the USD dataset both CNN (Fig. 4) and LSTM (Fig. 7) preserve the same characteristics, while CNN-5 yields results closer to LSTMs, mostly because of the first part of the dataset (2004–2006), where lower alpha than LR and CNN (15 & 30) is reported. For the rest, LSTMs are closer to LR-500 but follow the same trends with CNNs.

Fig. 6.

EUR Mean reversion calibrated by LSTM trained with Euro data

Fig. 7.

USD Mean reversion calibrated by LSTM trained with USD data

In Sect. 4.1 we have discussed the role of $\theta$ in Hull-White and the significance of forward rate for its calculation. In the previous tests, the forward rate was not present in any form in the data. Following Eq. (14), we encode forward rate information by introducing the prime term of $\theta$. The CNN-30 network is trained on this data producing the results in Fig. 8. The levels of alpha are closer to LR-500 and generally undergo smoother transitions than the simply trained CNN.

Fig. 8.

CNN, LSTM, Prime calibrating GBP-Libor

Depth-wise convolution seems indeed to be suitable for parallel time-series. We observed a steady change in predictive accuracy from shorter history CNNs to longer, among the three, the network with 30-step history depth achieved the best results. However, this comparison is not simple since CNNs require certain hyper-parameter tuning, which exceeds layer count or history depth, but concerns the characteristics of the convolution layer itself; separable module, kernel size and pooling. While we focused on kernel size effects, our early tests did not favour max-pooling nor separable convolution, which led us to not further explore these options.

CNNs seem to be affected by input length and kernel size with regard to alpha calculation. 5-step networks with 2/5 kernel size ratio yield steadier results with small day-to-day changes, whereas 15 and 30 step networks generally seem to be more flexible. Particularly, CNN-15 evolution is closer to CNN-30 movement, undergoing slightly less abrupt changes. CNN-30 is the best performing network, in terms of accuracy, but also yields alpha values comparable to linear regression’s more consistently among all datasets. LSTMs did not follow exactly the same pattern in terms of predictive accuracy, all three networks, regardless the history depth, resulted in approximately the same levels.

This can be observed in alpha calculations as well, where all three networks are mutually consistent and tend to follow the same slope more closely. However, the outcome in the GBP trained networks suggests that this is the case only when they are sufficiently trained.

Using the forward prime in the training phase yields smoother results, but with level mismatches with CNN-30 and LSTM-30. Observe that, overall, all networks follow the increasing trend of linear regressions, but CNN-Prime is closer and undergoes smoother changes, while big jumps are absent (Fig. 8). This is an indication that forward rate, and market expectations as an extension, can be indeed used to extract knowledge from the market and confirms Hull’s indication to use the forward rate.

Generally, the behaviour of the networks is consistent in all datasets. We see that the reported mean reversion moves upward when IR experiences fast changes. The sensitivity to these changes varies depending on the network and especially the number of maturities observed. Studying these results, we recognize the main advantage that the inclusion of forward prime offers; it lessens the sensitivity of the network to partial curve changes, augmenting the importance of the curve as a whole. Even if the evaluation of these results cannot be exact, the CNN networks seem to have greater potential and proved more suitable for prediction and mean reversion calculation. However, in real life conditions the use of a smoothing factor and the inclusion of prime are deemed necessary. LSTMs may require more data for training, but produce consistent results regardless of the number of historical data points supplied. These findings suggest that history depth can play greater role in the performance of CNN networks than LSTM.

6 Conclusion

We presented a method to calibrate the speed of the mean reversion in the Hull-White model using neural networks, based only on historical interest rate data. Our results demonstrate the suitability of depth-wise convolution and provide evidence for the advantages of neural network approach over existing methodologies. The obtained mean reversion is comparable to rolling-window linear regression’s results, allowing for greater flexibility while being less sensitive to market turbulence.

In the future, we would like investigate the comparison with more advanced econometric methods than linear regression, e.g. Kalman filters [18]. Another interesting direction is the understanding of learning with neural networks. Sound model governance and model risk management frameworks are essential for financial institutions in order to comply with regulatory requirements. This creates a constrained environment for the growth of black box methods such as neural networks. Nevertheless, the latest trends in machine learning reveal that the research in the direction of opening the black box is growing [19].