CARN: Convolutional Anchored Regression Network for Fast and Accurate Single Image Super-Resolution

Abstract

Although the accuracy of super-resolution (SR) methods based on convolutional neural networks (CNN) soars high, the complexity and computation also explode with the increased depth and width of the network. Thus, we propose the convolutional anchored regression network (CARN) for fast and accurate single image super-resolution (SISR). Inspired by locally linear regression methods (A+ and ARN), the new architecture consists of regression blocks that map input features from one feature space to another. Different from A+ and ARN, CARN is no longer relying on or limited by hand-crafted features. Instead, it is an end-to-end design where all the operations are converted to convolutions so that the key concepts, i.e., features, anchors, and regressors, are learned jointly. The experiments show that CARN achieves the best speed and accuracy trade-off among the SR methods. The code is available at https://github.com/ofsoundof/CARN.

Keywords

1 Introduction

Super-resolution (SR) refers to the recovery of high-resolution (HR) images containing high-frequency detail information from low-resolution (LR) images [9, 10, 27]. Due to the rapid thriving of machine learning techniques, the main direction of SR research has shifted from traditional reconstruction-based methods to example-based methods [6, 20, 21, 35]. Nowadays, deep learning has shown its promising prospect with successful applications in multiple computer vision tasks such as image classification and segmentation, object detection and localization [11, 15, 24, 30]. Specifically, the convolutional neural network (CNN) mimics the process of how human beings perceive visual information. And by stacking a number of convolutional layers, the network tries to extract high-dimensional representation of raw natural images which in turn helps the network to understand the raw images.

Fig. 1.

Avg. PSNR vs. runtime trade-off on Set5 ($\times 4$) tested on Intel Core i7-6700K 4GHz CPU. DIV2K dataset [2] is used to train the network. Our proposed has the best speed and accuracy trade-off capability. Details in Sect. 4.

During the past years, single image super-resolution (SISR) algorithms developed steadily in parallel with the advances in deep learning and continuously improved the state-of-the-art performances [2, 33]. Super-resolution convolutional neural network (SRCNN) [6] with its three functional layers is the first CNN to achieve state-of-the-art performance on SISR. However, due to the limitation of traditional stochastic gradient descent (SGD) algorithm, the training of SRCNN took such a long time that the network with more layers seemed to be untrainable. Very deep SR (VDSR) addressed the problem of training deeper SR networks by different techniques including residual learning and adjustable gradient clipping [21]. The VDSR network contains 20 CNN layers and converges quite fast in comparison with SRCNN. SRResNet [26] gained insights from residual network [15] and was built on residual blocks between which skip connections were also added to constrain the intermediate results of residual blocks.

The performance of the SR methods is measured mainly in terms of speed and accuracy. As the CNN goes deeper and more complex, the accuracy of SR algorithm improves at the expense of speed [28]. The earlier works operated on HR grid, i.e., bicubic interpolation of the LR image, which provided no extra information but impeded the execution of the network. Thus, FSRCNN [8] was proposed to operate directly on the LR images, which boosted the inference speed. In addition, the large receptive field ($9 \times 9$) of SRCNN [6] that occupied the major computation was replaced by a $5 \times 5$ filter followed by 4 thin CNN layers. ESPCN [32] was also introduced which works on the LR images with a final efficient sub-pixel convolutional layer. The idea is to derive a final feature map with output dimension $C (color channel) \times r (upscaling factor) \times r$ from the last convolutional layer and use a pixel-shuffler to generate the output HR image.

The new developments in both speed and accuracy directions show their contradictory nature. In Fig. 1 is depicted the runtime versus PSNR accuracy for several representative state-of-the-art methods. Higher accuracy usually means deeper networks and higher computation. Improving on both directions requires designing more efficient architectures. Thus, instead of regarding CNN as a black box, more insights should be obtained by analyzing classical algorithms.

We start with A+ [35] which achieves top performance in both speed and accuracy among traditional example-based methods. A+ casts SR into a locally linear regression problem by partitioning the feature space and associates each partition with an anchor. Since A+ assigns each feature to a unique anchor, it is not differentiable w.r.t. anchors, which prevents end-to-end learning. To solve this limitation, anchored regression network (ARN) [3] proposes the soft assignment of features to anchors whose importance is adjusted by the similarity between the features and anchors. However, since ARN is introduced as a powerful non-linear layer which, for SR, requires as input hand-crafted and patch-based features and needs some preprocessing and post-precessing operations, it is not a fully-fledged end-to-end trainable CNN.

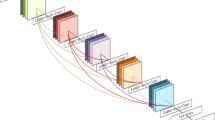
In this paper, we propose the convolutional anchored regression network (CARN) (see Fig. 3) which has the capability to efficiently trade-off between speed and accuracy, as our experiments will show. Inspired by A+ [34, 35] and ARN [3], CARN is formulated as a regression problem. The features are extracted from input raw images by convolutional layers. The regressors map features from low dimension to high dimension. Every regressor is uniquely associated with an anchor point so that by taking into account the similarity between the anchors and the extracted features, we can assemble the different regression results to form output features or the final image. In order to overcome the limitations of patch-based SR, all of the regressions and similarity comparisons between anchors and features are implemented by convolutional layers and encapsulated by a regression block. Furthermore, by stacking the regression block, the performance of the network increases steadily.

We validate our CARN architecture (see Fig. 3) for SR on 4 standard benchmarks in comparison with several state-of-the-art SISR methods. As shown in Fig. 1 and in the experimental Sect. 4, CARN is capable to trade-off the best between speed and accuracy, filling in the efficiency gap.

Thus, the main two contributions of this paper are:

• First, we propose the convolutional anchored regression network (CARN), a fully fledged CNN that enables end-to-end learning. All of the features, regressors, and anchors are learned jointly.

• Second, the proposed CARN achieves the best trade-off operating points between speed and accuracy. CARN is much faster than the accurate SR methods for comparable accuracy and more accurate than the fast SR methods for comparable speed.

The rest of the paper is organized as follows. Section 2 reviews the related works. Section 3 introduces CARN from the perspective of locally linear regression and explains how to convert the operations to convolution. Section 4 shows the experimental results. Section 5 concludes the paper.

2 Related Works

Neighborhood embedding is one of the early example-based SISR method which assumes LR and HR image patches live in a manifold and approximates HR image patches with linear combination of their neighbors using weights learned from the corresponding LR embeddings [5]. Instead of operating directly on image patches, sparse coding learns a compact representation of the patch space, resulting a codebook of dictionary atoms [20, 38, 39]. By constraining patch regression problem with $\ell _2$ regularization, anchored neighborhood regression (ANR) gives a closed-form representation of an anchor atom with respect to its neighborhood atoms [34]. Then the inference process for each input patch becomes a nearest neighbor search followed by a projection operation. A+ [35] extends the representation basis from dictionary atoms to features in the training images. However, the limitation of these works is that they work on hand-crafted features.

Since SRCNN [6, 7], the research community has transferred and delved into the utilization of deep features. Gu et al. [13] presented a convolutional sparse coding (CSC) based SR (CSC-SR) to address the consistency issue usually ignored by the conventional sparse coding methods. Kim et al. [21] proposed VDSR and validated the huge advantage of deep CNN features to tackle the ill-posed problem. They also proposed a deeply-recursive convolutional network (DRCN) [22] using recursive supervision and skip connections. To design new architecture, researchers absorbed knowledge from the advances in deep learning techniques. Ledig et al. used generative adversarial networks (GAN) [12] and residual networks [15] to build their photo-realistic SRGAN and highly accurate SRResNet. Lai et al. [25] incorporated pyramids in their design to enlarge LR images progressively so that the sub-band residuals of HR images were recovered. Some others [36, 40] resorted to DenseNet [16] connections or the combinations of residual net and DenseNet.

3 Convolutional Anchored Regression Network (CARN)

In this section, we start with the basic assumption of locally linear regression, derive the insights from it, and point out how we convert the architecture to convolutional layers in our proposed convolutional anchored regression network (CARN).

3.1 Basic Formulation

Assume that a set of k training examples are represented by $\{(\mathbf {x}_1,\mathbf {y}_1),...,(\mathbf {x}_{k},\mathbf {y}_{k})\}$, where the features $\mathbf {x}_i\in \mathbb {R}^d$ can be hand-crafted in locally linear regression setup or extracted by some layer in CNN, and the label $\mathbf {y}_i\in \mathbb {R}^{d'}$ is real-valued and multidimensional. Then the aim is to learn a mapping $g: \mathbb {R}^d \rightarrow \mathbb {R}^{d'}$ which approximates the relationship between $\mathbf {x}_i$ and $\mathbf {y}_i$.

The basic assumption of locally linear regression is that the relationship between $\mathbf {x}_i$ and $\mathbf {y}_i$ can be approximate by a linear mapping within disjoint subsets of the feature space. That is, there exists a partition of the space $U_1,\cdots ,U_m \subset \mathbb {R}^d$ satisfying disjoint and unity constrains $\bigcup _{i=1}^m U_i = \mathbb {R}^d$ and $U_i\cap U_j = \emptyset$ if $i\ne j$, and m associated linear regressors $(\mathbf {W}_1,b_1),\cdots ,(\mathbf {W}_m,b_m)$ such that for $\mathbf {x}_i\in U_j$:

$$\begin{aligned} \mathbf {y}_i \approx \mathbf {W}_j \mathbf {x}_i + b_j, \end{aligned}$$

(1)

where $\mathbf {W}_j \in \mathbb {R}^{d' \times d}$. Since linearity is only constrained on a local subset, the mapping g is globally nonlinear. Then the problem becomes how to find a proper partition of the feature space and learn regressors that make the best approximation.

Timofte et al. [34, 35] proposed to associate each subset $U_i$ with an anchor point. The space is partitioned according to the similarity between the anchor points and the features, namely,

$$\begin{aligned} U_i = \{ \mathbf {x} \in \mathbb {R}^d|\forall j \ne i, s(\mathbf {x}, \mathbf {a}_i) >s(\mathbf {x}, \mathbf {a}_j)\}, \end{aligned}$$

(2)

where $\mathbf {a}_i \in {A}$ is the anchor point, s is the similarity measure and can be Euclidean distance or inner product [35].

Since the features are assigned to uniques anchors with the maximum similarity measure, this partition is not differentiable with respect to the anchors. This impedes the incorporation of SGD optimization. Thus, Agustsson et al. [3] proposed to assign features to all anchors whose importance was represented by the similarity measure, namely,

$$\begin{aligned} \varvec{\alpha }(\mathbf {x}) = \sigma \left( \left( s(\mathbf {x}, \mathbf {a}_1), \cdots , s(\mathbf {x}, \mathbf {a}_m) \right) ^T\right) , \end{aligned}$$

(3)

where $\sigma (\cdot )$ is softmax function

$$\begin{aligned} \sigma (\mathbf {z})_i = \frac{\exp (z_i)}{\sum _{j=1}^{m}\exp (z_j)}, i = 1, \cdots , m. \end{aligned}$$

(4)

Then the contribution of every regressor is considered by taking a weighted average of their regression result with respect to the $\mathbf {\alpha }$ coefficients, namely,

$$\begin{aligned} \tilde{f}(\mathbf {x}) = \sum _{i=1}^{m}\alpha (\mathbf {x})_i(\mathbf {W}_i\mathbf {x}+b_i) \end{aligned}$$

(5)

Fig. 2.

CARN Regression Block. The upper branch learns the mapping from one dimension to another and the weights in the conv layer are referred to as regresors. The lower branch generate coefficients to weigh the regression results of the upper branch. The weights of the conv layer in the lower branch are referred to as anchors.

3.2 Converting to Convolutional Layers

We build the convolutional regression block based on the above analysis. This regression block can be used as an output layer to form the final SR image or as a building block to form a deep regression network. A reference to Figs. 2 and 3 leads to a better understanding of the building process.

In Subsect. 3.1, we assume that vectors are mapped from $\mathbb {R}^d$ to $\mathbb {R}^{d'}$. In this subsection, the vectors $\mathbf {x}$ and $\mathbf {y}$ correspond to multi-dimensional features extracted from feature maps of convolutional layers. Regression based SR (A+ and ARN) extracts $\mathbf {x}$ with a certain stride from the feature map and the algorithm operates on the extracted patches. For ARN, every regressor computes regression results for all of the patches. If the extraction stride in ARN is 1, then role of the ARN regressor is actually the same with the kernel in conv layers with stride 1. Thus, in order to relate to convolution operations, we can suppose $\mathbf {x}$ be a vector corresponding to an extracted feature with dimension $d=c \times w \times h$ from the feature map of a convolutional layer, where w and h are the width and height of the extracted features and c is the number of channels of input feature map. The dimension of the feature map is denoted as $\mathcal {W} \times \mathcal {H}$. The regressor $\mathbf {W}_i$ can be rewritten as a row vector, namely,

$$\begin{aligned} \mathbf {W}_i =\begin{bmatrix} \varvec{\omega }_{i1}^T \\ \vdots \\ \varvec{\omega }_{id'}^T \end{bmatrix} =\begin{bmatrix} \varvec{\omega }_{i1}&\cdots&\varvec{\omega }_{id'} \end{bmatrix}^T, \end{aligned}$$

(6)

where $\varvec{\omega }_{ij}^T, j=1, \cdots , d'$ is the row vector of $\mathbf {W}_i$ with dimension $d=c \times w \times h$. Assuming that the the features are collected by shifting the window pixel by pixel, then by transforming the vector $\varvec{\omega }_{ij}^T$ to a 3D tensor, it can be implemented via a convolution operation with c input channels and kernel size $w \times h$. In most cases, square kernels are used, namely, $w = h$. Since $\mathbf {W}_i$ has $d'$ rows and each of them is converted to a convolution, $\mathbf {W}_i$ can be implemented as a single convolution with $d'$ outputs. In our design, $d'$ could equal $r \times r$ denoting upscaling factor when the regression block is used as an output layer or c denoting inner channel that maintains learned representation when used as a building block. Considering that there are m regressors and each of them corresponds to a convolution which operates on the same input feature map, the ensemble of regressors $\bar{\mathbf {W}} = \begin{bmatrix} \mathbf {W}_{i}&\cdots&\mathbf {W}_{m} \end{bmatrix}$ can be implemented by a convolutional layer with kernel size $w \times h$ and output channel $m\cdot d'$, namely,

$$\begin{aligned} \mathbf {{R}} \in \mathbb {R}^{\mathcal {W} \times \mathcal {H} \times m\cdot d'} = \mathbf {{W}} \circledast \mathbf {{X}} + \mathbf {{B}}, \end{aligned}$$

(7)

where $\circledast$ denotes convolution, $\mathbf {{X}} \in \mathbb {R}^{\mathcal {W} \times \mathcal {H} \times c}$ the feature map where $\mathbf {x}$ is extracted, $\mathbf {{W}} \in \mathbb {R}^{c \times w \times h \times m\cdot d'}$ the weights of the convolution, and $\mathbf {{B}} \in \mathbb {R}^{m\cdot d'}$ the biases. As stated above, we use $\mathcal {W} \times \mathcal {H}$ to denote the dimension of the feature map. Note that the kernel $\mathbf {W}$ is a 4D tensor with dimension ${c \times w \times h \times m\cdot d'}$. The $4^{th}$ dimension has size $m\cdot d'$ which denotes one single value.

Similarly, if inner product is taken as the similarity measure, then it can also be implemented as a convolution. The anchor points $\mathbf {a}_i$ have the same dimension with features $\mathbf {x}$ and can act as the kernel of the convolution. By aggregating the operations in (3), the soft assignment of features becomes a convolutional layer with a kernel size $w\times h$ and m output channels, namely,

$$\begin{aligned} \mathbf {{C}} \in \mathbb {R}^{\mathcal {W} \times \mathcal {H} \times m}= \sigma (\mathbf {{A}} \circledast \mathbf {{X}}), \end{aligned}$$

(8)

where $\mathbf {{A}} \in \mathbb {R}^{c \times w \times h \times m}$ is the weights gathered from the m anchors $\mathbf {a}_1,\cdots ,\mathbf {a}_m$, $\sigma$ is softmax activation function. In order to aggregate the convolution (regression) result and achieve the functionality of (5), the regression result $\mathbf {{R}}$ and similarity measure $\mathbf {{C}}$ are reshaped to 4D tensors, multiplied element-wise, and summed along the anchor dimension, resulting a 3D tensor, namely,

$$\begin{aligned} \mathbf {{Z}} \in \mathbb {R}^{\mathcal {W} \times \mathcal {H} \times d'} = \mathcal {S}_3(\mathcal {R}(\mathbf {{C}}) \otimes \mathcal {R}(\mathbf {{R}})), \end{aligned}$$

(9)

where the operator $\mathcal {R}$ reshapes $\mathbf {{C}}$ and $\mathbf {{R}}$ to $\mathcal {W} \times \mathcal {H} \times m \times d'$ and $\mathcal {W} \times \mathcal {H} \times m \times 1$ tensors, $\otimes$ is element-wise multiplication where broadcasting is used along the fourth dimension, the operator $\mathcal {S}_3$ sums along the third (anchor) dimension. When used as an output layer, the following pixel-shuffler or Tensorflow depth-to-space operator transforms $\mathbf {{Z}}$ to an SR image $\tilde{\mathbf {Z}}$ with dimension $r\mathcal {W} \times r\mathcal {H}$.

Fig. 3.

CARN architecture: 3 convolutional layers extract features from LR input image and a stack of regression blocks maps to HR space. The number of filters (f) of convolutional layers is shown in the square brackets. All filters have kernel size $3\times 3$ and stride 1. More details in Sect. 3.

3.3 Proposed CARN Architecture

The architecture of CARN is shown in Fig. 3. The first three convolutional layers extract features from the LR images followed by a stack of regression blocks. The last regression block acts as a upsampling block while the other regression blocks’ input and output has the same number of feature maps. In order to ease the training of the regression blocks, skip connections are added between them. An exception is made for the last regression block that acts as an output layer. If the number of inner channels c and $r\times r$ equals, then a skip connection is also added for the last regression block. Otherwise, there is no skip connection for it.

The regression block shown in Fig. 2 is built according to (7), (8), and (9). The upper and lower branches achieve the functionality of regression and measuring similarity, respectively. Then the element-wise multiplication and reduced sum along the anchor dimension assemble the results from different regressors. We refer to the weights in the uppper and lower branch as regressors and anchors, respectively. The numbers of regressors and anchors are the same and denoted as m. The number of inner channels is denoted as $d'$ which is equal to the number of channels of the output feature map of the regression block. In A+, the anchors are the atoms of a learned dictionary that is a compact representation of the image feature space while in CARN the anchors, regressors, and features are learned jointly.

4 Experiments

In this section, we compare the proposed method with state-of-the-art SR algorithms. We firstly introduce experimental settings and then compare the SR performance and speed of different algorithms.

4.1 Datasets

DIV2K dataset [2] is a newly released dataset in very high resolution (2K). It contains 800 training images, 100 validation images, and 100 test images. We use the 800 training images to train our network. The training images are cropped to sub-images with size 64 for $\times 2$ and $\times 4$, and 66 for $\times 3$. There is no overlap between the sub-images. Data augmentation (flip) is used for the training. We test the networks on the commonly used datasets: Set5 [4], Set14 [38], B100 [29], and Urban100 [17]. We follow the classical experimental setting adopted by most of previous methods [17, 21, 34, 35]. The LR image is generated by the Matlab bicubic downscale operation, and we only compute the PSNR and SSIM scores on the luma Y channel of the super-resolved image for most of the experiments. For the challenge, the network operates on a RGB image and output a RGB image. In that case, the PSNR and SSIM are also computed on the RGB channel.

4.2 Implementation Details

The number of inner channels are set as 16 for upscaling factor $\times 2$ and $\times 4$, and 18 for $\times 3$ unless otherwise stated. Three feature layers are used. Since c equals to $r \times r$ for $\times 4$, skip connection is added for the last regression block. We always use 16 anchors/regressors for our experiments unless otherwise stated.

We use residual learning that only recovers the difference between the HR image and bicubic interpolation. We train our network using mean square error (MSE) with weight decay 0.0001. We used the weight initialization method proposed by He et al. [15]. The batch size is 64. Adam optimizer [23] is used to train the network. The learning rate is initialized to 0.001 and decreased by a factor of 10 for every $2 \times 10^5$ iterations. We train the network for $5 \times 10^5$ iterations. So there are 2 decreases of the learning rate.

We implement our network with Tensorflow [1] and use the same framework to modify other methods (like ESPCN [32] and SRResNet [26]). We also reimplement SRCNN, ESPCN, VDSR, SRResNet, FSRCNN with Tensorflow according to the original paper. When comparing these methods, bicubic interpolation is not included. The codes of these methods only differ in the architecture design. All the other codes including the training and testing procedure are the same so that the comparison is fair. We report the GPU and CPU runtime based on our implementation and copy the PSNR and SSIM values from the corresponding original paper. The speed is reported for a single Intel Core i7-6700K 4.00GHz CPU for most of the experiments and also reported for Titan Xp GPU (Table 1). Our networks were trained on a server with Titan Xp GPUs.

The PIRM 2018 Challenge. We participated in the PIRM 2018 SR challenge of Perceptual Image Enhancement on Smartphones [19]. The challenge only focuses on $\times 4$ upscaling. The input images of the challenge are bicubically interpolated RGB images while our default setting is LR luminance image. Thus, the above described network configuration of CARN is changed somehow to adapt to the challenge. First of all, the number of feature layers is reduced to 2 and the stride is set to 2. So after the two layers, the features are in low resolution. In addition, eight anchors/regressors are used for the network trained for the challenge while the number of inner channels is kept as 16. Upsampling is done by the last regression block and the Tensorflow depth-to-space operation. Since it’s required to recover the whole RGB image, the number of output feature maps of the last regression block is $4 \times 4 \times 3$. The modifications such as reducing the number of features layers and anchors/regressors are made in order to make the network faster. We used 3, 5, and 7 regression blocks in the challenge and the corresponding trained models were submitted.

4.3 Parameters vs. Performance

In Table 2, we make a summary of PSNR vs. runtime comparison of CARN with different setting for upscaling factor $\times 3$ on Set5 and Set14. Increasing the value of any of the three hyper parameters, i.e., number of regression blocks, number of inner channels, and number of anchors/regressors, separately, PSNR improvements are achievable at the expense of computational complexity/runtime. By comparing $C_4$(3,72,16) with $C_3$(3,36,16), we find that the runtime triples while the PSNR performance is comparable. While $C_4$(3,72,16), $C_3$(3,36,16) and $C_8$(3,36,32) have comparable number of parameters, $C_8$(3,36,32) achieves the best trade-off between PSNR and runtime. This fact enlightens us to make a balanced selection for CARN between the number of inner channels and regressors constrained by limited resources. Note that $C_9$(1,9,16) has only one regression block and its runtime is already very close to ESPCN while being 0.42 dB better in PSNR terms.

Table 1. $\times 4$ comparison of number of parameters, memory consumption, GPU runtime, CPU runtime, and PSNR between different network architectures. Memory consumption is measured by Tensorflow when generating the HR version of baby image in Set5 on a GPU. The other metrics (GPU & CPU runtime, PSNR) are averaged on Set5 dataset.

Table 2. Average PSNR (dB) vs. runtime (s) of CARN under configurations (C) with different numbers of regression blocks (n), inner channels (c), and regressors (m) for upscaling factor 3.

4.4 Compared Methods

We compare the proposed method CARN at different operating points (depth) with several other methods including SRCNN [7], FSRCNN [8], A+ [35], ARN [3], ESPCN [32], VDSR [21], RAISR [31], IDN [18], and SRResNet [26] in terms of PSNR, SSIM [37], and runtime. We resort to the benchmark set by Huang et al. [17] which provides the results of several methods.

SRResNet is among the most accurate state-of-the-art methods with reasonably low runtime while ESPCN is among the fastest SR methods with a good accuracy. Therefore, we derived additional variants for the abovementioned methods to investigate the trade-off capability of their designs. We have implemented our SRResNet [26] variants with fewer residual blocks (2, 4, 8, 12) than the original (16 residual blocks) to achieve different operating points trading accuracy for speed and trained them using DIV2K train data as for our CARN. We also, push the performance limits for ESPCN [32] and implemented our own variants by increasing the number of convolutional layers from 3 (original setting) to 7, 11, and 20, respectively.

Table 3. Average PSNR/SSIM/runtime for upscaling factor (S) 2, 3 and 4 on datasets Set5, Set14, B100 and Urban100 for different methods.

4.5 Results

Quantitative Results. The PSNR and SSIM results and runtimes of several compared methods including our CARN on the 4 datasets are summarized in Table 3. For CARN, the default number of regression blocks is set to 7 (CARN7), but we report results also for a single regression block (CARN1). Based on the results, we make a couple of observations. CARN outperforms VDSR in both PSNR and runtime by large margins, which validates the efficiency of the proposed method. CARN is much faster than SRResNet even when SRResNet uses only 2 residual blocks, but CARN is less accurate than SRResNet with 16 residual blocks. CARN is dramatically improving in accuracy over the fast SR methods such as RAISR, FSRCNN and ESPCN. CARN is capable to trade off accuracy for speed and to compete to these methods on speed while keeping an accuracy advantage. Note that ESPCN while fast saturates rapidly above 11 convolutional layers and with 20 convolutional layers achieves worse speed and accuracy than our CARN with 3 regression blocks. While both ARN [3] and CARN use the same number of regression layers and anchors, our CARN outperforms ARN by a large margin for $\times 3$ (1 dB PSNR on Set5, 0.56 dB on Set14, and 0.48 dB on B100).

Fig. 4.

SR results of face image by different methods for upscaling factor 4.

Fig. 5.

SR results of baby image by different methods for upscaling factor 4.

Fig. 6.

SR results of zebra image by different methods for upscaling factor 4.

Visual Results. For visual assessment of the performance we pick the face, baby, and zebra images and show in Figs. 4, 5, and 6, respectively, the super-resolved results obtained by a couple of methods in comparison with our CARN. For each we report also the PSNR and SSIM scores and the runtime. We note that our CARN super-resolved images exhibit a fair amount of artifacts, but fewer than in the compared image results, and have better PSNR and SSIM scores.

Parameter and Memory. In Table 1, we report the number of parameters and the memory requirements measured by Tensorflow for different algorithms. Compared with VDSR and SRResNet16, CARN reduced the number of parameters by several times. Excepting the extremely simple FSRCNN and ESPCN, the memory requirements of all the other algorithms are at the same level (10 GB) although VDSR requires slightly more memory. The reason may be that the Tensorflow tends to allocate as much as GPU memory as it can get.

Efficiency: Speed vs. Runtime. In Fig. 1, we compare the proposed method with several state-of-the-art efficient SISR methods in term of PSNR vs. runtime trade-off. SRResNet [26] with different numbers of residual blocks (2, 4, 8, 12, 16) achieves top PSNR accuracy but is much slower than other runtime efficient methods (CARN, FSRCNN [8], ESPCN [32]). Despite being quite fast, FSRCNN is at a low accuracy level. For ESPCN, the accuracy of the network stagnates quickly with the increasing number of layers (20 layers of the last point on the ESPCN curve). The proposed CARN with 7 regression blocks (CARN7) achieves $\sim$31.8 dB PSNR within 0.1s runtime. CARN7 is over 22 times faster than VDSR [21] for a better accuracy. By contrast, a concurrent work, the information distillation network (IDN) [18] is only 6 times faster than VDSR on Set5 ($\times 4$) while our method achieves comparable accuracy on Set14 [38], B100 [29], and higher accuracy on Urban100 [17] in terms of PSNR (See Table 3) [18]. We also notice the very recent state-of-the-art Deep Back-Projection Networks (DBPN) work [14]. However, DBPN is not runtime efficient; as reported in [33], on a GPU, it takes seconds to 8$\times$ super-resolve an LR input DIV2K image.

In Table 1, we also report the GPU runtime of different algorithms, which tell the same story. It takes tens of milliseconds on GPU for SRResNet and VDSR to recover the images while ESPCN stagnates with increased number of layers. In conclusion, this table shows that CARN achieves the best PSNR vs. runtime tradeoff. The runtime gain of CARN7 is partly due to the reductions of number of parameters (compared with SRResNet and VDSR in Table 1). Another reason is that CARN operates on low resolution images (compared with SRCNN and VDSR).

Among the compared methods including ESPCN and SRResNet and the derived variants, CARN clearly trades off better the runtime for accuracy and fills in the gap between fast SR methods (RAISR, FSRCNN, ESPCN) and accurate SR methods (SRResNet, VDSR).

Although EDSR [28] outperforms in accuracy all of the efficient SISR methods, it is much slower than VDSR [21], and orders of magnitude slower than our CARN approach.

5 Conclusion

In this paper, we introduced the convolutional anchored regression network (CARN), a novel deep convolutional architecture for single image super-resolution. This network was inspired by the conventional locally linear regression methods A+ and ARN. The regression block was derived by analyzing the operations in A+. The regression and similarity comparison operations were converted to convolutions, which in combination with the feature layers made the network a fully fledged end-to-end learnable CNN. The proposed method is very efficient and capable to achieve the best trade-off between speed and accuracy among the compared SISR methods.