Mining Tree Patterns with Partially Injective Homomorphisms

Abstract

One of the main differences between inductive logic programming (ILP) and graph mining lies in the pattern matching operator applied: While it is mainly defined by relational homomorphism (i.e., subsumption) in ILP, subgraph isomorphism is the most common pattern matching operator in graph mining. Using the fact that subgraph isomorphisms are injective homomorphisms, we bridge the gap between ILP and graph mining by considering a natural transition from homomorphisms to subgraph isomorphisms that is defined by partially injective homomorphisms, i.e., which require injectivity only for subsets of the vertex pairs in the pattern. Utilizing positive complexity results on deciding homomorphisms from bounded tree-width graphs, we present an algorithm mining frequent trees from arbitrary graphs w.r.t. partially injective homomorphisms. Our experimental results show that the predictive performance of the patterns obtained is comparable to that of ordinary frequent subgraphs. Thus, by preserving much from the advantageous properties of homomorphisms and subgraph isomorphisms, our approach provides a trade-off between efficiency and predictive power.

1 Introduction

Despite the facts that graphs can be considered as relational structures and graph patterns as function-free first-order goal clauses, inductive logic programming (ILP) [9] and graph mining are typically regarded as independent research fields. One of the reasons for this separation lies in the relative simplicity of the vocabularies for graphs as relational structures. Another important difference is that while the pattern matching operator in ILP is defined by subsumption (cf. [9]), a weakening of first-order implication, it is mainly the subgraph isomorphism in graph mining. For first-order function-free clauses, subsumptions are in fact homomorphisms between relational structures (see, e.g., [7]). Thus, ILP (mainly) applies relational homomorphisms, while graph mining deploys subgraph isomorphisms.

Our goal is to propose a binary feature space for predictive graph mining that is spanned by frequent patterns. On the one hand, frequent patterns w.r.t. homomorphism result, due to the lack of injectivity, in a loss in predictive performance compared to subgraph isomorphism when used for classification tasks. On the other hand, however, homomorphism is decidable in polynomial time for a broad class of patterns for which subgraph isomorphism remains persistently NP-complete (e.g., while the existence of a homomorphism from a path into a graph can be decided in polynomial time, this problem is NP-complete for subgraph isomorphism). As a trade-off between expressiveness and complexity, our goal is to preserve from the rigidity of subgraph isomorphism as much as possible, while utilizing the efficiency of homomorphisms for tractable graph classes. The difference between these two pattern matching operators is that any subgraph isomorphism is in fact an injective homomorphism. We therefore consider a natural transition from homomorphisms to subgraph isomorphisms that is defined by partially injective homomorphisms, i.e., which require injectivity only for a subset of the vertex pairs.

For loop-free graphs, any partially injective homomorphism can polynomially be reduced to an ordinary homomorphism by extending the graphs with additional edges corresponding to the injectivity constraints. To distinguish between original and constraint edges, we use edge colors. It holds that distinct sets of injectivity constraints define different partially injective homomorphisms problems between the same pattern and target graphs. In particular, the empty (resp. maximum) set of injectivity constraints corresponds to ordinary homomorphism (resp. subgraph isomorphism). By means of partially injective homomorphisms we can thus relax the rigid conception of having the binary choice between homomorphism and subgraph isomorphism, and are flexible to dynamically choose the degree of injectivity in the pattern matching operator. To the best of our knowledge, the application of dynamic pattern matching operators is an entirely novel characteristic in pattern mining, distinguishing it from all other traditional pattern matching operators used in ILP and graph mining.

Our approach can efficiently be applied to all pattern classes from which homomorphisms can be decided efficiently. For this work we consider the class of bounded tree-width graphs [11] (cf. [3] for the positive result on the complexity of homomorphisms from bounded tree-width graphs). More precisely, we restrict the patterns to trees and require the tree together with the additional constraint edges to form a graph of tree-width at most k, where $k>0$ is some (small) constant. While this kind of partially injective homomorphisms from trees into arbitrary graphs is decidable in polynomial time, ordinary subgraph isomorphism from a tree remains NP-complete.

Using this idea, we propose an algorithm mining frequent trees w.r.t. partially injective homomorphisms. The rationale behind the choice of tree patterns is that the predictive performance achieved with frequent trees compares well to that of frequent connected subgraphs [13]. As the set of injectivity constraints depends on the particular pattern at hand, the output of the mining algorithm contains not only the tree patterns, but also the injectivity constraints. A complete enumeration of all frequent patterns is, however, practically infeasible for the potentially huge number of injectivity constraint sets. We overcome this problem by considering only patterns which are k-trees [12], i.e., edge maximal graphs of tree-width at most k. Utilizing the algorithmic definition of k-trees (cf. [12]), we arrive at a natural refinement operator for the corresponding pattern mining problem, allowing for an efficient frequent pattern enumeration.

We have empirically evaluated the predictive performance and the runtime of our approach on real-world and artificial datasets. The predictive performance obtained by frequent subtrees w.r.t. partially injective homomorphism was very close to that of ordinary frequent subtrees and hence, to that of ordinary frequent subgraphs [13], and was achieved already for tree-width at most 3. Regarding the runtime, our algorithm is slower on molecular graphs than GASTON [10] and FSG [4] which seem to be specifically designed for this kind of graphs. However, already on slightly more complex structures beyond chemical graphs, our method always terminates and is faster by at least 1 (up to 3) orders of magnitude than GASTON and FSG (when they terminate at all). Thus, our approach offers a trade-off between runtime and predictive power via the choice of tree-width.

The rest of the paper is organized as follows. We collect the necessary notions in Sect. 2, introduce the concept of partially injective homomorphisms in Sect. 3, and present our mining algorithm in Sect. 4. We report our empirical results in Sect. 5 and conclude in Sect. 6. For page limitations, proofs are omitted in this short version.

2 Notions and Notation

In this section we collect the necessary notions from graph theory (see, e.g., [5]) and fix the notation. For a set S, let $[S]^2 = \{ X \subseteq S: |X| = 2\}$. The set $\{u,v\} \in [S]^2$ is denoted by uv. An undirected (resp. directed) labeled graph over an alphabet $\varSigma$ is a triple $G=(V, E, \ell )$ consisting of a set V of vertices, a set $E \subseteq [V]^2$ (resp. $E \subseteq V \times V$) of edges, and a labeling function $\ell : V \cup E \rightarrow \varSigma$ assigning a label from $\varSigma$ to each vertex and edge. We often denote the set of vertices of G by V(G) and the set of edges by E(G). For simplicity we present our result for undirected graphs, by noting that any undirected graph G can be regarded as a directed graph such that all edges $uv \in E(G)$ are replaced by the directed edges (u, v) and (v, u). Accordingly, unless otherwise stated, by graphs we always mean undirected graphs.

A homomorphism from a graph $G=(V,E,\ell )$ into a graph $G'=(V',E',\ell ')$ is a function $\varphi : V \rightarrow V'$ preserving all edges and labels, i.e., (i) $\varphi (u)\varphi (v) \in E'$ for all $uv \in E$, (ii) $\ell (v)=\ell '(\varphi (v))$ for all $v \in V$, and (iii) $\ell (uv)=\ell '(\varphi (u)\varphi (v))$ for all $uv \in E$. If, in addition, $\varphi$ is injective then it is a subgraph isomorphism from G to $G'$. The graphs G and $G'$ above are isomorphic if there exists a bijection $\varphi$ between V(G) and $V(G')$ such that $\varphi$ and its inverse $\varphi ^{-1}$ are both homomorphisms. To enforce the morphisms above to satisfy certain injectivity constraints, the edges of the graphs, in addition to their labels, will have some color as well. In such cases homomorphisms (and hence, subgraph isomorphisms and isomorphisms) are required to preserve the edge colors as well. The definitions of homomorphism, subgraph isomorphism, and isomorphism between directed graphs are analogous with the additional constraint that $\varphi$ must preserve not only the edges, but also their directions. As the generalization of our method from unlabeled graphs to labeled graphs is straightforward, for simplicity we present our algorithms for the unlabeled case.

We will pay a special attention to graphs of bounded tree-width [11]. For the definition and basic properties of bounded tree-width graphs, the reader is referred e.g. to [5]. Given a pattern graph H and a target graph G, it is NP-complete to decide whether there exists a homomorphism from H to G. If, however, the tree-width of H is bounded by some constant, then this problem can be decided in polynomial time for any graph G (see, e.g, [3]). For an integer $k>0$, a k-tree [12] is defined recursively as follows: (i) A clique (i.e., fully connected graph) of $k+1$ vertices is a k-tree. (ii) Given a k-tree G with n vertices, a k-tree with $n+1$ vertices is obtained from G by adding a new vertex v to G and connecting v to all vertices of a k-clique (i.e., a clique of size k) of G. It is well-known that a k-tree has always tree-width k and that it is edge maximal w.r.t. this property, i.e., adding any further edge to a k-tree results in a graph of tree-width $k+1$ (cf. [12]). Furthermore, all k-trees have $k|V(G)| - \left( {\begin{array}{c}k+1\\ 2\end{array}}\right)$ edges. Finally, a partial k-tree is a subgraph of a k-tree and hence has tree-width at most k.

Let $\preceq$ be a preorder (i.e., reflexive and transitive relation) on a set S. For $a,b \in S$ we say that $a \prec b$ iff $a \preceq b$ and $a \nsucceq b$, and define the equivalence relation $\equiv$ on S by $a \equiv b$ iff $a \preceq b$ and $b \preceq a$. A function $\rho : S \rightarrow 2^S$ is called a refinement operator for $(S, \preceq )$ if for every $a \in S$ we have $\rho (a) \subseteq \{ b \in S | a \preceq b \}$. Furthermore, $\rho$ is (i) locally finite if $\rho (a)$ is finite for every $a \in S$, (ii) complete if for every $a,b \in S$ with $a \prec b$ there exist $a \equiv c_0,c_1,\ldots , c_n \equiv b$ with $c_{i} \in \rho (c_{i-1})$ for all $i=1,\ldots ,n$, (iii) proper if for all $a \in S$, $\rho (a) \subseteq \{ b \in S | a \prec b \}$, and (iv) ideal if $\rho$ is locally finite, complete and proper. For basic properties of refinement operators, the reader is referred e.g. to [9].

3 Partially Injective Homomorphisms

In this section we define partially injective homomorphisms, the central notion for this work, and discuss some of their properties. On the one hand, while the homomorphism and subgraph isomorphism problems are both NP-complete in general, their complexity behaves differently on special subproblems. In particular, homomorphism can be decided in polynomial time for a broad range of pattern classes for which subgraph isomorphism remains NP-complete. As an example, whereas the homomorphism problem from graphs of bounded tree-width can be decided in polynomial time [3], subgraph isomorphism remains NP-complete not only from trees (which have tree-width 1), but even from paths. On the other hand, however, as we empirically demonstrate in Sect. 5, frequent patterns generated w.r.t. subgraph isomorphism yield a much higher predictive performance when used for classification purposes than those w.r.t. homomorphism. As subgraph isomorphisms are injective homomorphisms, these empirical results clearly highlight the importance of the injectivity of the pattern matching operator in practice. Motivated by our experiments, we propose a trade-off between complexity and predictive performance by bridging the gap between homomorphisms and subgraph isomorphisms. It follows from the remarks above that a natural transition from homomorphisms to subgraph isomorphisms can be obtained by partial injectivity, i.e., by requiring the injectivity constraint not for all vertex pairs in the pattern, but only for a subset of them. Formally, a pattern graph H can be embedded into a target graph G by a partially injective homomorphism satisfying a set $\mathcal {C} \subseteq [V(H)]^2$ of injectivity constraints, denoted by $H\xrightarrow [\mathcal {C}]{}G$, if there exists a homomorphism $\varphi$ from H to G such that $\varphi (u) \ne \varphi (v)$ for all $uv \in \mathcal {C}$. In case of ordinary homomorphisms, i.e., when $\mathcal {C}= \emptyset$, the above notation reduces to $H \rightarrow G$. We refer to the corresponding decision problem, denoted $\textsc {PIHom}(H,G,\mathcal {C})$, as $\textsc {PIHom}$ problem and call the pair $(H,\mathcal {C})$ a $\textsc {PIHom}$ pattern.

Our key idea is to consider such $\textsc {PIHom}$ problems that can polynomially be reduced to efficiently decidable ordinary homomorphism problems. For the efficiency, we consider graphs of bounded tree-width, utilizing positive complexity results on deciding homomorphisms from this graph class [3]. Regarding the reduction, for H, G, and $\mathcal {C}$ above we transform H and G into two edge colored graphs by the following steps:

• 1. Color all (original) edges of H and G in blue,

• 2. for all $uv \in E(H) \cup \mathcal {C}$, connect u and v by a red edge, and

• 3. for all $u,v \in V(G)$ with $u\ne v$, connect u and v by a red edge.

Let the graphs obtained be denoted by $H\langle \mathcal {C}\rangle$ and $G\langle \top \rangle$. Since there is a one-to-one correspondence between the pair $(H,\mathcal {C})$ and the graph $H\langle \mathcal {C}\rangle$, we sometimes don’t distinguish between the two notions. As homomorphisms between colored graphs preserve also the edge colors, the proof of the claim below is immediate from the definitions, by noting that all graphs considered in this work are loop free:

Proposition 1

For $H,G,\mathcal {C}$ and $H\langle \mathcal {C}\rangle ,G\langle \top \rangle$ above we have $H\xrightarrow [\mathcal {C}]{}G$ if and only if $H\langle \mathcal {C}\rangle \rightarrow G\langle \top \rangle$.

Fig. 1.

Examples for different partially injective homomorphisms from H into G. Solid lines represent blue edges whereas dashed ones represent red edges.

Due to loop-freeness it suffices to consider the injectivity constraints only for unconnected vertex pairs in the original pattern graph H (i.e., we can assume w.l.o.g. that $\mathcal {C} \cap E(H) = \emptyset$). Note also that for H and G above, each subset $\mathcal {C}\subseteq [V]^2 \setminus E(H)$ defines a distinct problem $\textsc {PIHom}(H,G,\mathcal {C})$ and that the set of all $\textsc {PIHom}$ patterns over H form a (complete) lattice $(\mathcal {L}_H, \preceq )$ with

$$\mathcal {L}_H = \{ (H,\mathcal {C}): \mathcal {C}\subseteq [V(H)]^2 \setminus E(H)\}$$

and with partial order $\preceq$ defined as follows: For all $\mathcal {C}_1,\mathcal {C}_2 \subseteq [V(H)]^2 \setminus E(H)$, $(H,\mathcal {C}_1) \preceq (H,\mathcal {C}_2)$ iff $\mathcal {C}_1 \subseteq \mathcal {C}_2$. The least element $(H,\emptyset )$ (resp. greatest element $(H,[V]^2 \setminus E(H))$) of $\mathcal {L}_H$ corresponds to ordinary homomorphism (resp. subgraph isomorphism) from H. For any target graph G, $(\mathcal {L}_H, \preceq )$ is closed downwards in the sense that $H\xrightarrow [\mathcal {C}_1]{}G$ and $\mathcal {C}_2 \subseteq \mathcal {C}_1$ implies $H\xrightarrow [\mathcal {C}_2]{}G$.

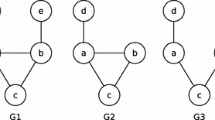
Figure 1 visualizes three partially injective homomorphisms from H into G. The graphs H and G are identical in all three examples, while the sets of injectivity constraints differ. We explicitly visualize the constraints in the depiction of patterns. For instance, the partially injective homomorphism depicted in Fig. 1(b) requires the homomorphism $\varphi$ from H to G to satisfy the injectivity constraint $\varphi (v_2) \ne \varphi (v_3)$.

We will consider lattices of $\textsc {PIHom}$ tree patterns, i.e., when the first component in the $\textsc {PIHom}$ pattern $(H,\mathcal {C})$ is a tree. In particular, when H is a tree with n vertices, the cardinality of the corresponding $\textsc {PIHom}$ pattern lattice $\mathcal {L}_H$ is $2^{O\left( {n^2}\right) }$, i.e., exponential in the size of H. Figure 2 illustrates such a lattice $(\mathcal {L}_H, \preceq )$ for a path H of length 3. Each depicted graph corresponds to a $\textsc {PIHom}$ tree pattern with a specific set of injectivity constraints.

Fig. 2.

Visualization of maximal borders in the lattice of $\textsc {PIHom}$ patterns for a path.

4 Pattern Mining

In this section we define the problem of mining frequent maximally constrained $\textsc {PIHom}$ tree patterns. We first claim that there exists no locally finite and complete refinement operator for a natural representative set of this kind of patterns if we want to avoid redundancy. We therefore relax the problem definition and propose an efficient pattern mining algorithm tolerating redundancies in the output. The restriction of patterns to trees is motivated by complexity issues and by the remarkable predictive performance which is achieved by using frequent subtrees w.r.t. subgraph isomorphism [13]. In general, given a tree H and target graph G, $\textsc {PIHom}(H,G,\mathcal {C})$ can be decided in polynomial time if $\mathcal {C}= \emptyset$ (i.e., for ordinary homomorphism), but is NP-complete whenever $\mathcal {C}= [V(H)]^2 \setminus E(H)$ (i.e., for subgraph isomorphism). We bridge this complexity gap by considering a distinguished subset of $\mathcal {L}_H$ for which the corresponding $\textsc {PIHom}$ problems are decidable in polynomial time for any target graph G. More precisely, for a tree H and some constant $k >0$ we consider the pattern set $\mathcal {L}^k_H= \{(H,\mathcal {C}) \in \mathcal {L}_H: H\langle \mathcal {C}\rangle \text { has tree-width at most }k\}$. Proposition 1 together with the positive complexity result on deciding homomorphisms from graphs of bounded tree-width [3] implies that for all $(H,\mathcal {C}) \in \mathcal {L}^k_H$ and for all target graphs G, $\textsc {PIHom}(H,G,\mathcal {C})$ can be decided in polynomial time.

Our experiments (cf. Sect. 5) clearly demonstrate that, besides the structural gap between homomorphisms and subgraph isomorphisms discussed earlier, there is a large gap between their predictive performances as well. Furthermore, this gap vanishes as the number of injectivity constraints increases. Motivated by this empirical observation and the negative result formulated in Sect. 4.1 below, we will pay a special attention to the maximal elements of $\mathcal {L}^k_H$, i.e., to such $\textsc {PIHom}$ patterns $(H,\mathcal {C}) \in \mathcal {L}^k_H$ for which $H\langle \mathcal {C}\rangle$ is a complete graph whenever $|V(H)| \le k+1$; o/w it is a k-tree. In other words, we will consider the positive border $Bd^+_k$ of $(\mathcal {L}^k_H, \preceq )$ w.r.t. the following interestingness predicate: $(H,\mathcal {C}) \in \mathcal {L}_H$ is interesting if $H\langle \mathcal {C}\rangle$ has tree-width at most k.

As an example, all patterns $(H, \mathcal {C})$ with $|\mathcal {C}|=2$ in Fig. 2 are maximally constrained w.r.t. tree-width 2, as they have tree-width 2 and adding any further constraint would increase their tree-width. (A 4-clique has tree-width 3.) The positive borders for $k=1$ and $k=2$ are denoted by $Bd^+_1$ and $Bd^+_2$, respectively. Clearly, $Bd^+_1 = \{(H,\emptyset )\}$ since adding any further injectivity constraint would result in a pattern of tree-width 2. In the example in Fig. 2 there are e.g. seven constraint sets for the path H connecting $v_1$ and $v_4$. For all of these constraint sets $\mathcal {C}$, $H\langle \mathcal {C}\rangle$ has tree-width at most 2. Yet, we are most interested in the three patterns with $|\mathcal {C}|=2$ (i.e., $Bd^+_2$), as they have the highest degree of partial injectivity.

4.1 $\textsc {PIHom}$ Core Patterns: A Negative Result

Using the concepts introduced above, in this section we consider the pattern language $\mathcal {L}^k$ defined by the union of the $\mathcal {L}^k_H$s over all tree patterns H. Given a database $\mathcal {D}$ of graphs, our goal is to generate a subset S of $\mathcal {L}^k$ on the basis of $\mathcal {D}$ that will span the binary feature space in which the elements of $\mathcal {D}$, as well as further unseen graphs will be embedded. For this application purpose, it is desirable to avoid “redundancies” among the patterns in S. There are various ways of defining redundancy. Perhaps the most natural one is the following definition: S contains no two model equivalent patterns, where the patterns $(H_1,\mathcal {C}_1),(H_2,\mathcal {C}_2) \in \mathcal {L}^k$ are model equivalent, denoted $(H_1,\mathcal {C}_1)\equiv _\text {m}(H_2,\mathcal {C}_2)$, if the equivalence $H_1\xrightarrow [\mathcal {C}_1]{}G \iff H_2\xrightarrow [\mathcal {C}_2]{}G$ holds for all graphs G.

For complexity reasons, we regard a relaxed notion of redundancy and show that even this weaker form raises severe algorithmic issues. More precisely, consider the order $\preceq _\text {h}$ on $\mathcal {L}^k$ defined as follows: For all $(H_1,C_1),(H_2,C_2) \in \mathcal {L}^k$, $(H_1,C_1) \preceq _\text {h}(H_2,C_2)$ iff $H_1\langle \mathcal {C}_1 \rangle \rightarrow H_2\langle C_2 \rangle$. One can easily see that $\preceq _\text {h}$ is a preorder on $\mathcal {L}^k$. Using this definition, a set $S \subseteq \mathcal {L}^k$ is regarded as non-redundant if it contains no two homomorphism equivalent patterns, where $(H_1,\mathcal {C}_1),(H_2,\mathcal {C}_2) \in \mathcal {L}^k$ are homomorphism equivalent, denoted $(H_1,\mathcal {C}_1)\equiv _\text {h}(H_2,\mathcal {C}_2)$, iff $(H_1,C_1) \preceq _\text {h}(H_2,C_2)$ and $(H_2,C_2) \preceq _\text {h}(H_1,C_1)$. Clearly, $\equiv _\text {m}$ and $\equiv _\text {h}$ are both equivalence relations and $\equiv _\text {h}$ is finer than $\equiv _\text {m}$, i.e., the partition of $\mathcal {L}^k$ induced by $\equiv _\text {h}$ is a refinement of that induced by $\equiv _\text {m}$. Thus, model equivalent patterns are not necessarily homomorphism equivalent, implying that $\equiv _\text {h}$ may allow a certain amount of redundancies w.r.t. $\equiv _\text {m}$.

Let $\mathcal {L}^k/ {\equiv _\text {h}}$ denote the set of equivalence classes induced by $\equiv _\text {h}$. For all $c \in \mathcal {L}^k/ {\equiv _\text {h}}$, one can consider the core of c, a canonical representative element of c, defined as follows: Select an arbitrary pattern $(H,\mathcal {C}) \in c$ and take the smallest subgraph $H'\langle \mathcal {C}' \rangle$ of $H\langle \mathcal {C} \rangle$ such that $(H,\mathcal {C}) \equiv _\text {h}(H',\mathcal {C}')$. It holds that $H'\langle \mathcal {C}' \rangle$ (and hence, $(H',\mathcal {C}')$) can be computed by a greedy algorithm removing the redundant edges one by one. The properties of tree-width together with the results of [1, 3] imply that $(H',\mathcal {C}')$ is a core of c, it always exists and is unique modulo isomorphism independently of the choice of $(H,\mathcal {C})$, and can be calculated in time polynomial in the size of $(H,\mathcal {C})$. Let $\mathcal {L}^k_{\text {c}}$ be the set of such cores. The reason of using cores is that in such cases when the pattern matching operator is defined by (relational) homomorphism (e.g. in ILP [9]), the equivalence classes in $\mathcal {L}^k/ {\equiv _\text {h}}$ may contain infinitely many patterns, due to the fact that $\preceq _\text {h}$ is not anti-symmetric.

While subgraph isomorphism as the pattern matching operator allows for a very natural refinement operator on the pattern language, this is typically not the case for homomorphism, caused also by the difference in the anti-symmetry. Indeed, in case of subgraph isomorphism, the pattern language along with the partial order defined by subgraph isomorphism can directly be translated into an ideal refinement operator (assuming that all patterns are connected); just extend the pattern at hand in every possible way either by a single edge or by a single vertex connected to one of the old vertices. In contrast, the preorder on $\mathcal {L}^k$ defined by homomorphism does not impose such an algebraic structure that could be turned into a (natural) algorithmic definition of a refinement operator on $\mathcal {L}^k_\text {c}$. In fact, $\mathcal {L}^k_\text {c}$ may contain cores having infinitely many “direct” refinements, implying the following negative result:

Theorem 1

For all $k\ge 1$, there exists no finite and complete refinement operator for the preordered set $(\mathcal {L}^k_\text {c},\preceq _\text {h})$.

The negative result formulated in Theorem 1 does not imply that $\textsc {PIHom}$ core patterns cannot be enumerated efficiently; this question is an open problem.¹ However, it indicates that traditional pattern generation paradigms based on refinement operators are not applicable to $(\mathcal {L}^k_\text {c}, \preceq _\text {h})$. In the next section we therefore relax our problem setting and tolerate further redundancies in the output pattern set.

4.2 The Problem Definition

Theorem 1 implies that we have to consider a different pattern language in place of $\mathcal {L}^k_\text {c}$ if we want to generate the output patterns by using some algorithmically appropriate refinement operator. To achieve this goal, we consider $\textsc {PIHom}$ tree patterns that are maximally constrained w.r.t. tree-width k, i.e., the set $\mathcal {L}^k_{\max }\subseteq \mathcal {L}^k$ defined as follows: For all $(H,\mathcal {C}) \in \mathcal {L}^k$, $(H,\mathcal {C}) \in \mathcal {L}^k_{\max }$ iff $|V(H)| \le k+1$ and $H\langle \mathcal {C}\rangle$ is a complete graph or $|V(H)| > k+1$ and $H\langle \mathcal {C}\rangle$ is a k-tree. The partially injective homomorphisms obtained in this way are as close as possible to subgraph isomorphism subject to bounded tree-width, resulting in a pattern set of higher predictive performance as shown empirically in Sect. 5. Using this definition, we consider the following pattern generation problem:

• Frequent Maximally Constrained Tree Mining (FMCTM) Problem: Given a finite set $\mathcal {D}$ of graphs and integers $t,h,k > 0$, list all $(H,\mathcal {C}) \in \mathcal {L}^k_{\max }$ such that $|V(H)| \le h$ and $\text {freq}((H,\mathcal {C}),\mathcal {D}) \ge t$, where $\text {freq}((H,\mathcal {C}),\mathcal {D})$ denotes the (absolute) frequency of the $\textsc {PIHom}$ tree pattern $(H,\mathcal {C})$ in $\mathcal {D}$, i.e., $\text {freq}((H,\mathcal {C}),\mathcal {D})= |\{ G \in \mathcal {D}: H\xrightarrow [\mathcal {C}]{}G\}|$.

$\textsc {PIHom}$ tree patterns satisfying the frequency constraint in the definition above will be referred to as frequent $\textsc {PIHom}$ tree patterns, or simply frequent patterns. As mentioned earlier, one of the most important distinguishing features of the problem setting above is that the pattern matching operator is not static (i.e., fixed in advance), but dynamic, in contrast to all traditional frequent graph mining algorithms. Clearly, whether a tree pattern is frequent or not directly depends on the underlying set of constraints applied in the embedding operator. It is therefore necessary to output a frequent tree along with the injectivity constraints defining the (dynamic) pattern matching operator, i.e., the output is always a pair $(H,\mathcal {C})$, instead of H only. Notice that in this work we are not explicitly interested in the semantical properties of the patterns but rather in the binary feature space spanned by them.

The parameter h in the problem definition provides an upper bound on the size of the output patterns. It ensures that the algorithm solving the FMCTM problem will always terminate. It is not difficult to see that without h, the output of the FMCTM problem may contain infinitely many frequent patterns. We also note that the output $\mathcal {O}$ of the FMCTM problem may contain frequent patterns that are homomorphism equivalent. Furthermore, the elements of $\mathcal {O}$ are not necessarily cores. In case the output is required to be a non-redundant subset of $\mathcal {L}^k_\text {c}$, after the computation of $\mathcal {O}$, one can first remove all patterns from it that are redundant w.r.t. homomorphism equivalence and then calculate the core for each pattern remaining in $\mathcal {O}$. Since all patterns in $\mathcal {O}$ have bounded tree-width, both steps can be performed in time polynomial in the size of $\mathcal {O}$.

4.3 The Mining Algorithm

In this section, we present our algorithm solving the FMCTM problem and prove that it is correct and enumerates the output patterns in incremental polynomial time. For the reader’s convenience we ignore a number of (standard) optimization, implementation, and further simplification issues from this short paper and provide only a simplified version of the algorithm implemented.

We guarantee efficiency (i.e., incremental polynomial time) by considering the partial order $\preceq _\text {si}$ on $\mathcal {L}^k_{\max }$, instead of the preorder $\preceq _\text {h}$, where $\preceq _\text {si}$ is defined as follows: For all $(H,\mathcal {C}),(H',\mathcal {C}') \in \mathcal {L}^k_{\max }$, $(H,\mathcal {C})\preceq _\text {si}(H',\mathcal {C}')$ iff there exists a subgraph isomorphism from $H\langle \mathcal {C}\rangle$ into $H'\langle \mathcal {C}' \rangle$. Clearly, $\text {freq}((H,\mathcal {C}),\mathcal {D}) \ge \text {freq}((H',{\mathcal {C}'}),\mathcal {D})$ whenever $H\langle \mathcal {C} \rangle \preceq _\text {si}H'\langle \mathcal {C}' \rangle$, i.e., frequency is anti-monotonic on the poset $(\mathcal {L}^k_{\max },\preceq _\text {si})$. Thus, maximal $\textsc {PIHom}$ tree patterns are closed downwards w.r.t. frequency. While the poset $(\mathcal {L}^k_{\max },\preceq _\text {si})$ allows for efficient pattern enumeration, the output may contain patterns that are homomorphism equivalent. That is, the price we have to pay for the positive complexity result is that the output may contain some redundant patterns.

Algorithm 1 is based on the recursive function Enumerate generating the output patterns in a DFS manner. Its input consists of the same parameters $\mathcal {D}$, t, h, and constant k as the FMCTM problem. The output patterns already generated are stored in the global variable $\mathcal {O}$. The algorithm calls $\text {Enumerate}$ with the empty pattern $(\bot ,\emptyset )$, where $\bot$ denotes the empty graph (line 2 of Main). As a first step (line 1 of Enumerate), function Refinements generates the set of refinements for the input pattern $(H,\mathcal {C})$; the process governing how new candidate patterns are generated is determined by the refinement operator sketched below. If a newly generated candidate pattern $(H',\mathcal {C}')$ (i) fulfills the size constraint (i.e, $|V(H')| \le h$), (ii) has not been generated before (i.e., $(H',\mathcal {C}') \notin \mathcal {O}$), and (iii) is t-frequent (i.e., $\text {freq}((H',\mathcal {C}'),\mathcal {D}) \ge t$), we print it, store it in $\mathcal {O}$, and call Enumerate recursively for this new frequent pattern (lines 3–5).

Refinement Operator. Function Refinements in Algorithm 1 returns the set R of refinements for a pattern $(H,\mathcal {C}) \in \mathcal {L}^k_{\max }$ and $k >0$. All patterns $(H',\mathcal {C}') \in R$ are required to satisfy the following conditions: (i) $H'$ is a supertree of H obtained by extending H with a new vertex and edge, (ii) $\mathcal {C}\subseteq \mathcal {C}'$, and (iii) $(H',\mathcal {C}') \in \mathcal {L}^k_{\max }$, i.e, it is maximal w.r.t. tree-width k. That is, trees of size n are extended into trees of size $n+1$ by condition (i). Furthermore, condition (iii) implies that $H'\langle \mathcal {C}' \rangle$ is a k-tree if $|V(H')| > k+1$; o/w it is a complete graph.

The algorithmic characterization of k-trees (cf. Sect. 2) gives rise to the following natural refinement operator on $\mathcal {L}^k_{\max }$: A pattern $(H',\mathcal {C}')$ of size $n+1$ is among the refinements of a pattern $(H,\mathcal {C})\in \mathcal {L}^k_{\max }$ of size n iff $(H',\mathcal {C}')$ can be obtained from $(H,\mathcal {C})$ in the following way: If $n=0$ (i.e., $(H,\mathcal {C})=(\bot ,\emptyset )$), we define the refinements of $(H,\mathcal {C})$ by the set of graphs consisting of a single vertex (and no edges, as we consider loop-free graphs).² Otherwise, i.e., for $n > 0$, we proceed as follows: (i) Introduce a new vertex u. (ii) If $n \le k$, then connect u to a vertex $v \in V(H)$ and add an injectivity constraint $uv'$ to $\mathcal {C}$ for every $v' \in V(H) \setminus \{v\}$; o/w select a k-clique C in $H\langle \mathcal {C} \rangle$, connect u to a vertex v of C in H, and add an injectivity constraint $uv'$ to $\mathcal {C}$ for every $v' \in V(C) \setminus \{v\}$.

We are ready to state our main result:

Theorem 2

For any $\mathcal {D}$, t, k, and h, Algorithm 1 is correct and generates the output patterns in incremental polynomial time.

5 Experimental Evaluation

This section is concerned with the empirical evaluation of our approach. In particular, we evaluate the predictive performance of frequent maximally constrained $\textsc {PIHom}$ tree patterns and the runtime of the algorithm presented in Sect. 4. For our experiments we used a modified variant of Algorithm 1 making it practically feasible. We omit these technical details from this short version.

In the experiments below we first analyze how the degree of injectivity in $\textsc {PIHom}$ tree patterns impacts the resulting predictive performance. To answer this question, we fix a set of tree patterns and embed the data into feature spaces spanned by the tree patterns w.r.t. partially injective homomorphisms with increasing degree of injectivity, ranging from ordinary homomorphism to subgraph isomorphism. Our results clearly indicate a strong correlation between degree of injectivity and predictive performance. We then compare the predictive performance of the patterns generated by our practical algorithm with that of ordinary frequent subtrees on different benchmark datasets. We found that the predictive performance achieved by $\textsc {PIHom}$ tree patterns for already moderate amounts of injectivity constraints compares favorably to that of ordinary frequent subtrees, which, in turn, are very close to frequent subgraphs in predictive power. Finally, we provide runtime measures comparing our algorithm to state-of-the-art graph miners like GASTON [10] and FSG [4]. We show that while these algorithms are practical only for very restricted graph types, our approach performs well on arbitrary graph datasets. In particular, while our implementation was generally slower on the real-world benchmark chemical graph datasets considered, it clearly outperforms GASTON [10] and FSG [4] on artificial datasets containing only slightly more complex graph structures beyond molecular graphs.

Datasets. To evaluate the predictive performance, we use four benchmark molecular graph datasets. This choice is mainly of practical nature. In particular, the molecules considered are of a fairly simple structure [8], allowing for the application of state-of-the-art frequent subgraph mining systems that are generally very efficient on molecular graph data. This enables us to compare the predictive performance of our method to “gold-standard” results achieved by frequent subgraphs (w.r.t subgraph isomorphism).

The experiments are conducted on the well-established real-world datasets NCI1, NCI109, MUTAG, and PTC annotated for different binary target properties. NCI1 and NCI109 contain 4,110 (resp. 4,127) compounds. The graphs in these two datasets have 30 vertices and 32 edges on average. The MUTAG dataset contains merely 188 compounds; the graphs in this dataset have 18 vertices and 20 edges on average. Finally, the PTC dataset contains a total of 344 graphs, with an average number of 26 vertices and edges.

As most frequent subgraph mining systems like GASTON [10] are specifically designed to cope with graphs of simple structure (such as molecular graphs), runtime comparisons on only chemical graph datasets are not expressive enough. We therefore consider also artificial graph datasets generated according to the Erdős-Rényi random graph model. Each such dataset consists of 50 graphs with an average size of 25, corresponding to the chemical datasets above. The structural complexity of these graphs G corresponds to the edge/vertex ratio $q=|E(G)|/|V(G)|$. In our experiments, only connected graphs are considered.

Experimental Setup. Using 10-fold cross-validation, the predictive performance was measured in terms of AUC obtained by support vector machines (SVM) with the RBF kernel. In all experiments we used LIBSVM [2]. We applied SVM to the images of the graphs in the binary feature space spanned by the frequent patterns generated. The parameters of SVM (i.e. C and $\gamma$) were fixed throughout all classification tasks for a given database to avoid overfitting by chance. For all frequent pattern generation methods, we chose a frequency threshold value of $5\%$. Prior experiments have shown that patterns of fairly low sizes achieve the overall best predictive performances. We therefore limit the size of patterns to at most 9 vertices.

Fig. 3.

Predictive performances in AUC for different degrees of injectivity governed by tree-width k. $k=\top$ corresponds to ordinary subgraph isomorphism.

5.1 Degree of Injectivity vs. Predictive Performance

We first report our results investigating the influence of the degree of injectivity in $\textsc {PIHom}$ tree patterns on the predictive performance. To exclude possible side-effects caused by different pattern sets, for all datasets in our experiments we first fix a set S of tree patterns by selecting some random subset of the frequent trees generated w.r.t. subgraph isomorphism. Then, for all $H \in S$ we consider a $\textsc {PIHom}$ tree pattern $H_k = (H,\mathcal {C}_k)$ that is maximally constrained w.r.t. tree-width k if $k =1,\ldots ,4$; o/w it is fully constrained, i.e., $\mathcal {C}_\top = [V(H)]^2 \setminus E(H)$. Since H is a tree, $\mathcal {C}_1 = \emptyset$ and hence $H_1$ is the least element in the lattice $(\mathcal {L}_H,\preceq )$, corresponding to ordinary homomorphism from H. Analogously, $H_\top$ contains all possible injectivity constraints and is therefore the greatest element of $(\mathcal {L}_H,\preceq )$, corresponding to ordinary subgraph isomorphism from H. In this way we can simulate monotonically increasing degrees of injectivity in the pattern matching operator for a tree pattern H, leading from ordinary homomorphisms to subgraph isomorphisms. The degree of injectivity in the pattern matching operator is directly governed by k. For all $k \in \{1,\ldots ,4,\top \}$ we take the feature set $S_k = \{ H_k : H \in S\}$ and embed all target graphs into the binary feature space spanned by $S_k$ in the usual manner.

Figure 3 shows the predictive performances achieved for different degrees of injectivity defined by k. All four datasets indicate a significant difference between employing homomorphism ($k=1$) and subgraph isomorphism ($k=\top$) as the pattern matching operators. While the results for MUTAG and PTC are fairly volatile due to their small size, with $k=3$ and subgraph isomorphism yielding the best results, the datasets NCI1 and NCI109 clearly show a direct correlation between the degree of injectivity and predictive performance: Increasing values of k in almost every case yield an improvement in predictive performance. Notice that the gap between $k=1$ (i.e., ordinary homomorphism) and $k=2$ is already substantial for the datasets NCI1 and NCI109. For MUTAG and PTC it seems that $k=3$ is necessary to significantly improve the predictive performance over homomorphism. In summary, a fairly low degree of injectivity already suffices to considerably outperform the predictive power of ordinary homomorphism.

Table 1. Prediction measures stated as AUC values in % for different tree-width choices k in contrast to freq. subgraphs and subtrees (s.g.i.: subgraph isomorphism, p.i.h.: partially injective homomorphism). Values are calculated by a SVM on feature vectors w.r.t. pattern graphs of size at most |V|.

5.2 Predictive Performance

We also evaluate the predictive performance of the frequent maximally constrained $\textsc {PIHom}$ tree patterns generated by our algorithm. We compare their predictive power to that achieved by the set of (ordinary) frequent subtrees, as well as frequent subgraphs w.r.t. subgraph isomorphism. The binary feature vectors for the target graphs are calculated in the same way as described in the previous section for the patterns generated by our algorithm, for ordinary frequent subtrees, and for ordinary frequent subgraphs.

Table 1 shows the predictive performance of our approach for different pattern sizes (cf. the last five columns). The full sets of frequent subgraphs perform slightly better than its subset formed by frequent subtrees. Interestingly, already for tree-width $k=3$, the absolute difference (in AUC) to frequent subgraphs (cf. row “s.g.i. graphs”) and to ordinary frequent subtrees (cf. row “s.g.i. trees”) is marginal for all cases, but one (MUTAG with $|V|=5$). In all cases, the differences are statistically insignificant (for $p=0.05)$. Hence, our approach offers an attractive trade-off between runtime (depending on k) and predictive power.

Table 2. Runtimes (in sec.) of our algorithm in comparison to GASTON and FSG on molecular and artificial datasets. $\varSigma$ denotes the set of vertex labels. The cases in which GASTON ran out of the necessary memory are marked by “mem err”. The maximum size of patterns to be found was set to 10 and the minimum support was set to $5\%$ in all cases. Note that FSG does not restrict its search to trees but considers general graphs, in contrast to all other algorithms.

5.3 Runtimes

We measured the runtimes of our algorithm and compared them to those achieved with the state-of-the-art graph miners GASTON [10] (using the graph counting methods embedding lists (EL) and recomputed embeddings (RE)) and FSG [4] on real-world and artificial datasets. While molecules, having roughly as many edges as vertices (i.e., having $q \approx 1.0$), q is up to 3.0 in the artificial datasets.

Table 2 shows the running times for each algorithm and dataset. As expected, GASTON and FSG perform very well on molecular graphs, compared to our algorithm. However, for slightly more complex structures (i.e. $q \ge 2.0$) the two traditional graph miners become quickly infeasible for the correlation between the number of embeddings and runtime. Our approach (referred to as PIH Miner in Table 2) clearly outperforms FSG and GASTON on both artificial datasets for $q \ge 2.0$.

6 Concluding Remarks

To bridge the gap between homomorphisms (ILP) and subgraph isomorphisms (graph mining), we proposed partially injective homomorphisms, a new kind of dynamic pattern matching operator. We considered the efficiently enumerable fragments of frequent maximally constrained $\textsc {PIHom}$ tree patterns w.r.t. bounded tree-width and showed on benchmark molecular graph datasets that their predictive performance is close to that of ordinary frequent subtrees (and hence, to that of subgraphs as well). Since our algorithm does not assume any structural properties on the input graphs, it is effectively applicable also to such transaction graphs where most state-of-the-art pattern mining algorithms become infeasible.

Our approach raises several questions. Perhaps the most interesting one is the extension to more general relational vocabularies, bridging another gap between graph mining and ILP in the richness of the relational vocabularies. To formulate this generalization, we note that any $\textsc {PIHom}(H,G,\mathcal {C})$ problem can polynomially be reduced to $\theta$-subsumption between DATALOG goal clauses (or equivalently, Boolean conjunctive queries) as follows: Using a relational vocabulary $\varSigma$ consisting of binary and unary predicate symbols only, represent $(H,\mathcal {C})$ as a DATALOG goal clause $Q_H$ with a body composed of a set of literals for H and another set of literals of a distinguished binary predicate for the injectivity constraints in $\mathcal {C}$. Each vertex of H is represented by a unique variable in $Q_H$. For a target graph G, represent the $\textsc {PIHom}$ pattern $(G, [V(G)]^2)$ in a similar way by a clause $Q_G$ over the same $\varSigma$. It holds that $Q_H$ $\theta$-subsumes $Q_G$ iff $H\xrightarrow [\mathcal {C}]{}G$. From this reduction and our empirical results it is immediate that the predictive performance of DATALOG goal clauses as patterns can also be improved by adding injectivity constraints (i.e., literals of a distinguished binary predicate) to their bodies. Considering our approach developed for graphs from the above logical viewpoint, it would be interesting to generalize it to relational vocabularies containing predicate symbols of arbitrary arities by considering such fragments of Boolean conjunctive queries for which $\theta$-subsumption is in P (cf. [6]).