Keywords

1 Introduction

The Immune System (IS) is the ensemble of cells and molecules that protects living organisms from foreign pathogens. This complex machinery consists in a set of mechanisms whose complexity depends on the evolutionary level of the host. In mammals, besides the innate immunity, the adaptive immunity represents the most effective weapon against viruses and bacteria, thanks to its ability to specifically recognize and act against pathogens (specificity), to discriminate between self and non-self, and to remember previously encountered pathogens in order to act more rapidly (memory). While being extremely effective, adaptive immunity is not faultless. A breakdown of the mechanisms that allow the IS to discriminate between self and non-self antigens may lead to harmful effects, such as the arise of autoimmune diseases. Multiple sclerosis (MS), a disease of the Central Nervous System (CNS), falls within those.

MS is a chronic inflammatory disease that causes the removal of myelin sheath created by oligodendrocytes from axons, leading to a reduced functionality of the CNS. It is well known that a genetic predisposition correlates with MS [8]. Moreover, environmental and dietary factors may play an important role. Epstein-Barr virus (EBV) may trigger the disease onset [17, 18], while it is supposed that vitamin D could help in preventing MS [11]. Symptoms include weakness and fatigue, blurry vision, speech problems, numbness and tingling, dizziness, lack of coordination and uncontrolled bodily functions. The most common form of MS (80−90% of the total insurgence) is Relapsing-Remitting MS (RRMS) [20], where relapses (periods of disease progression) are followed by periods of remission (total or partial recovery from symptoms). RRMS usually occurs in the age of 20−40, with a women-to-men ratio of 2:1. When left untreated, \(65\%\) of RRMS cases turn after 15−25 years to more severe MS forms [7].

Even if the etiology of MS is not fully understood, the common shared hypothesis suggests that self-reactive T lymphocytes may be activated in the periphery by an external trigger (i.e., EBV). Activated T cells can overcome the blood brain barrier and go through the CNS [24]. Once in the brain, self-reactive cells cause inflammatory events that negatively affect both myelin and oligodendrocytes, also involving other IS entities such as B lymphocytes, macrophages, and microglia. It is worth noting that relapses usually represent the clinical correlates of inflammatory bouts. Self-reactive T lymphocytes represent one of the main actors in the development and progression of the disease, as such cells tend to decrease in the peripheral blood while increasing in the spinal fluid when relapses occur. Furthermore, homeostasis of regulatory T cells (Treg) and effectors T cells (Teff) is fundamental in preventing autoimmunity [9, 13]. More precisely, a breakdown of the peripheral tolerance mechanisms, such as the lack of functionality or deficiency of Treg functions, may bring to uncontrolled activation and proliferation of effectors T cells [19].

This hypothesis has been confirmed by Vélez de Mendizábal et al. [23], with the use of an Ordinary Differential Equations (ODEs) model capable of reproducing the behavior of RRMS. However, this model represented a very simplistic scenario, by avoiding to explicitly include the trigger of the disease represented by an external factor such as the EBV, as well as the occurrence of neural damage represented by the loss of myelin and/or the death of oligodendrocytes. Furthermore, the model totally missed to give any description of the spatial evolution of the disease. These issues were fulfilled by an agent based model (ABM) capable of better describing, from a temporal and spatial points of view, the typical shape of RRMS [16]. It must be said that, due to the significant computational efforts needed to run thousands of ABM simulations, a deeper analysis of the model parameters that may influence the disease progression was not carried out.

To cope with these aspects, in this paper we propose a new framework for the analysis of this type of biological systems, in which a graphical formalism is exploited to facilitate the model creation and the simulation of its behavior. In detail, Stochastic Symmetric Net (SSN) [6], a high-level Petri Nets formalism, is used to describe the system in a parametric and compact manner. Then, from the SSN model an ODE system is automatically derived and solved through a numerical integrator that exploits a High Performance Computing solution. In particular, a GPU-based simulation algorithm of ODE systems is suitable in this context [15], since models translated from SSNs into set of equations typically involve thousands of reactions and/or chemical species. It is therefore necessary to accelerate the numerical integration to achieve thorough analyses of the system. Here we exploit an improved version of LASSIE [22], a GPU-powered deterministic simulator capable of realizing both a fine-grained and a coarse-grained parallelization, meaning that the calculations required by a single simulation are distributed over the GPU cores, as well as multiple simulations that run in a parallel fashion on the GPU.

We show that this novel framework that combines SSNs with LASSIE may provide a good compromise between its effectiveness in terms of model description and solution, and the mathematical and computational skills needed to generate, simulate and analyse models.

The paper is structured as follows. In Sect. 2 we briefly recall the basic notions of SSN and the functioning of LASSIE, while in Sect. 3 we describe the SSN model of MS. In Sect. 4 we present our developed framework and the results of the parameter sweep analysis executed on the RRMS model. We conclude in Sect. 5 with some final remarks and future directions of this work.

2 Background

In this section we introduce all the definitions, notations and methods used in the rest of the paper. We first introduce the SSN formalism and then we describe how to translate a SSN model into the corresponding (symbolic) ODE system. Finally, we briefly describe LASSIE, the GPU-powered deterministic simulator exploited to realize the analysis of the RRMS model.

2.1 The SSN Formalism

Stochastic Symmetric Net (SSN) is a high-level graphical formalism that extends Stochastic Petri Net (SPN) formalism with colored tokens [6], so that an information can be associated with tokens flowing in the net. This feature allows for a more compact system representation that can be exploited during both the construction and the solution of the model [1, 3, 6]. SSN is a bipartite directed graph with two types of nodes, called places and transitions.

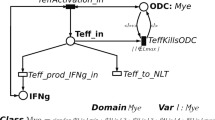
The places, graphically represented as circles, correspond to the variables describing the state of the system. Places can contain colored tokens, whose colors are defined by the color domain cd() associated with any place. The place color domains are thus defined as Cartesian products of color classes \(C_i\), or by the neutral element \(\epsilon \) consisting of a neutral color as in ordinary Petri Nets. A color class \(C_i\) can be partitioned into static sub-classes \(C_{i,1} \; \cup \; \ldots \; \cup \; C_{i,l}\). Then, the colors of a class represent entities of the same nature (e.g., regulatory T cells), but only the colors within a static sub-class are guaranteed to behave similarly (e.g., regulatory T cells in active state). Moreover, a color class is ordered if and only if it is possible to define on it a successor function, denoted by \(++\), which determines a circular order on its elements. For instance, in the SSN model in Fig. 1, three color classes are defined: State denoting the cell state, PosX and PosY encoding the cell position on a grid representing a tissue portion. The color class State is divided into two static sub-classes N and A, which refer to the cell states Naive and Active, respectively. Differently, the ordered color classes PosX and PosY are not divided into static sub-classes. According to this color definition, the color domain of places Treg and Teff is \(State \times PosX \times PosY \). Differently, the color domain of places ODC and EBV is \(PosX \times PosY \).

The transitions, graphically represented as boxes, correspond to the system events. The possible colored instances of a transition are defined by the color domain cd() associated with any transition. The transition color domains are thus expressed through a list of typed variables, whose types are selected among the color classes \(C_i\). The variables associated with a transition appear in the functions labeling its arcs, so that a transition instance binds each variable to a specific color of proper type. Then, a guard can be used to introduce restrictions on the allowed instances of a transition. Such restrictions are defined as Boolean expression over the color domain of the transition, and their terms, called basic predicates, allow one (i) to compare colors assigned to variables of the same or different type (\(x=y,x \ne y\)); (ii) to test whether a color element belongs to a given static sub-class (\(x \in C_{i,j}\)); (iii) to compare the static sub-classes of the colors assigned to two variables (\(x,y \in C_{i,j}\)). For instance, the color domain of transition TeffActivation in Fig. 1 is \(State \times State \times PosX \times PosY \). The guard \([m \in N \; \wedge \; n \in A]\) is associated with this transition to mimics the activation of a Naive Teff cell.

The functions labeling arcs are formally expressed as sums of tuples where each tuple element is chosen from a set of predefined basic functions, whose domains and co-domains are respectively color classes and multisets on color classes. The basic functions in SSN formalism can be grouped as follows: projection functions, denoted by a variable in the transition color domain (e.g., m, x and y appearing in the arc expression \(<m,x,y>\) labeling several arcs in net); successor functions, denoted by \(x++\), where x is a variable in the transition color domain whose type is an ordered class; a constant function returning all elements in a class (or sub-class), indicated as classname.All. Input, output arcs are denoted by \(I,O[p,t]:\) \( cd (t) \rightarrow Bag[ cd (p)]\), where Bag[A] is the set of all possible multisets that may be built on set A.

The state of an SSN, called marking, is defined by the number of colored tokens in each place. For instance, a marking for the model in Fig.1, assuming \(N=\{n\}\), \(A=\{a\}\), PosX\(=\{x_1, \dots ,x_n\}\) and PosY\(=\{y_1, \dots ,y_n\}\), is

$$m=Treg (10\langle n,x_1 ,y_2\rangle )+Teff ( 12\langle a,x_2 ,y_2\rangle ),$$

representing the state in which there are 10 Treg cells in position \(x_1,y_2\) and 12 Teff cells in position \(x_2 ,y_2\).

The evolution of the system is given by the firing of an enabled transition, where the enabling condition and the state change associated with each transition instance are specified by means of arc functions labeling the arcs connecting a place to this transition and vice versa. Given the color identifying an instance of the transition t, the arc function labeling the arc connecting t to a place p provides the (multi)set of colored tokens that will be either added to or removed from p. In the SSNs, the firing of an enabled transition instance \(\langle t,c \rangle \) occurs after a random delay sampled from a negative exponential distribution whose rate is given by:

$$ \omega (t,c)= \left\{ \begin{array}{ll} r_i &{} cond _i(c)\ \forall i=1,\dots ,n,\\ r_{n+1} &{} otherwise ,\\ \end{array} \right. $$

where \(cond_i\) is a Boolean expression comprising standard predicates on the transition color instance. In this manner, the firing rate \(r_i\) of a transition instance can depend only on the static sub-classes of the objects assigned to the transition parameters and on the comparison of variables of the same type. We assume that the conditions \(cond_i\) are mutually exclusive. So doing, the stochastic process mimicking the dynamic of SSN models is a Continuous Time Markov Chain (CTMC), where the states are identified with SSN markings and the state changes correspond to the marking changes in the SSN.

If we assume that all the transitions of the SSN use an infinite server policy, the transition rate from state m to state \(m'\) in the CTMC can be written as:

$$ q_{m,m'}= \sum _{\forall t,c: m {\mathop {\longrightarrow }\limits ^{\langle t,c \rangle }}m'} \omega (t,c)e(m,t,c), $$

where e(m, t, c) is the enabling degree of the transition instance \(\langle t,c \rangle \) in marking m, defined as:

$$ e(m,t,c) = \min _{(p_j,c'):I[p_j,t](c)(c')\ne 0 } \left\lfloor \frac{m(p_j)(c')}{I[p_j,t](c)(c')} \right\rfloor . $$

According to these assumptions, the temporal behavior of an SSN model can be derived by means of analytic or numerical approaches [21]. However, in the case of very complex models, the underlying CTMC can not be derived or/and solved due to the well-known state space explosion problem. To deal with these cases, whenever the stochasticity of the modeled system can be neglected (e.g., due to huge number of cells), the so-called deterministic approach [12] can be exploited, assuming that the behavior of entities contained in a place of the net is described with an ODE and that the whole model is specified with a system of ODEs, one for each place of the net.

2.2 From SSN Models to ODEs

Starting from Kurtz’s results [12], in [3] we described how to efficiently derive an ODE system that provides a good deterministic approximation for the stochastic behavior of the corresponding SSN model. Practically, a SSN model is firstly translated into its equivalent SPN through the unfolding procedure [3], which consists of replicating places and transitions as many times as the cardinalities of the corresponding color domains. Hence, colors disappear in the unfolded model and the complex behavior due to color combinations, color arc functions and color transition guards, is encoded with a net structure in which tokens are indistinguishable entities and new transitions, places and arcs are introduced to account for the different actions performed by instances of the same transition on colored tokens. Note that the name of new places (transitions) in the unfolded net is defined by associating with the original name of the place (transition) in the SSN one possible element of its color domain. For instance, the unfolding of the SSN p place, with \(cd(p)=C \times C\) and \(C=\{c1,c2\}\), will provide four places: \(p_{c1,c1}\), \(p_{c1,c2}\), \(p_{c2,c1}\) and \(p_{c2,c2}\).

When the unfolded SPN model is derived, the average number of tokens in each place of the unfolded net is approximated through the following ODE:

$$\begin{aligned} \frac{dx_i(\nu )}{d\nu }=\sum _{j =1}^{|T|}s(t_j,x(\nu ))(O[p_i,t_j]-I[p_i,t_j]), \end{aligned}$$
(1)

where \(x(\nu )\) is a vector of real numbers representing the average number of tokens in the model places at time \(\nu \), T is the set of the net transitions, and \(s(t_j,x(\nu ))\) is a function defining the speed of transition \(t_j\) in the state \(x(\nu )\) as follows:

$$\begin{aligned} s(t_j,x(\nu ))=\omega (t_j)\min _{l:I(p_l,t_j)\ne 0} \frac{x_l(\nu )}{I[p_l,t_j]}. \end{aligned}$$
(2)

2.3 LASSIE: GPU-Powered Simulation of Large-Scale Models

LASSIE is a GPU-powered deterministic simulator that can be easily used without any specific GPU programming or ODE modeling skills [22]. LASSIE was designed to perform deterministic simulations of large-scale biochemical models, distributing all required calculations on the cores of the GPU. LASSIE requires as input a biological system formalized as a reaction-based model [4, 10] under the assumption of mass-action kinetics [14], as in the case of SSN models translated into ODE systems (see Sect. 2.2). LASSIE was developed using the most widespread GPU computing library, namely, Nvidia Compute Unified Device Architecture (CUDA), which allows programmers to exploit the GPUs for general-purpose computational tasks (GPGPU computing).

In this work, we make use of an improved version of LASSIE that realizes both a fine-grained and a coarse-grained parallelization of the simulations. This means that two different levels of parallelism are implemented: (i) the numerical integration of ODEs required by a single simulation is parallelized on the GPU cores, and (ii) many simulations of the same model characterized by different initial conditions and kinetic parameters are executed in a parallel fashion on the same GPU. The second level of parallelization was introduced to the aim of fully occupying the GPU cores, and to further accelerate the analysis of large-scale models of biological systems.

3 Treg-Teff Cross Regulation in RRMS

Our case study, as already anticipated in Sect. 1, refers to the cross regulation mechanism between Treg and Teff cells in RRMS. T cells are a type of white blood cells that play a central role in the human immune system. Indeed, they implement the adaptive immunity that tailors the immune response of the body to specific pathogens. T cells are commonly divided into various populations, including Cytotoxic CD8 T lymphocytes, also known as effectors T cells (Teff), the main effectors of cellular-mediated immunity that can directly attack infected or cancer cells, and CD4 T helper lymphocytes, essential to boost the immune functions by activating other immune cells. More recently, regulatory T cells (Treg) have been discovered as one of the main actors in modulating the immune system in order to maintain tolerance to self-antigens and to prevent autoimmune diseases. In particular, Treg cells are usually responsible of controlling the Teff functionalities suppressing their potentially deleterious activities. Teff cells can be inhibited by Treg cells through cell-to-cell contact and immunosuppressive cytokines. Furthermore, Treg proliferation can be stimulated as a consequence of the suppression of Teff cells. In our study we consider the activation of self-reactive Teff and Treg cells due to an EBV infection that, through a process called antigenic mimicry, misleads such cells. In this situation, in healthy people, Treg cells are able to control the spread of Teff cells activated by EBV. Instead, in diseased people a breakdown of the regulation mechanism, represented by a malfunction of Treg activities, leads to widespread inflammatory events driven by Teff cells that erroneously attack the Myelin Based Protein (MBP), a major structural component of myelin that is expressed by oligodendrocytes (ODC) in the central nervous system. This attack can irredeemably damage myelin sheath of neurons leading to the occurrence of demyelinating diseases as MS.

Fig. 1.
figure 1

SSN model describing Treg-Teff cross regulation in multiple sclerosis.

Full size image

Figure 1 shows the SSN model describing our case study. The color class State divided into two sub-classes (i.e. Naive and Active) represents the cell status, while the ordered color classes PosX and PosY encode the cell position considering the tissue portion as spherical grid. The marking of places Teff (resp. Treg) provides the number of active and inactive Teff (resp. Treg) cells in each grid position. Similarly, the marking of places EBV and ODC represents the concentration of EBVs and ODCs in each grid position.

The Teff, Treg, and EBV diffusion process is modeled by the transitions MoveTeff, MoveTreg and MoveEBV. The proliferation of inactive Teff and Treg cells is modeled by the firing of the transitions TeffBorn and TregBorn, while their natural death by the firing of the transitions TregDeath and TeffDeath. The activation of a Teff cell due to the contact with EBV is modeled by the transition TeffActivation. Similarly, the transition TregActivation represents the activation of a Treg cell due to the contact with EBV. The transition TeffKillsODC describes the attack of Teff against ODCs causing the axonal damage. Moreover, as a feedback, the Teff cell will be duplicated. The partial recovery (recoverable damage) of ODC functions up to their initial value is instead represented by the transition recovery. Finally, the transition TregKillsTeff is used to model the already described down regulation functions of Treg cells against Teff cells.

4 Results

4.1 Framework Architecture

In this section we describe the architecture of the prototype framework that we developed for the study of Treg-Teff cross regulation in RRMS. This framework is integrated in GreatSPN [2], a well-known suite for the analysis of Discrete Event Dynamic Systems described through Petri Net formalisms. In details, our framework exploits the GreatSPN GUI to draw an SSN model and to derive the corresponding ODE system from an SSN model, while LASSIE [22] is used for solving the generated ODE system. The architecture of this prototype framework is depicted in Fig. 2: GreatSPN is used as graphical interface for constructing the model and as solution manager for activating the solution process. The solution manager executes in the correct order the framework components, and manages the models/data exchanges between them.

Fig. 2.
figure 2

Schematization of the prototype framework combining GreatSPN suite with LASSIE (the components are shown by rectangles, component invocations by solid arrows, models/data exchanges by dashed arrows).

Full size image

Thus, the solution process comprises three steps:

  1. 1.

    Unfolding to derive the unfolded SPN model from an SNN model, as described in Sect. 2;

  2. 2.

    PN2ODE to generate the ODE system from an SPN model, as formalized in Sect. 2. Then, the derived ODE system is exported according to the LASSIE input format;

  3. 3.

    LASSIE to solve the generated ODE system by offloading onto the GPU all the calculations required by the numerical integration of all parallel simulations.

4.2 Computational Results

To test the effectiveness of the pipeline presented in Sect. 4.1, we performed a parameter sweep analysis (PSA) [5] on the RRMS model, in which one kinetic parameter was varied within a given sweep interval (chosen with respect to a fixed reference value for each parameter). For this test we exploited a Nvidia GeForce GTX Titan Z (2880 cores, clock 876 MHz, RAM 6 GB).

The RRMS model depicted in Fig. 1 was converted into an ODE system characterized by 3200 reactions and 700 chemical species. The PSA was performed by generating a set of different initial conditions—corresponding to different parameterizations of the model—and then automatically executing the parallel deterministic simulations with LASSIE. The initial marking, the transition rates and the grid size used in the experiments are reported in Fig. 1. The kinetic constant associated with the firing of the TregKillsTeff transition was varied by taking 640 different values equally distributed in the interval \([10^{-3},1]\) days\(^{-1}\). We recall here that the firing rate of such transition is fundamental to describe the possible malfunction of Treg cells activities, which may lead to a breakdown of the peripheral tolerance and thus to the insurgence of the disease.

Fig. 3.
figure 3

Dynamics of Teff (left) and ODC (right) with different values of the kinetic constant associated with the TregKillsTeff transition. (Color figure online)

Full size image

The results of this analysis are reported in Fig. 3, where we can observe that for values of the kinetic constant higher than \(0.109 \text{ days }^{-1}\), Treg cells are able to control the spread of Teff cells (left panel, yellow and purple lines) and consequently to avoid the appearing of the disease. This is also visible on the ODC plot (right panel, yellow and purple lines) that shows how the amount of ODC, even if initially lowered due to the Teff actions, goes rapidly back to its maximum value, suggesting that any damage has been avoided or recovered at most (recoverable damage). This outcome well describes the scenario of healthy people, in which the peripheral tolerance is able to compensate for a genetic predisposition in developing the disease. For values of the kinetic constant lower than \(0.109 \text{ days }^{-1}\), an oscillatory behavior of Teff starts to appear (left panel, red line), becoming more and more pronounced as the value of the kinetic constant decreases (i.e., left panel, black line). In this scenario, it is possible to observe that the amount of ODC decreases to around zero in correspondence to each peak in the number of Teff (left panel, red and black lines), suggesting an ongoing inflammation that causes neural damage, and thus the possibility of relapses in correspondence of each peak in the Teff amount. Interestingly, a fixed initial quantity of EBV seems to be sufficient to start such oscillatory behavior that can be correlated to multiple relapses. This is somewhat different from the models presented in [16, 23], where each relapse was triggered by a single spread of virus.

For what concerns the computational time required to execute the PSA on the GPU, by considering the time necessary to run a single simulation with a C++ implementation of Dormand and Prince method, exploiting a single core of a CPU Intel Core i7-6700HQ, 2.6 GHz, we estimated a speed-up around \(97\times \) on the Nvidia GeForce GTX Titan Z, thanks to the parallelization provided by LASSIE.

5 Conclusions

In this paper we presented a novel framework for the analysis of complex biological systems. This framework combines the descriptive power of Stochastic Symmetric Nets, which allows one to provide a graphical representation of complex biological systems in a compact and parametric way, with a tool that automatically derives a system of ODEs corresponding to the net. The resulting ODEs system is typically composed of hundreds or thousands of reactions and/or chemical species; it is therefore essential to accelerate the simulations by means of a High Performance Computing solution. In our framework we exploit LASSIE, a GPU-powered deterministic simulator capable of realizing both a fine-grained and a coarse-grained parallelization strategy.

The framework presented here was applied to a complex biological system of relapsing-remitting multiple sclerosis, consisting in 3200 reactions and 700 chemical species. In particular, we realized a parameter sweep analysis to investigate the effects of possible malfunctions in the Teff-Treg cross regulation mechanisms that involve a break of peripheral tolerance and bring to the occurrence of relapses. Thanks to the acceleration provided by LASSIE, we obtained around \(97\times \) speed-up with respect to a CPU-based execution of the same analysis.

As a future extension of this work, on the one hand, we plan to execute extensive analyses of the parameter space of the model to better understand the underlying mechanisms of multiple sclerosis; on the other hand, we will assess the performance of our framework on different GPUs and on multi-GPU systems.