Abstract
The very powerful Theorem 11.6.1 told us that, when a nondegenerate network’s Species-Reaction Graph satisfies certain mild conditions, behavior is severely constrained to be largely stable and dull, provided only that the kinetics associated with the network resides in the large and natural weakly monotonic class. The underlying idea was that, when those graphical conditions are satisfied, the network’s fully open extension is concordant. Nondegeneracy of the original network then ensured that it too is concordant, in which case the original network inherits all the dynamical attributes that concordance mandates.
This is a preview of subscription content, log in via an institution.
Buying options
Tax calculation will be finalised at checkout
Purchases are for personal use only
Learn about institutional subscriptionsNotes
- 1.
The same guide applies to the proof of the strong-concordance variant, Theorem 11.8.1.
- 2.
Recall that a degradation reaction is one of the form
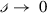 .
. - 3.
When we say that A is causal for B, we do not mean to suggest that A by itself determines the outcome B, only that A abets or contributes to B.
- 4.
In the event that there are signed degradation-like reactions such as
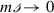 with m ≠ 1, then those too are omitted from the Sign-Causality Graph
with m ≠ 1, then those too are omitted from the Sign-Causality Graph - 5.
A directed graph is strongly connected if, for each choice of two vertices, those vertices are mutually reachable along directed paths. A strong component of a directed graph is a maximal strongly connected subgraph. A graph is nontrivial if it has an edge.
- 6.
It is easy to see that the stoichiometric coefficients
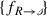 and
and 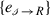 associated with edges in the oriented Species-Reaction Graph cycle are identical to their counterparts
associated with edges in the oriented Species-Reaction Graph cycle are identical to their counterparts 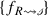 and
and 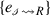 in the Sign-Causality Graph source cycle.
in the Sign-Causality Graph source cycle. - 7.
- 8.
As indicated earlier, the orientation is required to be consistent with directions carried by the fixed-direction edges of the Species-Reaction Graph.
- 9.
Here we are regarding the causal unit
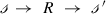 to reside in the Species-Reaction Graph rather in the Sign-Causality Graph.
to reside in the Species-Reaction Graph rather in the Sign-Causality Graph.
References
Biggs, N.: Algebraic Graph Theory. Cambridge University Press (1994)
Bondy, A., Murty, U.: Graph Theory. Springer, New York (2010)
Ellison, P., Ji, H., Knight, D., Feinberg, M.: The Chemical Reaction Network Toolbox, Version 2.3 (2014). Available at https://crnt.osu.edu
Gale, D.: The Theory of Linear Economic Models. University of Chicago Press, Chicago (1960)
Knight, D.: Reactor behavior and its relation to chemical reaction network structure. Ph.D. thesis, The Ohio State University (2015)
Knight, D., Shinar, G., Feinberg, M.: Sharper graph-theoretical conditions for the stabilization of complex reaction networks. Mathematical Biosciences 262(1), 10–27 (2015)
Shinar, G., Feinberg, M.: Concordant chemical reaction networks and the species-reaction graph. Mathematical Biosciences 241(1), 1–23 (2013)
Wilson, R.J.: Introduction to Graph Theory. Addison-Wesley, Reading, MA (1996)
Author information
Authors and Affiliations
Appendices
Appendix 19.A Proof of Proposition 19.12.3
Here we prove Proposition 19.12.3, repeated later in this appendix as Proposition 19.A.2.
Some additional vocabulary will lay the groundwork for a preliminary proposition. Let G be an oriented subgraph of the Species-Reaction Graph. Then G ∗⊂ G will be called an R-subgraph of G if it satisfies the first two of the requirements for a simple core but not necessarily the third. That is, G ∗ is an R-subgraph of G if G ∗ is strongly connected and, within G ∗, every reaction vertex is adjacent to precisely two species vertices. We say that G ∗ has an R-to-S ear in G if there exists in G a directed path that originates with a reaction vertex of G ∗ and terminates with a species vertex of G ∗ but contains no edge of G ∗.
The following is a precursor to the proof of Proposition 19.12.3.
Proposition 19.A.1 ( [118])
If G is a nontrivial strongly connected directed subgraph of the Species-Reaction Graph that has no simple core, then there exists in G an R-subgraph having an R-to-S ear in G.
Proof
We will show the existence of an R-subgraph with the desired R-to-S ear by means of an iterative construction. Because G is strongly connected, we know that it contains at least one R-subgraph—any directed cycle is an example—that we will designate G 0.
Now suppose that G
i is an R-subgraph of G, where i is a nonnegative integer index label that indicates the progress of our iteration. Because G has no simple core, G contains an edge that is not in G
i and that terminates at a species vertex of G
i. Let  be such an edge. Since G is strongly connected, there is a directed path P in G that originates at a vertex of G
i, is edge-disjoint from G
i, and terminates in R
∗. Let E be the union of P with the edge
be such an edge. Since G is strongly connected, there is a directed path P in G that originates at a vertex of G
i, is edge-disjoint from G
i, and terminates in R
∗. Let E be the union of P with the edge  . Note that E begins at a vertex of G
i, ends at the species vertex
. Note that E begins at a vertex of G
i, ends at the species vertex  , and has no edge in common with G
i. If the originating vertex of E is a reaction vertex of G
i, then G
i is the required R-subgraph, having E as its required R-to-S ear.
, and has no edge in common with G
i. If the originating vertex of E is a reaction vertex of G
i, then G
i is the required R-subgraph, having E as its required R-to-S ear.
If, instead, E originates at a species vertex of G
i, say  (which might be
(which might be  ), then E is either a path (when
), then E is either a path (when  ) or a cycle (when
) or a cycle (when  ), neither having an edge in common with G
i and whose only vertices in common with G
i are species vertices
), neither having an edge in common with G
i and whose only vertices in common with G
i are species vertices  and
and  .
.
In this case, let G i+1 = G i ∪ E, which is a still larger R-subgraph of G. The construction applied above to G i can be applied again to G i+i and then sequentially thereafter if necessary. Because G has no simple core, the process will end in an R-subgraph having the required R-to-S ear. □
We are now in a position to prove Proposition 19.12.3, which we repeat below as Proposition 19.A.2.
Proposition 19.A.2 ( [118])
If G is a nontrivial oriented strongly connected subgraph of the Species-Reaction Graph that has no simple core, then there exists in G a pair of directed cycles having as their intersection a single directed path originating at a species vertex and terminating at a reaction vertex.
Proof
Proposition 19.A.1 ensures the existence in G of an R-subgraph having an R-to-S ear. We denote by G
0 that R-subgraph and by E its R-to-S ear. Moreover, we denote by R
0 and  the reaction and species vertices at the ends of the ear. Because G
0 is strongly connected, G
0 contains within it a directed path P originating at R
0 and terminating at
the reaction and species vertices at the ends of the ear. Because G
0 is strongly connected, G
0 contains within it a directed path P originating at R
0 and terminating at  and also a directed path Q originating at
and also a directed path Q originating at  and terminating at R
0. In Figure 19.2 we show some possibilities.
and terminating at R
0. In Figure 19.2 we show some possibilities.
Because G
0 is an R-subgraph of G, the first vertex along the path P that is also a vertex of Q must be a species vertex (which might be  ). We denote that first vertex by
). We denote that first vertex by  . By
. By  we mean the segment of P beginning at R
0 and ending at
we mean the segment of P beginning at R
0 and ending at  .
.
From the definition of  , there can be no species vertex of
, there can be no species vertex of  that is also a vertex of Q (apart from
that is also a vertex of Q (apart from  ). Thus, there can be no internal vertices common to the path
). Thus, there can be no internal vertices common to the path  and the directed segment of Q (denoted
and the directed segment of Q (denoted  ) that begins at
) that begins at  and ends at R
0. Therefore, the union of the two paths,
and ends at R
0. Therefore, the union of the two paths,  , is a directed cycle, denoted C1.
, is a directed cycle, denoted C1.
Note that the union of the ear E and the path Q is also a directed cycle, which can also be viewed as the union of E with the two complementary Q-segments  and
and  . This second cycle,
. This second cycle,  , and the cycle C1 have as their intersection the single species-to-reaction path
, and the cycle C1 have as their intersection the single species-to-reaction path  . □
. □
Appendix 19.B Proof of Proposition 19.13.1
Our goal in this appendix is to prove Proposition 19.13.1, which we repeat below as Proposition 19.B.1.
Proposition 19.B.1 ([ 118,158 ])
Consider an oriented strongly connected subgraph G
∗
of the Species-Reaction Graph having species set
\({\mathcal {S}}_*\)
and reaction set
\({\mathcal {R}}_*\)
. Suppose that no directed cycle in G
∗
is stoichiometrically expansive and that, within G
∗
, every reaction vertex is adjacent to precisely two species vertices. Then there is a set of positive numbers
 that satisfies the following system of inequalities:
that satisfies the following system of inequalities:

The hypothesis requires each reaction vertex R to be adjacent to precisely two directed edges of G
∗, an edge incoming to R and an edge outgoing from R. For a particular R in (19.27), it should be understood that  and
and  are, respectively, those edges.
are, respectively, those edges.
Remark 19.B.2
Note that with each \(R \in {\mathcal {R}}_*\) we can associate a unique causal unit  in G
∗, and with each causal unit in G
∗ we can associate a unique R.Footnote 9 If we wish, then, we can regard G
∗ to be a directed strongly connected graph with vertices \({\mathcal {S}}_*\) and directed edge set \({\mathcal {U}}\) consisting of the causal units, one for each R. Note that, in such a graph, a pair of species might be joined by two different similarly directed edges,
in G
∗, and with each causal unit in G
∗ we can associate a unique R.Footnote 9 If we wish, then, we can regard G
∗ to be a directed strongly connected graph with vertices \({\mathcal {S}}_*\) and directed edge set \({\mathcal {U}}\) consisting of the causal units, one for each R. Note that, in such a graph, a pair of species might be joined by two different similarly directed edges,  and
and  , but this will cause no serious problems.
, but this will cause no serious problems.
Proof
As in Remark 19.B.2, we let \({\mathcal {U}}\) denote the set of causal units in G
∗. Our aim is to show the existence of positive numbers  that satisfy (19.B.1) or, equivalently,
that satisfy (19.B.1) or, equivalently,

To prepare for a vector reformulation of (19.B.2), let  be the standard basis for \({\mathbb {R}^{\mathcal {S_*}}}\), and let
be the standard basis for \({\mathbb {R}^{\mathcal {S_*}}}\), and let  be the standard basis for \({\mathbb {R}^{\mathcal {U}}}\). Now let \(T: {\mathbb {R}^{\mathcal {S_*}}} \to {\mathbb {R}^{\mathcal {U}}}\) be the linear transformation defined by
be the standard basis for \({\mathbb {R}^{\mathcal {U}}}\). Now let \(T: {\mathbb {R}^{\mathcal {S_*}}} \to {\mathbb {R}^{\mathcal {U}}}\) be the linear transformation defined by

and let \(z \in {\mathbb {R}^{\mathcal {U}}}\) be defined by

The existence of positive numbers  satisfying (19.B.2) is equivalent to the existence of \(q^* \in {\mathbb {R}^{\mathcal {S_*}}}\) satisfying
satisfying (19.B.2) is equivalent to the existence of \(q^* \in {\mathbb {R}^{\mathcal {S_*}}}\) satisfying
because then we can choose  to satisfy (19.B.2).
to satisfy (19.B.2).
From a theorem of Gale [87, p. 46], the existence of such a q ∗ is equivalent to the nonexistence of \(p \;\in \; \ker T^T \cap \;{\overline {\mathbb {R}}_+^{\mathcal {U}}}\) satisfying
where \(T^T: {\mathbb {R}^{\mathcal {U}}} \to {\mathbb {R}^{\mathcal {S_*}}}\) is the transpose of T, given by

To prove the nonexistence, we will say that \(c \in {\overline {\mathbb {R}}_+^{\mathcal {U}}}\) is a directed cycle vector if, in G
∗, there is a directed cycle such that  if
if  is a causal unit within the cycle and is zero otherwise. It is easy to see that every directed cycle vector is a member of \(\ker T^T \cap \;{\overline {\mathbb {R}}_+^{\mathcal {U}}}\). In fact, Lemma 19.B.3 below tells us more.
is a causal unit within the cycle and is zero otherwise. It is easy to see that every directed cycle vector is a member of \(\ker T^T \cap \;{\overline {\mathbb {R}}_+^{\mathcal {U}}}\). In fact, Lemma 19.B.3 below tells us more.
Lemma 19.B.3
Every nonzero member of \(\ker T^T \cap \;{\overline {\mathbb {R}}_+^{\mathcal {U}}}\) is a positive linear combination of directed cycle vectors.
Proof
A proof given in [158] is based on the idea that each positive vector in the pointed polyhedral cone \(\ker T^T \cap \;{\overline {\mathbb {R}}_+^{\mathcal {U}}}\) has a representation as a nonnegative combination of the cone’s extreme vectors. It is then argued that each nonzero extreme vector is a positive multiple of a directed cycle vector. A very different style of argument is essentially given in [24], where that book’s Proposition 7.14 is, apart from vocabulary, almost the same as Lemma 19.B.3. □
Now suppose that \(p \;\in \; \ker T^T \cap \;{\overline {\mathbb {R}}_+^{\mathcal {U}}}\) satisfies condition (19.B.6), and let
be a representation of p as a positive linear combination of directed cycle vectors. Then, from (19.B.6),
with all α θ positive. However, (19.B.9) is contradicted by the fact that each c θ ⋅ z is nonnegative, as we now argue:
Suppose that, for a particular θ, the directed cycle corresponding to c θ is

Then

with the last inequality coming from the fact that no directed cycle in G ∗ is stoichiometrically expansive.
This completes the proof of Proposition 19.B.1. □
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this chapter
Cite this chapter
Feinberg, M. (2019). Species-Reaction Graph Foundations. In: Foundations of Chemical Reaction Network Theory. Applied Mathematical Sciences, vol 202. Springer, Cham. https://doi.org/10.1007/978-3-030-03858-8_19
Download citation
DOI: https://doi.org/10.1007/978-3-030-03858-8_19
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-03857-1
Online ISBN: 978-3-030-03858-8
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)


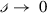 .
.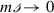 with m ≠ 1, then those too are omitted from the Sign-Causality Graph
with m ≠ 1, then those too are omitted from the Sign-Causality Graph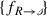 and
and 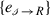 associated with edges in the oriented Species-Reaction Graph cycle are identical to their counterparts
associated with edges in the oriented Species-Reaction Graph cycle are identical to their counterparts 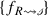 and
and 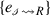 in the Sign-Causality Graph source cycle.
in the Sign-Causality Graph source cycle.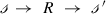 to reside in the Species-Reaction Graph rather in the Sign-Causality Graph.
to reside in the Species-Reaction Graph rather in the Sign-Causality Graph.