Abstract
In this chapter we’ll resume a narrative that ran through Chapters 7 and 8. There our interest was largely in the relationship between the structure of a reaction network and its capacity (or lack of it) to give rise to instabilities or multiple equilibria within a positive stoichiometric compatibility class. The principal theorems centered mostly on a reaction network’s deficiency or, in some cases, on the deficiencies of the network’s linkage classes. In this chapter, however, deficiencies will play almost no role at all.
This is a preview of subscription content, log in via an institution.
Buying options
Tax calculation will be finalised at checkout
Purchases are for personal use only
Learn about institutional subscriptionsChange history
02 February 2022
The original version of this book has been revised because it was inadvertently published with a few errors.
Notes
- 1.
The theorem does, however, refer to “nondegenerate networks,” defined and discussed in Section 10.6 of this chapter. The important thing to know is that degenerate networks, especially those that can admit a positive equilibrium, are highly pathological and rare. For example, no weakly reversible network is degenerate. Moreover, any degenerate network becomes nondegenerate when certain irreversible reactions are made reversible.
- 2.
- 3.
- 4.
In the classical situation, in which the rate constants for the effluent reactions are deemed to be the same positive number—see Section 4.2.1—any two equilibrium compositions will in fact be stoichiometrically compatible with respect to the stoichiometric subspace for the true chemistry, before the addition of inflow-outflow “reactions.” Unlike constraints considered in earlier chapters, this is not a stricture that needs to be imposed separately. Rather, it is a result that follows automatically from the governing differential equations.
- 5.
Inclusion of concordance tests began with the 2011 version of the Toolbox. For descriptions of concordance algorithms used, see [115, 117]. Definitive determinant tests for concordance [118] can be found in Remark 10.6.11. See also [177]. These are very similar to determinant tests for injectivity in mass action systems given earlier in [46, 49, 84].
- 6.
Determination of the concordance status of the three networks can be made with the Chemical Reaction Network Toolbox [62], which will also indicate that the fully open extensions of the three networks have the same concordance status as the originals.
- 7.
The species are numbered as in [122]. A species A 5 is not shown because it is presumed to be present in excess with largely time-invariant concentration. In the network displayed here, the reactions A 2 + A 4 → A 16 → A 2 + A 6 are intended to model the important stimulatory effect of A 2 (Dsh a) in an alternative route for the conversion of A 4 to A 6.
- 8.
Keep in mind that results about the existence of positive equilibria discussed in Remark 8.7.2 were restricted to mass action kinetics.
- 9.
Degeneracy of a network should not be confused with degeneracy of an equilibrium (Section 3.6). The latter is an attribute of a particular equilibrium composition for a given kinetic system. There is, however, a connection: for a degenerate network taken with any differentiably monotonic kinetics, every equilibrium is degenerate.
- 10.
In [49] it was argued that every weakly reversible network is normal, a network attribute that in turn implies network nondegeneracy.
- 11.
- 12.
When the stripping results in “reactions” such as 0 → 0 or, more generally, “reactions” of the form y → y, having the same reactant and product complexes, such “reactions” are simply omitted.
- 13.
- 14.
Strictly speaking, a map on a real vector space has only real eigenvalues. We are using “eigenvalue” here as a synonym for a root of the characteristic polynomial.
- 15.
As usual, we are referring here to eigenvalues associated with eigenvectors in the network’s stoichiometric subspace.
- 16.
- 17.
Recall from Lemma 3.5.2 that positively dependent reaction vectors are necessary for the existence of positive equilibrium.
- 18.
The construction of a complex balanced mass action kinetics and its consequences are related to the discussion in Section 7.7. We will have more to say about these things in Part III of this book.
- 19.
- 20.
For a vector \(x \in {\mathbb {R}^{\mathcal {S}}}\), we mean by sgn (x) the function from \({\mathcal {S}}\) to {−1, 0, 1} that assigns to each species
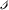 the sign of the number
the sign of the number 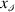 .
. - 21.
- 22.
See in particular Proposition 10.3 of [49].
- 23.
References
Aris, R.: Introduction to the Analysis of Chemical Reactors. Prentice-Hall, Inc., Englewood Cliffs, NJ (1965)
Arnold, V.I.: Ordinary Differential Equations. Springer, New York (1992)
Banaji, M., Craciun, G.: Graph-theoretic approaches to injectivity and multiple equilibria in systems of interacting elements. Communications in Mathematical Sciences 7(4), 867–900 (2009)
Banaji, M., Donnell, P., Baigent, S.: P-matrix properties, injectivity, and stability in chemical reaction systems. SIAM Journal on Applied Mathematics 67(6), 1523 (2007)
Craciun, G.: Systems of nonlinear differential equations deriving from complex chemical reaction networks. Ph.D. thesis, The Ohio State University (2002)
Craciun, G., Feinberg, M.: Multiple equilibria in complex chemical reaction networks. I. The injectivity property. SIAM Journal on Applied Mathematics 65(5), 1526–1546 (2005)
Craciun, G., Feinberg, M.: Multiple equilibria in complex chemical reaction networks: extensions to entrapped species models. IEE Proc. Syst. Biol 153(4), 179–186 (2006)
Craciun, G., Feinberg, M.: Multiple equilibria in complex chemical reaction networks. II. The species-reaction graph. SIAM Journal on Applied Mathematics 66(4), 1321–1338 (2006)
Craciun, G., Feinberg, M.: Multiple equilibria in complex chemical reaction networks: semi-open mass action systems. SIAM Journal on Applied Mathematics 70(6), 1859–1877 (2010)
Craciun, G., Tang, Y., Feinberg, M.: Understanding bistability in complex enzyme-driven reaction networks. Proceedings of the National Academy of Sciences 103(23), 8697–8702 (2006)
De Kepper, P., Boissonade, J.: Theoretical and experimental analysis of phase diagrams and related dynamical properties in the Belousov–Zhabotinskii system. The Journal of Chemical Physics 75(1), 189–195 (1981)
Ellison, P., Ji, H., Knight, D., Feinberg, M.: The Chemical Reaction Network Toolbox, Version 2.3 (2014). Available at crnt.osu.edu
Feinberg, M.: Lectures on Chemical Reaction Networks (1979). Written version of lectures given at the Mathematical Research Center, University of Wisconsin, Madison, WI Available at http://crnt.osu.edu/LecturesOnReactionNetworks
Feliu, E., Wiuf, C.: Preclusion of switch behavior in networks with mass-action kinetics. Applied Mathematics and Computation 219(4), 1449–1467 (2012)
Geiseler, W., Bar-Eli, K.: Bistability of the oxidation of cerous ions by bromate in a stirred flow reactor. The Journal of Physical Chemistry 85(7), 908–914 (1981)
Golubitsky, M., Langford, W.F.: Classification and unfoldings of degenerate Hopf bifurcations. Journal of Differential Equations 41(3), 375–415 (1981)
Golubitsky, M., Schaeffer, D.: Singularities and Groups in Bifurcation Theory: Volume I. Springer, New York (1984)
Graziani, K.R., Hudson, J.L., Schmitz, R.A.: The Belousov-Zhabotinskii reaction in a continuous flow reactor. The Chemical Engineering Journal 12(1), 9–21 (1976)
Guckenheimer, J., Holmes, P.: Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields. Springer, New York (2002)
Hirsch, M.W., Smale, S., Devaney, R.L.: Differential Equations, Dynamical Systems, and an Introduction to Chaos, Third Edition. Academic Press (2012)
Horn, F.: Necessary and sufficient conditions for complex balancing in chemical kinetics. Archive for Rational Mechanics and Analysis 49(3), 172–186 (1972)
Horn, F., Jackson, R.: General mass action kinetics. Archive for Rational Mechanics and Analysis 47(2), 81–116 (1972)
Hudson, J.L., Mankin, J.C.: Chaos in the Belousov - Zhabotinskii reaction. The Journal of Chemical Physics 74(11), 6171–6177 (1981)
Ji, H.: Uniqueness of equilibria for complex chemical reaction networks. Ph.D. thesis, The Ohio State University (2011)
Knight, D.: Reactor behavior and its relation to chemical reaction network structure. Ph.D. thesis, The Ohio State University (2015)
Knight, D., Shinar, G., Feinberg, M.: Sharper graph-theoretical conditions for the stabilization of complex reaction networks. Mathematical Biosciences 262(1), 10–27 (2015)
Lee, E., Salic, A., Krüger, R., Heinrich, R., Kirschner, M.W.: The roles of APC and axin derived from experimental and theoretical analysis of the Wnt pathway. PLoS Biology 1(1), e10 (2003)
Leib, T., Rumschitzki, D., Feinberg, M.: Multiple steady states in complex isothermal CFSTRs. I: General considerations. Chemical Engineering Science 43(2), 321–328 (1988)
Rawlings, J., Ekerdt, J.: Chemical Reactor Analysis and Design Fundamentals, 2nd edn. Nob Hill Publishing, Madison, Wisconsin (2013)
Reidl, J., Borowski, P., Sensse, A., Starke, J., Zapotocky, M., Eiswirth, M.: Model of calcium oscillations due to negative feedback in olfactory cilia. Biophysical Journal 90(4), 1147–1155 (2006)
Rumschitzki, D.: On the theory of multiple steady states in isothermal CSTR’s. Ph.D. thesis, University of California, Berkeley [Work performed at the University of Rochester] (1983)
Rumschitzki, D., Feinberg, M.: Multiple steady states in complex isothermal CFSTRs II. Homogeneous reactors. Chemical Engineering Science 43(2), 329–337 (1988)
Schlosser, P.M.: A graphical determination of the possibility of multiple steady states in complex isothermal CFSTRs. Ph.D. thesis, University of Rochester (1988)
Schlosser, P.M., Feinberg, M.: A theory of multiple steady states in isothermal homogeneous CFSTRs with many reactions. Chemical Engineering Science 49(11), 1749–1767 (1994)
Schmitz, R.A., Graziani, K.R., Hudson, J.L.: Experimental evidence of chaotic states in the Belousov-Zhabotinskii reaction. The Journal of Chemical Physics 67(7), 3040–3044 (1977)
Seydel, R.: Practical Bifurcation and Stability Analysis, 3rd edn. Springer, New York (2009)
Shinar, G., Feinberg, M.: Concordant chemical reaction networks. Mathematical Biosciences 240(2), 92–113 (2012)
Shinar, G., Feinberg, M.: Concordant chemical reaction networks and the species-reaction graph. Mathematical Biosciences 241(1), 1–23 (2013)
Strogatz, S.H.: Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering, Second Edition. Westview Press (2014)
Tyson, J., Kauffman, S.: Control of mitosis by a continuous biochemical oscillation: synchronization; spatially inhomogeneous oscillations. Journal of Mathematical Biology 1(4), 289–310 (1975)
Wiuf, C., Feliu, E.: Power-law kinetics and determinant criteria for the preclusion of multistationarity in networks of interacting species. SIAM Journal on Applied Dynamical Systems 12(4), 1685–1721 (2013)
Author information
Authors and Affiliations
Appendices
Appendix 10.A Deducing Behavior of a Reaction Network from What Is Known About Its Behavior in a Fully Open Context
The body of work alluded to in Section 10.2 was aimed at understanding the surprisingly dull behavior exhibited, over a very wide range of different chemistries, by (isothermal) classical continuous-flow stirred-tank reactors (CFSTRs). In their underlying arguments, these results relied heavily on the mathematical features of the fully open setting—features that are apt for classical CFSTRs but not broadly. In biological applications, for example, we should not expect that, for every species  , there will be a degradation reaction of the form
, there will be a degradation reaction of the form  .
.
When results derived in the fully open context are available, it is natural to wonder about the extent to which the fully open requirement can be relaxed. Stated differently, we would like to know when a statement that holds true for a network’s fully open extension, modified to account for stoichiometric compatibility, extends to the network itself. In this chapter there was considerable discussion of that very issue, but always in consideration of what can be said about a network’s behavior when it is known that the network’s fully open extension is concordant.
It is the purpose of this appendix to discuss, briefly and informally, certain results along these lines, results that transcend concordance considerations or even restrictions to particular classes of kinetics. For the sake of concretion, we will restrict our attention to information that derives from knowledge of the impossibility of multiple positive equilibria in a fully open setting.
It is reasonable to conjecture that, for a given chemistry, the impossibility of multiple positive equilibria in a fully open CFSTR context (including a feed stream) implies the impossibility of multiple positive stoichiometrically compatible equilibria for the chemistry itself, removed from the fully open setting. That conjecture, unmodified, would be false. Consider, for example, the pathological mass action system (10.A.1) considered earlier in Section 8.A.3. Recall that in each positive stoichiometric compatibility class there are multiple equilibria, in fact an infinite number of them. (See Figure 8.A.2.) Yet, it can be confirmed that, in a fully open CFSTR context, there is precisely one positive equilibrium, so long as there is some A in the feed stream.
The conjecture is, however, almost true. Implicit-function-theorem arguments in [47] indicate that if a reaction network, taken with a smooth kinetics, admits two distinct stoichiometrically compatible nondegenerate Footnote 21 positive equilibria, then there are parameter values for a classical CFSTR, within which the same kinetic system is operative, such that there are again two distinct positive equilibria. Therefore, a theorem that serves to deny the capacity for multiple positive equilibria in the fully open CFSTR context also gives information about the capacity for multiple stoichiometrically compatible positive equilibria for the original chemistry: There can be multiple stoichiometrically compatible positive equilibria for the original chemistry only if all but perhaps one of those equilibria are degenerate. Note that all positive equilibria of the mass action system (10.A.1) are degenerate.
Appendix 10.B Mass Action Injectivity
The principal theorems of this chapter circumscribe behavior for the very large class of concordant reaction networks when the kinetics is subject to very weak constraints (e.g., when the kinetics is differentiably monotonic). To a great extent, these theorems have significant roots in prior work restricted to mass action kinetics. In fact, some of the earlier theory tailored specifically to mass action systems permit similar theorems for a still broader class of networks, including some discordant ones. It is the purpose of this appendix to illuminate, briefly, some relationships between results in this chapter and results that derive from earlier mass-action-specific theory.
1.1 10.B.1 Two Similar Theorems, One Broad and One Mass-Action-Specific
By way of example, we will state two theorems—Theorems 10.B.2 and 10.B.3—one very general in the kinetics it invokes and one specific to mass action kinetics. Once these are in place, we will be in a position to consider an example that indicates how mass-action-restricted theorems can give information when broader theorems are silent.
As a precursor to the statement of Theorem 10.B.2, we recall Theorem 10.5.15, repeated below as Theorem 10.B.1. (See Section 10.B.3.1 for remarks about the proof.)
Theorem 10.B.1
For reaction network \({\{\mathcal {S},\mathcal {C},\mathcal {R}\}}\) the following are equivalent:
-
(i)
\({\{\mathcal {S},\mathcal {C},\mathcal {R}\}}\) is concordant
-
(ii)
For every choice of a differentiably monotonic kinetics \({\mathcal {K}}\) the derivative of the species-formation-rate function for the kinetic system \({\{\mathcal {S},\mathcal {C},\mathcal {R},\mathcal {K}\}}\) is nonsingular at every positive composition.
Items (i) and (ii) in Theorem 10.B.1 are then equivalent to item (ii) in Theorem 10.5.5 and item (iii) in Proposition 10.5.8. For the purposes of this appendix, the important equivalence is the one expressed in the following theorem, which is merely a corollary of Theorems 10.B.1 and 10.5.5:
Theorem 10.B.2
For reaction network \({\{\mathcal {S},\mathcal {C},\mathcal {R}\}}\) the following are equivalent:
-
(i)
For every weakly monotonic kinetics \({\mathcal {K}}\) the kinetic system \({\{\mathcal {S},\mathcal {C},\mathcal {R},\mathcal {K}\}}\) is injective.
-
(ii)
For every choice of a differentiably monotonic kinetics \({\mathcal {K}}\) the derivative of the species-formation-rate function for the kinetic system \({\{\mathcal {S},\mathcal {C},\mathcal {R},\mathcal {K}\}}\) is nonsingular at every positive composition.
In preparation for the statement of a mass action version of Theorem 10.B.2, we will want to qualify the meaning of kinetic-system injectivity just slightly. Recall that a kinetic system is injective if its species-formation-rate function f(⋅) has the property that f(c ∗) ≠ f(c ∗∗) whenever c ∗ and c ∗∗ are distinct stoichiometrically compatible compositions, at least one of which is positive. We shall say that a kinetic system is positive-composition injective if f(c ∗) ≠ f(c ∗∗) whenever c ∗ and c ∗∗ are distinct stoichiometrically compatible compositions, both positive.
Proof of the following theorem is given in Section 10.B.3.2. See also Remark 10.B.4.
Theorem 10.B.3
For reaction network \({\{\mathcal {S},\mathcal {C},\mathcal {R}\}}\) the following are equivalent:
-
(i)
For every choice of rate constants \(k \in {\mathbb {R}_+^{\mathcal {R}}}\) the mass action system \({\{\mathcal {S},\mathcal {C},\mathcal {R},k\}}\) is positive-composition injective.
-
(ii)
For every choice of rate constants \(k \in {\mathbb {R}_+^{\mathcal {R}}}\) the derivative of the species-formation-rate function for the mass action system \({\{\mathcal {S},\mathcal {C},\mathcal {R},k\}}\) is nonsingular at every positive composition.
If a network satisfies either of the two equivalent conditions in Theorem 10.B.3, we will say that the network is mass action injective. For a network of interest, condition (ii) provides an attractive route to a computational test for mass action injectivity. Such a test is available in [62]. Computational aspects are discussed later in Section 10.B.4 and more fully in [115].
In fact, the two equivalences given by Theorems 10.B.2 and 10.B.3 have computational virtues: in both cases they tie difficult-to-study global properties in (i) of the nonlinear species-formation-rate function \(f: {\overline {\mathbb {R}}_+^{\mathcal {S}}} \to S\) directly to properties in (ii) of a more local object, the linear transformation df(c) : S → S.
Remark 10.B.4
Theorem 10.B.3 has origins in the Ph.D. thesis of Gheorghe Craciun [44], which focused on fully open reaction networks. For the fully open case, proofs appeared there and in [46], along with determinant-based theorems for assessing injectivity of fully open mass action systems. These in turn provided foundations for Species-Reaction Graph mass action theorems given in [47] and [52].
For networks that are not fully open, stoichiometric considerations exert themselves, and the proof becomes slightly more complicated. For this more general case, Theorem 10.B.3 was stated in Remark 6.4 of [49], where determinant conditions for mass action injectivity were again provided, this time for networks that are not presumed to be fully open.Footnote 22 For the purpose of documenting the mass-action-injectivity computational module of [62], a proof of Theorem 10.B.3—essentially the one given in Section 10.B.3.2—was included in the Ph.D. thesis of Haixia Ji [115]. A proof was also given [84], where a determinant-based Mathematica-like script for assessment of mass action injectivity was provided.
1.2 10.B.2 Two Instructive Examples
In this section we examine two networks that teach very different lessons.
Example 10.B.5
Consider first network (10.B.2).

The network is discordant, as can be determined by means of [62]. Theorem 10.5.5 then tells us that there is a weakly monotonic kinetics for the network such that the resulting kinetic system is not injective. In fact, Theorem 10.5.10 tells us more: there is for the network a weakly monotonic kinetics for which the resulting kinetic system admits a pair of distinct positive stoichiometrically compatible equilibria. Moreover, Theorem 10.B.1 ensures for the network the existence of a differentiably monotonic kinetics such that at some positive composition the derivative of the species-formation-rate function is singular. In particular, Theorem 10.7.7 tells us that the kinetics can be chosen in such a way as to engender a degenerate positive equilibrium.
On the other hand, the network is mass action injective; this too can be determined by means of [62]. Theorem 10.B.3 then tells us that, while there is indeed some kinetics for the network that give rise to the various phenomena just described, there is no mass action kinetics for which these phenomena will be admitted, no matter what rate constants are assigned to the various reactions.Footnote 23
The example demonstrates concretely that, for at least certain networks, the equivalent behavior-restricting conditions in the mass action Theorem 10.B.3 might be satisfied, while those in the more kinetically expansive Theorem 10.B.2 are not. Indeed, theory focused exclusively on the archetypal mass action kinetics has a special richness all its own.
Example 10.B.6
There is a possible source of confusion that we would do well to mitigate by means of an example. Recall network (10.B.3), which we met earlier in Section 10.4.
The network is not concordant, nor is it mass action injective [62]. In particular, neither of the two equivalent conditions in Theorem 10.B.3 is satisfied. This tells us that there is a rate constant specification such that the resulting mass action system admits a pair of stoichiometrically compatible positive compositions, c ∗ and c ∗∗, at which the species-formation-rate function takes identical values: f(c ∗) = f(c ∗∗). Moreover, there is a (perhaps different) rate constant specification such that at some positive composition, the derivative of the species-formation-rate function has a singular derivative.
Note, however, that network (10.B.3) has a deficiency of zero (n = 6, ℓ = 3, s = 3).
The Deficiency Zero Theorem (Theorem 7.1.1) tells us that for no assignment of rate constants can the resulting mass action system admit a pair of stoichiometrically compatible positive equilibria. This is to say that, although for some rate constant assignment the species-formation-rate function can indeed take the same value at two different stoichiometrically compatible positive compositions, that value cannot be zero.
Moreover, the local version of the Deficiency Zero Theorem (Theorem 7.3.1 ) tells us that for no assignment of rate constants can there be a positive equilibrium that is degenerate. This is to say that, although for some rate constant assignment there can be a positive composition at which the derivative of species-formation-rate function is singular, that composition cannot be an equilibrium.
The lesson here is this: Although mass action injectivity is a network attribute that does indeed preclude multiple stoichiometrically compatible positive equilibria and degenerate positive equilibria, regardless of rate constant values, the same preclusions might result even for networks that are not mass action injective.
1.3 10.B.3 Some Proofs
In this section we provide proofs of Theorems 10.B.1 and 10.B.3.
1.3.1 10.B.3.1 Proof of Theorem 10.B.1
The implication (i) ⇒ (ii) is the subject of Theorem 10.5.14, which was proved in [157]. Proof that (ii) ⇒ (i) is essentially contained in the proof of Theorem 10.7.7, also given in [157]; we provide the relevant part of that argument below. (Theorem 10.7.7 more or less gives what we want here, but its emphasis is on the stability of positive equilibria.)
Proof ((ii)⇒ (i))
Suppose that (ii) holds but that the network is discordant. In this case, Proposition 10.6.25 tells us that we can choose \(\{p_{{y \to y'}}\}_{{y \to y'} \in {\mathcal {R}}} \subset {\overline {\mathbb {R}}_+^{\mathcal {S}}}\), with \({\mathrm {supp} \,} p_{{y \to y'}} = {\mathrm {supp} \,} y\), \(\forall \mbox{{$y \to y'$}} \in {\mathcal {R}}\), such that the linear transformation T : S → S given by
is singular. Now let \(c^* \in {\overline {\mathbb {R}}_+^{\mathcal {S}}}\) be some fixed positive composition, and for the network \({\{\mathcal {S},\mathcal {C},\mathcal {R}\}}\) let \({\mathcal {K}}\) be the kinetics defined, for each \({y \to y'} \in {\mathcal {R}}\), by
where
For this choice, the derivative at c ∗ of the species-formation-rate function for the differentiably monotonic kinetic system \({\{\mathcal {S},\mathcal {C},\mathcal {R},\mathcal {K}\}}\) coincides with the singular linear transformation T : S → S given by (10.B.4). This contradicts (ii). □
1.3.2 10.B.3.2 Proof of Theorem 10.B.3
Recall from Remark 3.6.2 that, for a mass action system \({\{\mathcal {S},\mathcal {C},\mathcal {R},k\}}\) with stoichiometric subspace S, the derivative of the species-formation-rate function f(⋅) has a special form: At composition \(a \in {\mathbb {R}_+^{\mathcal {S}}}\) the derivative df(a) : S → S is given by the requirement that, for each σ ∈ S,
where, for each \({y \to y'} \in {\mathcal {R}}\),
and “∗a” indicates the scalar product in \({\mathbb {R}^{\mathcal {S}}}\) defined by

With this in mind, we can restate Theorem 10.B.3 in the following way, essentially asserting, in more detail, the equivalence of the negations of (i) and (ii) in the original statement.
Theorem 10.B.7 ( [49, 115])
For reaction network \({\{\mathcal {S},\mathcal {C},\mathcal {R}\}}\) with stoichiometric subspace S the following are equivalent:
-
(i)
There is a choice of rate constants \(k \in {\mathbb {R}_+^{\mathcal {R}}}\) and two distinct positive compositions c ∗ and c ∗∗ , with c ∗− c ∗∗∈ S, such that
$$\displaystyle \begin{aligned} \sum_{y \to y' \in \mathcal{R}}k_{y \to y'}(c^*)^y(y'-y) = \sum_{y \to y' \in \mathcal{R}}k_{y \to y'}(c^{**})^y(y'-y). \end{aligned} $$(10.B.10) -
(ii)
There is a choice of \(\eta \in {\mathbb {R}_+^{\mathcal {R}}}\) and \(a \in {\mathbb {R}_+^{\mathcal {S}}}\) such that the linear transformation T η,a : S → S given by
$$\displaystyle \begin{aligned} T_{\eta,\,a}\sigma\; := \sum_{{y \to y'}\ \in\ {\mathcal{R}}}\eta_{{y \to y'}}(y*_{a}\sigma)(y' - y) \end{aligned} $$(10.B.11)is singular.
Proof
(i) ⇒ (ii): With k, c ∗, and c ∗∗ as in (i), we can rewrite (10.B.10) in the following form:
where “⋅” is the standard scalar product in \({\mathbb {R}^{\mathcal {S}}}\) and
Now let
Note that, componentwise, sgn μ = sgn σ. Therefore, there is an \(a \in {\mathbb {R}_+^{\mathcal {S}}}\) such that \(\mu = \frac {1}{a}\sigma \). Then, in (10.B.12), we can replace y ⋅ μ by y ∗a σ, where “∗a” is the scalar product in \({\mathbb {R}^{\mathcal {S}}}\) given by (10.B.9).
Note also that \({\mathrm {sgn} \,}(e^{y*_a\sigma }- 1) = {\mathrm {sgn} \,}(y*_a\sigma )\). Thus, for each \(y \in {\mathcal {C}}\), there is a positive number p y such that \(e^{y*_a\sigma }- 1 = p_y(y*_a\sigma )\). If, for each \({y \to y'} \in {\mathcal {R}}\), we set \(\eta _{y\to y'} := k_{y \to y'}(c^*)^yp_y\), it follows from (10.B.12) that
Because σ is not zero, it follows from (10.B.15) that the linear transformation T η,a : S → S defined in (ii) is singular.
(ii) ⇒ (i): Suppose that \(\eta \in {\mathbb {R}_+^{\mathcal {R}}}\), \(a \in {\mathbb {R}_+^{\mathcal {S}}}\), and nonzero σ ∈ S are such as to make (10.B.15) true. Let
in which case (10.B.15) becomes
Because sgn (y ⋅ μ) = sgn (e y⋅μ − 1), it is not difficult to see that we can choose \(\bar {\eta } \in {\mathbb {R}_+^{\mathcal {R}}}\) such that
Because, componentwise, sgn (μ) = sgn (σ), we also have sgn (e μ − 1) = sgn σ. Thus, there is c ∗∈ \({\mathbb {R}_+^{\mathcal {S}}}\) such that σ = c ∗(e μ − 1). Now let c ∗∗ := c ∗ e μ. Note that c ∗∗≠ c ∗, c ∗∗− c ∗ = σ ∈ S, and \(\mu = \ln c^{**} - \ln c^*\). After choosing k ∈ \({\mathbb {R}_+^{\mathcal {R}}}\) to satisfy \(\bar {\eta }_{y\to y'} = k_{y \to y'}(c^*)^y, \forall \, y \to y' \in \mathcal {R}\), we can begin with (10.B.18) and then reverse the steps in (10.B.12) to obtain (10.B.15). □
1.4 10.B.4 A Route to the Determination of Mass Action Injectivity
Condition (ii) of Theorem 10.B.7 suggests several routes to establishing that a given network is or is not mass action injective. In particular, it is easy to see that (ii) is equivalent to the following:
(iii) There is a choice of \(\eta \in {\mathbb {R}_+^{\mathcal {R}}}\) such that the linear transformation \(\bar {T}_{\eta }:{\mathbb {R}^{\mathcal {S}}} \to S\) given by
has in its kernel a vector that is sign-compatible with S.
Here “⋅” denotes the standard scalar product in \({\mathbb {R}^{\mathcal {S}}}\). Recall that a vector \(\gamma ^{*} \in {\mathbb {R}^{\mathcal {S}}}\) is sign-compatible with S (Definition 8.5.1) if there exists σ ∈ S such that, componentwise, sgn γ ∗ = sgn σ. This formulation permits a connection with the linear transformation \(L:{\mathbb {R}^{\mathcal {R}}} \to S\), given by
the linear transformation that appears in the definition of concordance. Clearly, (iii) is equivalent to the following:
(iv) There exist \(\alpha \in \ker L\) and a nonzero \(\gamma \in {\mathbb {R}^{\mathcal {S}}}\), sign-compatible with S, such that \({\mathrm {sgn} \,}(y \cdot \gamma ) = {\mathrm {sgn} \,} \alpha _{{y \to y'}}\) for all \({y \to y'} \in {\mathcal {R}}\).
Mass action injectivity (or lack of it) can be determined—as it is in [62]—by means of sign-checking along lines described in (iv). For algorithmic aspects see [115].
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this chapter
Cite this chapter
Feinberg, M. (2019). Concordant Reaction Networks: Architectures That Promote Dull, Reliable Behavior Across Broad Kinetic Classes. In: Foundations of Chemical Reaction Network Theory. Applied Mathematical Sciences, vol 202. Springer, Cham. https://doi.org/10.1007/978-3-030-03858-8_10
Download citation
DOI: https://doi.org/10.1007/978-3-030-03858-8_10
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-03857-1
Online ISBN: 978-3-030-03858-8
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)


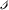 the sign of the number
the sign of the number 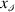 .
.