Abstract
We propose the first identity-based encryption (IBE) scheme that is (almost) tightly secure against chosen-ciphertext attacks. Our scheme is efficient, in the sense that its ciphertext overhead is only seven group elements, three group elements more than that of the state-of-the-art passively (almost) tightly secure IBE scheme. Our scheme is secure in a multi-challenge setting, i.e., in face of an arbitrary number of challenge ciphertexts. The security of our scheme is based upon the standard symmetric external Diffie-Hellman assumption in pairing-friendly groups, but we also consider (less efficient) generalizations under weaker assumptions.
You have full access to this open access chapter, Download conference paper PDF
1 Introduction
Tight Security. Usually, security reductions are used to argue the security of a cryptographic scheme \(S\). A reduction reduces any attack on \(S\) to an attack on a suitable computational problem \(P\). More specifically, a reduction constructs a successful \(P\)-solver  out of any given successful adversary
out of any given successful adversary  on \(S\). Intuitively, a reduction thus shows that \(S\) is at least as hard to break/solve as \(P\).
on \(S\). Intuitively, a reduction thus shows that \(S\) is at least as hard to break/solve as \(P\).
Ideally, we would like a reduction to be tight, in the sense that the constructed  has the same complexity and success probability as the given
has the same complexity and success probability as the given  . A tight security reduction implies that the security of \(S\) is tightly coupled with the hardness of \(P\). From a more practical perspective, a tight security reduction allows for more efficient parameter choices for \(S\), when deriving those parameters from the best known attacks on \(P\).
. A tight security reduction implies that the security of \(S\) is tightly coupled with the hardness of \(P\). From a more practical perspective, a tight security reduction allows for more efficient parameter choices for \(S\), when deriving those parameters from the best known attacks on \(P\).
Current State of the Art. Tight reductions have been studied for a variety of cryptographic primitives, such as public-key encryption [6, 17, 27,28,29, 37, 38], signature schemes [1, 2, 4, 8, 10, 12, 13, 18, 27, 29, 32, 37, 43], identity-based encryption (IBE) [3, 8, 11, 12, 21, 22, 31], non-interactive zero-knowledge proofs [17, 29, 37], and key exchange [5, 26].
Existing tight reductions and corresponding schemes differ in the type and quality of tightness, and in the incurred cost of tightness. For instance, most of the referenced works provide only what is usually called “almost tight” reductions. In an almost tight reduction, the success probability of  may be smaller than
may be smaller than  , but only by a factor depends only on the security parameter (but not, e.g., on the size of
, but only by a factor depends only on the security parameter (but not, e.g., on the size of  ). Furthermore, some reductions consider the scheme only in a somewhat restricted setting, such as an IBE setting in which only one challenge ciphertext is considered.
). Furthermore, some reductions consider the scheme only in a somewhat restricted setting, such as an IBE setting in which only one challenge ciphertext is considered.
Our Goal: (Almost) Tightly CCA-Secure IBE Schemes in the Multi-challenge Setting. In this work, we are interested in (almost) tight reductions for IBE schemes. As remarked above, there already exist a variety of (almost) tightly secure IBE schemes. However, most of these schemes only provide security of one challenge ciphertext, and none of them provide security against chosen-ciphertext attacks. Security of many challenge ciphertexts is of course a more realistic notion; and while this notion is polynomially equivalent to the one-challenge notion, the corresponding reduction is far from tight, and defeats the purpose of tight security of the overall scheme in a realistic setting. Furthermore, chosen-ciphertext security guarantees security even against active adversaries [42].
On the Difficulty of Achieving Our Goal. Achieving many-challenge IBE security and chosen-ciphertext security appears to be technically challenging. First, with the exception of [21, 22], all known IBE constructions that achieve (almost) tight many-challenge security rely on composite-order groups, and are thus comparatively inefficient. The exception [22] (like its predecessor [21]) constructs an efficient (almost) tightly secure IBE scheme in the many-challenge setting by adapting and implementing the “(extended) nested dual system groups” framework [12, 31] in prime-order groups. Since this work is closest to ours, we will take a closer look at it after we have described our technical contribution. We stress, however, that also [22] does not achieve chosen-ciphertext security.
Second, canonical approaches to obtain chosen-ciphertext security do not appear to apply to existing tightly secure IBE schemes. For instance, it is known that hierarchical identity-based encryption (HIBE) implies chosen-ciphertext secure IBE [9]. However, currently no tightly secure HIBE schemes are known, and in fact there are lower bounds on the quality of (a large class of) security reductions for HIBE schemes [36].
Another natural approach to achieve chosen-ciphertext security is to equip ciphertexts with a non-interactive zero-knowledge (NIZK) proof of knowledge of the corresponding plaintext. Intuitively, a security reduction can use this NIZK proof to extract the plaintext message from any adversarially generated decryption query. Highly optimized variants of this outline are responsible for highly efficient public-key encryption schemes (e.g., [14, 15, 35, 41]).
 (for symmetric pairings),
(for symmetric pairings),  , and
, and  . \(|\mathsf {pk}|\) denotes the size of the (master) public key, and \(|\mathsf {C}|\) denotes the ciphertext overhead (on top of the message size).‘MC’ denotes many-challenge security, and ‘CCA’ chosen-ciphertext security. ‘Loss’ denotes the reduction loss, and ‘Assump.’ the assumption reduced to.
. \(|\mathsf {pk}|\) denotes the size of the (master) public key, and \(|\mathsf {C}|\) denotes the ciphertext overhead (on top of the message size).‘MC’ denotes many-challenge security, and ‘CCA’ chosen-ciphertext security. ‘Loss’ denotes the reduction loss, and ‘Assump.’ the assumption reduced to.  is a universal one-way hash function and \(|\mathsf H|\) denotes the size of the representation of \(\mathsf H\). \(|\mathsf {CH}|\) is the size of the hash key of a chameleon hash
is a universal one-way hash function and \(|\mathsf H|\) denotes the size of the representation of \(\mathsf H\). \(|\mathsf {CH}|\) is the size of the hash key of a chameleon hash  and
and  is the size of its randomness.
is the size of its randomness.It is plausible that this approach can be used to turn, e.g., the tightly secure schemes of [21, 22] into chosen-ciphertext secure schemes. However, this requires a NIZK proof system which is tightly secure and sound even in the presence of many simulated proofs. While such proof systems are constructible by combining Groth-Sahai proofs [24] with a tightly secure structure-preserving signature scheme [18] (see also [23, 29]), the resulting NIZK and IBE schemes would not be very efficient. In fact, efficient suitable NIZK schemes are only known for simple languages [17], which do not appear compatible with the complex IBE schemes of [21, 22].
Our Results. We provide a tightly chosen-ciphertext secure IBE scheme in the multi-challenge setting. Our scheme builds upon a new tightly chosen-plaintext secure IBE scheme whose efficiency is comparable with that of the state-of-the-art scheme of [22]. However, unlike [22], our scheme is compatible with the highly efficient NIZK proof system of [17]. This allows to upgrade our scheme to chosen-ciphertext security by adding an efficient consistency proof (that consists of only three group elements) to ciphertexts. We briefly remark that, similar to previous schemes [3, 8, 21, 22], our scheme also achieves a (somewhat weak) form of anonymity. We compare the efficiency of our scheme with existing state-of-the-art schemes in Table 1.
1.1 Technical Overview
The Approach of Blazy, Kiltz, and Pan (BKP). Our starting point is the MAC\(\rightarrow \)IBE transformation of Blazy, Kiltz, and Pan (BKP) [8], which in turn abstracts the IBE construction of Chen and Wee [12], and generalizes the PRF\(\rightarrow \)signatures transformation of Bellare and Goldwasser [7]. The BKP transformation assumes an “affine message authentication code” (affine MAC), i.e., a MAC in which verification consists in checking a system of affine equations. The variables in these affine equations comprise the MAC secret key, and the (public) coefficients are derived from the message to be signed.
This affine MAC is turned into an IBE scheme as follows: the IBE master public key \(\mathsf {pk}=\mathsf {Com}(\mathsf {K})\) consists of a commitment to the MAC secret key \(\mathsf {K}\). An IBE user secret key \(\mathsf {usk}[\mathsf {id}]\) for an identity \(\mathsf {id}\) consists of a MAC tag \(\tau _{\mathsf {id}}\) on the message \(\mathsf {id}\), along with a NIZK proof that \(\tau _{\mathsf {id}}\) indeed verifies correctly relative to \(\mathsf {pk}\). The key observation of BKP is now that we can implement commitments and NIZK proof using the Groth-Sahai proof system [24]. Since the used MAC is affine, the corresponding verification involves only linear equations, which makes the corresponding proofs rerandomizable.
Now an IBE ciphertext \(C\) essentially contains a rerandomized version of the public, say, left-hand side of the NIZK equations for verifying the validity of \(\tau _{\mathsf {id}}\). The corresponding right-hand side can be computed either from the randomization information (known to the sender), or using the NIZK proof for \(\tau _{\mathsf {id}}\) (known to the receiver through \(\mathsf {usk}[\mathsf {id}]\)). Of course, this technique relies on subtleties of the Groth-Sahai proof system that our high-level overview cannot cover.
Advantages and Limitations of the BKP Approach. The BKP approach has the nice property that the (one-challenge, chosen-plaintext) security of the resulting IBE scheme can be tightly reduced to the (one-challenge) security of the MAC scheme. In particular, BKP also gave a MAC scheme which is tightly secure in a one-challenge setting under a standard computational assumption. At the same time, BKP only consider one IBE challenge ciphertext, and chosen-plaintext security. In particular in large-scale scenarios with huge amounts of ciphertexts and active adversaries, this again defeats the purpose of a tight reduction.
First Modification: Achieving Many-Challenge Security. We will first show that the BKP reduction can be easily extended to the many-challenge case, assuming of course that the underlying MAC scheme is secure in the many-challenge setting. In this, the actual difficulty lies in constructing a suitable MAC scheme. We do so by adapting the affine MAC \(\mathsf {MAC}_{\mathsf {BKP}}\) of BKP, using ideas from the recent (almost) tightly secure PKE scheme of Gay et al. [17].
More specifically, \(\mathsf {MAC}_{\mathsf {BKP}}\) operates in a group  of order \(q\). We use the implicit notation \([x]:=g^x\) for group elements. \(\mathsf {MAC}_{\mathsf {BKP}}\) assumes a public matrix
of order \(q\). We use the implicit notation \([x]:=g^x\) for group elements. \(\mathsf {MAC}_{\mathsf {BKP}}\) assumes a public matrix  of a dimension \(n\) that depends on the underlying computational assumption. Its secret key is of the form
of a dimension \(n\) that depends on the underlying computational assumption. Its secret key is of the form
and a tag for a message \(\mathsf {m}\in \{0,1\}^\ell \) is of the form

Verification checks that \(u\) is of the form from (1).
We sketch now a bit more specifically how \(\mathsf {MAC}_{\mathsf {BKP}}\)’s security proof proceeds, assuming an adversary  in the EUF-CMA security game. The overall strategy is to gradually randomize all \(u\) values issued in
in the EUF-CMA security game. The overall strategy is to gradually randomize all \(u\) values issued in  ’s tag queries. This is equivalent to using different and independent “virtual” secret keys for each message. Hence, once this is done,
’s tag queries. This is equivalent to using different and independent “virtual” secret keys for each message. Hence, once this is done,  cannot be successful by an information-theoretic argument.
cannot be successful by an information-theoretic argument.
The main difficulty in randomizing all \(u\) is that a reduction must be able to still evaluate  ’s success in forging a tag for fresh message. In particular, the reduction must be able to compute \(u^*=\sum \mathbf {{x}}_{i,\mathsf {m}^*_i}^\top \mathbf {{t}}^*+x_0'\) for a message \(\mathsf {m}^*\) and value \(\mathbf {{t}}^*\) adaptively selected by
’s success in forging a tag for fresh message. In particular, the reduction must be able to compute \(u^*=\sum \mathbf {{x}}_{i,\mathsf {m}^*_i}^\top \mathbf {{t}}^*+x_0'\) for a message \(\mathsf {m}^*\) and value \(\mathbf {{t}}^*\) adaptively selected by  . The solution chosen by BKP, following Chen and Wee [12], is to iterate over all bit indices \(i\). For each \(i\), the reduction guesses the \(i\)-th bit \(\mathsf {m}^*_i\) of
. The solution chosen by BKP, following Chen and Wee [12], is to iterate over all bit indices \(i\). For each \(i\), the reduction guesses the \(i\)-th bit \(\mathsf {m}^*_i\) of  ’s forgery message, and embeds a computational challenge into \(\mathbf {{x}}_{i,1-\mathsf {m}^*_i}\). This allows to randomize all \(u\) in issued tags with \(\mathsf {m}_i\ne \mathsf {m}^*_i\), and still be able to evaluate \(u^*\). The corresponding reduction loses a multiplicative factor of only \(O(\ell )\). However, note that this strategy would not work with multiple challenges (i.e., potential forgeries \((\mathsf {m}^*,\tau ^*)\)) from
’s forgery message, and embeds a computational challenge into \(\mathbf {{x}}_{i,1-\mathsf {m}^*_i}\). This allows to randomize all \(u\) in issued tags with \(\mathsf {m}_i\ne \mathsf {m}^*_i\), and still be able to evaluate \(u^*\). The corresponding reduction loses a multiplicative factor of only \(O(\ell )\). However, note that this strategy would not work with multiple challenges (i.e., potential forgeries \((\mathsf {m}^*,\tau ^*)\)) from  . For instance, the simulation above is always only able to verify a given \(\tau ^*\) for exactly one of the two messages \(\mathsf {m}^*_0=0^\ell \) and \(\mathsf {m}^*_1=1^\ell \).
. For instance, the simulation above is always only able to verify a given \(\tau ^*\) for exactly one of the two messages \(\mathsf {m}^*_0=0^\ell \) and \(\mathsf {m}^*_1=1^\ell \).
Our solution here is to instead employ the randomization strategy used by Gay et al. [17] in the context of public-key encryption. Namely, we first increase the dimension of \(\mathbf {{x}}\). This allows us to essentially randomize both tags for messages with \(\mathsf {m}_i=0\) and \(\mathsf {m}_i=1\) simultaneously, using different parts of the \(\mathbf {{x}}_{i,b}\) independently. In particular, we will embed computational challenges in different parts of both \(\mathbf {{x}}_{i,0}\) and \(\mathbf {{x}}_{i,1}\). This allows to adapt the argument of Gay et al. to the case of MACs, and hence to prove a slight variant of the BKP MAC secure even under many-challenge attacks.
Second Modification: Achieving Chosen-Ciphertext Security. So far, we could almost completely follow the BKP approach, with only a slight twist to the BKP MAC, and by adapting the proof strategy of Gay et al. However, the resulting scheme is still not chosen-ciphertext secure. To achieve chosen-ciphertext security, we will follow one of the generic approaches outlined above. In this, the modular structure of the BKP IBE, and the simplicity of the used MAC will pay off.
More concretely, following Naor and Yung [41], we will add a NIZK proof to each ciphertext. Unlike in the generic paradigm of achieving chosen-ciphertext security via NIZK proofs, we do not explicitly prove knowledge of the corresponding plaintext. Instead, following Cramer and Shoup [14, 15], we prove only consistency of the ciphertext, in the sense that the ciphertext is a possible output of the encryption algorithm. Compared to a NIZK proof of knowledge (of plaintext), this yields a much more efficient scheme, but also requires more subtle proof of security.
Our security argument is reminiscent of that of Cramer and Shoup, but of course adapted to the IBE setting. Our reduction will be able to generate user decryption keys for all identities. These decryption keys will function perfectly well on consistent (in the above sense) ciphertexts at all times in the proof, but their action on inconsistent ciphertexts will be gradually randomized. Hence, adversarial decryption queries, whose consistency is guaranteed by the attached NIZK proof, will be decrypted correctly at all times. On the other hand, all generated challenge ciphertexts will be made inconsistent and will be equipped with simulated NIZK proofs early on.
Unlike Cramer and Shoup, who considered only one challenge ciphertext (for a PKE scheme), we need a very powerful NIZK scheme which enjoys (almost) tight unbounded simulation-soundness. Fortunately, the language for which we require this scheme is linear (due to the restriction to affine MACs), and hence we can use (a slight variant of) the highly efficient NIZK scheme from [17].
We stress that this proof blueprint is compatible with the proof of the BKP transformation, even when adapted to many challenges as explained above. In particular, we are able to extend the BKP transformation not only to many challenges, but also (and additionally) to chosen-ciphertext security. The resulting transformation is black-box and works for any given affine MAC that is secure in a many-challenge setting.
1.2 More on Related Work
We are not aware of any (almost) tightly chosen-ciphertext secure IBE scheme in the many-challenge setting. A natural idea is of course to adapt existing (almost) tightly chosen-plaintext secure schemes to chosen-ciphertext security. As we have explained in Sect. 1 above, straightforward generic approaches fail. However, another natural approach is to look at concrete state-of-the-art IBE schemes, and try to use their specific properties. Since we are interested in schemes in prime-order groups for efficiency reasons, the scheme to consider here is that of Gong et al. [22] (cf. also Table 1).
Remark About and Comparison to the Work of Gong et al. Interestingly, Gong et al. also take the BKP scheme as a basis, and extend it to (chosen-plaintext) many-challenge security, even in a setting with many instances of the IBE scheme itself. However, they first interpret and then extend the BKP scheme in the framework of (extended) nested dual system groups [12, 31]. Remarkably, the resulting IBE scheme looks similar to the chosen-plaintext secure, many-challenge scheme that we use as a stepping stone towards many-challenge chosen-ciphertext security. In particular, the efficiency characteristics of those two schemes are comparable.
Still, for the express purpose of achieving chosen-ciphertext security, we found it easier to stick to (an extension of) the original BKP transformation and strategy, for two reasons. First, the modularity of BKP allows us to give an abstract MAC\(\rightarrow \)IBE transformation that achieves chosen-ciphertext security. This allows to isolate the intricate many-challenge security argument for the MAC from the orthogonal argument to achieve chosen-ciphertext security. Since the argument for tight security is directly woven into the notion of (extended) nested dual systems groups, it does not seem clear how to similarly isolate arguments (and proof complexity) for the scheme and strategy of Gong et al.
Second, as hinted above, our strategy to obtain chosen-ciphertext security requires a NIZK proof to show consistency of a ciphertext. With the BKP construction, consistency translates to a statement from a linear language, which allows to employ very efficient NIZK proof systems. For the construction of Gong et al., it is not clear how exactly such a consistency language would look like. In particular, it is not clear at all if highly efficient NIZK proofs for linear languages can be used.Footnote 1
2 Basic Preliminaries
2.1 Notations
We use  to denote the process of sampling an element x from \(\mathcal {S}\) uniformly at random if \(\mathcal {S}\) is a set. For positive integers
to denote the process of sampling an element x from \(\mathcal {S}\) uniformly at random if \(\mathcal {S}\) is a set. For positive integers  and a matrix
and a matrix  , we denote the upper square matrix of \(\mathbf {{A}}\) by
, we denote the upper square matrix of \(\mathbf {{A}}\) by  and the lower \(\eta \) rows of \(\mathbf {{A}}\) by
and the lower \(\eta \) rows of \(\mathbf {{A}}\) by  . Similarly, for a column vector
. Similarly, for a column vector  , we denote the upper k elements by
, we denote the upper k elements by  and the lower \(\eta \) elements of \(\mathbf {{v}}\) by
and the lower \(\eta \) elements of \(\mathbf {{v}}\) by  . For a bit string \(\mathsf {m}\in \{0,1\}^{n}\), \(\mathsf {m}_i\) denotes the ith bit of \(\mathsf {m}\) (\(i\le n\)) and \(\mathsf {m}_{|i}\) denotes the first i bits of \(\mathsf {m}\).
. For a bit string \(\mathsf {m}\in \{0,1\}^{n}\), \(\mathsf {m}_i\) denotes the ith bit of \(\mathsf {m}\) (\(i\le n\)) and \(\mathsf {m}_{|i}\) denotes the first i bits of \(\mathsf {m}\).
All our algorithms are probabilistic polynomial time unless we stated otherwise. If  is an algorithm, then we write
is an algorithm, then we write  to denote the random variable that outputted by
to denote the random variable that outputted by  on input b.
on input b.
Games. We follow [8] to use code-based games for defining and proving security. A game \(\mathsf {G}\) contains procedures \(\textsc {Init}\) and \(\textsc {Finalize}\), and some additional procedures \(\textsc {P}_1,\ldots , \textsc {P}_n\), which are defined in pseudo-code. Initially all variables in a game are undefined (denoted by \(\bot \)), and all sets are empty (denote by \(\emptyset \)). An adversary  is executed in game \(\mathsf {G}\) (denote by
is executed in game \(\mathsf {G}\) (denote by  ) if it first calls \(\textsc {Init}\), obtaining its output. Next, it may make arbitrary queries to \(\textsc {P}_i\) (according to their specification), again obtaining their output. Finally, it makes one single call to \(\textsc {Finalize}(\cdot )\) and stops. We use
) if it first calls \(\textsc {Init}\), obtaining its output. Next, it may make arbitrary queries to \(\textsc {P}_i\) (according to their specification), again obtaining their output. Finally, it makes one single call to \(\textsc {Finalize}(\cdot )\) and stops. We use  to denote that \(\mathsf {G}\) outputs d after interacting with
to denote that \(\mathsf {G}\) outputs d after interacting with  , and d is the output of \(\textsc {Finalize}\).
, and d is the output of \(\textsc {Finalize}\).
2.2 Collision Resistant Hash Functions
Let \(\mathcal {H}\) be a family of hash functions \(H:\{0,1\}^*\rightarrow \{0,1\}^{\lambda }\). We assume that it is efficient to sample a function from \(\mathcal {H}\), which is denoted by  .
.
Definition 1
(Collision resistance). We say a family of hash functions \(\mathcal {H}\) is \((t,\varepsilon )\)-collision-resistant (\(\mathsf {CR}\)) if for all adversaries  that run in time \(t\),
that run in time \(t\),

2.3 Pairing Groups and Matrix Diffie-Hellman Assumptions
Let \(\mathsf {GGen}\) be a probabilistic polynomial time (PPT) algorithm that on input \(1^\lambda \) returns a description  of asymmetric pairing groups where
of asymmetric pairing groups where  ,
,  ,
,  are cyclic groups of order q for a \(\lambda \)-bit prime q, \({P}_1\) and \({P}_2\) are generators of
are cyclic groups of order q for a \(\lambda \)-bit prime q, \({P}_1\) and \({P}_2\) are generators of  and
and  , respectively, and
, respectively, and  is an efficient computable (non-degenerated) bilinear map. Define \({P}_T:=e({P}_1, {P}_2)\), which is a generator in
is an efficient computable (non-degenerated) bilinear map. Define \({P}_T:=e({P}_1, {P}_2)\), which is a generator in  . In this paper, we only consider Type III pairings, where
. In this paper, we only consider Type III pairings, where  and there is no efficient homomorphism between them. All our constructions can be easily instantiated with Type I pairings by setting
and there is no efficient homomorphism between them. All our constructions can be easily instantiated with Type I pairings by setting  and defining the dimension k to be greater than 1.
and defining the dimension k to be greater than 1.
We use implicit representation of group elements as in [16]. For \(s \in \{1,2,T\}\) and  define
define  as the implicit representation of a in
as the implicit representation of a in  . Similarly, for a matrix
. Similarly, for a matrix  we define \([\mathbf {{A}}]_s\) as the implicit representation of \(\mathbf {{A}}\) in
we define \([\mathbf {{A}}]_s\) as the implicit representation of \(\mathbf {{A}}\) in  .
.  denotes the linear span of \(\mathbf {{A}}\), and similarly
denotes the linear span of \(\mathbf {{A}}\), and similarly  . Note that it is efficient to compute \([\mathbf {{AB}}]_s\) given \(([\mathbf {{A}}]_s,\mathbf {{B}})\) or \((\mathbf {{A}},[\mathbf {{B}}]_s)\) with matching dimensions. We define \([\mathbf {{A}}]_1 \circ [\mathbf {{B}}]_2:= e([\mathbf {{A}}]_1,[\mathbf {{B}}]_2) = [\mathbf {{A}} \mathbf {{B}}]_T\), which can be efficiently computed given \([\mathbf {{A}}]_1\) and \([\mathbf {{B}}]_2\).
. Note that it is efficient to compute \([\mathbf {{AB}}]_s\) given \(([\mathbf {{A}}]_s,\mathbf {{B}})\) or \((\mathbf {{A}},[\mathbf {{B}}]_s)\) with matching dimensions. We define \([\mathbf {{A}}]_1 \circ [\mathbf {{B}}]_2:= e([\mathbf {{A}}]_1,[\mathbf {{B}}]_2) = [\mathbf {{A}} \mathbf {{B}}]_T\), which can be efficiently computed given \([\mathbf {{A}}]_1\) and \([\mathbf {{B}}]_2\).
Next we recall the definition of the matrix Diffie-Hellman (\(\mathsf {MDDH}\)) and related assumptions [16].
Definition 2
(Matrix distribution). Let  with \(\ell >k\). We call \(\mathcal {D}_{\ell ,k}\) a matrix distribution if it outputs matrices in
with \(\ell >k\). We call \(\mathcal {D}_{\ell ,k}\) a matrix distribution if it outputs matrices in  of full rank k in polynomial time. Let \(\mathcal {D}_k:=\mathcal {D}_{k+1,k}\).
of full rank k in polynomial time. Let \(\mathcal {D}_k:=\mathcal {D}_{k+1,k}\).
Without loss of generality, we assume the first k rows of  form an invertible matrix. The \(\mathcal {D}_{\ell ,k}\)-Matrix Diffie-Hellman problem is to distinguish the two distributions \(([\mathbf {{A}}], [\mathbf {{A}} \mathbf {{w}}])\) and \(([\mathbf {{A}} ],[\mathbf {{u}}])\) where
form an invertible matrix. The \(\mathcal {D}_{\ell ,k}\)-Matrix Diffie-Hellman problem is to distinguish the two distributions \(([\mathbf {{A}}], [\mathbf {{A}} \mathbf {{w}}])\) and \(([\mathbf {{A}} ],[\mathbf {{u}}])\) where  ,
,  and
and  .
.
Definition 3
(\(\mathcal {D}_{\ell ,k}\)-Matrix Diffie-Hellman assumption). Let \(\mathcal {D}_{\ell ,k}\) be a matrix distribution and \(s \in \{1,2,T\}\). We say that the \(\mathcal {D}_{\ell ,k}\)-Matrix Diffie-Hellman (\(\mathcal {D}_{\ell ,k}\text{- }\mathsf {MDDH}\)) is \((t,\varepsilon )\)-hard relative to \(\mathsf {GGen}\) in group  if for all adversaries
if for all adversaries  with running time \(t\), it holds that
with running time \(t\), it holds that

where the probability is taken over  ,
,  and
and  .
.
We define the \(\mathcal {D}_k\)-Kernel Diffie-Hellman (\(\mathcal {D}_{k}\text{- }\mathsf {KerMDH}\)) assumption [39] which is a natural search variant of the \(\mathcal {D}_{k}\text{- }\mathsf {MDDH}\) assumption.
Definition 4
(\(\mathcal {D}_{k}\)-Kernel Diffie-Hellman assumption). Let \(\mathcal {D}_{k}\) be a matrix distribution and \(s \in \{1,2\}\). We say that the \(\mathcal {D}_{k}\)-kernel Matrix Diffie-Hellman (\(\mathcal {D}_{k}\text{- }\mathsf {KerMDH}\)) is \((t,\varepsilon )\)-hard relative to \(\mathsf {GGen}\) in group  if for all adversaries
if for all adversaries  that runs in time \(t\), it holds that
that runs in time \(t\), it holds that

where the probability is taken over  ,
,  .
.
The following lemma shows that the \(\mathcal {D}_{k}\text{- }\mathsf {KerMDH}\) assumption is a relaxation of the \(\mathcal {D}_k\text{- }\mathsf {MDDH}\) assumption since one can use a non-zero vector in the kernel of \(\mathbf {{A}}\) to test membership in the column space of \(\mathbf {{A}}\).
Lemma 1
(\(\mathcal {D}_k\text{- }\mathsf {MDDH}\Rightarrow \mathcal {D}_{k}\text{- }\mathsf {KerMDH}\) [39]). For any matrix distribution \(\mathcal {D}_k\), if \(\mathcal {D}_{k}\text{- }\mathsf {MDDH}\) is \((t,\varepsilon )\)-hard in  , then \(\mathcal {D}_{k}\text{- }\mathsf {KerMDH}\) is \((t',\varepsilon )\)-hard in
, then \(\mathcal {D}_{k}\text{- }\mathsf {KerMDH}\) is \((t',\varepsilon )\)-hard in  , where \(t'\approx t\).
, where \(t'\approx t\).
The uniform distribution is a particular matrix distribution that deserves special attention, as an adversary breaking the  assumption can also distinguish between real \(\mathsf {MDDH}\) tuples and random tuples for all other possible matrix distributions. For uniform distributions, they stated in [17] that
assumption can also distinguish between real \(\mathsf {MDDH}\) tuples and random tuples for all other possible matrix distributions. For uniform distributions, they stated in [17] that  and
and  assumptions are equivalent.
assumptions are equivalent.
Definition 5
(Uniform distribution). Let  with \(\ell >k\). We call
with \(\ell >k\). We call  a uniform distribution if it outputs uniformly random matrices in
a uniform distribution if it outputs uniformly random matrices in  of rank k in polynomial time.
of rank k in polynomial time.
Lemma 2
(  [16, 17]). For \(\ell >k\), let \(\mathcal {D}_{\ell ,k}\) be a matrix distribution, then if \(\mathcal {D}_{\ell ,k}\text{- }\mathsf {MDDH}\) is \((t,\varepsilon )\)-hard in
[16, 17]). For \(\ell >k\), let \(\mathcal {D}_{\ell ,k}\) be a matrix distribution, then if \(\mathcal {D}_{\ell ,k}\text{- }\mathsf {MDDH}\) is \((t,\varepsilon )\)-hard in  ,
,  is \((t',\varepsilon )\)-hard in
is \((t',\varepsilon )\)-hard in  , where \(t'\approx t\). If
, where \(t'\approx t\). If  is \((t,\varepsilon )\)-hard in
is \((t,\varepsilon )\)-hard in  ,
,  is \((t',\varepsilon )\)-hard in
is \((t',\varepsilon )\)-hard in  , where \(t'\approx t\), vice versa.
, where \(t'\approx t\), vice versa.
For  ,
,  , consider the Q-fold \(\mathcal {D}_{\ell ,k}\text{- }\mathsf {MDDH}\) problem which is distinguishing the distributions \(([\mathbf {{A}}], [\mathbf {{A}} \mathbf {{W}}])\) and \(([\mathbf {{A}}], [\mathbf {{U}}])\). That is, the Q-fold \(\mathcal {D}_{\ell ,k}\text{- }\mathsf {MDDH}\) problem contains Q independent instances of the \(\mathcal {D}_{\ell ,k}\text{- }\mathsf {MDDH}\) problem (with the same \(\mathbf {{A}}\) but different \(\mathbf {{w}}_i\)). The following lemma shows that the two problems are tightly equivalent. The reduction quality is tighter for uniform distribution.
, consider the Q-fold \(\mathcal {D}_{\ell ,k}\text{- }\mathsf {MDDH}\) problem which is distinguishing the distributions \(([\mathbf {{A}}], [\mathbf {{A}} \mathbf {{W}}])\) and \(([\mathbf {{A}}], [\mathbf {{U}}])\). That is, the Q-fold \(\mathcal {D}_{\ell ,k}\text{- }\mathsf {MDDH}\) problem contains Q independent instances of the \(\mathcal {D}_{\ell ,k}\text{- }\mathsf {MDDH}\) problem (with the same \(\mathbf {{A}}\) but different \(\mathbf {{w}}_i\)). The following lemma shows that the two problems are tightly equivalent. The reduction quality is tighter for uniform distribution.
Lemma 3
(Random self-reducibility [16]). For \(\ell >k\) and any matrix distribution \(\mathcal {D}_{\ell ,k}\), \(\mathcal {D}_{\ell ,k}\text{- }\mathsf {MDDH}\) is random self-reducible. In particular, for any \(Q \ge 1\), if \(\mathcal {D}_{\ell ,k}\text{- }\mathsf {MDDH}\) is \((t,\varepsilon )\)-hard relative to \(\mathsf {GGen}\) in group  , then Q-fold \(\mathcal {D}_{\ell ,k}\text{- }\mathsf {MDDH}\) is \((t',\varepsilon ')\)-hard relative to \(\mathsf {GGen}\) in group
, then Q-fold \(\mathcal {D}_{\ell ,k}\text{- }\mathsf {MDDH}\) is \((t',\varepsilon ')\)-hard relative to \(\mathsf {GGen}\) in group  , where \(t\approx t'+Q\cdot \mathsf {poly}(\lambda ),~\varepsilon '\le (\ell -k)\varepsilon +\frac{1}{q-1}\), and for
, where \(t\approx t'+Q\cdot \mathsf {poly}(\lambda ),~\varepsilon '\le (\ell -k)\varepsilon +\frac{1}{q-1}\), and for  , \(\varepsilon '\le \varepsilon +\frac{1}{q-1}\).
, \(\varepsilon '\le \varepsilon +\frac{1}{q-1}\).
3 Affine MACs in the Multi-Challenge Setting
3.1 Definition
We recall the definition of affine MACs from [8] and extend its security requirements of pseudorandomness to the multi-challenge setting.
Definition 6
(Affine MACs). Let \(\mathsf {par}\) be system parameters which contain a pairing group description  of prime order q, and let n be a positive integer, \(\mathsf {MAC}=(\mathsf {Gen}_\mathsf {MAC},\mathsf {Tag},\mathsf {Ver}_\mathsf {MAC})\) is an affine MAC over \(\mathbb {Z}_q^n\) if the following conditions hold:
of prime order q, and let n be a positive integer, \(\mathsf {MAC}=(\mathsf {Gen}_\mathsf {MAC},\mathsf {Tag},\mathsf {Ver}_\mathsf {MAC})\) is an affine MAC over \(\mathbb {Z}_q^n\) if the following conditions hold:
-
1.
 , where \(\mathsf {sk}_{\mathsf {MAC}}=(\mathbf {{B}},\mathbf {{X}}_0,...,\mathbf {{X}}_\ell ,\mathbf {{x}}'_0,...,\mathbf {{x}}'_{\ell '})\in \mathbb {Z}_q^{n\times n'}\times (\mathbb {Z}_q^{\eta \times n})^{\ell +1}\times (\mathbb {Z}_q^{\eta })^{\ell '+1}\), \( n', \ell , \ell '\) and \(\eta \) are positive integers and the rank of \(\mathbf {{B}}\) is at least 1.
, where \(\mathsf {sk}_{\mathsf {MAC}}=(\mathbf {{B}},\mathbf {{X}}_0,...,\mathbf {{X}}_\ell ,\mathbf {{x}}'_0,...,\mathbf {{x}}'_{\ell '})\in \mathbb {Z}_q^{n\times n'}\times (\mathbb {Z}_q^{\eta \times n})^{\ell +1}\times (\mathbb {Z}_q^{\eta })^{\ell '+1}\), \( n', \ell , \ell '\) and \(\eta \) are positive integers and the rank of \(\mathbf {{B}}\) is at least 1. -
2.
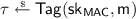 , where
, where  is computed as
is computed as  (2)
(2) (3)
(3)for some public defining functions \(f_i:\mathcal {M}\rightarrow \mathbb {Z}_q\) and \(f'_i:\mathcal {M}\rightarrow \mathbb {Z}_q\). Note that only \(\mathbf {{u}}\) is the message dependent part.
-
3.
\(\mathsf {Ver}_\mathsf {MAC}(\mathsf {sk}_{\mathsf {MAC}},\mathsf {m},\tau =([\mathbf {{t}}]_2,[\mathbf {{u}}]_2))\) output 1 iff (3) holds, 0 otherwise.
Definition 7
An affine \(\mathsf {MAC}\) over  is \(({Q}_{\mathsf {e}},{Q}_{\mathsf {c}},t,\varepsilon )\text{- }\mathsf {mPR}\text{- }\mathsf {CMA}\) (pseudorandom against chosen-message and multi-challenge attacks) if for all
is \(({Q}_{\mathsf {e}},{Q}_{\mathsf {c}},t,\varepsilon )\text{- }\mathsf {mPR}\text{- }\mathsf {CMA}\) (pseudorandom against chosen-message and multi-challenge attacks) if for all  that runs in time \(t\), makes at most \({Q}_{\mathsf {e}}\) queries to the evaluation oracle, \(\textsc {Eval}\), and at most \({Q}_{\mathsf {c}}\) queries to the challenge oracle, \(\textsc {Chal}\), the following holds
that runs in time \(t\), makes at most \({Q}_{\mathsf {e}}\) queries to the evaluation oracle, \(\textsc {Eval}\), and at most \({Q}_{\mathsf {c}}\) queries to the challenge oracle, \(\textsc {Chal}\), the following holds

where experiments \(\mathsf {mPR}\text{- }\mathsf {CMA}_{0}\) and \(\mathsf {mPR}\text{- }\mathsf {CMA}_{1}\) are defined in Fig. 1.
Our notion is a generalization of the \(\mathsf {PR}\text{- }\mathsf {CMA}\) security in [8]. In [8] an adversary  can only query the challenge oracle \(\textsc {Chal}\) at most once, while here
can only query the challenge oracle \(\textsc {Chal}\) at most once, while here  can ask multiple times.
can ask multiple times.
3.2 Instantiation
We extend the tightly secure affine MAC \(\mathsf {MAC}_{\mathsf {NR}}[\mathcal {D}_{k}]\) from [8] to the multi-challenge setting. Instead of choosing random vectors  as the MAC secret keys in the original, here we choose random matrices
as the MAC secret keys in the original, here we choose random matrices  such that in the security proof we can randomize all the tags and at the same time answer multiple challenge queries in a tight way.
such that in the security proof we can randomize all the tags and at the same time answer multiple challenge queries in a tight way.
Let  be an asymmetric pairing group and \(\mathsf {par}:=\mathcal {G}\). Our affine MAC \(\mathsf {MAC}_{\mathsf {NR}}^{\mathsf {mc}}:=(\mathsf {Gen}_\mathsf {MAC}, \mathsf {Tag}, \mathsf {Ver}_\mathsf {MAC})\) for message space \(\{0,1\}^L\) is defined as follows.
be an asymmetric pairing group and \(\mathsf {par}:=\mathcal {G}\). Our affine MAC \(\mathsf {MAC}_{\mathsf {NR}}^{\mathsf {mc}}:=(\mathsf {Gen}_\mathsf {MAC}, \mathsf {Tag}, \mathsf {Ver}_\mathsf {MAC})\) for message space \(\{0,1\}^L\) is defined as follows.

Our scheme can be present by using any \(\mathcal {D}_{2k,k}\) distribution and some of them have compact representation and give more efficient scheme. For simplicity of presentation, we present our scheme based on the \(\mathcal {U}_{2k,k}\) distribution.
Games \(\mathsf {G}_0\), \(\mathsf {G}_{1,i}\) (\(0 \le i \le L\)), \(\mathsf {G}_2\), \(\mathsf {G}_3\) for the proof of Theorem 1.  is a random function. Boxed codes are only executed in the games marked in the same box style at the top right of every procedure. Non-boxed codes are always run.
is a random function. Boxed codes are only executed in the games marked in the same box style at the top right of every procedure. Non-boxed codes are always run.
Theorem 1
If the  problem is \((t_1,\varepsilon _1)\)-hard in
problem is \((t_1,\varepsilon _1)\)-hard in  and \((t_2,\varepsilon _2)\)-hard in
and \((t_2,\varepsilon _2)\)-hard in  , the
, the  -\(\mathsf {MDDH}\) problem is \((t_3,\varepsilon _3)\)-hard in
-\(\mathsf {MDDH}\) problem is \((t_3,\varepsilon _3)\)-hard in  , then \(\mathsf {MAC}_{\mathsf {NR}}^{\mathsf {mc}}\) is
, then \(\mathsf {MAC}_{\mathsf {NR}}^{\mathsf {mc}}\) is  -\(\mathsf {mPR}\text{- }\mathsf {CMA}\)-secure with
-\(\mathsf {mPR}\text{- }\mathsf {CMA}\)-secure with  , and \(\varepsilon \le 4L\varepsilon _1 + 3 L\varepsilon _2+3\varepsilon _3 +2^{-\varOmega (\lambda )}\), where \(\mathsf {poly}(\lambda )\) is independent of
, and \(\varepsilon \le 4L\varepsilon _1 + 3 L\varepsilon _2+3\varepsilon _3 +2^{-\varOmega (\lambda )}\), where \(\mathsf {poly}(\lambda )\) is independent of  .
.
Proof
We prove the theorem via a sequence of games as shown in Fig. 2.
Lemma 4
(\(\mathsf {G}_{0}\) to \(\mathsf {G}_{1,0}\)).  .
.
Proof
\(\mathsf {G}_{0}\) is the original game and it is the same as \(\mathsf {mPR}\text{- }\mathsf {CMA}_{0}\). In \(\mathsf {G}_{1,0}\), we define \(\mathsf {RF}_{0}(\epsilon )\) as a fix random vector  and then have Lemma 4. \(\square \)
and then have Lemma 4. \(\square \)
Lemma 5
(\(\mathsf {G}_{1,i}\) to \(\mathsf {G}_{1,i+1}\)). If the \(\mathcal {U}_{2k,k}\)-\(\mathsf {MDDH}\) problem is \((t_1,\varepsilon _1)\)-hard in  and \((t_2,\varepsilon _2)\)-hard in
and \((t_2,\varepsilon _2)\)-hard in  , then
, then  and
and  where \(\mathsf {poly}(\lambda )\) is independent of
where \(\mathsf {poly}(\lambda )\) is independent of  .
.
Proof
(of Lemma 5). To bound the difference between  and \(\mathsf {G}_{1,i+1}\), we introduce a series of intermediate games \(\mathsf {H}_{i,1}\) to \(\mathsf {H}_{i,5}\) as in Fig. 3. An overview of the transitions is given in Fig. 4.
and \(\mathsf {G}_{1,i+1}\), we introduce a series of intermediate games \(\mathsf {H}_{i,1}\) to \(\mathsf {H}_{i,5}\) as in Fig. 3. An overview of the transitions is given in Fig. 4.
Games \(\mathsf {G}_{1,i}\), \(\mathsf {G}_{1,i+1}\), \(\mathsf {H}_{i,1}\),..., \(\mathsf {H}_{i,5}\) (\(0 \le i \le L\)) for the proof of Lemma 5.  ,
,  are three independent random functions.
are three independent random functions.
Overview of the transitions in the proof of Lemma 5. We highlight the respective changes between the games in
 .
.  , and
, and  are three independent random functions.
are three independent random functions.
Lemma 6
(\(\mathsf {G}_{1,i}\) to \(\mathsf {H}_{i,1}\)). If the \(\mathcal {U}_{2k,k}\text{- }\mathsf {MDDH}\) problem is \((t_1,\varepsilon _1)\)-hard in  , then
, then  where \(\mathsf {poly}(\lambda )\) is independent of
where \(\mathsf {poly}(\lambda )\) is independent of  .
.
Proof
Let  . We define an intermediate game \(\mathsf {H}^{'}_{i,1}\) which is the same as \(\mathsf {G}_{1,i}\) except for \(\textsc {Chal}\): precisely, if \(\mathsf {m}^{*}_{i+1}=0\) then we pick \(\mathbf {{h}}\) uniformly random from \(\mathsf {Span}(\mathbf {{A}}_0)\); otherwise,
. We define an intermediate game \(\mathsf {H}^{'}_{i,1}\) which is the same as \(\mathsf {G}_{1,i}\) except for \(\textsc {Chal}\): precisely, if \(\mathsf {m}^{*}_{i+1}=0\) then we pick \(\mathbf {{h}}\) uniformly random from \(\mathsf {Span}(\mathbf {{A}}_0)\); otherwise,  . Oracles \(\textsc {Init}, \textsc {Eval}\) and \(\textsc {Finalize}\) are simulated as in \(\mathsf {G}_{1,i}\).
. Oracles \(\textsc {Init}, \textsc {Eval}\) and \(\textsc {Finalize}\) are simulated as in \(\mathsf {G}_{1,i}\).
The difference between \(\mathsf {G}_{1,i}\) and \(\mathsf {H}'_{i,1}\) is bounded by a straightforward reduction to break the \({Q}_{\mathsf {c}}\)-fold \(\mathcal {U}_{2k,k}\)-\(\mathsf {MDDH}\) problem in  with \([\mathbf {{A}}_0]_1\) as the challenge matrix. Thus, by Lemma 3 we have
with \([\mathbf {{A}}_0]_1\) as the challenge matrix. Thus, by Lemma 3 we have

Similarly, we can bound \(\mathsf {H}'_{i,1}\) and \(\mathsf {H}_{i,1}\) with the \(\mathcal {U}_{2k,k}\)-\(\mathsf {MDDH}\) assumption in  , namely,
, namely,

Here we have  , where \(\mathsf {poly}(\lambda )\) is independent of
, where \(\mathsf {poly}(\lambda )\) is independent of  . \(\square \)
. \(\square \)
After switching \([\mathbf {{h}}]_1\) in \(\textsc {Chal}\) to the right span, the following reductions can have \(\mathbf {{A}}_0 \) and \(\mathbf {{A}}_1\) over  . Since the rank of \(\mathbf {{A}}_0\) and that of \(\mathbf {{A}}_1\) are both k, we can efficiently compute the kernel matrix
. Since the rank of \(\mathbf {{A}}_0\) and that of \(\mathbf {{A}}_1\) are both k, we can efficiently compute the kernel matrix  (resp. \(\mathbf {{A}}_1^{\bot }\)) of \(\mathbf {{A}}_0\) (resp. \(\mathbf {{A}}_1\)). We note that \(\mathbf {{A}}_0^\top \mathbf {{A}}_0^{\bot }= \mathbf {{0}} = \mathbf {{A}}_1^\top \mathbf {{A}}_1^{\bot }\) and
(resp. \(\mathbf {{A}}_1^{\bot }\)) of \(\mathbf {{A}}_0\) (resp. \(\mathbf {{A}}_1\)). We note that \(\mathbf {{A}}_0^\top \mathbf {{A}}_0^{\bot }= \mathbf {{0}} = \mathbf {{A}}_1^\top \mathbf {{A}}_1^{\bot }\) and  is a full-rank matrix with overwhelming probability \(1-2^{-\varOmega (\lambda )}\), since \(\mathbf {{A}}_0\) and \(\mathbf {{A}}_1\) are two random matrices.
is a full-rank matrix with overwhelming probability \(1-2^{-\varOmega (\lambda )}\), since \(\mathbf {{A}}_0\) and \(\mathbf {{A}}_1\) are two random matrices.
Let \(\mathsf {ZF}_i \) and \(\mathsf {OF}_i\) be two independent random functions mapping from \(\{0,1\}^i\) to  .
.
Lemma 7
(
\(\mathsf {H}_{i,1}\)
to
\(\mathsf {H}_{i,2}\)
).

Proof
The difference between these two games is statistically bounded. In \(\mathsf {H}_{i,2}\), we just rewrite \(\mathsf {RF}_{i}(\mathsf {m}_{|i})\) as
Since \((\mathbf {{A}}_0^{\bot }\mid \mathbf {{A}}_1^{\bot })\) is a full-rank matrix with overwhelming probability \(1-\frac{k}{q}\) and \(\mathsf {ZF}_{i}\),  are two independent random functions,
are two independent random functions,  in (4) is a random function as well. Thus, \(\mathsf {H}_{i,1}\) and \(\mathsf {H}_{i,2}\) are distributed the same except with probability \(2^{-\varOmega (\lambda )}\). \(\square \)
in (4) is a random function as well. Thus, \(\mathsf {H}_{i,1}\) and \(\mathsf {H}_{i,2}\) are distributed the same except with probability \(2^{-\varOmega (\lambda )}\). \(\square \)
The following step is a main difference to \(\mathsf {MAC}_{\mathsf {NR}}[{\mathcal {D}_k}]\) in the original BKP framework [8]. Here our reduction can randomize \(\textsc {Eval}\) queries with the \(\mathsf {MDDH}\) assumption and at the same time it can answer multiple \(\textsc {Chal}\) queries, while the original \(\mathsf {MAC}_{\mathsf {NR}}[{\mathcal {D}_k}]\) can not. Precisely, to be able to go from \(\mathsf {RF}_{i}\) to \(\mathsf {RF}_{i+1}\), the security reduction of \(\mathsf {MAC}_{\mathsf {NR}}[{\mathcal {D}_k}]\) (cf. Lemma 3.6 in [8]) guesses  which stands for the \((i+1)\)-th bit of \(\mathsf {m}^{*}\) and implicitly embeds \(\mathbf {{T}}_{\mathbf {{D}}} := \underline{\mathbf {{D}}} \overline{\mathbf {{D}}}^{-1}\) in the secret key \(\mathbf {{x}}_{i+1,1-b}\). Note that the reduction does not know \(\mathbf {{x}}_{i+1,1-b}\), but, since the adversary
which stands for the \((i+1)\)-th bit of \(\mathsf {m}^{*}\) and implicitly embeds \(\mathbf {{T}}_{\mathbf {{D}}} := \underline{\mathbf {{D}}} \overline{\mathbf {{D}}}^{-1}\) in the secret key \(\mathbf {{x}}_{i+1,1-b}\). Note that the reduction does not know \(\mathbf {{x}}_{i+1,1-b}\), but, since the adversary  only has at most one query to \(\textsc {Chal}\) and b is hidden from
only has at most one query to \(\textsc {Chal}\) and b is hidden from  , the reduction can hope \(\mathsf {m}^{*}_{i+1}\ne 1-b\) (with probability 1 / 2) and it can simulate the experiment. However, this proof strategy does not work in the multi-challenge setting, since
, the reduction can hope \(\mathsf {m}^{*}_{i+1}\ne 1-b\) (with probability 1 / 2) and it can simulate the experiment. However, this proof strategy does not work in the multi-challenge setting, since  can ask two challenge queries with one query which has b in the \((i+1)\)-th position and \(1-b\) in the other.
can ask two challenge queries with one query which has b in the \((i+1)\)-th position and \(1-b\) in the other.
By increasing the dimension of \(\mathbf {{X}}_{j,\beta }\), our strategy is first embedding \(\mathbf {{A}}_0^{\bot }\mathbf {{T}}_{\mathbf {{D}}}\) in \(\mathbf {{X}}_{i+1,0}\) such that we can add entropy to \(\mathbf {{x}}'_\mathsf {m}\) in the span of \(\mathbf {{A}}_0^{\bot }\) and at the same time upon \(\textsc {Chal}\) queries with 0 in the \((i+1)\)-th position \(\mathbf {{T}}_{\mathbf {{D}}}\) will be canceled out, and then add entropy to \(\mathbf {{x}}'_\mathsf {m}\) in the span of \(\mathbf {{A}}_1^{\bot }\) in the similar way.
Lemma 8
(\(\mathsf {H}_{i,2}\) to \(\mathsf {H}_{i,3}\)). If the \(\mathcal {U}_{2k,k}\)-\(\mathsf {MDDH}\) problem is \((t_2,\varepsilon _2)\)-hard in  , then
, then  , where \(\mathsf {poly}(\lambda )\) is independent of
, where \(\mathsf {poly}(\lambda )\) is independent of  .
.
Proof
We bound the difference between \(\mathsf {H}_{i,2}\) and \(\mathsf {H}_{i,3}\) by the \({Q}_{\mathsf {e}}\)-fold  assumption in
assumption in  . Formally, on receiving a \({Q}_{\mathsf {e}}\)-fold
. Formally, on receiving a \({Q}_{\mathsf {e}}\)-fold  challenge
challenge  , where \({Q}_{\mathsf {e}}\) denotes the number of evaluation queries, we construct a reduction
, where \({Q}_{\mathsf {e}}\) denotes the number of evaluation queries, we construct a reduction  as in Fig. 5. Let \(\mathsf {ZF}_i,\mathsf {ZF}'_i\) be two independent random functions, we define \(\mathsf {ZF}_{i+1}\) as
as in Fig. 5. Let \(\mathsf {ZF}_i,\mathsf {ZF}'_i\) be two independent random functions, we define \(\mathsf {ZF}_{i+1}\) as
Note that \(\mathsf {ZF}_{i+1}\) is a random function, given \(\mathsf {ZF}_{i}\) and \(\mathsf {ZF}'_i\) are two independent random functions. If an adversary  queries messages \(\mathsf {m}\) with \(\mathsf {m}_{i+1}=1\) to \(\textsc {Eval}\) and \(\textsc {Chal}\), then
queries messages \(\mathsf {m}\) with \(\mathsf {m}_{i+1}=1\) to \(\textsc {Eval}\) and \(\textsc {Chal}\), then  ’s view in \(\mathsf {H}_{i,2}\) is the same as that in \(\mathsf {H}_{i,3}\). Thus, we only focus on messages with \(\mathsf {m}_{i+1}=0\).
’s view in \(\mathsf {H}_{i,2}\) is the same as that in \(\mathsf {H}_{i,3}\). Thus, we only focus on messages with \(\mathsf {m}_{i+1}=0\).
Description of  for proving Lemma 8.
for proving Lemma 8.
For queries with \(\textsc {Chal}\), if \(\mathsf {m}^{*}_{i+1}=0\),  does not have \(\mathbf {{X}}_{i+1,0} = \hat{\mathbf {{X}}} + \mathbf {{A}}_0^{\bot }\underline{\mathbf {{D}}} \overline{\mathbf {{D}}}^{-1}\), since
does not have \(\mathbf {{X}}_{i+1,0} = \hat{\mathbf {{X}}} + \mathbf {{A}}_0^{\bot }\underline{\mathbf {{D}}} \overline{\mathbf {{D}}}^{-1}\), since  does not know \(\underline{\mathbf {{D}}} \overline{\mathbf {{D}}}^{-1}\) either over
does not know \(\underline{\mathbf {{D}}} \overline{\mathbf {{D}}}^{-1}\) either over  or
or  , but, since \(\mathbf {{h}} \in \mathsf {Span}(\mathbf {{A}}_0)\) for such \(\mathsf {m}^{*}\), \((\mathbf {{A}}_0^{\bot }\underline{\mathbf {{D}}} \overline{\mathbf {{D}}}^{-1})^\top \mathbf {{h}} = \mathbf {{0}}\) and thus
, but, since \(\mathbf {{h}} \in \mathsf {Span}(\mathbf {{A}}_0)\) for such \(\mathsf {m}^{*}\), \((\mathbf {{A}}_0^{\bot }\underline{\mathbf {{D}}} \overline{\mathbf {{D}}}^{-1})^\top \mathbf {{h}} = \mathbf {{0}}\) and thus  computes
computes
For queries with \(\textsc {Eval}\), if \(\mathsf {m}_{i+1}=0\), we write \(\mathbf {{f}}_c := \begin{pmatrix} \overline{\mathbf {{D}}} \mathbf {{w}}_c \\ \underline{\mathbf {{D}}} \mathbf {{w}}_c + \mathbf {{r}}_c \end{pmatrix}\) for some  , where
, where  is \(\mathbf {{0}}\) if \([\mathbf {{F}}]_2\) is from the real \(\mathcal {U}_{2k,k}\)-\(\mathsf {MDDH}\) distribution, or \(\mathbf {{r}}_c\) is random otherwise. Then, we have
is \(\mathbf {{0}}\) if \([\mathbf {{F}}]_2\) is from the real \(\mathcal {U}_{2k,k}\)-\(\mathsf {MDDH}\) distribution, or \(\mathbf {{r}}_c\) is random otherwise. Then, we have
Now it is clear that if \(\mathbf {{r}}_c = \mathbf {{0}}\) then \(\mathbf {{u}}_{\mathsf {m}}\) is distributed as in \(\mathsf {H}_{i,2}\); if \(\mathbf {{r}}_c\) is random, then we define \(\mathsf {ZF}'_{i}(\mathsf {m}_{|i}) := \mathbf {{r}}_c \) and \(\mathbf {{u}}_\mathsf {m}\) is distributed as in \(\mathsf {H}_{i,3}\). \(\square \)
The proof of Lemma 9 is very similar to that of Lemma 8 except that it handles cases with \(\mathsf {m}_{i+1}=1\). More precisely, we define
where \(\mathsf {OF}_{i}, \mathsf {OF}'_{i}\) are two independent random functions mapping from \(\{0,1\}^i\) to  . By the similar arguments of Lemma 8, we have the following lemma.
. By the similar arguments of Lemma 8, we have the following lemma.
Lemma 9
(\(\mathsf {H}_{i,3}\) to \(\mathsf {H}_{i,4}\)). If the \(\mathcal {U}_{2k,k}\)-\(\mathsf {MDDH}\) problem is \((t_2,\varepsilon _2)\)-hard in  , then
, then 
Lemmata 10 and 11 are the reverse of Lemmata 6 and 7, and we omit the detailed proofs.
Lemma 10
(
\(\mathsf {H}_{i,4}\)
to
\(\mathsf {H}_{i,5}\)
).

Lemma 11
(\(\mathsf {H}_{i,5}\) to \(\mathsf {G}_{1,i+1}\)). If the \(\mathcal {U}_{2k,k}\)-\(\mathsf {MDDH}\) problem is \((t_1,\varepsilon _1)\)-hard in  , then
, then  where \(\mathsf {poly}(\lambda )\) is independent of
where \(\mathsf {poly}(\lambda )\) is independent of  .
.
Lemma 12
(\(\mathsf {G}_{1,L}\) to \(\mathsf {G}_2\)). If the \(\mathcal {U}_{2k}\)-\(\mathsf {MDDH}\) problem is \((t_3,\varepsilon _3)\)-hard in  , then
, then

where \(\mathsf {poly}(\lambda )\) is independent of  .
.
Proof
Firstly we bound the difference between \(\mathsf {G}_{1,L}\) and \(\mathsf {G}_{2'}\) by the \({Q}_{\mathsf {c}}\)-fold  assumption in
assumption in  , where \(\mathsf {G}'_2\) is the same as \(\mathsf {G}_{1,L}\) except that on a challenge query, we pick a random
, where \(\mathsf {G}'_2\) is the same as \(\mathsf {G}_{1,L}\) except that on a challenge query, we pick a random  for each query in \(\mathsf {G}'_2\).
for each query in \(\mathsf {G}'_2\).
Formally, on receiving a \({Q}_{\mathsf {c}}\)-fold  challenge
challenge  , where \({Q}_{\mathsf {c}}\) denotes the number of challenge queries, we construct a reduction
, where \({Q}_{\mathsf {c}}\) denotes the number of challenge queries, we construct a reduction  as in Fig. 6.
as in Fig. 6.
For \(\textsc {Eval}\) queries, since \(\mathbf {{u}}_{\mathsf {m}}\) is information-theoretically hidden by \(\mathsf {RF}(\mathsf {m})\), we can just pick \(\mathbf {{u}}_{\mathsf {m}}\) uniformly random. For \(\textsc {Chal}\) queries, we write \(\mathbf {{f}}_c := \begin{pmatrix} \overline{\mathbf {{D}}} \mathbf {{w}}_c \\ \underline{\mathbf {{D}}} \mathbf {{w}}_c + {r}_c \end{pmatrix}\) for some  , where
, where  is 0 if \([\mathbf {{F}}]_2\) is from the real
is 0 if \([\mathbf {{F}}]_2\) is from the real  -\(\mathsf {MDDH}\) distribution, and \({r}_c\) is random otherwise. Then, we have
-\(\mathsf {MDDH}\) distribution, and \({r}_c\) is random otherwise. Then, we have
If \({r}_c = {0}\) then \(h_1\) is distributed as in \(\mathsf {G}_{1,L}\); if \({r}_c\) is random then \(h_1\) is distributed as in \(\mathsf {G}'_{2}\).
Next we bound the difference between \(\mathsf {G}'_{2}\) and \(\mathsf {G}''_{2}\) by the \({Q}_{\mathsf {c}}\)-fold  assumption in
assumption in  , where \(\mathsf {G}''_2\) is the same as \(\mathsf {G}^{'}_{2}\) except that when answering \(\textsc {Chal}\) with \(\mathsf {m}^{*}_1=0\), one picks a random
, where \(\mathsf {G}''_2\) is the same as \(\mathsf {G}^{'}_{2}\) except that when answering \(\textsc {Chal}\) with \(\mathsf {m}^{*}_1=0\), one picks a random  for each query. And the difference between \(\mathsf {G}'_{2}\) and \(\mathsf {G}''_{2}\) can be bounded by the \({Q}_{\mathsf {c}}\)-fold
for each query. And the difference between \(\mathsf {G}'_{2}\) and \(\mathsf {G}''_{2}\) can be bounded by the \({Q}_{\mathsf {c}}\)-fold  assumption in
assumption in  . Formally, on receiving a \({Q}_{\mathsf {c}}\)-fold
. Formally, on receiving a \({Q}_{\mathsf {c}}\)-fold  challenge
challenge  , where \({Q}_{\mathsf {c}}\) denotes the number of challenge queries, we construct a reduction
, where \({Q}_{\mathsf {c}}\) denotes the number of challenge queries, we construct a reduction  as in Fig. 7.
as in Fig. 7.
For \(\textsc {Eval}(\mathsf {m})\) queries, since \(\mathbf {{u}}_{\mathsf {m}}\) is information-theoretically hidden by \(\mathsf {RF}(\mathsf {m})\), here we just pick \(\mathbf {{u}}_{\mathsf {m}}\) uniformly random.
For \(\textsc {Chal}(\mathsf {m}^{*})\) queries, if \(\mathsf {m}^{*}_1=1\), \(\mathsf {G}''_2\) and \(\mathsf {G}'_2\) are the same, if \(\mathsf {m}^{*}_1=0\), we write \(\mathbf {{f}}_c := \begin{pmatrix} \overline{\mathbf {{D}}} \mathbf {{w}}_c \\ \underline{\mathbf {{D}}} \mathbf {{w}}_c + \mathbf {{r}}_c \end{pmatrix}\) for some  , where
, where  is \(\mathbf {{0}}\) if \([\mathbf {{F}}]_2\) is from the real \(\mathcal {U}_{3k,2k}\)-\(\mathsf {MDDH}\) distribution, and \(\mathbf {{r}}_c\) is random otherwise. Then, we have
is \(\mathbf {{0}}\) if \([\mathbf {{F}}]_2\) is from the real \(\mathcal {U}_{3k,2k}\)-\(\mathsf {MDDH}\) distribution, and \(\mathbf {{r}}_c\) is random otherwise. Then, we have
If \(\mathbf {{r}}_c = \mathbf {{0}}\) then \(\mathbf {{h}}_0\) is distributed as in \(\mathsf {G}'_{2}\); if \(\mathbf {{r}}_c\) is random then \(\mathbf {{h}}_0\) is distributed as in \(\mathsf {G}''_{2}\). The difference between \(\mathsf {G}''_2\) and \(\mathsf {G}_2\) can be bounded by the \({Q}_{\mathsf {c}}\)-fold  -\(\mathsf {MDDH}\) assumption in a similar way. \(\square \)
-\(\mathsf {MDDH}\) assumption in a similar way. \(\square \)
\(\square \)
We perform all the previous changes of Fig. 2 in a reverse order without changing the simulation of \(\textsc {Chal}\). Then we have the following lemma.
Lemma 13
(\(\mathsf {G}_{2}\) to \(\mathsf {G}_3\)). If the \(\mathcal {U}_{3k,k}\)-\(\mathsf {MDDH}\) problem is \((t_2,\varepsilon _2)\)-hard in  , then
, then  and
and  , where \(\mathsf {poly}(\lambda )\) is independent of
, where \(\mathsf {poly}(\lambda )\) is independent of  .
.
By observing \(\mathsf {G}_3\) is the same as \(\mathsf {mPR}\text{- }\mathsf {CMA}_{1}\), we sum up Lemmata 4 to 13 and conclude Theorem 1. \(\square \)
4 Quasi-adaptive Zero-Knowledge Arguments for Linear Subspaces
4.1 Definition
The notion of quasi-adaptive non-interactive zero-knowledge arguments (\(\mathsf {QANIZK}\)) is proposed by Jutla and Roy [33], where the common reference string \(\mathsf {CRS}\) depends on the specific language for which proofs are generated. In the following we define a tag-based variant of \(\mathsf {QANIZK}\) [17, 34]. For simplicity, we only consider arguments for linear subspaces.
Let \(\mathsf {par}\) be the public parameters for \(\mathsf {QANIZK}\) and \(\mathcal {D}_{\mathsf {par}}\) be a probability distribution over a collection of relations \(R=\{R_{[\mathbf {{M}}]_1}\}\) parametrized by a matrix  (\(n> t\)) with associated language
(\(n> t\)) with associated language  . We consider witness sampleable distributions [33] where there is an efficiently sampleable distribution \(\mathcal {D}'_{\mathsf {par}}\) outputs
. We consider witness sampleable distributions [33] where there is an efficiently sampleable distribution \(\mathcal {D}'_{\mathsf {par}}\) outputs  such that \([\mathbf {{M}}']_1\) distributes the same as \([\mathbf {{M}}]_1\). We note that the matrix distribution in Definition 2 is sampleable.
such that \([\mathbf {{M}}']_1\) distributes the same as \([\mathbf {{M}}]_1\). We note that the matrix distribution in Definition 2 is sampleable.
Definition 8
(Tag-based \(\mathsf {QANIZK}\)). A tag-based quasi-adaptive non-interactive zero-knowledge argument (\(\mathsf {QANIZK}\)) for a language distribution \(\mathcal {D}_{\mathsf {par}}\) consists of four PPT algorithms \(\varPi =(\mathsf {Gen}_{\mathsf {NIZK}},\mathsf {Prove},\mathsf {Ver}_{\mathsf {NIZK}},\mathsf {Sim})\).
-
The key generation algorithm \(\mathsf {Gen}_{\mathsf {NIZK}}(\mathsf {par},[\mathbf {{M}}]_1)\) returns a common reference string \(\mathsf {crs}\) and the trapdoor \(\mathsf {td}\), where \(\mathsf {crs}\) defines a tag space \(\mathcal {T}\).
-
The proving algorithm \(\mathsf {Prove}(\mathsf {crs},\mathsf {tag},[\mathbf {{c}}_0]_1,\mathbf {{r}})\) returns a proof \(\pi \).
-
The deterministic verification algorithm \(\mathsf {Ver}_{\mathsf {NIZK}}(\mathsf {crs},\mathsf {tag},[\mathbf {{c}}_0]_1,\pi )\) returns 1 or 0, where 1 indicates that \(\pi \) is a valid proof for \([\mathbf {{c}}_0]_1\in \mathcal {L}_{[\mathbf {{M}}]_1}\).
-
The simulation algorithm \(\mathsf {Sim}(\mathsf {crs},\mathsf {td},\mathsf {tag},[\mathbf {{c}}_0]_1)\) returns a proof \(\pi \) for \([\mathbf {{c}}_0]_1 \in \mathcal {L}_{[\mathbf {{M}}]_1}\).
(Perfect Completeness.) For all \(\lambda \), all \([\mathbf {{M}}]_1\), all \(([\mathbf {{c}}_0]_1,\mathbf {{r}})\) with \([\mathbf {{c}}_0]_1=[\mathbf {{M}}\mathbf {{r}}]_1\), all \((\mathsf {crs},\mathsf {td}) \in \mathsf {Gen}_{\mathsf {NIZK}}(\mathsf {par},[\mathbf {{M}}]_1)\), and all \(\pi \in \mathsf {Prove}(\mathsf {crs},\mathsf {tag},[\mathbf {{c}}_0]_1,\mathbf {{r}})\), we have \(\mathsf {Ver}_{\mathsf {NIZK}}(\mathsf {crs},\mathsf {tag},[\mathbf {{c}}_0]_1,\pi )=1\).
We require \(\varPi \) to have the following security. Here we require a stronger version of unbounded simulation soundness than the usual one in [17, 34], where an adversary is allowed to submit a forgery with a reused tag.
Definition 9 (Perfect Zero-Knowledge)
A tag-based \(\mathsf {QANIZK}\) \(\varPi \) is perfectly zero-knowledge if for all \(\lambda \), all \([\mathbf {{M}}]_1\), all \(([\mathbf {{c}}_0]_1,\mathbf {{r}})\) with \([\mathbf {{c}}_0]_1=[\mathbf {{M}}\mathbf {{r}}]_1\), and all \((\mathsf {crs},\mathsf {td})\in \mathsf {Gen}_{\mathsf {NIZK}}(\mathsf {par},[\mathbf {{M}}]_1)\), the following two distributions are identical:
Definition 10
(Unbounded Simulation Soundness). A tag-based \(\mathsf {QANIZK}\) \(\varPi \) is  if for any adversary
if for any adversary  that runs in time \(t\), it holds that
that runs in time \(t\), it holds that  , where Game \(\mathsf {USS}\) is defined in Fig. 8.
, where Game \(\mathsf {USS}\) is defined in Fig. 8.
4.2 Construction: QANIZK with Unbounded Simulation Soundness
We (slightly) modify the QANIZK scheme in [17] to achieve our stronger unbounded simulation soundness (as in Definition 10). Let  be the system parameter, where
be the system parameter, where  is chosen uniformly from a collision-resistant hash function family \(\mathcal {H}\). Our QANIZK scheme \(\varPi \) is defined as in Figure 9.
is chosen uniformly from a collision-resistant hash function family \(\mathcal {H}\). Our QANIZK scheme \(\varPi \) is defined as in Figure 9.
Theorem 2
The QANIZK system \(\varPi _\mathsf {uss}\) defined in Fig. 9 has perfect completeness and perfect zero-knowledge. Suppose in addition that the distribution of matrix \(\mathbf {{M}}\) is witness sampleable, the \(\mathcal {D}_{k}\text{- }\mathsf {MDDH}\) is \((t_1,\varepsilon _1)\)-hard in  , the \(\mathcal {D}_{k}\text{- }\mathsf {KerMDH}\) is \((t_2,\varepsilon _2)\)-hard in
, the \(\mathcal {D}_{k}\text{- }\mathsf {KerMDH}\) is \((t_2,\varepsilon _2)\)-hard in  , \(\mathcal {H}\) is a \((t_3,\varepsilon _3)\)-collision resistant hash function family, then \(\varPi _\mathsf {uss}\) is \((t,\varepsilon )\text{- }\mathsf {USS}\), where \(t_1\approx t_2\approx t_3\approx t+{Q}_{\mathsf {s}}\mathsf {poly}(\lambda )\), and \(\varepsilon \le \varepsilon _2+4\lambda \varepsilon _1+\varepsilon _3+2^{-\varOmega (\lambda )}\), \(\mathsf {poly}(\lambda )\) is a polynomial independent of \(t\).
, \(\mathcal {H}\) is a \((t_3,\varepsilon _3)\)-collision resistant hash function family, then \(\varPi _\mathsf {uss}\) is \((t,\varepsilon )\text{- }\mathsf {USS}\), where \(t_1\approx t_2\approx t_3\approx t+{Q}_{\mathsf {s}}\mathsf {poly}(\lambda )\), and \(\varepsilon \le \varepsilon _2+4\lambda \varepsilon _1+\varepsilon _3+2^{-\varOmega (\lambda )}\), \(\mathsf {poly}(\lambda )\) is a polynomial independent of \(t\).
The proof is similar to that of [17] and we give the formal proof in the full version.
5 Identity-Based Key Encapsulation Mechanism
We give our generic construction of an identity-based key encapsulation mechanism (IBKEM) from an affine MAC. Here we only focus on IBKEMs, since, even in the multi-instance, multi-challenge setting, a constrained CCA (resp. CPA) secure IBKEM can be transformed to a CCA (resp. CPA) secure identity-based encryption (IBE) in an efficient and tightly secure way by using an authenticated symmetric encryption scheme. One can prove this by adapting the known techniques from [20, 30] in a straightforward way.
5.1 Definition
Let \(\mathsf {par}\) be a set of system parameters.
Definition 11
(Identity-based key encapsulation mechanism). An identity-based key encapsulation mechanism (IBKEM) has four algorithms \(\mathsf {IBKEM}:=(\mathsf {Setup},{\mathsf {Ext}},{\mathsf {Enc}},{\mathsf {Dec}})\) with the following properties:
-
The key generation algorithm \(\mathsf {Setup}(\mathsf {par})\) returns the (master) public/secret key \((\mathsf {pk},\mathsf {sk})\). We assume that \(\mathsf {pk}\) implicitly defines an identity space \(\mathcal {ID}\), a symmetric key space \(\mathcal {K}\), and a ciphertext space \(\mathcal {C}\).
-
The user secret-key generation algorithm \({\mathsf {Ext}}(\mathsf {sk},\mathsf {id})\) returns a user secret key \(\mathsf {usk}[\mathsf {id}]\) for an identity \(\mathsf {id} \in \mathcal {ID}\).
-
The encapsulation algorithm \({\mathsf {Enc}}(\mathsf {pk},\mathsf {id})\) returns a symmetric key \(\mathsf {K}\in \mathcal {K}\) together with a ciphertext \(\mathsf {C}\in \mathcal {C}\) with respect to identity \(\mathsf {id}\).
-
The deterministic decapsulation algorithm \({\mathsf {Dec}}(\mathsf {usk}[\mathsf {id}],\mathsf {id},\mathsf {C})\) returns the decapsulated key \(\mathsf {K}\in \mathcal {K}\) or the rejection symbol \(\bot \).
(Perfect correctness). We require that for all pairs  , all identities
, all identities  , all
, all  and all
and all  , \(\Pr [{\mathsf {Dec}}(\mathsf {usk}[\mathsf {id}],\mathsf {id},\mathsf {C})=\mathsf {K}]=1.\)
, \(\Pr [{\mathsf {Dec}}(\mathsf {usk}[\mathsf {id}],\mathsf {id},\mathsf {C})=\mathsf {K}]=1.\)
We define indistinguishability against constrained chosen-ciphertext and chosen-identity attacks for IBKEM in the multi-challenge setting.
Definition 12
(\(\mathsf {mID}\text{- }\mathsf {CCCA}\) security). An identity-based key encapsulation scheme \(\mathsf {IBKEM}\) is \((Q_{\mathsf {ext}},Q_{\mathsf {enc}},Q_{\mathsf {dec}},t,\varepsilon )\text{- }\mathsf {mID}\text{- }\mathsf {CCCA}\)-secure if for all  with negligible
with negligible  that runs in time \(t\), makes at most \(Q_{\mathsf {ext}}\) user secret-key queries, \(Q_{\mathsf {enc}}\) encryption queries and \(Q_{\mathsf {dec}}\) decryption queries,
that runs in time \(t\), makes at most \(Q_{\mathsf {ext}}\) user secret-key queries, \(Q_{\mathsf {enc}}\) encryption queries and \(Q_{\mathsf {dec}}\) decryption queries,

where the security game is defined as in Fig. 10, here \(\mathsf {pred}_i: \mathcal {K}\rightarrow \{ 0,1 \}\) denotes the predicate sent in the ith decryption query, the uncertainty of knowledge about keys corresponding to decryption queries is defined as

If an adversary is not allowed to query \(\textsc {Dec}\), then we get the security notion of indistinguishability against chosen-plaintext and chosen-identity attacks.
Definition 13
(\(\mathsf {mID}\text{- }\mathsf {CPA}\) security). An identity-based key encapsulation scheme \(\mathsf {IBKEM}\) is \((Q_{\mathsf {ext}},Q_{\mathsf {enc}},t,\varepsilon )\text{- }\mathsf {mID}\text{- }\mathsf {CPA}\)-secure if \(\mathsf {IBKEM}\) is \((Q_{\mathsf {ext}},Q_{\mathsf {enc}},0,t,\varepsilon )\text{- }\mathsf {mID}\text{- }\mathsf {CCCA}\)-secure.
Remark 1
(\(\textsc {Ext}\) queries with the same identity). For simplicity, we assume that an adversary can query \(\textsc {Ext}\) with the same identity at most once. This is without loss of generality when assuming that the scheme is made deterministic, e.g., by generating the randomness in \(\textsc {Ext}\) with a (tightly secure) pseudorandom function such as the Naor-Reingold PRF [40]. Thus the anonymity we achieve here is usually called weak anonymity [22].
Remark 2
(On  ). When we prove the IND-CCA security of the hybrid IBE scheme by combining an IND-CCCA secure ID-KEM together with an unconditionally one-time secure authenticated encryption scheme \(\mathsf {AE}\), the term
). When we prove the IND-CCA security of the hybrid IBE scheme by combining an IND-CCCA secure ID-KEM together with an unconditionally one-time secure authenticated encryption scheme \(\mathsf {AE}\), the term  is related to the one-time integrity of \(\mathsf {AE}\) and can be made exponentially small (since it does not necessarily rely on any computational assumption). Hence, in line with previous works (e.g., [17]), we still call our reduction (almost) tight.
is related to the one-time integrity of \(\mathsf {AE}\) and can be made exponentially small (since it does not necessarily rely on any computational assumption). Hence, in line with previous works (e.g., [17]), we still call our reduction (almost) tight.
5.2 Two Transformations
We construct two generic transformations of IBKEM from affine MACs, \(\mathsf {IBKEM}_1\) and \(\mathsf {IBKEM}_2\). Let  , \(\mathsf {MAC}:=(\mathsf {Gen}_\mathsf {MAC},\mathsf {Tag},\mathsf {Ver}_\mathsf {MAC})\) be an affine MAC and \(\varPi :=(\mathsf {Gen}_{\mathsf {NIZK}},\mathsf {Prove},\mathsf {Ver}_{\mathsf {NIZK}},\mathsf {Sim})\) be a QANIZK system for linear language
, \(\mathsf {MAC}:=(\mathsf {Gen}_\mathsf {MAC},\mathsf {Tag},\mathsf {Ver}_\mathsf {MAC})\) be an affine MAC and \(\varPi :=(\mathsf {Gen}_{\mathsf {NIZK}},\mathsf {Prove},\mathsf {Ver}_{\mathsf {NIZK}},\mathsf {Sim})\) be a QANIZK system for linear language  , where
, where  . Our IBKEMs \(\mathsf {IBKEM}_1\) and \(\mathsf {IBKEM}_2\) are defined in Fig. 11.
. Our IBKEMs \(\mathsf {IBKEM}_1\) and \(\mathsf {IBKEM}_2\) are defined in Fig. 11.
It is worth mentioning that if we instantiate our schemes with the \(\mathsf {SXDH}\) assumption then we have: 4 elements in user secret keys, 4 elements in ciphertexts, and \((2\lambda +4)\) elements in master public keys for \(\mathsf {IBKEM}_1\) (which is denoted by \((|\mathsf {usk}|, |\mathsf {C}|,|\mathsf {pk}|) =(4,4,2\lambda +4)\)); and \((|\mathsf {usk}|, |\mathsf {C}|,|\mathsf {pk}|) = (4,7,8\lambda + 12)\) for \(\mathsf {IBKEM}_2\). We give concrete instantiations in the full version based on the \(\mathsf {MDDH}\) and \(\mathsf {SXDH}\) assumptions, respectively.
\(\mathsf {IBKEM}_1\) is \(\mathsf {mID}\text{- }\mathsf {CPA}\)-secure and it follows the same idea as \(\mathsf {IBE}[\mathsf {MAC},\mathcal {D}_{k}]\) in [8]. Since our underlying MAC is secure in the multi-challenge setting, \(\mathsf {IBKEM}_1\) is ID-CPA-secure in the multi-challenge setting, and it can be also viewed as an alternative abstraction of [22] in the BKP framework.
The difficulty for \(\mathsf {IBKEM}_1\) to achieve \(\mathsf {mID}\text{- }\mathsf {CCCA}\) security is that decryption answers may leak information about \(\mathsf {usk}[\mathsf {id}]\) for challenge \(\mathsf {id}\). We observe that if ciphertexts satisfy that \((\mathbf {{c}}_0=\mathbf {{M}}\mathbf {{r}}) \wedge (\mathbf {{c}}_1=(\sum _{i=0}^{\ell } f_i(\mathsf {id}) \mathbf {{Z}}_i )\cdot \mathbf {{r}})\) for some \(\mathbf {{r}}\) (we call such ciphertexts as “well-formed”), then the decrypted \(\mathsf {K}\) reveals no more information about \(\mathsf {usk}[\mathsf {id}]\) than \(\mathsf {pk}\). Since “\(\mathbf {{c}}_0\in \mathsf {Span}(\mathbf {{M}})\)” is a linear statement, we can introduce the efficient unbounded simulation-sound QANIZK from Section 4 to reject \(\textsc {Dec}\) queries with \([\mathbf {{c}}_0]_1 \notin \mathsf {Span}([\mathbf {{M}}]_1)\). Furthermore, due to the randomness contained in \(\mathsf {usk}[\mathsf {id}]\), if \(\mathbf {{c}}_0\in \mathsf {Span}(\mathbf {{M}})\) but \(\mathbf {{c}}_1\) is not “well-formed”, the decrypted \(\mathsf {K}\) will be randomly distributed and thus it will be rejected by the decryption oracle. Note that \([\mathbf {{c}}_1]_1\) works as the tag for \(\mathsf {QANIZK}\) argument. We refer the proof of Theorem 4 for technical details.
Theorem 3
(\(\mathsf {mID}\text{- }\mathsf {CPA}\) Security of \(\mathsf {IBKEM}_1\)). If the  is \((t_1,\varepsilon _1)\)-hard in
is \((t_1,\varepsilon _1)\)-hard in  , and \(\mathsf {MAC}\) is a \(({Q}_{\mathsf {e}},{Q}_{\mathsf {c}},t_2,\varepsilon _2)\text{- }\mathsf {mPR}\text{- }\mathsf {CMA}\)-secure affine MAC, then \(\mathsf {IBKEM}_1\) is \((Q_{\mathsf {ext}},Q_{\mathsf {enc}},t,\varepsilon )\text{- }\mathsf {mID}\text{- }\mathsf {CPA}\)-secure, where \(Q_{\mathsf {ext}}\le {Q}_{\mathsf {e}},Q_{\mathsf {enc}}\le {Q}_{\mathsf {c}}\), \(t_1\approx t_2\approx t+(Q_{\mathsf {ext}}+Q_{\mathsf {enc}})\mathsf {poly}(\lambda )\) and \(\varepsilon \le 2(\varepsilon _1+\varepsilon _2+2^{-\varOmega (\lambda )})\).
, and \(\mathsf {MAC}\) is a \(({Q}_{\mathsf {e}},{Q}_{\mathsf {c}},t_2,\varepsilon _2)\text{- }\mathsf {mPR}\text{- }\mathsf {CMA}\)-secure affine MAC, then \(\mathsf {IBKEM}_1\) is \((Q_{\mathsf {ext}},Q_{\mathsf {enc}},t,\varepsilon )\text{- }\mathsf {mID}\text{- }\mathsf {CPA}\)-secure, where \(Q_{\mathsf {ext}}\le {Q}_{\mathsf {e}},Q_{\mathsf {enc}}\le {Q}_{\mathsf {c}}\), \(t_1\approx t_2\approx t+(Q_{\mathsf {ext}}+Q_{\mathsf {enc}})\mathsf {poly}(\lambda )\) and \(\varepsilon \le 2(\varepsilon _1+\varepsilon _2+2^{-\varOmega (\lambda )})\).
The proof of Theorem 3 is an extension of Theorem 4.3 in [8] in the multi-challenge setting. We leave the proof in the full version.
Theorem 4
(\(\mathsf {mID}\text{- }\mathsf {CCCA}\) Security of \(\mathsf {IBKEM}_2\)). If the  is \((t_1,\varepsilon _1)\)-hard in
is \((t_1,\varepsilon _1)\)-hard in  , \(\mathsf {MAC}\) is a \(({Q}_{\mathsf {e}},{Q}_{\mathsf {c}},t_2,\varepsilon _2)\text{- }\mathsf {mPR}\text{- }\mathsf {CMA}\)-secure affine MAC, \(\varPi \) is a \(({Q}_{\mathsf {s}},t_3,\varepsilon _3)\)-\(\mathsf {USS}\) QANIZK, then \(\mathsf {IBKEM}_2\) is \((Q_{\mathsf {ext}},Q_{\mathsf {enc}},Q_{\mathsf {dec}},t,\varepsilon )\text{- }\mathsf {mID}\text{- }\mathsf {CCCA}\)-secure, where \(Q_{\mathsf {ext}}\le {Q}_{\mathsf {e}}\), \(Q_{\mathsf {enc}}\le {Q}_{\mathsf {c}}\approx {Q}_{\mathsf {s}}\), \(t_3\approx t_1\approx t_2\approx t+(Q_{\mathsf {dec}}+Q_{\mathsf {enc}}+Q_{\mathsf {ext}})\mathsf {poly}(\lambda )\) and
, \(\mathsf {MAC}\) is a \(({Q}_{\mathsf {e}},{Q}_{\mathsf {c}},t_2,\varepsilon _2)\text{- }\mathsf {mPR}\text{- }\mathsf {CMA}\)-secure affine MAC, \(\varPi \) is a \(({Q}_{\mathsf {s}},t_3,\varepsilon _3)\)-\(\mathsf {USS}\) QANIZK, then \(\mathsf {IBKEM}_2\) is \((Q_{\mathsf {ext}},Q_{\mathsf {enc}},Q_{\mathsf {dec}},t,\varepsilon )\text{- }\mathsf {mID}\text{- }\mathsf {CCCA}\)-secure, where \(Q_{\mathsf {ext}}\le {Q}_{\mathsf {e}}\), \(Q_{\mathsf {enc}}\le {Q}_{\mathsf {c}}\approx {Q}_{\mathsf {s}}\), \(t_3\approx t_1\approx t_2\approx t+(Q_{\mathsf {dec}}+Q_{\mathsf {enc}}+Q_{\mathsf {ext}})\mathsf {poly}(\lambda )\) and  .
.
It is easy to verify the correctness of \(\mathsf {IBKEM}_1\) and \(\mathsf {IBKEM}_2\).
Proof
(of Theorem 4). We define a series of games in Fig. 12 to prove the \(\mathsf {mID}\text{- }\mathsf {CCCA}\) security of \(\mathsf {IBKEM}_2\). A brief overview of game changes is described as in Fig. 13. For a simple presentation of Fig. 12, we define \(\mathbf {{X}}_{\mathsf {id}}:=\sum _{i=0}^{\ell }f_i(\mathsf {id})\mathbf {{X}}_i\), \(\mathbf {{Y}}_{\mathsf {id}}:=\sum _{i=0}^{\ell }f_i(\mathsf {id})\mathbf {{Y}}_i\), \(\mathbf {{Z}}_{\mathsf {id}}:=\sum _{i=0}^{\ell }f_i(\mathsf {id})\mathbf {{Z}}_i\), \(\mathbf {{x}}'_{\mathsf {id}}:=\sum _{i=0}^{\ell '}f'_i(\mathsf {id})\mathbf {{x}}'_i\), \(\mathbf {{y}}'_{\mathsf {id}}:=\sum _{i=0}^{\ell '}f'_i(\mathsf {id})\mathbf {{y}}'_i\), \(\mathbf {{z}}'_{\mathsf {id}}:=\sum _{i=0}^{\ell '}f'_i(\mathsf {id})\mathbf {{z}}'_i\) for an \(\mathsf {id} \in \{0,1\}^L\).
Games \(\mathsf {G}_0 \text{- }\mathsf {G}_6\) for the proof of Theorem 4.
Overview of game changes for proof of Theorem 4
Lemma 14
(
\(\mathsf {G}_0\)
to
\(\mathsf {G}_1\)
).

Proof
\(\mathsf {G}_0\) is the real attack game. In \(\mathsf {G}_1\), we change the simulation of \(\mathbf {{c}}_1\) and K in \(\textsc {Enc}(\mathsf {id}^*)\) by substituting \(\mathbf {{Z}}_i\) and \(\mathbf {{z}}'_i\) with their respective definitions:
and \(K=(\mathbf {{y}}'^\top _{\mathsf {id}^*}\mid \mathbf {{x}}'^\top _{\mathsf {id}^*}) \mathbf {{M}} \mathbf {{r}}=({\mathbf {{y}}'_{\mathsf {id}^*}}^\top \mid {\mathbf {{x}}'_{\mathsf {id}^*}}^{\top }) \mathbf {{c}}_0\). This change is only conceptual. Moreover, we simulate the \(\mathsf {QANIZK}\) proof \(\pi \) in \(\textsc {Enc}(\mathsf {id}^*)\) by using \(\varPi \)’s zero-knowledge simulator. By the perfect zero-knowledge property of \(\varPi \), \(\mathsf {G}_1\) is identical to \(\mathsf {G}_0\). \(\square \)
Lemma 15
(\(\mathsf {G}_1\) to \(\mathsf {G}_2\)). If the \(\mathcal {U}_{k+\eta ,k}\text{- }\mathsf {MDDH}\) problem is \((t_1,\varepsilon _1)\)-hard in  , then
, then  and
and  , where \(\mathsf {poly}\) is a polynomial independent of
, where \(\mathsf {poly}\) is a polynomial independent of  .
.
Lemma 15 can be proved by a straightforward reduction to the \(Q_{\mathsf {enc}}\)-fold  problem in
problem in  and we omit it here.
and we omit it here.
Lemma 16
(\(\mathsf {G}_2\) to \(\mathsf {G}_3\)). If the tag-based \(\mathsf {QANIZK}\) \(\varPi \) is \(({Q}_{\mathsf {s}},t_3,\varepsilon _3)\text{- }\mathsf {USS}\), then  , where \(\mathsf {poly}\) is a polynomial independent of
, where \(\mathsf {poly}\) is a polynomial independent of  .
.
Proof
The difference between \(\mathsf {G}_2\) and \(\mathsf {G}_3\) happens when an adversary queries the decryption oracle \(\textsc {Dec}\) with \((\mathsf {id},\mathsf {C}=([\mathbf {{c}}_0]_1,[\mathbf {{c}}_1]_1,\pi ),\mathsf {pred})\) where \(\mathsf {id}\notin \mathcal {Q}_{\mathsf {usk}}\wedge \mathsf {pred}({\mathsf {Dec}}(\mathsf {usk}[\mathsf {id}],\mathsf {id},\mathsf {C}))=1 \wedge \mathbf {{c}}_0\notin \mathsf {Span}(\mathbf {{M}}) \wedge \mathsf {Ver}_{\mathsf {NIZK}}(\mathsf {crs},[\mathbf {{c}}_1]_1,[\mathbf {{c}}_0]_1,\pi )=1\). That is bounded by the unbounded simulation soundness (\(\mathsf {USS}\)) of \(\varPi \). Formally, we construct an algorithm  in Fig. 14 to break the \(\mathsf {USS}\) of \(\varPi \) and we highlight the important steps with gray.
in Fig. 14 to break the \(\mathsf {USS}\) of \(\varPi \) and we highlight the important steps with gray.
We analyze the success probability of  . For a \(\textsc {Dec}(\mathsf {id},\mathsf {C},\mathsf {pred}_i)\) query, we have the following two cases:
. For a \(\textsc {Dec}(\mathsf {id},\mathsf {C},\mathsf {pred}_i)\) query, we have the following two cases:
-
\(([\mathbf {{c}}_1]_1,[\mathbf {{c}}_0]_1,\pi )=([\mathbf {{c}}_1^*]_1,[\mathbf {{c}}^*_0]_1,\pi ^*)\) for some \((\mathsf {id}^*,\mathsf {C}^*)\in \mathcal {C}_{\mathsf {enc}}\) with \(\mathsf {id} \ne \mathsf {id}^*\). In this case,
 cannot break the \(\mathsf {USS}\) property, but the adversary
cannot break the \(\mathsf {USS}\) property, but the adversary  can ask such a query with \(\mathsf {pred}_i({\mathsf {Dec}}(\mathsf {usk}[\mathsf {id}],\mathsf {id},\mathsf {C}))=1\) with probability
can ask such a query with \(\mathsf {pred}_i({\mathsf {Dec}}(\mathsf {usk}[\mathsf {id}],\mathsf {id},\mathsf {C}))=1\) with probability  . More precisely, we have $$\begin{aligned} \mathsf {K}&=[\mathbf {{c}}_0^{\top }]_1 \circ [ \mathbf {{w}}]_2-[\mathbf {{c}}_1^{\top }]_1 \circ [\mathbf {{t}}]_2\\&=[\mathbf {{c}}_0^{\top }]_1 \circ [ \mathbf {{w}}]_2-[\mathbf {{c}}_0 ^{\top }(\mathbf {{Y}}_{\mathsf {id}^*}\mid \mathbf {{X}}_{\mathsf {id}^*})]_1 \circ [\mathbf {{t}}]_2\\&=[\mathbf {{c}}_0^{\top }]_1 \circ [ (\mathbf {{Y}}_{\mathsf {id}}\mid \mathbf {{X}}_{\mathsf {id}})\mathbf {{t}}]_2-[\mathbf {{c}}_0 ^{\top }(\mathbf {{Y}}_{\mathsf {id}^*}\mid \mathbf {{X}}_{\mathsf {id}^*})]_1 \circ [\mathbf {{t}}]_2\\&=[\mathbf {{c}}_0^{\top }]_1 \circ [ (\mathbf {{Y}}_{\varDelta }\mid \mathbf {{X}}_{\varDelta })\mathbf {{t}}]_2, \end{aligned}$$
. More precisely, we have $$\begin{aligned} \mathsf {K}&=[\mathbf {{c}}_0^{\top }]_1 \circ [ \mathbf {{w}}]_2-[\mathbf {{c}}_1^{\top }]_1 \circ [\mathbf {{t}}]_2\\&=[\mathbf {{c}}_0^{\top }]_1 \circ [ \mathbf {{w}}]_2-[\mathbf {{c}}_0 ^{\top }(\mathbf {{Y}}_{\mathsf {id}^*}\mid \mathbf {{X}}_{\mathsf {id}^*})]_1 \circ [\mathbf {{t}}]_2\\&=[\mathbf {{c}}_0^{\top }]_1 \circ [ (\mathbf {{Y}}_{\mathsf {id}}\mid \mathbf {{X}}_{\mathsf {id}})\mathbf {{t}}]_2-[\mathbf {{c}}_0 ^{\top }(\mathbf {{Y}}_{\mathsf {id}^*}\mid \mathbf {{X}}_{\mathsf {id}^*})]_1 \circ [\mathbf {{t}}]_2\\&=[\mathbf {{c}}_0^{\top }]_1 \circ [ (\mathbf {{Y}}_{\varDelta }\mid \mathbf {{X}}_{\varDelta })\mathbf {{t}}]_2, \end{aligned}$$where \(\mathbf {{Y}}_\varDelta :=\mathbf {{Y}}_{\mathsf {id}} - \mathbf {{Y}}_{\mathsf {id}^*}\) and \(\mathbf {{X}}_\varDelta :=\mathbf {{X}}_{\mathsf {id}} - \mathbf {{X}}_{\mathsf {id}^*}\). By \(\mathsf {id}\notin \mathcal {Q}_{\mathsf {usk}}\), the corresponding \(\mathbf {{t}}\) is randomly distributed in the adversary’s view. Clearly, \((\mathbf {{Y}}_\varDelta \mid \mathbf {{X}}_\varDelta )\ne \mathbf {{0}}\), since \(\mathsf {id} \ne \mathsf {id}^*\). Thus, \(\mathsf {K}\) is randomly distributed and
 can output a \(\mathsf {pred}_i\) such that \(\mathsf {pred}_i(\mathsf {K})=1\) with probability
can output a \(\mathsf {pred}_i\) such that \(\mathsf {pred}_i(\mathsf {K})=1\) with probability  .
. -
\(([\mathbf {{c}}_1]_1,[\mathbf {{c}}_0]_1,\pi )\ne ([\mathbf {{c}}^*_1]_1,[\mathbf {{c}}^*_0]_1,\pi ^*)\) for all \((\mathsf {id}^*,\mathsf {C}^*)\in \mathcal {C}_{\mathsf {enc}}\). In this case, \(([\mathbf {{c}}_1]_1,[\mathbf {{c}}_0]_1,\pi )\) is a valid proof to break the \(\mathsf {USS}\) of \(\varPi \).
To sum up, the success probability of  is at least
is at least  . \(\square \)
. \(\square \)
Lemma 17
(\(\mathsf {G}_3\) to \(\mathsf {G}_4\)).  .
.
Proof
An adversary  can distinguish \(\mathsf {G}_{4}\) from \(\mathsf {G}_{3}\) if
can distinguish \(\mathsf {G}_{4}\) from \(\mathsf {G}_{3}\) if  asks the decryption oracle \(\textsc {Dec}\) with \((\mathsf {id},\mathsf {C}=([\mathbf {{c}}_0]_1,[\mathbf {{c}}_1]_1,\pi ),\mathsf {pred})\) where \(\mathbf {{c}}_1\ne \mathbf {{Z}}_{\mathsf {id}}\overline{{\mathbf {{M}}}}^{-1} \cdot \overline{{\mathbf {{c}}_0}}\) but \(\mathsf {pred}({\mathsf {Dec}}(\mathsf {usk}[\mathsf {id}],\mathsf {id},\mathsf {C}))=1\).
asks the decryption oracle \(\textsc {Dec}\) with \((\mathsf {id},\mathsf {C}=([\mathbf {{c}}_0]_1,[\mathbf {{c}}_1]_1,\pi ),\mathsf {pred})\) where \(\mathbf {{c}}_1\ne \mathbf {{Z}}_{\mathsf {id}}\overline{{\mathbf {{M}}}}^{-1} \cdot \overline{{\mathbf {{c}}_0}}\) but \(\mathsf {pred}({\mathsf {Dec}}(\mathsf {usk}[\mathsf {id}],\mathsf {id},\mathsf {C}))=1\).
We show that, before an identity \(\mathsf {id}\) is queried to \(\textsc {Ext}\), for any \((\mathbf {{c}}_0,\mathbf {{c}}_1)\), the value  is uniformly random from the adversary’s view, where \(([\mathbf {{t}}_{\mathsf {id}}]_2,[\mathbf {{u}}_{\mathsf {id}}]_2,[\mathbf {{v}}_{\mathsf {id}}]_2) \in \textsc {Ext}(\mathsf {id})\):
is uniformly random from the adversary’s view, where \(([\mathbf {{t}}_{\mathsf {id}}]_2,[\mathbf {{u}}_{\mathsf {id}}]_2,[\mathbf {{v}}_{\mathsf {id}}]_2) \in \textsc {Ext}(\mathsf {id})\):

In \(\mathsf {G}_3\) and \(\mathsf {G}_4\), a \(\textsc {Dec}\) query with \(\mathbf {{c}}_0\notin \mathsf {Span}(\mathbf {{M}})\) and \(\mathsf {id}\notin \mathcal {Q}_{\mathsf {usk}}\) will be rejected, and thus we have \(\varDelta _1=\mathbf {{0}}\). As \(\mathsf {id}\) has never been queried to \(\textsc {Ext}\), \(\mathbf {{t}}_\mathsf {id}\) is uniformly random to the adversary. Thus, if \(\mathbf {{c}}_1\ne \mathbf {{Z}}_{\mathsf {id}}\overline{{\mathbf {{M}}}}^{-1} \overline{{\mathbf {{c}}_0}}\) (namely, \(\varDelta _2\ne \mathbf {{0}}\)) then K is random and a query of this form will be rejected except with probability  . By the union bound, the difference between \(\mathsf {G}_3\) and \(\mathsf {G}_4\) is bounded by
. By the union bound, the difference between \(\mathsf {G}_3\) and \(\mathsf {G}_4\) is bounded by  . \(\square \)
. \(\square \)
Lemma 18
(\(\mathsf {G}_4\) to \(\mathsf {G}_5\)).  .
.
Proof
The change from \(\mathsf {G}_4\) to \(\mathsf {G}_5\) is only conceptual. By \(\mathbf {{Z}}_i=(\mathbf {{Y}}^\top _i\mid \mathbf {{X}}_i^{\top })\mathbf {{M}}\), we have \(\mathbf {{Y}}^\top _i=(\mathbf {{Z}}_i-\mathbf {{X}}_i^{\top } \cdot \underline{\mathbf {{M}}})\cdot (\overline{\mathbf {{M}}})^{-1}\), and similarly we have \(\mathbf {{y}}'^\top _i=(\mathbf {{z}}'_i-\mathbf {{x}}'^{\top }_i\cdot \underline{\mathbf {{M}}})\cdot \overline{\mathbf {{M}}}^{-1}\). For \(\textsc {Ext}(\mathsf {id})\), by substituting \(\mathbf {{Y}}^\top _i\) and \(\mathbf {{y}}'^\top _i\), we obtain
Note that we can compute \([\mathbf {{v}}]_2\) in \(\mathsf {G}_5\), since \(\mathbf {{A}}\), \(\mathbf {{z}}'_i\) and \(\mathbf {{Z}}_i\) are known explicitly over  and \([\mathbf {{t}}]_2\) and \([\mathbf {{u}}]_2\) are known.
and \([\mathbf {{t}}]_2\) and \([\mathbf {{u}}]_2\) are known.
\(\mathbf {{c}}_0\) from \(\textsc {Enc}(\mathsf {id}^*)\) is uniformly random in \(\mathsf {G}_4\) and \(\mathsf {G}_5\). By \(\mathbf {{h}}=\underline{\mathbf {{c}}_0}-\underline{\mathbf {{M}}}\cdot \overline{\mathbf {{M}}}^{-1}\overline{\mathbf {{c}}_0}\), we have
and \(\mathbf {{c}}_1\) is distributed as in \(\mathsf {G}_4\). The distribution of \(\mathsf {K}\) can be proved by a similar argument. \(\square \)
Lemma 19
(\(\mathsf {G}_5\) to \(\mathsf {G}_6\)). If \(\mathsf {MAC}\) is \(({Q}_{\mathsf {e}},{Q}_{\mathsf {c}},t_2,\varepsilon _2)\text{- }\mathsf {mPR}\text{- }\mathsf {CMA}\)-secure, then  with
with  , where \(\mathsf {poly}\) is a polynomial independent of
, where \(\mathsf {poly}\) is a polynomial independent of  .
.
Proof
In \(\mathsf {G}_6\), we answer the \(\textsc {Enc}(\mathsf {id})\) query by choosing random \(\mathsf {K}\) and \(([\mathbf {{c}}_0]_1,[\mathbf {{c}}_1]_1)\). We construct an adversary  in Fig. 15 to bound the differences between \(\mathsf {G}_5\) and \(\mathsf {G}_6\) with the \(\mathsf {mPR}\text{- }\mathsf {CMA}\) security of \(\mathsf {MAC}\). The decryption oracle \(\textsc {Dec}\) is simulated as in \(\mathsf {G}_{5}\) and \(\mathsf {G}_6\). Now if
in Fig. 15 to bound the differences between \(\mathsf {G}_5\) and \(\mathsf {G}_6\) with the \(\mathsf {mPR}\text{- }\mathsf {CMA}\) security of \(\mathsf {MAC}\). The decryption oracle \(\textsc {Dec}\) is simulated as in \(\mathsf {G}_{5}\) and \(\mathsf {G}_6\). Now if  is in \(\mathsf {mPR}\text{- }\mathsf {CMA}_{1}\) then the simulated distribution is identical to \(\mathsf {G}_{6}\); otherwise, it is identical to \(\mathsf {G}_{5}\). \(\square \)
is in \(\mathsf {mPR}\text{- }\mathsf {CMA}_{1}\) then the simulated distribution is identical to \(\mathsf {G}_{6}\); otherwise, it is identical to \(\mathsf {G}_{5}\). \(\square \)
We observe that \(\mathsf {G}_6\) is computationally indistinguishable from \(\mathsf {mID}\text{- }\mathsf {CCCA}_{\mathsf {rand}}\) by a reverse arguments of Lemmata 14 to 19 without changing the distribution of \(\mathsf {K}\) in \(\textsc {Enc}\). More precisely, we can argue this by switching the ciphertexts from random to real and removing all the additional rejection rules in \(\textsc {Dec}\). Thus, we conclude Theorem 4. \(\square \)
Remark 3
(Anonymity). In \(\mathsf {G}_{6}\) all the challenge ciphertexts are independent of the challenge identity \(\mathsf {id}^*\): \([\mathbf {{c}}_1]_1\) is uniform and \([\mathbf {{c}}_0]_1\) and \(\pi \) are independent of \(\mathsf {id}^*\). Thus, our scheme is trivially anonymous.
Notes
- 1.
To be clear: we do not claim that the scheme of Gong et al. cannot be upgraded to chosen-ciphertext security. However, it seems that such an upgrade would require a more complex restructuring of their proof strategy.
References
Abe, M., David, B., Kohlweiss, M., Nishimaki, R., Ohkubo, M.: Tagged one-time signatures: tight security and optimal tag size. In: Kurosawa, K., Hanaoka, G. (eds.) PKC 2013. LNCS, vol. 7778, pp. 312–331. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-36362-7_20
Abe, M., Hofheinz, D., Nishimaki, R., Ohkubo, M., Pan, J.: Compact structure-preserving signatures with almost tight security. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017. LNCS, vol. 10402, pp. 548–580. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63715-0_19
Attrapadung, N., Hanaoka, G., Yamada, S.: A framework for identity-based encryption with almost tight security. In: Iwata, T., Cheon, J.H. (eds.) ASIACRYPT 2015. LNCS, vol. 9452, pp. 521–549. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48797-6_22
Auerbach, B., Cash, D., Fersch, M., Kiltz, E.: Memory-tight reductions. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017. LNCS, vol. 10401, pp. 101–132. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63688-7_4
Bader, C., Hofheinz, D., Jager, T., Kiltz, E., Li, Y.: Tightly-secure authenticated key exchange. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015. LNCS, vol. 9014, pp. 629–658. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46494-6_26
Bellare, M., Boldyreva, A., Micali, S.: Public-key encryption in a multi-user setting: security proofs and improvements. In: Preneel, B. (ed.) EUROCRYPT 2000. LNCS, vol. 1807, pp. 259–274. Springer, Heidelberg (2000). https://doi.org/10.1007/3-540-45539-6_18
Bellare, M., Goldwasser, S.: New paradigms for digital signatures and message authentication based on non-interactive zero knowledge proofs. In: Brassard, G. (ed.) CRYPTO 1989. LNCS, vol. 435, pp. 194–211. Springer, New York (1990). https://doi.org/10.1007/0-387-34805-0_19
Blazy, O., Kiltz, E., Pan, J.: (Hierarchical) identity-based encryption from affine message authentication. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014. LNCS, vol. 8616, pp. 408–425. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-44371-2_23
Boneh, D., Canetti, R., Halevi, S., Katz, J.: Chosen-ciphertext security from identity-based encryption. SIAM J. Comput. 36(5), 1301–1328 (2007)
Boneh, D., Mironov, I., Shoup, V.: A secure signature scheme from bilinear maps. In: Joye, M. (ed.) CT-RSA 2003. LNCS, vol. 2612, pp. 98–110. Springer, Heidelberg (2003). https://doi.org/10.1007/3-540-36563-X_7
Chen, J., Gong, J., Weng, J.: Tightly secure IBE under constant-size master public key. In: Fehr, S. (ed.) PKC 2017. LNCS, vol. 10174, pp. 207–231. Springer, Heidelberg (2017). https://doi.org/10.1007/978-3-662-54365-8_9
Chen, J., Wee, H.: Fully, (almost) tightly secure ibe and dual system groups. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013. LNCS, vol. 8043, pp. 435–460. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40084-1_25
Chevallier-Mames, B., Joye, M.: A practical and tightly secure signature scheme without hash function. In: Abe, M. (ed.) CT-RSA 2007. LNCS, vol. 4377, pp. 339–356. Springer, Heidelberg (2006). https://doi.org/10.1007/11967668_22
Cramer, R., Shoup, V.: Universal hash proofs and a paradigm for adaptive chosen ciphertext secure public-key encryption. In: Knudsen, L.R. (ed.) EUROCRYPT 2002. LNCS, vol. 2332, pp. 45–64. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-46035-7_4
Cramer, R., Shoup, V.: Design and analysis of practical public-key encryption schemes secure against adaptive chosen ciphertext attack. SIAM J. Comput. 33(1), 167–226 (2003)
Escala, A., Herold, G., Kiltz, E., Ràfols, C., Villar, J.: An algebraic framework for diffie-hellman assumptions. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013. LNCS, vol. 8043, pp. 129–147. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40084-1_8
Gay, R., Hofheinz, D., Kiltz, E., Wee, H.: Tightly CCA-secure encryption without pairings. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016. LNCS, vol. 9665, pp. 1–27. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49890-3_1
Gay, R., Hofheinz, D., Kohl, L., Pan, J.: More efficient (almost) tightly secure structure-preserving signatures. In: Nielsen, J.B., Rijmen, V. (eds.) EUROCRYPT 2018. LNCS, vol. 10821, pp. 230–258. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-78375-8_8
Gentry, C.: Practical identity-based encryption without random oracles. In: Vaudenay, S. (ed.) EUROCRYPT 2006. LNCS, vol. 4004, pp. 445–464. Springer, Heidelberg (2006). https://doi.org/10.1007/11761679_27
Giacon, F., Kiltz, E., Poettering, B.: Hybrid encryption in a multi-user setting, revisited. In: Abdalla, M., Dahab, R. (eds.) PKC 2018. LNCS, vol. 10769, pp. 159–189. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-76578-5_6
Gong, J., Chen, J., Dong, X., Cao, Z., Tang, S.: Extended nested dual system groups, revisited. In: Cheng, C.-M., Chung, K.-M., Persiano, G., Yang, B.-Y. (eds.) PKC 2016. LNCS, vol. 9614, pp. 133–163. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49384-7_6
Gong, J., Dong, X., Chen, J., Cao, Z.: Efficient IBE with tight reduction to standard assumption in the multi-challenge setting. In: Cheon, J.H., Takagi, T. (eds.) ASIACRYPT 2016. LNCS, vol. 10032, pp. 624–654. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53890-6_21
Groth, J.: Simulation-sound NIZK proofs for a practical language and constant size group signatures. In: Lai, X., Chen, K. (eds.) ASIACRYPT 2006. LNCS, vol. 4284, pp. 444–459. Springer, Heidelberg (2006). https://doi.org/10.1007/11935230_29
Groth, J., Sahai, A.: Efficient noninteractive proof systems for bilinear groups. SIAM J. Comput. 41(5), 1193–1232 (2012)
Han, S., Liu, S., Qin, B., Gu, D.: Tightly CCA-secure identity-based encryption with ciphertext pseudorandomness. Designs, Codes and Cryptography 86(3), 517–554 (2018). https://doi.org/10.1007/s10623-017-0339-3
Hesse, J., Hofheinz, D., Kohl, L.: On tightly secure non-interactive key exchange. In: Shacham, H., Boldyreva, A. (eds.) CRYPTO 2018. LNCS, vol. 10992, pp. 65–94. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-96881-0_3
Hofheinz, D.: Algebraic partitioning: fully compact and (almost) tightly secure cryptography. In: Kushilevitz, E., Malkin, T. (eds.) TCC 2016. LNCS, vol. 9562, pp. 251–281. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49096-9_11
Hofheinz, D.: Adaptive partitioning. In: Coron, J.-S., Nielsen, J.B. (eds.) EUROCRYPT 2017. LNCS, vol. 10212, pp. 489–518. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-56617-7_17
Hofheinz, D., Jager, T.: Tightly secure signatures and public-key encryption. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 590–607. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-32009-5_35
Hofheinz, D., Kiltz, E.: Secure hybrid encryption from weakened key encapsulation. In: Menezes, A. (ed.) CRYPTO 2007. LNCS, vol. 4622, pp. 553–571. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-74143-5_31
Hofheinz, D., Koch, J., Striecks, C.: Identity-based encryption with (almost) tight security in the multi-instance, multi-ciphertext setting. In: Katz, J. (ed.) PKC 2015. LNCS, vol. 9020, pp. 799–822. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46447-2_36
Jutla, C.S., Ohkubo, M., Roy, A.: Improved (almost) tightly-secure structure-preserving signatures. In: Abdalla, M., Dahab, R. (eds.) PKC 2018. LNCS, vol. 10770, pp. 123–152. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-76581-5_5
Jutla, C.S., Roy, A.: Shorter quasi-adaptive NIZK proofs for linear subspaces. In: Sako, K., Sarkar, P. (eds.) ASIACRYPT 2013. LNCS, vol. 8269, pp. 1–20. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-42033-7_1
Kiltz, E., Wee, H.: Quasi-adaptive NIZK for linear subspaces revisited. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015. LNCS, vol. 9057, pp. 101–128. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46803-6_4
Kurosawa, K., Desmedt, Y.: A new paradigm of hybrid encryption scheme. In: Franklin, M. (ed.) CRYPTO 2004. LNCS, vol. 3152, pp. 426–442. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-28628-8_26
Lewko, A., Waters, B.: Why proving HIBE systems secure is difficult. In: Nguyen, P.Q., Oswald, E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 58–76. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-55220-5_4
Libert, B., Joye, M., Yung, M., Peters, T.: Concise multi-challenge CCA-secure encryption and signatures with almost tight security. In: Sarkar, P., Iwata, T. (eds.) ASIACRYPT 2014. LNCS, vol. 8874, pp. 1–21. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-45608-8_1
Libert, B., Peters, T., Joye, M., Yung, M.: Compactly hiding linear spans. In: Iwata, T., Cheon, J.H. (eds.) ASIACRYPT 2015. LNCS, vol. 9452, pp. 681–707. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48797-6_28
Morillo, P., Ràfols, C., Villar, J.L.: The kernel matrix Diffie-Hellman assumption. In: Cheon, J.H., Takagi, T. (eds.) ASIACRYPT 2016. LNCS, vol. 10031, pp. 729–758. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53887-6_27
Naor, M., Reingold, O.: Number-theoretic constructions of efficient pseudo-random functions. In: 38th FOCS, pp. 458–467. IEEE Computer Society Press, October 1997
Naor, M., Yung, M.: Public-key cryptosystems provably secure against chosen ciphertext attacks. In: 22nd ACM STOC, pp. 427–437. ACM Press, May 1990
Shoup, V., Shoup, V.: Why chosen ciphertext security matters. IBM research report RZ 3076 (1998)
Wang, Y., Matsuda, T., Hanaoka, G., Tanaka, K.: Memory lower bounds of reductions revisited. In: Nielsen, J.B., Rijmen, V. (eds.) EUROCRYPT 2018. LNCS, vol. 10820, pp. 61–90. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-78381-9_3
Acknowledgments
We thank the anonymous reviewers for their comments and, in particular, for pointing a problem in our definition of unbounded simulation soundness, and one in the proof of Theorem 4 in a previous version of this paper. The first author was supported by ERC Project PREP-CRYPTO (724307) and DFG grants (HO 4534/4-1, HO 4534/2-2), the second author was supported by the National Nature Science Foundation of China (Nos. 61502484, 61572495, 61772515), the Fundamental theory and cutting edge technology Research Program of Institute of Information Engineering, CAS (Grant No. Y7Z0291103) and the National Cryptography Development Fund (No. MMJJ20170116), and the third author was supported by the DFG grant (HO 4534/4-1). This work was done while the second author was visiting KIT. The visit was supported by China Scholarship Council.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 International Association for Cryptologic Research
About this paper
Cite this paper
Hofheinz, D., Jia, D., Pan, J. (2018). Identity-Based Encryption Tightly Secure Under Chosen-Ciphertext Attacks. In: Peyrin, T., Galbraith, S. (eds) Advances in Cryptology – ASIACRYPT 2018. ASIACRYPT 2018. Lecture Notes in Computer Science(), vol 11273. Springer, Cham. https://doi.org/10.1007/978-3-030-03329-3_7
Download citation
DOI: https://doi.org/10.1007/978-3-030-03329-3_7
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-03328-6
Online ISBN: 978-3-030-03329-3
eBook Packages: Computer ScienceComputer Science (R0)


 , where
, where 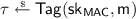 , where
, where  is computed as
is computed as 


 for defining
for defining 




 interpolating between
interpolating between 
 interpolating between
interpolating between 


 for defining
for defining 
 . Gray instructions are only executed in
. Gray instructions are only executed in
 .
.


 with oracle access to
with oracle access to
 of the
of the  cannot break the
cannot break the  can ask such a query with
can ask such a query with  . More precisely, we have
. More precisely, we have  can output a
can output a  .
.
 (with access to oracles
(with access to oracles 