Abstract
In this chapter, we will introduce the interval domain \(\mathbb {I\hspace {1.1pt} R}\), which is a topological space that represents the line of time in our work to come. The points of this space can be thought of as compact intervals [a, b] in \(\mathbb {R}\). The specialization order on points gives \(\mathbb {R}\) a non-trivial poset structure—in fact it is a domain—and as such it is far from Hausdorff.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
(0, 1)-sheaves are also sometimes called ideals, but this terminology clashes with two other notions we use in this book that are also called ideals—namely, ideals in a poset and rounded ideals in a predomain (see Definitions 2.5 and A.6)—thus we call them (0, 1)-sheaves to avoid confusion.
- 2.
- 3.
Throughout this book, we often use d or δ to stand for “down” and u or υ (upsilon) to stand for “up.”
- 4.
We will neither need this nor prove this, but
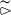 is the largest coverage for which I is a sheaf.
is the largest coverage for which I is a sheaf.
References
Ferrari, L.: Dyck algebras, interval temporal logic, and posets of intervals. SIAM J. Discrete Math. 30, 1918–1937 (2016)
Gierz, G., et al.: Continuous Lattices and Domains. Encyclopedia of Mathematics and Its Applications, vol. 93, pp. xxxvi+ 591. Cambridge University Press, Cambridge (2003). ISBN:0-521-80338-1. http://dx.doi.org/10.1017/CBO9780511542725
Johnstone, P., Joyal, A.: Continuous categories and exponentiable toposes. J. Pure Appl. Algebra 25(3), 255–296 (1982). ISSN:0022-4049. http://dx.doi.org/10.1016/0022-4049(82)90083-4
Johnstone, P.T.: Sketches of an Elephant: A Topos Theory Compendium. Oxford Logic Guides, vol. 43, pp. xxii+ 468+ 71. New York: The Clarendon Press/Oxford University Press (2002). ISBN:0-19-853425-6
Posite. https://ncatlab.org/nlab/show/posite (visited on 06/02/2017)
Shulman, M. Exact completions and small sheaves. Theory Appl. Categ. 27, 97–173 (2012). ISSN:1201-561X
Author information
Authors and Affiliations
Rights and permissions
Copyright information
© 2019 The Author(s)
About this chapter
Cite this chapter
Schultz, P., Spivak, D.I. (2019). The Interval Domain. In: Temporal Type Theory. Progress in Computer Science and Applied Logic, vol 29. Birkhäuser, Cham. https://doi.org/10.1007/978-3-030-00704-1_2
Download citation
DOI: https://doi.org/10.1007/978-3-030-00704-1_2
Published:
Publisher Name: Birkhäuser, Cham
Print ISBN: 978-3-030-00703-4
Online ISBN: 978-3-030-00704-1
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)


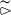 is the largest coverage for which I is a sheaf.
is the largest coverage for which I is a sheaf.