A Monte Carlo Framework for Denoising and Missing Wedge Reconstruction in Cryo-electron Tomography

Abstract

We propose a statistical method to address an important issue in cryo electron tomography image analysis: reduction of a high amount of noise and artifacts due to the presence of a missing wedge (MW) in the spectral domain. The method takes as an input a 3D tomogram derived from limited-angle tomography, and gives as an output a 3D denoised and artifact compensated tomogram. The artifact compensation is achieved by filling up the MW with meaningful information. The method can be used to enhance visualization or as a pre-processing step for image analysis, including segmentation and classification. Results are presented for both synthetic and experimental data.

1 Introduction

Cryo electron tomography (cryo-ET) is intended to explore the structure of an entire cell and constitutes a rapidly growing field in biology. The particularity of cryo-ET is that it is able to produce near to atomic resolution three-dimensional views of vitrified samples, which allows observing the structure of molecular complexes (e.g. ribosomes) in their physiological environment. This precious insight in the mechanism of a cell comes with a cost: i/ due to the low dose of electrons used to preserve specimen integrity during image acquisition, the amount of noise is very high; ii/ due to technical limitations of the microscope, complete tilting of the sample (180$^\circ$) is impossible, resulting into a blind spot. In other words, projections are not available for a determined angle range, hence the term “limited angle tomography”. This blind spot is observable in the Fourier domain, where the missing projections appear as a missing wedge (MW). This separates the Fourier spectrum into: the sampled region (SR) and the unsampled regions (MW). The sharp transition between these two regions is responsible for a Gibbs-like phenomenon: ray- and side-artifacts emanate from high contrast objects (see Fig. 1), which can hide important structural features in the image. Another type of artifact arises from the incomplete angular sampling: objects appear elongated in the blind spot’s direction (see Fig. 1). This elongation erases boundaries and makes it difficult to differentiate neighboring features.

Filling up the MW with relevant data can reduce or completely suppress these artifacts. Experimentally this can partially be done using dual-axis tomography [4], where the sample is tilted with respect to the second axis. Consequently the blind spot is smaller and the MW becomes a missing pyramid, which results into a smaller missing spectrum. In practice dual-axis tomography is technically more difficult to achieve and requires intensive post-processing in order to correct tilt and movement bias in the microscope. Another strategy consists in exploiting the symmetry of the observed structure to fill up the MW [3], but this can only be applicable to specific structures (e.g. virus). Another technique consists in combining several images, each containing a different instance of the same object, but with distinct blind spots. This technique is routinely used in cryo-ET and is known as sub-tomogram averaging [3], but it relies on the acquisition of several views of the same object type. Accordingly, edicated tomographic reconstruction algorithms have also been proposed, to compensate MW artifacts by using a regularization term [7, 10] and exploiting prior information. A simpler way of handling MW artifacts is described in [6], where a spectral filter is used to smooth out the transition between the SR and the MW. This filter is thus able to reduce ray- and side-artifacts, but the object elongation remains.

In this paper, we propose a stochastic method inspired from [2] for restoring 2D images and adapted to 3D in [9], and re-interpret the method to recover the MW in cryo-ET from a Monte Carlo (MC) sampling perspective. The method [9] has been shown to successfully recover missing regions in the Fourier domain, achieving excellent results for several missing region shapes, including the MW shape. The method [9] works by alternatively adding noise into the missing region and applying a patch-based denoising algorithm (BM4D). However, the method has no clear theoretical framework and appears therefore empirical. The authors interpret their method as a compressed sensing algorithm, which relies on two conditions: sparsity of the signal in some transform, and the incoherence between this transform and the sampling matrix. Actually, BM4D does rely on a transform where the signal is sparse. Nevertheless, it is not clearly established that this transform is incoherent with the sampling matrix, defined by the support of the SR. Therefore, there is no theoretical proof of convergence, even though the authors show numerical convergence. Also, the data in [9] is exclusively synthetic and corrupted with white Gaussian noise, for which BM4D has been well designed. It remains unclear how the method performs with experimental data and non Gaussian noise.

Consequently, we reformulate the method [9] as a Metropolis-Hastings procedure in the MCMC framework (Sect. 2), and demonstrate that it performs as well as the original method but converges faster. Moreover, any patch-based denoiser can be applied [5, 8, 9] and the concept is more general than [9]. Finally, we provide evidence that our method enhances signal in experimental cryo electron tomography images (Sect. 3).

2 Statistical and Computational Approach

Formally, we denote Y the n-dimensional noisy image, and $X\in \mathbb {R}^n$ the unknown image where $n=|\varOmega |$ is the number of pixels of the volume $\varOmega$. We consider the following observation model:

$$\begin{aligned} Y = \mathcal {M}( X + \eta ) \end{aligned}$$

(1)

where $\eta \sim \mathcal {N}(0,I_{n\times n} \sigma _e^2)$ is a white Gaussian noise, $I_{n\times n}$ is the n-dimensional identity matrix, and $\mathcal {M}(.)$ is an operator setting to zero the Fourier coefficients belonging to the MW support.

To recover the unknown image, we propose a dedicated Monte-Carlo sampling procedure that generates at each iteration k a sample $\hat{X}_k\in \mathbb {R}^n$ (see Fig. 2). This procedure is based on the Metropolis-Hastings algorithm, determined by two steps: i/ a proposal step, where a n-dimensional candidate image is generated from a proposal distribution; ii/ an evaluation step, where the candidate is either accepted or rejected according to the Gibbs energy $E(\hat{X}_k)$, defined as the $l_2$ norm between the candidate $\hat{X}_k$ and the observed image Y:

$$\begin{aligned} E(\hat{X}_k) = \parallel \mathcal {M}(Y) - \mathcal {M}(\hat{X}_k) \parallel ^2. \end{aligned}$$

(2)

In addition, we compute the norm on the SR support only, given that the MW of Y contains no information.

Formally, the procedure is defined as follows:

• 1. PROPOSAL STEP:

  • Perturbation: we perturb the current $\hat{X}_k$ with a n-dimensional white Gaussian noise with variance $\sigma _p^2$: $\hat{X}_{k}^{\epsilon } = \hat{X}_{k} + \epsilon$, with $\epsilon \sim \mathcal {N}(0, I_{n\times n} \sigma _p^2)$.

  • Projection: we project $\hat{X}_{k}^{\epsilon }$ on the subspace of images having the same observed frequencies as Y: $\varPi (\hat{X}_k^{\epsilon }) = \text {FT}^{-1}( I_{S}\times \text {FT}(Y)) + (1-I_{S})\times \text {FT}(\hat{X}_{k}^{\epsilon }) )$ where FT denotes the Fourier transform, and $I_S$ is a binary mask having values of 1 for Fourier coefficients belonging to the SR and values of 0 otherwise.

  • Denoising: $DN(\varPi (\hat{X}_k^{\epsilon })) = \tilde{X}_k$.

• 2. EVALUATION STEP:

  Define $\hat{X}_{k+1}$ as:

  $$\begin{aligned} \hat{X}_{k} = \left\{ \begin{array}{ll} \tilde{X}_{k} &{} \text{ if } \alpha \le \exp {\dfrac{-\varDelta E(\tilde{X}_{k},\hat{X}_{k-1})}{\beta }}, \\ \hat{X}_{k-1} &{} \text{ otherwise }, \end{array} \right. \end{aligned}$$

  (3)

  where $\alpha$ is a random variable: $\alpha \sim U[0,1]$ (uniform distribution), $\beta >0$ is a scaling parameter and $\varDelta E(\tilde{X}_{k},\hat{X}_{k-1}) = E(\tilde{X}_{k}) - E(\hat{X}_{k-1})$

Actually, the originality of our approach lies in the way the candidates are proposed. The objective is to explore a subset $\mathcal {S}$ of plausible images, $\mathcal {S}$ being shaped by our prior knowledge. The perturbation allows to randomly explore the image space around $\hat{X}_k$, applying the prior guaranties that the exploration is limited to $\mathcal {S}$. The prior is twofold: i/ the images should have the same SR as Y, hence the projection operation; ii/ the images should be piece-wise smooth and self-similar, hence the patch-based denoising.

In the Bayesian framework, we focus on the conditional expectation estimator, computed as the average of N generated samples $\hat{X}_k$:

$$\begin{aligned} \hat{X} = \lim _{N\rightarrow \infty } \frac{1}{N-N_b} \sum _{k=N_b}^{N} \hat{X}_k \simeq \frac{1}{Z} \sum _{\lambda =1}^{M} e^{-E(X_{\lambda })} X_{\lambda } \end{aligned}$$

(4)

where Z is a normalization constant and M is the cardinal of the space $\mathcal {S}$ of admissible images. It is recommended to introduce a burn-in phase to get a more satisfying estimator. Hence, the first $N_b$ samples are discarded in the average $\hat{X}$.

In the end, the method is governed by three parameters: the number of iterations N, the noise variance $\sigma ^2_{n}$ and the scaling parameter $\beta$. At each iteration k, the patch-based denoising algorithm removes the perturbation noise $\epsilon$. The parameter $\beta$ affects the acceptance rate of the evaluation step. The higher the value of $\beta$, the higher the acceptance rate. For a high enough $\beta$ value, all proposed samples are accepted and we fall back on the original method [9]. This method cannot retrieve unobserved data, but it merely makes the best statistical guess of what the missing data could be, based on what has been observed.

This iterative procedure is successful provided that the denoising algorithm is able to remove the perturbation noise. In practice, the perturbation noise is Gaussian, as most of state-of-the-art denoising algorithm assume additive white Gaussian noise. This also means that any performant denoising algorithms including BM4D can be used in this framework [1, 5, 8]. Depending on the image contents and modality, some denoising methods could be more adapted than others, given their particular properties and assumptions.

3 Experimental Results

In this section, we present the results when the denoising is performed by using BM4D and $\sigma _e=\sigma _n$ in order to compare to [9]. We considered $N=1000$ iterations and a burn-in phase of $K_b=100$ iterations. Similar results have been obtained with the patch-based denoiser NL-Bayes [8].

Data Description. Three data sets (A, B and C) have been used to evaluate the performance of the method. Dataset A has been simulated, and consists of a density map of the 20S proteasome, first corrupted by adding varying amount of noise and then by applying artificially the MW (by giving zero-values to Fourier coefficients using a wedge shaped mask). Dataset B is an experimental sub-tomogram containing a gold particle. Dataset C is an experimental sub-tomogram containing 80S ribosomes attached to a membrane.

Evaluation Procedure. The evaluation differs depending on the dataset. For dataset A we have at our disposal a ground truth. We can thus use similarity measures like the PSNR (peak signal to noise ratio) for evaluation. In dataset B, we see that the gold particle is elongated (ellipse) due to the MW artefacts. Improving the sphericity of the object is thus a good evaluation criterion. For dataset C, we measure the similarity between the central ribosome and a reference (obtained via sub-tomogram averaging). The evaluation criterion is the Fourier shell correlation (FSC), commonly used in cryo-ET [11]. In order to measure the quality of the recovered MW only, we also compute the FSC over the MW support (“constrained” FSC or cFSC).

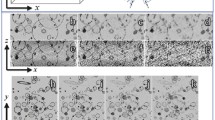
Results and Discussion. From the results on dataset A (Fig. 3(a)) it can be seen how well the method works in the absence of noise ($\sigma _{n}=0$): a quasi perfect image recovery has been achieved, despite the complexity of the object. Increasing the amount of noise deteriorates the performance, but as can be observed for $\sigma _{n}=0.2$ the result is still satisfying. For high amounts of noise ($\sigma _{n}=0.4$), the object contrast is still greatly enhanced but the MW artifacts could not be completely removed. Let us examine the Fourier domain (Fig. 3(b)): in the absence of noise, the MW has been filled up completely, whereas for an increasing amount of noise the MW reconstruction is increasingly restrained to the low frequencies. This is because high frequency components of a signal are more affected by noise, which makes them more difficult to recover. In Fig. 3(c), the evolution of the PSNR over time shows that the method converges to a stable solution. In Fig. 3(d) we compare our method to the original one [9]. Both methods produce visually identical results in the spatial domain, as well as in the spectral domain, as can be confirmed by the final achieved PSNR values. However, the difference lies in convergence speed: our method takes about half as long as the original method [9]. Even though the synthetic dataset A is a simplified case of data corruption in cryo-EM, it gives a good intuition of the method performance.

The result on dataset B shows that noise is reduced and a significant part of the MW could be recovered (see Fig. 1). Even though the recovery is not complete, it is enough to reduce the MW artifacts while preserving and enhancing image details. The ray and side artifacts induced by the high contrast of the gold particle are reduced and its sphericity has been improved, bringing the image closer to the expected object shape. The result on this dataset shows that the method is able to handle experimental noise in cryo-ET.

Fig. 1.

Experimental sub-tomogram ($61\,\times \,61\,\times \,61$ voxels) containing a gold particle (dataset B). The top row shows the input in the spectral and spatial domains, the bottom row shows the output.

Fig. 2.

The method flowchart. The $1^{st}$ icon row represents the data in the spectral domain, the $2^{nd}$ in the spatial domain.

Fig. 3.

Simulated data of the 20 S proteasome, for varying amounts of noise (dataset A). All images depict ortho-slices of 3D volumes. The volume size is $64\times 64\times 64$ voxels. For (a) and (b), top row: method inputs, bottom row: method outputs. Results are shown in the spatial domain (a) and in the spectral domain (b). In (c) can be observed the ground truth and the evolution of the PSNR over iterations. Finally, in (d) we compare our method to the orginal method described in [9]

Fig. 4.

Experimental sub-tomogram ($46\,\times \,46\,\times \,46$ voxels) containing ribosomes attached to a membrane (dataset C). (a) Top row: input image in spectral domain, spatial domain and 3D view of the thresholded data. Bottom row: the same representations for the output. (b) FSC and cFSC measures of the method input (in black) and output (in red). All measures are wrt the same reference. (Color figure online)

The dataset C contains molecules (ribosomes) that have more interest for biologists (see Fig. 4). This case is more challenging, because the objects have a more complex shape and less contrast, i.e. the SNR is lower. Nonetheless, the method could enhance the contrast and according to the FSC criteria, the signal has indeed been improved. Although visually it is more difficult to conclude that the MW artifacts have been affected, the Fourier spectrum shows that Fourier coefficients could be recovered. With no surprise, the amount of recovered high frequencies is less than for dataset B, because of the lower SNR. It is now necessary to provide a proof that the recovered coefficients carry a coherent signal, therefore the cFSC has been measured. The black curve in Fig. 4 depicts the cFSC between the unprocessed image and the reference: given that the MW contains no information, the curve represents noise correlation. Consequently, everything above the black curve is signal, which is indeed the case for the processed data (red curve in Fig. 4). To illustrate how the method can improve visualization, a simple thresholding has been performed on the data (3D views in Fig. 4). While it is difficult to distinguish objects in the unprocessed data, the shape of ribosomes become clearly visible and it can be observed how they are fixated to the membrane.

4 Conclusion

We have proposed a Monte-Carlo simulation method to denoise and compensate MW artifacts in cryo-ET images. Any patch-based denoiser can be used in this framework and the procedure converges faster than [9]. Our experiments on both synthetic and experimental data show that even for high amounts of noise, the method is able to enhance the signal. However, the method needs a reasonable constrast of the object of interest to perform well, which is not always the case in cryo-ET. Nevertheless, with improving electron microscopy techniques like direct electron detection sensors and phase contrast methods, the method will be able to produce even more impressive results. The effectiveness of the method being demonstrated for the challenging case of cryo-ET, the method can be applied to other imaging modalities, especially on images with high SNR values.