In Heck and Erdfelder (2016), we proposed a general approach that extends multinomial processing tree (MPT) models to measure the relative speed of cognitive processes (see Heck et al., 2018b, for an alternative, parametric approach). The development of a general model class that combines MPTs with response times (RTs) is important given the diverse applications of MPT models, many of which are associated with ordinal response time predictions for processing sequences (Erdfelder et al., 2009). In his reply, Starns (2018) criticized the lack of a parameter representing speed–accuracy trade-off in an example we presented, the RT-extended two-high-threshold (2HT-RT) model. To address this problem, he proposed a novel model tailored to capture the speed–accuracy trade-off in a specific paradigm (yes-no recognition) assuming a specific mechanism (a race of detection and guessing processes) with specific parametric assumptions for the processing times involved (ex-Gaussian distributions, i.e., distributions of the sum of an exponential and an independent normal random variable). By doing so, Starns often referred to “the Heck & Erdfelder (2016) model” (emphasis added) without distinguishing between the 2HT-RT model and the general MPT-RT model class we proposed. Even though the former term may facilitate the distinction between different extensions of the two-high-threshold model to RTs (e.g., see Klauer and Kellen, 2018, for a more recent approach), it also bears the danger of ignoring the conceptual difference between the specific 2HT-RT model we used as an example and the general model class advanced in our original paper.

In this reply, we highlight important differences between the overarching goals and purposes of the general MPT-RT model class and the narrower aims of specific process models such as those designed to represent speed–accuracy trade-offs.Footnote 1 Moreover, we show that, if desired and necessary, the proposed class of MPT-RT models can accommodate speed–accuracy trade-off in principle and even measure it by specific parameters. We highlight commonalities and differences between the race model proposed by Starns (2018) and an analogous MPT-RT model that also captures speed–accuracy trade-off and is motivated by the pioneering fast-guess model (Ollman, 1966; Yellott, 1971). Using Monte Carlo simulations, we show that the fast-guess model can approximate the race model quite well under specific conditions without being overly flexible. Following a discussion of criteria for choice between models, we also discuss potential limitations of the proposed model class and point to alternative modeling approaches.

MPT-RTs as a general-purpose model class

As elaborated in Heck and Erdfelder (2016), the proposed class of MPT-RTs has several advantages compared to specific process models (including the race model), some of which are acknowledged by Starns (2018, e.g., p. 2414 and 2416). First, MPT-RTs can be applied to a variety of paradigms and combined with existing MPT models relatively easily without the need to make parametric assumptions about latent response time distributions. For instance, Brainerd, Nakamura, and Lee (2019) recently developed an MPT-RT model for the conjoint recognition paradigm to test whether familiarity is faster than context recollection. Instead of indirectly inferring the relative speed of different latent processes from speed–accuracy functions, Brainerd et al.’s innovative MPT-RT model aims at testing relative latency predictions derived from dual-recollection theory directly (Brainerd, Gomes, & Moran, 2014).

Of course, the assumption of a latent race between detection and guessing processes proposed by Starns (2018) for the yes-no recognition task can in principle also be generalized to other paradigms and combined with MPT models that assume more than two latent states. However, such developments will pose major theoretical questions, for instance, which processes actually race against each other and which do not, Footnote 2 let alone the problem of specifying appropriate continuous distributions for the latent processing times involved. Moreover, application and evaluation of such models is technically more complex and requires a strong background in statistical programming.Footnote 3 In contrast, because MPT-RTs are nothing else but a special subclass of standard MPT models (for MPTs, see Batchelder and Riefer, 1999; Erdfelder et al., 2009; Hu & Batchelder, 1994), MPT-RTs can be fitted with standard software for MPT modeling (e.g., Heck, Arnold, & Arnold, 2018a; Moshagen, 2010; Singmann & Kellen, 2013), thus making it more likely that substantive and applied researchers incorporate information about the speed of processes in their MPT models instead of ignoring RTs entirely. Adding to these practical advantages, Heck and Erdfelder (2016) proved formal strategies that allow checking the identifiability of a new MPT-RT model, that is, whether the parameters are uniquely determined by the data. In contrast, comparable analytic strategies to assess the identifiability of specific process models such as Starn’s race model are currently lacking, and hence, model development, refinement, and testing are more complex.

Second, given that many psychological theories currently do not make precise parametric predictions, MPT-RTs allow testing core assumptions of a theory (e.g., about the order of latent processes) without requiring auxiliary parametric assumptions (e.g., Brainerd et al., 2019; Heck & Erdfelder, 2017). If one is willing to commit to parametric assumptions, Starns (2018) showed that a race mechanism for speed–accuracy trade-offs can be implemented, for example, by assuming ex-Gaussian distributions for the latent processing times. However, this in turn means that any “correction for incautious responding” based on the proposed race model depends on the auxiliary parametric assumptions. Put differently, the estimated “caution-corrected detection probability” DAV will differ depending on the types of distributions assumed for the latent processes since these parametric assumptions determine the speed–accuracy trade-off function. More generally, the process characterization of speed–accuracy trade-offs necessitates a strong theoretical commitment to a specific mechanism (a race, a diffusion process etc.), which is avoided when using the MPT-RT model class. Given the broad range of psychological domains in which MPT models have been applied, it seems unlikely that a single speed–accuracy mechanism applies to many diverse areas such as memory, social cognition, and decision making (Erdfelder et al., 2009; Hütter and Klauer, 2016). Moreover, even when focusing on a small subclass of paradigms such as two-alternative forced choice (2AFC) tasks, it is difficult to identify a single processing mechanism that fully accounts for the speed–accuracy trade-off. For the popular 2AFC diffusion model (Ratcliff & McKoon 2008; Ulrich, Schröter, Leuthold, & Birngruber, 2015; Voss, Nagler, & Lerche, 2013), for example, it has been shown that enforcing speeded decisions does not only decrease the decision threshold as expected (thus enforcing incautious responding) but unexpectedly also affects the drift rate of evidence accumulation (Rae, Heathcote, Donkin, Averell, & Brown, 2014).

Third, the main point of criticism of Starns (2018) is that “the Heck and Erdfelder (2016) model lacks a speed– accuracy mechanism” and thereby fails the “critical test for any RT model (⋯) to accommodate the speed–accuracy trade-off.” This argument takes it for granted that any formal modeling of response times in cognitive psychology necessarily requires parameters representing speed–accuracy trade-off. However, there are many examples of useful and successful RT models in psychology that focus on general processing mechanisms without considering or implementing speed–accuracy mechanisms, for instance, the additive factors method (Sternberg, 1969), system factorial technology (Townsend, 1984), and models for judgment and decision making (Glöckner & Betsch, 2008). Admittedly, many of these models often do not require a speed–accuracy mechanism because performance is at ceiling or because accuracy is not well defined. However, considering the variety of paradigms for which influential MPT models have been developed (Erdfelder et al., 2009), it is obvious that many of these paradigms lack a clear-cut accuracy criterion that is a prerequisite for modeling speed–accuracy trade-off (e.g., randomized response paradigms or social dilemma games; Klein, Hilbig, & Heck, 2017).

In MPT applications where responses can be classified as correct vs. incorrect, accuracy is usually incentivized and there is no response deadline. For such paradigms and experimental designs, in which speed–accuracy trade-offs are not expected to have any effects (e.g., when manipulating the item types in a recognition-memory experiment), it may still be of interest to test predictions of different theories on the relative speed of the cognitive processes involved. As already outlined above, Brainerd et al., (2019) recently used an MPT-RT model to evaluate predictions of the dual-recollection theory on the relative speed of familiarity, context recollection, and target recollection in the conjoint recognition paradigm. Moreover, in an application of MPT-RT models to probabilistic inferences (e.g., judgments on questions such as “which city is larger?”), Heck and Erdfelder (2017) showed that the RT-extended r-model (which is based on the r-model by Hilbig, Erdfelder, & Pohl, 2010) allows testing predictions of two process models against each other, and that existing data from different studies and labs suggest a clear winner. Importantly, Heck and Erdfelder (2017) also showed that both process models cannot be discriminated on the basis of response frequencies only. That is, whereas the standard r-model ignores RTs and thus cannot discriminate between the two process models, an MPT-RT extension of the r-model that includes RTs can.

These two recent examples already show that Starns’ generally framed statement “one critical test for any RT model is its ability to accommodate the speed–accuracy trade-off” (emphasis added) does not hold in full generality. RT models that do not account for speed–accuracy trade-offs can obviously still be useful and valuable to test psychological theories, especially if these theories assume multiple cognitive processes as in MPT modeling, and if responses are given with a clear-cut focus on accuracy. More generally, MPT models are mainly concerned with explaining response distributions by parameters that represent the probabilities of different underlying latent states or processes under specific experimental conditions. The validity of this approach does not hinge on any type of counterfactuals such as “how well could have someone performed if this person attempted to be more accurate?” In the 2HT-RT model, for example, an estimate such as \(\hat d_{o} = .70\) means that 70% of responses to old items were driven by a detection state. Whether this estimate could have been higher under some other condition is mostly irrelevant. What usually matters in typical MPT applications is what is happening in a given experimental condition, not in an “ideal” condition that was not observed. Footnote 4

Nevertheless, we agree that it is a benefit (although not a necessity) for RT models to make explicit and testable assumptions why and how much accuracy decreases when the focus is on speeded responding. For instance, a speed–accuracy trade-off mechanism is obviously required to capture effects of response deadlines and it should also be considered as a potential source of bias for other types of manipulations that might be confounded with (in)cautious responding. Are MPT-RTs useless when the goal is to account for effects of this sort? As discussed in the next section, this is not the case. MPT-RTs are sufficiently general to accommodate speed–accuracy trade-offs if researchers are interested in modeling data with response deadlines.

Modeling speed–accuracy trade-offs using MPT-RTs

In his reply, Starns (2018) proposes a novel discrete-state model for a standard recognition paradigm. Overall, we applaud the idea and effort to develop a discrete-state model that has a mechanism for speed–accuracy trade-offs. However, as mentioned above, the proposed “correction for incautious responding” builds heavily on the assumed race mechanism and the (auxiliary) parametric assumptions. Hence, before relying on this model, a careful empirical validation is necessary by showing that experimental manipulations selectively influence the parameters.

In Heck and Erdfelder (2016), we proposed and tested a RT-extended version of the two-high threshold model (2HT-RT) as an example of an MPT-RT model. This specific model aimed at modeling recognition memory when individuals are not under time pressure but have sufficient time to respond as accurately as possible. Importantly, the model never aimed at accounting for speed–accuracy trade-offs, but for the relative speed of detection and guessing processes in situations with a focus on accuracy. Consequently, the data we analyzed in Heck and Erdfelder (2016) were collected with explicit accuracy instructions and no response deadlines involved. As one of the main empirical results, we found that responses based on guessing were stochastically slower than detection responses. Notably, using the conjoint recognition procedure with a focus on accuracy, Brainerd et al., (2019) recently also found that responses involving guessingFootnote 5 were slower than either type of memory-based responses considered in their MPT-RT model.

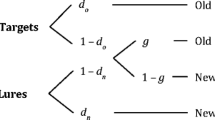
When the interest is in situations with a focus on accuracy only, the speed–accuracy mechanism proposed by Starns (2018) becomes less relevant. To illustrate this, we remind the reader that the race model by Starns (2018) distinguishes two detection probabilities D: The probability DAV that detection is in principle available due to successful encoding and the probability DAC that a tested item is actually detected (which requires that the detection process finishes before the guessing process). Essentially, the race model predicts that DAC = r ⋅ DAV, where r is a shrinkage factor between zero and one that quantifies the relative decrease in accuracy due to fast responding:

$$ r = \int \gamma_{G}(t) {\varGamma}_{D}(t) \text d t, $$
(1)

where γ and Γ are the density and cumulative distribution functions of the ex-Gaussian distribution, respectively, and the indices G and D represent the processes (i.e., Guessing vs. Detection) to which the latency distribution refers (for details, see Starns, 2018). Figure 1 shows that this factor r depends on the overlap of the two independent finishing time distributions of the detection and guessing process. If guessing is relatively slow compared to detection (e.g., if the mean parameters μ satisfy μG ≫ μD), it follows that detection usually succeeds, implying that r ≈ 1 and DAC ≈ DAV. Hence, in high-accuracy conditions, the standard 2HT-RT model for accuracy conditions (shown in Fig. 2A) provides estimates for DAC = do that approximate the parameter DAV of the race model. Empirically, this assumption is justified by our finding that guessing is stochastically slower than detection when the focus is on accuracy (Heck and Erdfelder, 2016). Only when the finishing times of guessing are similar to or even faster than those of detection (i.e., in situations with a focus on speed), the shrinkage factor r drops substantially below one (cf. Figure 1).

Fig. 1
figure 1

a Ex-Gaussian distributions assumed for the latent processes in the race model by Starns (2018). b Implied shrinkage factor (i.e., speed–accuracy function) for the probability of available detection DAV

Full size image
Fig. 2
figure 2

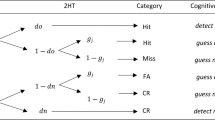
a Original version of the RT-extended two-high threshold model (Heck and Erdfelder, 2016). b Fast-guess extension of the 2HT-RT model motivated by the fast-guess model (Yellott, 1971). The model parameters refer to the probability of detecting an old item (do), guessing ‘old’ (g), or making a fast guess (f ). The corresponding probabilities of responding faster than a predetermined RT boundary for these three processes are labeled Ld, Lg, and Lf, respectively. Responses due to target detection (as opposed to guessing) are highlighted with solid boxes

Full size image

If the interest is in modeling data from both accuracy and speed conditions, MPT-RTs can in principle still be developed based on the core idea of the now classical fast-guess model (Ollman, 1966; Yellott, 1971). The fast-guess model assumes that observed responses emerge as a mixture of fast, stimulus-independent guesses and slower, stimulus-dependent responses. Figure 2B shows how this simple idea allows to generalize the 2HT-RT model to account for speeded responding: In addition to the two latent states of the original 2HTM (i.e., guessing and detection), we assume a third state representing fast guessing. This is in line with Starns’ (2018; p. 8) assumption that “psychologically, this means that, on each trial, participants commit to guessing ‘old’ or ‘new’ at some point relatively early in the trial.” Hence, a certain proportion f of responses and RTs is merely due to fast guessing and results in correct ‘old’ responses with probability g. Importantly, the model assumes that stimulus-independent fast guesses result in a different distribution of RTs than slow guesses following detection failure, as indicated by the distinct latency parameters Lf and Lg, respectively. If the model is fitted to data from a speed and an accuracy condition jointly, the model is identified when assuming that fast guessing does not affect responding in the accuracy condition, facc = 0 (which is justified by our observation that the shrinkage factor for the detection probability is r ≈ 1 when the focus is on accuracy).

Interestingly, the proposed fast-guess extension of the 2HT-RT model resembles the race model by Starns (2018) in that guessing results in a decrease of the probability of detection do by the shrinkage factor r = 1 − f. Hence, both models predict that the probability of available detection decreases in the speed condition to do ⋅ r. However, the proposed fast-guess model predicts a constant shrinkage factor r that does not depend on the relative speed of latent detection and guessing processes as in the race model (cf. Eq. 1).

Importantly, it is possible to test empirically whether the shrinkage factor is constant or not—even without modeling RTs parametrically. For this purpose, consider a 2 × 2 design of memory strength (weak vs. strong) and testing context (focus on speed vs. accuracy). Assuming that memory strength does not affect the probability of fast guesses, the fast-guess model would predict that the decrease from do to do ⋅ r between the accuracy and speed conditions is identical for the strong and the weak memory conditions (i.e., rstrong = rweak). In contrast, when assuming that better memory leads to faster detection times, the race model would predict that rstrong > rweak, since detection succeeds more often when it becomes faster relative to guessing (cf. Figure 1). Hence, we have derived a critical test between two distinct mechanisms for speed–accuracy trade-offs, that is, stimulus-independent fast guesses (Yellott, 1971) vs. a latent race between detection and guessing (Starns, 2018). More generally, these considerations show that the MPT-RT model class is useful for deriving and testing assumptions about speed–accuracy trade-offs, even though the specific model tested in Heck and Erdfelder (2016) did not include a mechanism for this purpose.

The fast-guess 2HT-RT model as a nonparametric approximation of the race model

The proposed fast-guess extension of the 2HT-RT model makes different predictions than Starns’ race model in general and should thus best be considered as an alternative (nonparametric) approach to model speed–accuracy trade-off in yes-no recognition tasks. Notwithstanding this fact, one might still be interested in how well the fast-guess model can approximate data known to be perfectly in line with the race model. If such an approximation succeeds reasonably well under practically relevant context conditions, it seems defensible to use our fast-guess extension of the 2HT-RT model as a simple default measurement model to account for effects of response deadlines, even if the exact nature of the speed–accuracy trade-off mechanism (i.e., stimulus-independent fast guesses vs. race between detection and guessing) is not entirely clear.

To evaluate whether the fast-guess 2HT-RT model provides an acceptable approximation of Starns’ race model, we performed Monte Carlo simulations. We relied on simulations instead of analytical derivations since linking the two models analytically appeared to be intractable. Based on the R scripts provided by Starns (2018), we generated data from the race model for two conditions (speed vs. accuracy) each with two item types (target vs. lure). We simulated 250 replications with 1500 trials per condition (cf. Starns, 2018) and data-generating parameters that were similar to those of the original simulations: The probability parameters \(D^{\text {old}}_{AV}\), \(D^{\text {new}}_{AV}\), and g were drawn from uniform distributions on the interval [.20,.80]. The detection RTs followed an ex-Gaussian with random parameters mean μD ∈ [0.400,0.800], standard deviation \(\sigma _{D} \in [0.050, \min \limits (\mu _{D}/5)]\), and mean of the exponential component λD ∈ [0.100,0.333]. The speed–accuracy trade-off was modeled by a manipulation of the mean parameter of the ex-Gaussian for guessing responses, with fast guesses in the speed condition, \(\mu ^{\text {speed}}_{G} \in [\mu _{D} - 0.200,\mu _{D} +0.200]\), and slow guesses in the accuracy condition, \(\mu ^{\text {acc}}_{G} \in [\mu _{D} + 0.200,\mu _{D} +0.500]\). Moreover, the two guessing RT distributions were identical with respect to the standard deviation σG ∈ [σD − 0.020, σD + 0.020] and the mean of the exponential component λG ∈ [λD + 0, λD + 0.300].

In each replication, we fitted both the race model and the fast-guess model shown in Fig. 2 with two RT bins (using the geometric mean as RT boundary; Heck and Erdfelder 2016). As mentioned above, the latter model assumed that fast guesses do not occur in the accuracy condition (facc = 0), which renders the model identifiable. Figure 3 shows the recovery of this simulation, where the true, data-generating parameters are on the x-axis and the estimated parameters of the fast-guess model are on the y-axis. The results show that the fast-guess 2HT-RT model provides valid estimates of the two probabilities of available detection DAV for studied and new items, and also for the guessing probability g. Note that both detection probabilities are slightly underestimated (with an average difference of − .04). This is due to the shrinkage factor which is actually only close to one but not identical to one in the accuracy condition as assumed in our fast-guess model (cf. Fig. 1). Apart from this small expected bias, the model allows to measure differences in the parameters validly, as indicated by the high correlation between the estimated and the true parameters (rdo = .966, rdn = .974, and rg = .996). The fast-guess model also recovered the shrinkage factor r = 1 − f (cf. Eq. 1) quite well, the complement of the fast-guess probability (with a correlation of rr = .857). Moreover, the estimated order of the latent RT distributions was identical in all replications and followed the expected pattern that fast guesses were stochastically faster than detection responses, which in turn were stochastically faster than slow guesses (as reflected by the latency parameters Lf > LD > LG; for a detailed interpretation of these L parameters, see Heck & Erdfelder, 2016).

Fig. 3
figure 3

Correlation of the data-generating parameters of the race model (x-axis) with the estimates of the fast-guess 2HT-RT with two RT bins (y-axis)

Full size image

Of course, fitting Starns’ race model to the same data resulted in even higher correlations of the estimated and the true parameters (rdo = .982, rdn = .984, rg = .997, and rr = .980). However, this is not surprising given that the race model was in fact the data-generating model in our simulations. Its fit to the data thus cannot be exceeded by any other (factually misspecified) model such as the fast-guess 2HT-RT model. Overall, the simulation shows that the fast-guess version of the 2HT-RT may serve as an approximation of the race model without requiring any distributional assumptions on guessing and detection latencies. The approximation worked well under practically relevant conditions, that is, when finishing times of guessing in the accuracy condition were larger than those of detection (in which case the race model predicts a shrinkage factor r ≈ 1, meaning that almost all items that are in principle detectable are indeed detected; see Fig. 1). It is expected that the approximation quality will decrease if one cannot establish an accuracy condition in which fast guesses are very unlikely (i.e., f ≈ 0). In such a case, the assumption f = 0 required for the identifiability of the model will be violated. However, to investigate this issue in more detail for specific scenarios, one may adapt the simulation scripts that are available on the Open Science Framework (https://osf.io/qkfxz/). This notwithstanding, the present simulation results clearly showed that it is possible to construct MPT-RT models that can account for speed–accuracy trade-offs (based on the pioneering ideas of Ollman, 1966 and Yellott, 1971).

Model flexibility

A common concern regarding models with many parameters is overfitting, implying that MPT-RTs such as the proposed fast guess model may be overly flexible and thus be able to fit even random data. To rule out that the (parametric) race model is prone to overfitting, Starns (2018) assessed the model fit for distorted datasets that were obtained by adding an arbitrary constant to the model-generated RTs. Building on this idea, we ran a second simulation study to test whether the fast-guess 2HT-RT can fit even distorted datasets obtained by randomly permuting the model-generated frequencies (for a similar approach to assess MPT model flexibility see Erdfelder and Buchner, 1998). Based on the order constraint that fast guesses are stochastically faster than detection responses and slow guesses (i.e., Lf > Ld and Lf > Lg, we generated 100 frequencies for each item type and condition based on the fast-guess 2HT-RT with random parameter values in the interval [.20,.80]. Next, we randomly permuted the simulated frequencies for the “fast” and “slow” RT bins within each of the 8 original response categories of the 2HT model (e.g., for hits in the speed condition). This procedure induced between 0 to 8 permutations of the original data and only distorted those aspects of the data concerning the relative speed of responses (but not those concerning accuracy). Figure 4 shows the estimated statistical power of rejecting the fast-guess RT model based on a goodness-of-fit test G2(df = 5) and a significance level of α = 5%. Without permutations, the goodness-of-fit test adhered to the nominal significance level. However, if one or more of the RT frequencies were permuted, the test correctly rejected the null hypothesis with substantial power (1 − β > 65%), especially if 3–7 frequencies were permuted (1 − β > 87%). Moreover, random permutations affected the recovery of the memory parameters do and dn. Whereas the correlation between data-generating and estimated parameters was r = .74 for undistorted datasets, correlations dropped to values between r = .39 and r = .51 for 1 to 7 permutations (with a peak of r = .68 for eight permutations). Overall, the simulation thus shows that the fast-guess 2HT-RT is not overly flexible to fit arbitrary datasets with randomly permuted RT frequencies.

Fig. 4
figure 4

Statistical power of detecting between zero and eight random permutations of the RT frequencies within each response category of the 2HT model

Full size image

Choice between models

The decision which of the available modeling approaches is applied in empirical research should ultimately depend on specifics of the research question and a careful consideration of the benefits and drawbacks of each model class and the context conditions of the study. For example, consider the research question of separating accuracy and caution effects when only two conditions or groups are available (Starns, 2018, p. 2411). By assuming a specific mechanism and parametric shape of the speed–accuracy trade-off (cf. Figure 1B), the race model allows to test whether performance differences in two populations (e.g., between young and old adults) are due to differences in memory or due to incautious responding. In contrast, the incautious responding parameter f in the proposed fast-guess 2HT-RT model is not identifiable in a simple between-subjects design because the model does not assume a parametric speed–accuracy mechanism. Thus, the fast-guess model would be of no help for a two groups design. However, a simple extension of this model allows to test whether a focus on speed has different effects on young and old adults by implementing a 2 × 2 design with age as a between-subjects factor and speed vs. accuracy as a within-subjects factor. Based on this design and the assumption that one can establish an accuracy condition in which both young and old participants perform as best as possible (i.e., f = 0), one can test whether inducing a focus on speed has the same effect on the probability of fast guesses for both age groups (i.e., fyoung = fold).

This example highlights the general principle that different types of models enable researchers to test different types of research questions based on different sets of assumptions. Essentially, it depends on the substantive context whether researchers deem it to be easier to commit to a specific, parametric speed–accuracy mechanism or to other assumptions such as constraining a parameter to zero (e.g., f = 0) in certain experimental conditions. In the former case, parametric frameworks such as the race model proposed by Starns are valuable candidates to account for data that might be affected by speed–accuracy trade-offs. In the latter case, however, the proposed fast-guess 2HT-RT model may provide an alternative means of testing substantive hypotheses based on factorial experimental designs.

Ultimately, of course, the decision between both modeling approaches may also be made based on experimental data. If data are available for a 2 × 2 design with one factor manipulating speed vs. accuracy (e.g. short response deadline vs. no response deadline) and the other factor affecting Do selectively, then both the fast-guess 2HR-RT model and the race model can be fit to these data. By using the shrinkage factor criterion already outlined in the section on “Modeling speed–accuracy trade-offs using MPT-RTs” the better model for these data is easily identified.

Limitations

As in any modeling approach, both the fast-guess model and the MPT-RT model class in general come with limitations that should not be overlooked. We already outlined the major structural limitation of the fast-guess 2HT-RT model: It does not allow to separate accuracy and caution in simple two-conditions between-subjects designs. Hence, if only two conditions are available and an extension to a more complex experimental design is not feasible, it is necessary to commit to a specific processing mechanism such as the one assumed by the race model to account for possible differences in incautious responding between groups.

Looking at limitations of MPT-RT models in general, the probably most important issue that must be kept in mind concerns the nature of the “relative speeds” (or latencies) measured by these models. Strictly speaking, what is measured by MPT-RT models is the relative latency of a branch in an MPT model, that is, the overall duration of a sequence of cognitive processes or states represented by such a branch. To illustrate, when we measure the relative latency of responses based on guessing using the 2HT-RT model, we actually measure the relative duration of guessing “yes” (or ”no”, respectively) following detection failure in a recognition test (see the corresponding branches in Fig. 2A). When such a sequence of cognitive processes turns out to be relatively slow (or fast, respectively), MPT-RTs cannot determine uniquely whether this is due to the process resulting in detection failure, the process resulting in guessing “yes” or “no”, or both. Researchers interested in decomposing the total processing time of a branch into additive latencies for each component process involved need a different modeling approach such as the one originally proposed by Hu (2001) for the level of mean latencies and more recently elaborated to a new RT-MPT model family that allows to estimate the latency distributions of serial processing steps separately, including the option to test between different possible orders of the component processes (Klauer and Kellen, 2018). Of course, this surplus of information does not come for free: Complex parametric assumptions about the component latencies and their joint distribution are required to fit RT-MPT models. However, if a research question clearly aims at estimating the component latencies, we recommend to pay this price and switch from MPT-RT models (Heck & Erdfelder, 2016) to RT-MPT models (Klauer & Kellen, 2018).

Conclusions

Overall, we applaud the effort of Starns (2018) to develop a discrete-state model of recognition memory that includes a race mechanism of speed–accuracy trade-off. Whereas the race model aims at explaining a specific phenomenon for two-alternative choice tasks, MPT-RTs provide benefits as a broad class of general-purpose, simple-to-use models (Heck and Erdfelder, 2016). In this reply, we highlighted some of these advantages and also showed that MPT-RTs are sufficiently general to account for speed–accuracy trade-offs and allow for the derivation of novel critical tests between different ways of modeling speed–accuracy trade-off. We also showed that a specific MPT-RT—the fast-guess 2HT-RT model—may approximate Starns’ race model quite well under practically relevant conditions and can thus be used as a simple default model for speeded yes-no recognition tasks.

More generally, we want to stress again that RT models in general and MPT-RT models in particular can be useful even when they do not account for speed–accuracy trade-offs. Supporting this argument, Brainerd et al., (2019, p. 17) concluded that “we have seen how easily this new procedure [the MPT-RT approach by Heck and Erdfelder (2016)] generates latency extensions of existing cognitive models and how such an extension can deliver a rich assortment of novel findings on fundamental theoretical questions.” Evaluating any RT model or modeling approach with respect to merely one specific phenomenon that has been the focus of some (but definitely not all) research in cognitive psychology (i.e., the speed–accuracy trade-off) may give rise to a criticism of potentially powerful model families that have benefits for behavioral science as a whole.