Abstract
Gambling behavior presents a broad variety of individual differences, with a continuum ranging from nongamblers to pathological gamblers. The reward network has been proposed to be critical in gambling behavior, but little is known about the behavioral and neural mechanisms underlying individual differences that depend on gambling preference. The main goals of the present study were to explore brain oscillatory responses to gambling outcomes in regular gamblers and to assess differences between strategic gamblers, nonstrategic gamblers, and nongamblers. In all, 54 healthy volunteers participated in the study. Electroencephalography was recorded while participants were playing a slot machine task that delivered win, near-miss, and full-miss outcomes. Behaviorally, regular gamblers selected a larger percentage of risky bets, especially when they could select the image to play. The time–frequency results showed larger oscillatory theta power increases to near-misses and increased beta power to win outcomes for regular gamblers, as compared to nongamblers. Moreover, theta oscillatory activity after wins was only increased in nonstrategic gamblers, revealing differences between the two groups of gamblers. The present results reveal differences between regular gamblers and nongamblers in both their behavioral and neural responses to gambling outcomes. Moreover, the results suggest that different brain oscillatory mechanisms might underlie the studied gambling profiles, which might have implications for both basic and clinical studies.
Similar content being viewed by others
People get involved in gambling under many different circumstances. They may gamble to interact in a social event, to play or compete with others, to escape their problems, or merely to experience the arousing sensation of wagering and dreaming of a “big win” (Binde, 2005). Although most people enjoy gambling in a recreational manner, a small percentage of people (0.2%–2%; Kessler et al., 2008; Petry, Stinson, & Grant, 2005) develop gambling-related problems that affect their personal and interpersonal life. Risk factors such as the frequency, type, and variety of gambling, as well as comorbid disorders, may influence the progression to a gambling disorder (Breen & Zimmerman, 2002; Shen, Kairouz, Nadeau, & Robillard, 2015). In addition, the development of a gambling disorder has been related to a strong effect of cognitive biases and to abnormal processing of monetary outcomes. The most frequently reported cognitive biases related to gambling are illusion of control, which refers to the perception of control in situations in which no true control is possible (Goodie, 2005; Langer, 1975; Leotti & Delgado, 2011; Lorenz et al., 2015) and strong reactivity to near-miss events (NMs; Chase & Clark, 2010; Habib & Dixon, 2010; Ulrich & Hewig, 2014). NMs are situations in which an action yields a negative result but is very close to being successful. When compared to full-misses, NMs generate greater physiological arousal (Clark, Crooks, Clarke, Aitken, & Dunn, 2012) and increase the desire to continue gambling (Côté, Caron, Aubert, Desrochers, & Ladouceur, 2003), although a NM is objectively a loss. Moreover, NMs engage overlapping circuitry (Clark, Lawrence, Astley-Jones, & Gray, 2009) and evoke time–frequency patterns similar to those of wins (Alicart, Cucurell, Mas-Herrero, & Marco-Pallarés, 2015). Notably, the NM effect is enhanced in pathological gamblers, showing increased striatal sensitivity to NMs (Sescousse et al., 2016), which in turn correlates with gambling severity (Chase & Clark, 2010).
Traditionally, gambling activities are divided into strategic and nonstrategic. In nonstrategic or chance games, gamblers do not have any influence over the outcome (such as with slot machines or bingo), whereas in strategic or skill games (such as poker or sports betting), gamblers may use prior knowledge to improve their performance (Odlaug, Marsh, Kim, & Grant, 2011). Previous studies have shown that chance gamblers present a faster onset of problem gambling (Breen & Zimmerman, 2002), lower odds of recovery (Kessler et al., 2008), and poorer performance in decision-making tasks (Lorains et al., 2014) than do strategic gamblers. On the other hand, skill gamblers present a greater illusion of control than in chance gamblers, higher sensitivity to losses, and greater attention to wins (Lorains et al., 2014; Myrseth, Brunborg, & Eidem, 2010), and they tend to be more impulsive (Valleur et al., 2016). Furthermore, demographically and psychologically different profiles have been also described: Nonstrategic gamblers are more likely to be older females (Grant, Odlaug, Chamberlain, & Schreiber, 2012; Ledgerwood & Petry, 2006; Potenza et al., 2001) and to gamble as an attempt to escape from negative feelings such as depression or anxiety (Grant et al., 2012; Odlaug et al., 2011). In contrast, strategic gamblers are more likely to be younger males and to gamble to experience higher rates of action or arousal (Grant et al., 2012; Potenza et al., 2001). These findings suggest that the behavioral differences could be driven by distinct neurophysiological mechanisms. Despite the clinical implications that the presence of distinct types of gamblers might have, neuroimaging studies have systematically neglected this differentiation. In fact, it is unknown what oscillatory mechanisms might be responsible for the individual differences in gambling engagement between regular gamblers and nongamblers, and to what extent differential brain oscillatory mechanisms could also exist between skill and chance gamblers.
In this research, we aimed to override these limitations by studying oscillatory markers of reward processing in two groups of regular gamblers, with a preference for either skill or chance games, and one group of nongamblers while playing a slot machine task that has been widely used to study NM responses and the illusion of control (Chase & Clark, 2010; Clark et al., 2009; Sescousse et al., 2016). We focused especially on midfrontal theta and beta oscillations, two brain oscillatory responses that have been previously involved in reward processing and are related to functioning of the medial prefrontal cortex and ventral striatum, respectively (Cohen, Ridderinkhof, Haupt, Elger, & Fell, 2008; Luu, Tucker, & Makeig, 2004; Mas-Herrero, Ripollés, HajiHosseini, Rodríguez-Fornells, & Marco-Pallarés, 2015).
Theta oscillations have been suggested to reflect the motivational salience of behaviorally relevant outcomes (Andreou et al., 2017; Cavanagh, Frank, Klein, & Allen, 2010; Mas-Herrero & Marco-Pallarés, 2014, 2016). In gambling scenarios, although theta waves are chiefly related to negative feedback (Cavanagh et al., 2010; Cohen, Elger, & Ranganath, 2007; Marco-Pallarés et al., 2008), greater increases in midfrontal theta activity have also been observed following gains and NMs than following full misses (Alicart et al., 2015; Andreou et al., 2017; Doñamayor, Marco-Pallarés, Heldmann, Schoenfeld, & Münte, 2011; HajiHosseini, Rodríguez-Fornells, & Marco-Pallarés, 2012; & Marco-Pallarés, 2014).
On the other hand, increases of beta-frequency-band power have been described following positive outcomes (Alicart et al., 2015; Cohen et al., 2007; Doñamayor et al., 2011; HajiHosseini et al., 2012; Marco-Pallarés et al., 2008; Mas-Herrero et al., 2015) and NM events (Alicart et al., 2015), as compared to negative outcomes. In addition, this gain signal correlates with the engagement of reward-related structures, and it has been suggested to support orchestration of the different structures of reward networks (Andreou et al., 2017; Marco-Pallarés, Münte, & Rodríguez-Fornells, 2015; Mas-Herrero et al., 2015).
The main goal of the present study was to determine whether regular, nonpathological gamblers present differences in the neural oscillatory responses associated with feedback processing. Additionally, we aimed to assess whether gambling preference (chance or skill games) would reveal behavioral or neural differences between the groups of regular gamblers.
Method
Participants
A total of 54 healthy volunteers participated in the experiment. Participants were selected from a larger group of 1,744 people on the basis of their scores in a self-reported questionnaire consisting of a reduced version of the South Oaks Gambling Screen (SOGS; Lesieur & Blume, 1987). We adapted the questionnaire and the scoring so as not to get a pathological measure, but instead estimates of the regularity and amount of gambling. Items related to the assiduity of different types of gambling activities and five questions about gambling habits were kept from the original test, including “When you gamble, how often do you go back another day to win back the money you lost?” (answers: Never; less than half the time I lost; most of the time I lost; every time I lost); “Do you feel you have ever had a problem with gambling?” (answers: no; yes, in the past, but not now; yes); and three yes/no questions: “Did you ever gamble more than you intended?,” “Have people criticized your gambling?,” and “Have you ever lost time from work (or school) due to gambling?” Participants were instructed to answer how frequently they engaged in different types of gambling: Never, occasionally, once a month or more, or once a week or more. These responses were given, respectively, zero, one, two, or three points. For the questions, positive responses were given two points. The scores for the initial selection of potential participants were computed by summing up the overall points from the answers. The overall scores are represented in Fig. 1.
Histogram showing the distribution of the gambling test scores for men (N = 740, mean ± SD = 8.3 ± 6.4) and women (N = 1,004, mean ± SD = 4.3 ± 3.7). Light gray rectangles indicate the range of scores from which the participants were selected. Nongamblers (NG) had a score of zero or one point in the gambling test, and regular gamblers (RG) had a score equal to or greater than 14 points (9.73% of the 1,744 tests we passed satisfied this condition). People who gave a positive answer to the question about having a current gambling problem were not selected as participants.
People with very low and very high tendencies to gamble were selected to form the three different groups of the study. The group of nongamblers (NG; N = 20: 17 men, three women, 20.95 ± 3.6 years old) had scores of zero or one point on the questionnaire. The participants in the NG group were matched for gender and age with the two groups of regular gamblers. The regular gamblers were categorized as strategic or nonstrategic gamblers, depending on their most preferred games: skill games (skill gamblers, SkG; N = 18: 17 men, one woman, 22.17 ± 2.8 years old) or chance games (chance gamblers, ChG; N = 16: 13 men, three women, 23 ± 4.4 years old). There were no group differences in the age [F(2, 53) = 1.47, p = .241] or gender [χ2(2) < .001, p = .10] of the participants. The classification of regular gamblers as either SkG or ChG was done on the basis of their answers about gambling activities, assigning nine points if an answer was Once a week or more, four points if an answer was Once a month or more, and one point if the answer was Occasionally. The score for chance games was the sum for bingo, slot machines, and lotteries, whereas skill game preference was computed by adding up the points for games of skill (such as darts, pool, or bowling), cards (mostly poker), and sports betting. Regular gamblers were assigned to the group for which they presented the highest score. All the participants selected as regular gamblers presented scores between 14 and 26 points, with mean ± SD = 18.61 ± 2.7, and no differences were present between the overall scores for SkG and ChG [t(32) = 0.75, p = .46]. This global score for each member of the gamblers’ groups included at least one answer of gambling once a week or more, or more than one answer of gambling once a month or more. None of the participants had a diagnosis of problem gambling or were seeking treatment, had they been treated for problem gambling, were taking medication for any psychiatric or neurological problem, or had any psychiatric or neurological diagnosis.
Experimental design
The procedures of the experiment were approved by the Biomedical Research Institute of Bellvitge ethics committee, and informed consent in accordance with Declaration of Helsinki (1991, p. 1194) was obtained from all participants. Participants received a monetary reward at the end of the task, with one fixed part and a variable part that depended on their performance (proportional to their final number of points).
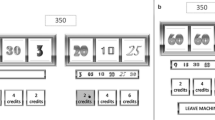
We used a modification of the slot machine task used in a previous experiment (Alicart et al., 2015; Fig. 2), presented with the Presentation software (Neurobehavioral Systems, Inc., Albany, CA). Participants had 5,000 points at the beginning of the task, and they could bet 10 or 25 points in each trial. These points were added or subtracted to the total points, depending on the result of each game: In the case of two nonmatching figures, participants lost the money bet. In case of winning (two of the same figure), they received four times the money bet. Finally, for noninformation trials, points were neither added nor subtracted. In half of the trials, participants could choose the image in the first reel they wanted to play (unforced selection condition, to generate the illusion of control). This was indicated by a blue arrow during the bet selection phase. In the other half of trials, the computer randomly selected the image from the first reel (two to six random movements before stopping), which was indicated by a red arrow (forced selection condition). The task consisted of 350 trials, with a 7-s break every 14 trials and a self-paced break every 70 trials. The outcomes were presented in a pseudorandom ratio, to ensure the proportion of each outcome (win: p = 1/7, N = 50; near-miss [NM]: p = 2/7, N = 100; full-miss or loss: p = 3/7, N = 150; and noninformation: p = 1/7, N = 50, designed as a control condition with the same percentage of wins, in order to discard probability effects on potential differences in brain responses to the different outcomes). The proportion of wins in our task was consistent with wins delivery in real slot machines, and the percentage of NMs was in accordance with previous studies assessing the optimal proportion of NMs to find their effect (Kassinove & Schare, 2001). NMs are loss outcomes in which the winning picture stops one step before (N = 50) or after (N = 50) the central position, so it could generate the expectation of winning.
Experimental design showing the steps for each trial. (1) In the first part of each trial, the participants could select to bet 10 or 25 points. (2) In half of the trials (N = 175), participants chose the image they wanted to play with, and in the other half of the trials, the image was selected by the computer. (3) After the image selection, the second reel spun for 2.5–3.5 s. (4) The second reel made a random number of 1-s movements (2, 3, or 4) before stopping. (5) The final outcome (win, loss, near-miss, or noninformation) was presented for 1 s.
We also included three questions after the different outcomes, the same questions used by Clark et al. (2009). The three questions were presented four times during the task for each different outcome: “How pleased are you with the last result?,” “How much do you want to continue to play the game?” and "How do you rate your chances of winning the next game?". The first two questions were presented just after the outcome, and the third question was presented after choosing the bet for the following trial. Participants provided subjective ratings using a 5-point scale, with the possible answers for the first question being 1. Very dissatisfied, 2. Dissatisfied, 3. Indifferent, 4. Satisfied, and 5. Very satisfied. Possible answers for the second and third questions were 1. Very little, 2. Little, 3. Indifferent, 4. Some, 5. Very much.
Electrophysiological recording
Electroencephalography (EEG) recordings were carried out using a BrainAmp amplifier (Brain Products GmbH; band-pass filter: 0.01–125 Hz, with a notch filter at 50-Hz and 250-Hz sampling rate) and an elastic cap with 29 electrode standard positions (Fp1/2, Fz, F7/8, F3/4, FCz, FC1/2, Fc5/6, Cz, C3/4, T7/8, Cp1/2, Cp5/6, Pz, P3/4, P7/8, Po1/2, and Oz), including the ground electrode. We also placed electrodes on the left and right mastoids, one electrode on the lateral outer canthus of the right eye to use as an online reference, and one electrode on the infraorbital ridge of the right eye to monitor eye movements. The electrode impedances were kept below 5 KΩ. Participants used the left and right mouse buttons to select their responses and the keyboard spacebar for the long breaks. They were also instructed to refrain from blinking.
Behavioral statistical analysis
All statistical tests were performed using the IBM SPSS 23.0 statistics software (IBM Corp., 2015). For the behavioral measures, we analyzed the selected bets, the latency from the previous result to the following bet selection, and the number of image changes before choosing the image to play (for the manual condition). Bet selection was a categorical variable with two possible values: high or low. For this reason, statistical analysis of the percentage of risky (high) bets selected among groups was performed by a generalized estimating equations model with a binomial probability function and a logit link function. We tested different covariance pattern models (independent and autoregressive), and the independent covariance pattern was the model with the highest goodness of fit. Significances are reported using the χ2 statistic (Wald test). Our bet analysis was carried out with the factors group, condition, and selection type (3 × 4 × 2: NG, SkG, or ChG; win, loss, NM, or noninformation; and player or computer selection, respectively).
Latency analyses were performed by calculating the time (in seconds) between the last outcome and the next bet selection and were entered into an analysis of variance (ANOVA) with the factors group and condition. One SkG participant with outlying latencies (> 3 SDs) was excluded from this analysis. The analysis of the image selection was performed by calculating the number of image changes before the final selection for the overall trials and then assessed with a Kruskal–Wallis H test for nonparametric data and Mann–Whitney’s U test for subsequent pairwise comparisons.
The analysis of the answers to the three questions (5-point Likert scale) was made by calculating the median for the answers, depending on the previous outcome (win, NM, loss, and noninformation) for each group, and performing a Kruskal–Wallis H test for nonparametric data and Mann–Whitney’s U test for subsequent pairwise comparisons.
Finally, all the variables that showed a main effect of group were included in a cross-validated discriminant analysis with the “leave-one-out” classification method, to assess their ability to discriminate and classify individuals from the three groups on the basis of their behavioral and electrophysiological responses. The variables included in this analysis were bet selection depending on selection type, latencies to next bet selection, number of image changes, theta power increases for NMs and wins, and beta power increases for wins.
Multiple comparisons were corrected for all behavioral and EEG analyses involving the ANOVA and post-hoc pairwise and independent-sample t tests, by controlling the false discovery rate (FDR) according to the Benjamini and Hochberg procedure at a level of .05. Adjusted p values (q) are reported for these analyses.
EEG analysis
The EEG recordings were analyzed using the EEGLAB toolbox (Delorme & Makeig, 2004). EEGs were re-referenced offline to the mean of the activity at the two mastoid electrodes, and then a time–frequency analysis was performed by using a continuous complex Morlet wavelet of seven cycles on the single-trial data for each participant, for epochs comprising 4,000 ms (2,000 ms before to 2,000 ms after the outcome) in the frequencies from 1 to 40 Hz. Within this time window, trials were baseline corrected, with a baseline defined from 100 ms prior to the outcome onset (– 100 to 0 ms).
Trials with amplitudes higher than 100 μV in the EEG or electrooculography (from – 100 ms to 1 s after stimuli) were rejected from further analysis. Changes in time-varying energy were computed by squaring the convolution between wavelet and signal for each trial and participant, depending on the different conditions. Separate ANOVAs were conducted for the mean increase/decrease in power for low theta (4–6 Hz) and beta (15–20 Hz) frequencies, with the factors group (NG, SkG, and ChG), condition (win, NM, and loss), and selection type (automatic and manual).
The Greenhouse–Geisser epsilon was used to correct for violations of the sphericity assumption for all statistical effects involving two or more degrees of freedom in the numerator. Two participants from the NG group with outlying theta values (> 3 SDs of the group) were removed from the theta analyses for the win and NM conditions.
Results
Behavioral results
We first analyzed the betting patterns of the different groups. The generalized estimating equations model was calculated for the percentage of risky bets depending on the previous outcome and selection type [group (NG, SkG, and ChG); condition (win, NM, loss, and noninformation); and type (manual or automatic selection)], revealing significant effects of selection type [χ2(1) = 37.96, p = 7.21·10–7], condition [χ2(3) = 15.56, p = .001], and group [χ2(2) = 9.57, p = .008], and a significant interaction between selection type and group [χ2(2) = 8.39, p = .015; Figs. 3A and 3B]. Regarding group differences, regular gamblers chose a significantly greater number of risky bets than did NG (SkG, p = .002, q = .006; ChG, p = .044, marginal at FDR, q = .066). No differences were found between regular gamblers (p = .78). Intragroup pairwise comparisons for selection type showed a larger number of risky bets selected in the manual than in the automatic condition for the three groups (NG, p = .003; ChG, p = .012; and SkG, p = 2.35·10–7; q < .012), indicating that manual trials generated an illusion of control. Post-hoc pairwise comparisons for the interaction between group and selection revealed a larger number of risky bets for manual selection for SkG (p = .00003, q = .0002) and ChG (uncorrected p = .049, q = .18) in comparison with NG. For the automatic condition, marginally significant differences were found between ChG and NG (p = .06, q = .12).
(a) Group proportions of risky bets chosen, depending on the previous result. (b) Overall risky bets, depending on selection type. (c) Behavioral results for image selection. (d) Latencies between the previous outcome and the next bet selection. NG, nongamblers; SkG, skill gamblers; ChG, chance gamblers; NM, near-miss; NI, noninformation. *, significant at the p < .05 level; +, marginally significant. The error bars in C and D indicate standard errors of the means.
The Kruskal–Wallis H test for independent samples on the overall number of image changes before image selection (Fig. 3C) showed significant group differences [χ2(2) = 14.9, p = .001]. A Mann–Whitney U test revealed differences in the number of image changes between NG and both groups of regular gamblers, with larger numbers for both SkG (U = 50, Z = 3.80, p = .00006, q = .0002) and ChG (U = 79, Z = 2.58, p = .009, q = .013) than for NG. No difference was found between the two groups of regular gamblers (U = 126, Z = 0.6, p = .55).
We also analyzed the time (in seconds) that participants spent after each outcome before choosing the next bet. The ANOVA with condition and group as factors revealed a significant difference among the conditions [F(3, 150) = 5.2, p = .007] and a group effect [F(2, 50) = 8.41, p = .001]. We found no significant interaction between the factors. Overall, participants placed their bids faster following noninformation trials than following the other conditions. Figure 3D shows the overall latencies for the NG, SkG, and ChG. An independent-sample t test among groups for overall latencies revealed shorter latencies for SkG than for either NG [t(35) = 4.75, p = .00006, q = .0002] or ChG [t(31) = 2.32, p = .03, q = .045], and marginally significant shorter latencies for ChG than for NG [t(34) = 1.99, p = .05, q = 054].
Possible differences between the answers to the three questions (“How pleased are you with the last result?,” “How much do you want to continue to play the game?,” and “How do you rate your chances of winning the next game?”) were assessed by entering the median values for each question and condition into a Kruskal–Wallis H test for independent samples. No group differences were found for any of the questions. This result might have been due to the small number of question presentations included during the experiment.
Time–frequency
Time–frequency analyses were performed for the low theta (4–6 Hz) and low beta (15–20 Hz) frequency bands. Figure 4 shows time–frequency plots for the three groups in the win, NM, and loss conditions. A repeated measures ANOVA for theta power increases was performed in the time window from 300 to 500 ms after the outcome. Given the topographies of the different effects (see Figs. 4 and 5), we included a factor for electrode location (central electrodes Fz, Cz, and Pz), together with the factors group, selection type, and condition. Repeated measures ANOVAs revealed significant effects of condition [F(2, 98) = 58.07, p = 1.6896·10–16], selection type [F(1, 49) = 22.76, p = .00002], and electrode [F(2, 98) = 13.66, p = .00006]. Across groups, only the Condition × Electrode × Group interaction was significant [F(8, 196) = 2.25, p = .025]. Separate ANOVAs for the Fz, Cz, and Pz electrodes with the factors condition, group, and selection type revealed a significant interaction between condition and group only for the Cz electrode [F(4, 98) = 3.25, p = .02; F(4, 98) = 2.35, p = .07, for Fz; and F(4, 98) = 1.26, p = .29, for Pz]. Therefore, we analyzed the power values at this electrode. The ANOVA results also showed significant differences among conditions [F(2, 98) = 47.91, p = 9.54·10–14] and selection types [F(1, 49) = 20.26, p = .00004], a significant interaction between condition and group [F(4,98)=3.25, p=.020], as well as a marginally significant group effect [F(2, 49) = 2.97, p = .06]. There were no significant differences in the interaction between group and selection type or condition and selection type, nor in the interaction among the three factors (Fig. 5).
Topographical maps and time–frequency plots of power distribution in the theta frequency band (4–6 Hz, 300- to 500-ms window) at electrode Cz from 100 ms before the outcome (baseline) to 1,000 ms after, for the win (a), near-miss (NM; b), and loss (c) outcomes in nongamblers (NG, left), skill gamblers (SkG, center), and chance gamblers (ChG, right).
(a) Topographical maps of power distribution in the theta frequency band (4–6 Hz, 300- to 500-ms window) for NG, SkG, and ChG in the overall win, NM, and loss conditions. Time–frequency plots of spectral power differences are shown at electrode Cz from 100 ms before the outcome (baseline) to 1,000 ms after the outcome for ChG-over-NG differences in the win, NM, and loss conditions. (b) Power increases for the overall win, NM, and loss conditions among NG, SkG, and ChG. NM, near-miss; NG, nongamblers; SkG, skill gamblers; ChG, chance gamblers; *, significant at the p < .05 level; +, marginally significant.
The outcomes from manually selected images elicited larger theta power increases than did automatic selection [t(51) = 4.32, p = .00003]. Post-hoc independent-sample t tests for overall win, NM, and loss outcomes revealed a larger theta increase in wins for ChG than for NG [t(32) = 2.50, p = .018, q = .05], and a marginally larger one for ChG than for SkG [t(32) = 1.87, p = .07, q = 0.1]. No significant differences were found between SkG and NG [t(34) = 0.42, p = .68]. Regarding NM outcomes for the theta frequency band, both groups of gamblers presented larger power increases compared with NG [t(34) = 2.68, p = .011, q = .03, for SkG vs. NG; and t(32) = 2.16, p = .039, for ChG vs. NG, marginal after FDR correction q = .058]. No significant differences were found between the two groups of regular gamblers [t(32) = 0.05, p = .96]. Finally, group comparisons for loss outcomes revealed no significant differences. Regarding the differences among conditions for the different groups (interaction effect), NG and ChG showed larger theta oscillatory activity after wins and NMs than after losses [for NG, t(17) = 3.24, p = .005, q = .01, and t(17) = 4.11, p = .001, q = .002, respectively; for ChG, t(15) = 5.69, p = .00004, q = .0004, and t(15) = 5.56, p = .00005, q = .0002, respectively]. No differences were present between win and NM outcomes [for NG, t(17) = 1.42, p = .18; for ChG, t(15) = 0.99, p = .34, respectively]. In contrast, SkG presented differences among the three conditions, with larger increases for NMs than for wins and losses [t(17) = 4.54, p = .0003, q = .001, and t(17) = 6.70, p = .000004, q = .0002], as well as larger increases for win than for loss outcomes [t(17) = 2.34, p = .03, q = .04].
The time–frequency analysis for beta frequency (15–20 Hz) was performed in the time window from 150 to 350 ms after the outcome. Given the topography of the effect (Fig. 6), beta-band analyses were carried out by using the mean values for the Fz, FCz, F4, and FC2 electrodes. A repeated measures ANOVA with the factors group, condition, and selection type revealed significant differences among the conditions [F(2, 102) = 14.34, p = .00001] and an interaction between group and condition [F(4, 102) = 3.39, p = .018]. No differences were found for selection type [F(1, 51) = 2.16, p = .15], for the interaction between selection type and group [F(2, 51) = 0.65, p = .53], or for the interaction among the three factors [F(4, 102) = 0.47, p = .76]. Wins and NMs elicited larger beta power increases than did losses [t(53) = 4.12, p = .00014, and t(53) = 4.86, p = .00001, respectively]. No differences were found between win and NM outcomes [t(53) = 1.16, p = .25]. Post-hoc independent-sample t tests for win outcomes showed larger power increases for SkG and ChG than for NG [t(36) = 2.78, p = .009, q = .03, and t(34) = 2.18, p = .036, q = .05, respectively; Fig. 6]. Win responses were not statistically different between regular gamblers [t(32) = 0.74, p = .47], and beta power increases to NM and loss outcomes did not present differences among the groups.
(a) Topographical maps of power distribution in the beta frequency band (15–20 Hz, 150- to 350-ms window) for NG, SkG, and ChG in the overall win condition. The time–frequency plot shows spectral power differences at electrode FCz from 100 ms before the outcome (baseline) to 1,000 ms after the outcome for ChG-over-NG differences for win outcomes. (b) Power increases for NG, SkG, and ChG for overall wins. NM, near-miss; NG, nongamblers; SkG, skill gamblers; ChG, chance gamblers; *, significant at the p < .05 level.
The results from the cross-validated discriminant analysis, with the variables bet selection depending on selection type, latencies to next bet selection, number of image changes, theta power increases for NMs and wins, and beta power increases for wins revealed two discriminant functions. The first function explained 76.6% of the variance, canonical R2 = .53, and the second explained 23.4%, canonical R2 = .26. Jointly, these discriminant functions significantly differentiated the groups of participants, Ʌ = .35, χ2(14) = 48.1, p = .00001. The second function alone also significantly differentiated the groups, Ʌ = .75, χ2(6) = 13.56, p = .035. The discriminant function plot showed that the first function discriminated NG more strongly from regular gamblers, and the second function differentiated ChG from the other two groups. The correlations between outcomes and the discriminant functions revealed that numbers of image changes, risky bet selection for manual trials, latencies, beta power for wins, and theta power for NMs loaded more highly on the first function (rs = .56, .53, – .51, .38, and .32, respectively) than on the second (rs = – .02, – .10, .10, .01, and .20, respectively). On the other hand, theta power increases for win outcomes and risky bet selection for automatic trials loaded more highly on the second function (rs = .61 and .36) than on the first (rs = .12 and .23, respectively). Overall, the analysis revealed that 73.1% of the original group cases and 61.5% of the cross-validated grouped cases were correctly classified.
Discussion
The goal of this study was to assess the brain oscillatory correlates of gambling outcomes processing in regular gamblers, depending on their preferred gambling modality. The main results from the analyses of behavioral and oscillatory responses indicated that specific differences exist among groups, not only between NG and regular gamblers, but also between groups of gamblers depending on the types of activities they engage in. Most of the previous studies with gamblers were performed in clinical populations. The novelty of the present investigation was in both the study of electrophysiological brain responses to gambling outcomes, with special attention to the invigorating effect of near-misses, in nonpathological regular gamblers, and the differentiation by gambling types.
First, our behavioral results indicate that regular gamblers, as compared to NG, were more likely to select risky bets, were faster making this decision, and selected more carefully the image to play with, despite it having no consequences for the outcome obtained. In this regard, previous studies have reported a preference for riskier and disadvantageous choices and a higher illusion of control in pathological gambling, which in turn leads to worse performance in decision-making and gambling tasks (Goodie, 2005; Myrseth et al., 2010; Oberg, Christie, & Tata, 2011; Orgaz, Estévez, & Matute, 2013). Interestingly, some differences were also found between SkG and ChG. SkG showed a larger number of risky bets for the manual selection than did NG, but not during the automatic selection. In contrast, ChG tended to differ from NG for both automatic and manual selections. These differences might indicate that SkG are susceptible to developing a greater illusion of control when instrumental control is present, but not in its absence. These differences among groups reveal different strategies based on chance or skill, although all groups were playing a chance game. Similar slot-machine-like tasks have been used in previous research (Chase & Clark, 2010; Clark et al., 2009; Sescousse et al., 2016) in both healthy participants and pathological gamblers independent of their gambling preference. Moreover, we were particularly interested in studying neural responses to NMs, which can be easily configured with this kind of task. Another important point to remark is that our participants from the chance group were not all slot machine players, and although the two groups were chosen on the basis of their most preferred type of game, most participants played a variety of games, including strategic and nonstrategic ones. It would be of great interest to replicate the present results in a future study with chance and skill gamblers playing a strategic game (e.g., poker or blackjack).
We also found differences among the groups at the neural level. Specifically, regular gamblers showed greater theta and beta power increases than did NG following NMs and wins, respectively. NM outcomes elicited increased theta responses, as compared with full misses (also shown in Alicart et al., 2015; Dymond et al., 2014), with larger increases in both groups of regular gamblers than in NG. It is well known that NM outcomes invigorate gambling in the general population (Côté et al., 2003; Griffiths, 1991). Previous studies using intracranial recording and source modeling have suggested that theta oscillations are generated in the medial prefrontal cortex (Cohen et al., 2008; Luu et al., 2004; Mas-Herrero & Marco-Pallarés, 2016) and are thought to coordinate motivational and attentional networks in reward processing in response to behaviorally relevant outcomes (Cavanagh et al., 2010; Mas-Herrero & Marco-Pallarés, 2014, 2016). Thus, differences in theta oscillations following NMs may reflect a stronger influence of NMs in regular gamblers than in NG. In agreement with our findings, Dymond et al. (2014), in an fMRI and magnetoencephalographic study, found out a correlation between theta power increases in response to NMs and SOGS scores, a measure of gambling severity (Lesieur & Blume, 1987). In addition, theta activity after NMs was localized in areas of the salience network (orbitofrontal cortex and insula) functionally connected with the medial prefrontal cortex. Interestingly, Sescousse et al. (2016) found increased response in ventral striatum to NMs in problem gamblers as compared with healthy controls, and Chase and Clark (2010) found that activation of the ventral striatum after NM outcomes was predictive of gambling severity in a group of pathological gamblers. Together, these results indicate that NMs have a stronger motivational impact on gamblers than on people who do not engage in gambling.
Notably, ChG, but not SkG, presented greater increases in theta oscillatory activity following wins than did NG. According to the discriminant analysis, theta power increases following wins and risky bets during automatic selection allowed us to discriminate between ChG and the other two groups. This result supports the existence of different subtypes of gamblers, which may be reflected in part in their preference for either chance or skill games. Further studies will be required in order to explore the extent to which these differences between gamblers rely on greater sensitivity to an illusion of control, learning deficits, or motivational aspects, among other factors.
In addition to the theta-frequency-band results, the present study has been, to our knowledge, the first to report an increase of beta oscillatory activity to win outcomes in regular gamblers in comparison with NG. Previous studies have consistently showed beta power increases following rewarding outcomes (Cohen et al., 2007; Doñamayor et al., 2011; Marco-Pallarés et al., 2008; Mas-Herrero et al., 2015). Importantly, we also replicated a result of our previous study (Alicart et al., 2015), showing similar beta oscillatory activity after NM and win outcomes, both larger than the activity after standard losses. Beta oscillatory activity has been proposed as a key mechanism for the coupling between the prefrontal and striatal structures underlying the neural signaling of unexpected and relevant positive outcomes (Marco-Pallarés et al., 2015). Previous studies combining EEG and fMRI have shown that cortical beta oscillations may reflect the engagement of reward and memory structures such as the striatum and the hippocampus (Andreou et al., 2017; Mas-Herrero et al., 2015) and that differences in dopaminergic transmission modulate this signal (Marco-Pallarés et al., 2009). Thus, differences in beta oscillatory activity between regular gamblers and NG in response to wins would be in line with previous results suggesting overactivation of reward-related structures in response to wins for pathological gamblers (Hewig et al., 2010; Oberg et al., 2011). This result contrasts with the lack of group differences in beta responses to NMs, a difference driven by theta response.
The present findings add evidence that game preferences entail different brain responses to gambling outcomes between skill and chance regular gamblers. Behavioral results showed differences between groups according to the gambling preference, and the win condition presented differences between regular gamblers in theta oscillatory activity. Despite the differences, a common pattern of responses between regular gamblers and NG regarding theta and beta oscillatory activity should be highlighted. As we mentioned above, larger theta responses to NM outcomes have been consistently related to pathological gambling (Chase & Clark, 2010; Dymond et al., 2014; Habib & Dixon, 2010). However, an open question from the present study is to what extent the present results could be applied to the study of pathological gambling. Indeed, the two groups of gamblers presented a high frequency of gambling behaviors, as reflected by their high scores in the gambling test, but the lack of clinical measures such as depressive symptom intensity, anxiety, or impulsiveness in the present study do not allow for determining the risk of further development of gambling disorder. Therefore, although the present results show that heightened theta responsiveness to NMs is a robust feature in regular gambling and could constitute a vulnerability marker for pathological gambling, further longitudinal studies will be necessary to confirm this hypothesis and establish a relationship between the altered neural responses found in regular gamblers and eventual progression to a gambling disorder.
Author note
This work was supported by grants from the Spanish Government [PSI2012-37472, PSI2015-69664-P] to J.M.-P. H.A. was supported by a grant from the Spanish Government [BES-2013-067440]. E.M.-H. was supported by a CIBC Fellowship in Brain Imaging from the Montreal Neurological Institute. The funding sources were not involved in the study design; in the collection, analysis, and interpretation of the data; in the writing of the report; nor and in the decision to submit the article for publication. The authors declare no competing financial interests.
References
Alicart, H., Cucurell, D., Mas-Herrero, E., & Marco-Pallarés, J. (2015). Human oscillatory activity in near-miss events. Social Cognitive and Affective Neuroscience, 10, 1405–1412. doi:https://doi.org/10.1093/scan/nsv033
Andreou, C., Frielinghaus, H., Rauh, J., Mußmann, M., Vauth, S., Braun, P., . . . Mulert, C. (2017). Theta and high-beta networks for feedback processing: A simultaneous EEG–fMRI study in healthy male subjects. Translational Psychiatry, 7, e1016. doi:https://doi.org/10.1038/tp.2016.287
Binde, P. (2005). Gambling, exchange systems, and moralities. Journal of Gambling Studies, 21, 445–479. doi:https://doi.org/10.1007/s10899-005-5558-2
Breen, R. B., & Zimmerman, M. (2002). Rapid onset of pathological gambling in machine gamblers. Journal of Gambling Studies, 18, 31–43. https://doi.org/10.1023/A:1014580112648
Cavanagh, J. F., Frank, M. J., Klein, T. J., & Allen, J. J. B. (2010). Frontal theta links prediction errors to behavioral adaptation in reinforcement learning. NeuroImage, 49, 3198–3209. doi:https://doi.org/10.1016/j.neuroimage.2009.11.080
Chase, H. W., & Clark, L. (2010). Gambling severity predicts midbrain response to near-miss outcomes. Journal of Neuroscience, 30, 6180–6187. doi:https://doi.org/10.1523/JNEUROSCI.5758-09.2010
Clark, L., Lawrence, A. J., Astley-Jones, F., & Gray, N. (2009). Gambling near-misses enhance motivation to gamble and recruit win-related brain circuitry. Neuron, 61, 481–490. doi:https://doi.org/10.1016/j.neuron.2008.12.031
Clark, L., Crooks, B., Clarke, R., Aitken, M. R. F., & Dunn, B. D. (2012). Physiological responses to near-miss outcomes and personal control during simulated gambling. Journal of Gambling Studies, 28, 123–137. doi:https://doi.org/10.1007/s10899-011-9247-z
Cohen, M. X., Elger, C. E., & Ranganath, C. (2007). Reward expectation modulates feedback-related negativity and EEG spectra. NeuroImage, 35, 968–978. doi:https://doi.org/10.1016/j.neuroimage.2006.11.056
Cohen, M. X., Ridderinkhof, K. R., Haupt, S., Elger, C. E., & Fell, J. (2008). Medial frontal cortex and response conflict: evidence from human intracranial EEG and medial frontal cortex lesion. Brain Research, 1238, 127–142. doi:https://doi.org/10.1016/j.brainres.2008.07.114
Côté, D., Caron, A., Aubert, J., Desrochers, V., & Ladouceur, R. (2003). Near wins prolong gambling on a video lottery terminal. Journal of Gambling Studies, 19, 433–438.
Delorme, A., & Makeig, S. (2004). EEGLAB: An open source toolbox for analysis of single-trial EEG dynamics including independent component analysis. Journal of Neuroscience Methods, 134, 9–21. doi:https://doi.org/10.1016/j.jneumeth.2003.10.009
Doñamayor, N., Marco-Pallarés, J., Heldmann, M., Schoenfeld, M. A., & Münte, T. F. (2011). Temporal dynamics of reward processing revealed by magnetoencephalography. Human Brain Mapping, 32, 2228–2240. doi:https://doi.org/10.1002/hbm.21184
Dymond, S., Lawrence, N. S., Dunkley, B. T., Yuen, K. S. L., Hinton, E. C., Dixon, M. R., . . . Singh, K. D. (2014). Almost winning: Induced MEG theta power in insula and orbitofrontal cortex increases during gambling near-misses and is associated with BOLD signal and gambling severity. NeuroImage, 91, 210–219. doi:https://doi.org/10.1016/j.neuroimage.2014.01.019
Goodie, A. S. (2005). The role of perceived control and overconfidence in pathological gambling. Journal of Gambling Studies, 21, 481–502. doi:https://doi.org/10.1007/s10899-005-5559-1
Grant, J. E., Odlaug, B. L., Chamberlain, S. R., & Schreiber, L. R. N. (2012). Neurocognitive dysfunction in strategic and non-strategic gamblers. Progress in Neuro-Psychopharmacology & Biological Psychiatry, 38, 336–340. doi:https://doi.org/10.1016/j.pnpbp.2012.05.006
Griffiths, M. (1991). Interdisciplinary and applied psychobiology of the near-miss in fruit machine gambling. Journal of Psychology, 125, 347–57. doi:https://doi.org/10.1080/00223980.1991.10543298
Habib, R., & Dixon, M. R. (2010). Neurobehavioral evidence for the “Near-Miss” effect in pathological gamblers. Journal of the Experimental Analysis of Behavior, 93, 313–328. doi:https://doi.org/10.1901/jeab.2010.93-313
HajiHosseini, A., Rodríguez-Fornells, A., & Marco-Pallarés, J. (2012) The role of beta-gamma oscillations in unexpected rewards processing. NeuroImage, 60, 1678–1685. doi:https://doi.org/10.1016/j.neuroimage.2012.01.125
Hewig, J., Kretschmer, N., Trippe, R. H., Hecht, H., Coles, M. G. H., Holroyd, C. B., & Miltner, W. H. R. (2010). Hypersensitivity to reward in problem gamblers. Biological Psychiatry, 67, 781–783. doi:https://doi.org/10.1016/j.biopsych.2009.11.009
IBM Corp. (2015). IBM SPSS Statistics for Windows (Version 23.0). Armonk, NY: IBM Corp.
Kassinove, J. I., & Schare, M. L. (2001). Effects of the “near miss” and the “big win” on persistence at slot machine gambling. Psychology of Addictive Behaviors, 15, 155–158.
Kessler, R. C., Hwang, I., LaBrie, R., Petukhova, M., Sampson, N. A., Winters, K. C., & Shaffer, H. J. (2008). DSM-IV pathological gambling in the National Comorbidity Survey Replication. Psychological Medicine, 38, 1351–1360. doi:https://doi.org/10.1017/S0033291708002900
Langer, E. J. (1975). The illusion of control. Journal of Personality and Social Psychology, 32, 311–328. doi:https://doi.org/10.1037/0022-3514.32.2.311
Ledgerwood D. M., & Petry N. M. (2006). Psychological experience of gambling and subtypes of pathological gamblers. Psychiatry Research, 144, 17–27. doi:https://doi.org/10.1016/j.psychres.2005.08.017
Leotti, L. A., & Delgado, M. R. (2011). The inherent reward of choice. Psychological Science, 22, 1310–1318. doi:https://doi.org/10.1177/0956797611417005
Lesieur, H. R., & Blume, S. B. (1987). The South Oaks Gambling Screen (SOGS): A new instrument for the identification of pathological gamblers. American Journal of Psychiatry, 144, 1184–1188. doi:https://doi.org/10.1176/ajp.144.9.1184
Lorains, F. K., Dowling, N. A., Enticott, P. G., Bradshaw, J. L., Trueblood, J. S., & Stout, J. C. (2014). Strategic and non-strategic problem gamblers differ on decision-making under risk and ambiguity. Addiction, 109, 1128–1137. doi:https://doi.org/10.1111/add.12494
Lorenz, R. C., Gleich, T., Kühn, S., Pöhland, L., Pelz, P., Wüstenberg, T., . . . Beck, A. (2015). Subjective illusion of control modulates striatal reward anticipation in adolescence. NeuroImage, 117, 250–257. doi:https://doi.org/10.1016/j.neuroimage.2015.05.024
Luu, P., Tucker, D. M., & Makeig, S. (2004). Frontal midline theta and the error-related negativity: neurophysiological mechanisms of action regulation. Clinical Neurophysiology, 115, 1821–1835. doi:https://doi.org/10.1016/j.clinph.2004.03.031
Marco-Pallarés, J., Cucurell, D., Cunillera, T., García, R., Andrés-Pueyo, A., Münte, T. F., & Rodríguez-Fornells, A. (2008). Human oscillatory activity associated to reward processing in a gambling task. Neuropsychologia, 46, 241–248. doi:https://doi.org/10.1016/j.neuropsychologia.2007.07.016
Marco-Pallarés, J., Cucurell, D., Cunillera, T., Krämer, U. M., Càmara, E., Nager, W., . . . Rodríguez-Fornells, A. (2009). Genetic variability in the dopamine system (dopamine receptor D4, catechol-O-methyltransferase) modulates neurophysiological responses to gains and losses. Biological Psychiatry, 66, 154–161. doi:https://doi.org/10.1016/j.biopsych.2009.01.006
Marco-Pallarés, J., Münte, T. F., & Rodríguez-Fornells, A. (2015). The role of high-frequency oscillatory activity in reward processing and learning. Neuroscience & Biobehavioral Reviews, 49, 1–7. doi:https://doi.org/10.1016/j.neubiorev.2014.11.014
Mas-Herrero, E., & Marco-Pallarés, J. (2014). Frontal theta oscillatory activity is a common mechanism for the computation of unexpected outcomes and learning rate. Journal of Cognitive Neuroscience, 26, 447–458. doi:https://doi.org/10.1162/jocn_a_00516
Mas-Herrero, E., & Marco-Pallarés, J. (2016). Theta oscillations integrate functionally segregated sub-regions of the medial prefrontal cortex. NeuroImage, 143, 166–174. doi:https://doi.org/10.1016/j.neuroimage.2016.08.024
Mas-Herrero, E., Ripollés, P., HajiHosseini, A., Rodríguez-Fornells, A., & Marco-Pallarés, J. (2015). Beta oscillations and reward processing: Coupling oscillatory activity and hemodynamic responses. NeuroImage, 119, 13–19. doi:https://doi.org/10.1016/j.neuroimage.2015.05.095
Myrseth, H., Brunborg, G., & Eidem, M. (2010). Differences in cognitive distortions between pathological and non-pathological gamblers with preferences for chance or skill games. Journal of Gambling Studies, 26, 561–569. doi:https://doi.org/10.1007/s10899-010-9180-6
Oberg, S. A., Christie, G. J., & Tata, M. S. (2011). Problem gamblers exhibit reward hypersensitivity in medial frontal cortex during gambling. Neuropsychologia, 49, 3768–3775. doi:https://doi.org/10.1016/j.neuropsychologia.2011.09.037
Odlaug, B. L., Marsh, P. J., Kim, S. W., & Grant, J. E. (2011). Strategic vs. nonstrategic gambling: Characteristics of pathological gamblers based on gambling preference. Annals of Clinical Psychiatry, 23, 105–112.
Orgaz, C., Estévez, A., & Matute, H. (2013). Pathological gamblers are more vulnerable to the illusion of control in a standard associative learning task. Frontiers in Psychology, 4, 306. doi:https://doi.org/10.3389/fpsyg.2013.00306
Petry, N. M., Stinson, F. S., & Grant, B. F. (2005). Comorbidity of DSM-IV pathological gambling and other psychiatric disorders: Results from the National Epidemiologic Survey on Alcohol and Related Conditions. Journal of Clinical Psychiatry, 66, 564–574.
Potenza, M. N., Steinberg, M. A., McLaughlin, S. D., Wu, R., Rounsaville, B. J., & O’Malley, S. S. (2001). Gender-related differences in the characteristics of problem gamblers using a gambling helpline. American Journal of Psychiatry, 158, 1500–1505. https://doi.org/10.1176/appi.ajp.158.9.1500
Sescousse, G., Janssen, L. K., Hashemi, M. M., Timmer, M. H. M., Geurts, D. E. M., ter Huurne, N. P., . . . Cools, R. (2016). Amplified striatal responses to near-miss outcomes in pathological gamblers. Neuropsychopharmacology, 41, 2614–2623. doi:https://doi.org/10.1038/npp.2016.43
Shen, Y., Kairouz, S., Nadeau, L., & Robillard, C. (2015). Comparing problem gamblers with moderate-risk gamblers in a sample of university students. Journal of Behavioral Addictions, 4, 53–59. doi:https://doi.org/10.1556/2006.4.2015.002
Ulrich, N., & Hewig, J. (2014). A miss is as good as a mile? Processing of near and full outcomes in a gambling paradigm. Psychophysiology, 51, 819–823. https://doi.org/10.1111/psyp.12232
Valleur, M., Codina, I., Vénisse, J.-L., Romo, L., Magalon, D., Fatséas, M., . . . Challet-Bouju, G. (2016). Towards a validation of the three pathways model of pathological gambling. Journal of Gambling Studies, 32, 757–771. doi:https://doi.org/10.1007/s10899-015-9545-y
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Alicart, H., Mas-Herrero, E., Rifà-Ros, X. et al. Brain oscillatory activity of skill and chance gamblers during a slot machine game. Cogn Affect Behav Neurosci 19, 1509–1520 (2019). https://doi.org/10.3758/s13415-019-00715-1
Published:
Issue Date:
DOI: https://doi.org/10.3758/s13415-019-00715-1