Abstract
In daily life, humans often perform visual tasks, such as solving puzzles or searching for a friend in a crowd. Performing these visual searches jointly with a partner can be beneficial: The two task partners can devise effective division of labor strategies and thereby outperform individuals who search alone. To date, it is unknown whether these group benefits scale up to triads or whether the cost of coordinating with others offsets any potential benefit for group sizes above two. To address this question, we compare participants’ performance in a visual search task that they perform either alone, in dyads, or in triads. When the search task is performed jointly, co-actors receive information about each other’s gaze location. After controlling for speed–accuracy trade-offs, we found that triads searched faster than dyads, suggesting that group benefits do scale up to triads. Moreover, we found that the triads’ divided the search space in accordance with the co-actors’ individual search performances but searched less efficiently than dyads. We also present a linear model to predict group benefits, which accounts for 70% of the variance. The model includes our experimental factors and a set of non-redundant predictors, quantifying the similarities in the individual performances, the collaboration between co-actors, and the estimated benefits that co-actors would attain without collaborating. Overall, the present study demonstrates that group benefits scale up to larger group sizes, but the additional gains are attenuated by the increased costs associated with devising effective division of labor strategies.
Similar content being viewed by others
Introduction
Humans frequently perform tasks collaboratively (Frith & Frith, 2012; Vesper et al., 2017; Sebanz et al., 2006). These tasks are often visual in nature and are performed while people reside in the same physical location—for instance, when jointly looking at maps, looking for a friend in a crowd, or jointly solving puzzles. Alternatively, humans may also reside in remote locations while performing visual tasks together—for instance, when jointly playing computer games online or working on research reports in shared online documents. In such situations, co-actors may distribute task demands to reach a higher performance compared to when performing the same task alone (i.e., there is a “group benefit”). For instance, when searching for a friend in a crowd, one person may search the left half of the crowd while the other searches the right half (Brennan et al., 2008).
Research on group benefits in joint visual tasks has investigated a number of factors that influence if, and to what extent, groups can outperform individuals (Bahrami et al., 2010; Brennan et al., 2008; Brennan & Enns 2015a, 2015b; Szymanski et al., 2017; Wahn et al., 2017, 2018a, 2018c). A prominent factor is the availability of information about the co-actors’ actions (Brennan et al., 2008; Neider et al., 2010; Wahn et al., 2016c, 2017). For instance, in a joint visual search task (Brennan et al., 2008), pairs of participants were instructed to search for a target among distractor stimuli on a computer screen, and one of the manipulated factors was the availability of gaze information. Specifically, each co-actor received information as to where their partner was looking via a cursor that was displayed on the computer screen. Brennan et al., (2008) found that pairs who received gaze information outperformed participants searching alone by using the information about the co-actor’s actions to effectively distribute the labor in the visual search task. For instance, one co-actor may search the left part of the screen while the other co-actor may search the right part of the screen. In sum, these findings suggest that the availability of information about each other’s actions (henceforth, referred to as “receiving action information”) is an important factor that enables pairs to attain a group benefit.
As a point of note, in the experimental design by Brennan et al., (2008) participants were in different rooms and they could not see each other. Gaze information of the co-actor was delivered via a cursor displayed on one’s computer screen. Thus, it might be argued that this situation does not resemble any real-world scenarios where people search together. While such a point might have been valid in 2008, in present times people frequently perform tasks collaboratively online in remote locations and receive abstracted online information about a co-actors’ actions (e.g., a moving mouse cursor). Thus, experimental designs as used by Brennan et al., (2008) are becoming increasingly more relevant to present day collaborative tasks.
While group benefits have been demonstrated for dyads (Brennan et al., 2008), it is unknown whether comparable results apply to group sizes larger than two. Does the availability of information about each other’s actions lead to benefits in performance for triads over and above the benefits for dyads? As stated above, in the earlier study by Brennan et al., (2008), co-actors used the gaze information to effectively distribute the labor. Co-actors in triads may similarly use such information about each other’s actions to devise effective division of labor strategies to outperform dyads and attain a group benefit. Alternatively, they could be overwhelmed by the demands to effectively coordinate with two co-actors and fail to attain a group benefit. That is, each member of a triad would need to keep track of the search locations of two co-actors compared to tracking the search location of only one co-actor as in Brennan et al., (2008). Relatedly, research on an object tracking task—a task where participants track the movements of multiple objects among distractors—has quantified how increases in the number of tracked targets lead to a higher attentional load (Alnæs et al., 2014; Sternshein et al., 2011; Wahn et al., 2016a). Hence, while adding an additional co-actor would potentially boost joint performance, such an addition would also increase attentional demands placed on co-actors.
Another reason why increasing group size beyond two in a visual search task may not lead to additional benefits is the following. Consider the idealized case of two co-actors who search equally fast when searching alone (e.g., both take 15 s) and who perfectly distribute the search space in two equal halves when searching jointly. In this case, the best possible dyad search performance is a performance that is half of the individual search time (7.5 s) as each co-actor will finish searching half of the search display within that period. For three co-actors, again assuming the same individual search times and a perfect division of labor in three parts, the best possible triad search performance can only result in one-third of the individual search time performance (5 s) as each co-actor will take that time to search one-third of the search display. In other words, the possible benefit for performing a search in a dyad relative to individuals will maximally reduce the search times by half. The possible incremental benefit for performing a search in triads relative to dyads may reduce the search times by maximally one-third.
In sum, when considering these two points (i.e., the rising attentional demands and the lower expected group benefit for triads compared to dyads), it is unclear whether providing co-actors in a triad with gaze information about each other’s actions would still lead to additional benefits.
What we know so far about joint visual search in triads comes from our own earlier study (Wahn et al., 2018a). In this study, participants performed a visual search either alone, in dyads, or triads in a within-subject design. Importantly, while performing the search task co-actors did not receive any information about each other’s actions. The only information that was provided was performance feedback at the end of a trial. We found that dyads outperformed individuals but triads did not significantly outperform dyads. These findings suggest that group benefits do not scale up from dyads to triads when triad members are not provided with information about each other’s actions. However, it is still unclear whether adding gaze information is sufficient for triads to outperform dyads.
In line with other studies (Bahrami et al., 2010; Wahn et al., 2017), we assessed group benefits in our earlier study on triadic visual search by testing (a) whether the dyad’s performance exceeds the performance of the best individual member of the dyad and (b) whether the triad’s performance exceeds the best dyad pairing within each triad. Defined this way, the group benefit is also referred to as a “collective benefit” (Bahrami et al., 2010; Wahn et al., 2017, 2018a). One may propose that the averaged responses (across individuals or dyad pairings) instead of the best individual’s performance or the best dyad pairing, respectively, should serve as a comparison to assess group benefits. Yet, we argued in our earlier study that these comparisons may lead to incorrect conclusions about whether a group benefit is actually attained or not. To illustrate this important point, consider the case of a dyad where the better member of the pair frequently finds the target first. In this case, the joint search performance will be highly similar to the better member’s individual search performance. If one then computes the average of the individual search times, it will be higher than the better member’s individual search time and higher than the actual search time of the dyad. Taken at face value this seems to suggest a group benefit that exceeds the expected value based on the average of the individual performances. But to conclude that there is a real group benefit would be misleading as the better member of the group is not benefiting from performing the search with another (for an in-depth consideration of this type of issue, see Wahn et al., (2018c)). The same logic can also be extended to triads as one dyad pairing within a triad could be driving the effect.
At this point, it is important to consider in some detail how a group benefit may generally arise in this type of task. There are essentially two alternatives. (1) A group benefit can arise when co-actors actively collaborate by dividing the labor. (2) A group benefit can arise when co-actors search independently in parallel. In our previous study where participants did not receive any information about each other’s actions, there was no real possibility for co-actors to collaborate. And by briefing participants after the experiment, we confirmed that they did not use any collaborative strategy such as division of labor. We simulated this non-collaborative/independent joint performance by repeatedly sampling co-actors’ responses from the trial distributions of the individual condition where participants searched alone and then extracting the faster of the two (dyad) or three (triad) responses (Wahn et al., 2018a). The simulated joint performance closely matched the actual joint performance for dyads and triads, thereby confirming that co-actors searched independently and did not collaborate by dividing the labor. Thus, our previous study suggests that two co-actors can achieve a collective benefit simply by acting independently in parallel, yet three co-actors in a triad cannot achieve this benefit when they act independently. We further reasoned that if co-actors attained a joint performance that exceeded the results of our simulation, this would suggest that co-actors did not merely act independently but actively collaborated by distributing the labor. To differentiate this type of group benefit criterion from a collective benefit (that can be attained through independent action), we will refer to this as a “collaborative benefit” (Wahn et al., 2018a). These two criteria allow addressing two different but related questions: The criterion for a collective benefit answers whether a group benefit is attained at all and the criterion for a collaborative benefit answers (2) how this benefit is achieved (through independent action or collaboration).
In sum, our earlier study (Wahn et al., 2018a) addressed group benefits in a dyadic and triadic joint search task using different criteria to address group benefits but it did not examine how the availability of information about each other’s actions affects co-actors’ performance. Given that the availability of action information has been shown to be highly beneficial for dyads in visuospatial tasks (Brennan et al., 2008; Wahn et al., 2017), receiving such information may also enable co-actors in a triad to attain a collective benefit. Alternatively, the higher attentional demands and the lower expected group benefit for triads compared to dyads may offset any potential collective benefits. It is the aim of the present study to test these alternatives. Additionally, we aim to determine whether receiving action information enables co-actors in a triad to actively collaborate and thus attain a collaborative benefit. We also compare the efficiency of potential collaborative strategies and how collaborative strategies may differ between dyads and triads.
While the primary goal of the present study is to investigate whether receiving action information enables triads to attain collective benefits or not, a secondary goal is to also go one step further in our analysis and use a statistical model to assess the contributions of several factors in joint visual search that could predict if, and to what extent, groups attain collective benefits. To date, researchers have investigated several factors that are related to group benefits in visuospatial tasks (for a recent review, see Wahn et al., (2018c)). Yet, an overall statistical model that combines several factors is lacking. Such a model could inform researchers about the relative importance of different factors and to what extent they explain separate or redundant variance when predicting group benefits in visual tasks. More generally, such a model has the potential to serve as a spring board for making predictions in other joint tasks and explaining the observed effects. As a first step towards devising such a statistical model, we use predictors that have been shown to affect or predict group benefits as well as those that are likely to make additional contributions towards predicting group benefits. The variables used in the model encompass categorical variables manipulated in the experiment (i.e., target presence or absence; dyads or triads) as well as continuous variables that vary across dyads and triads (i.e., similarities in individual performances, overlap in search space, & the simulated joint performance that dyads and triads would achieve if co-actors acted independently) (Brennan et al., 2008; Wahn et al., 2017, 2018a).
Materials and methods
Participants
Sixty-three students (48 female, M = 21.9 years) of the University of Osnabrück participated in this study to closely match the sample size and statistical power from our earlier study (Wahn et al., 2018a). The study was approved by the ethics committee of the University of Osnabrück. All participants were informed about their rights, were fully informed on the procedures, had the opportunity to ask open questions and signed a written consent form. Participants either received a monetary reward or course credits for participation.
Experimental setup
The experimental setup consisted of three computer screens (DELL U2713Hb, resolution 2560 × 1440, 60 Hz) placed next to each other. Participants sat at a distance of 100 cm in front of the computer screens. Each participant was in control of one computer mouse (DELL XN966). Seating positions were separated by wooden dividers and participants were asked to wear noise canceling headphones throughout the experiment.
Experimental procedure
Before starting the actual experiment, each participant was randomly assigned to one of three avatars (blue square, purple triangle, or red circle). These avatars were used to index whether participants perform the search alone, in dyads, or in triads and with which co-actors they would perform the search. That is, the computer screen would either display one, two, or three avatars, indicating that the search will be performed alone, in dyads, or in triads, respectively. Moreover, participants were familiarized with the task with 4–8 training trials, in which they randomly either performed the search task alone, in dyads, or in triads.
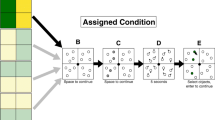
In the experiment, participants were instructed to search for a target object among distractor objects either alone, in dyads, or in triads in a within-subject design. In the search task, the target object was a circle (radius 36 pixels, 0.48 visual degrees) and distractor objects were circles of the same radius with antennas (4 pixels, 0.05 visual degrees) oriented at 0, 90, 180, and 270 degrees. Thirty-six objects were randomly placed within a square frame (1240 × 1170 pixels, 16.62 × 15.68 visual degrees) centered in the middle of the screen. Stimuli were at least 150 pixels (2 visual degrees) apart from each other and in half of the trials the target object was present. The search space was occluded and only a small circular portion, henceforth, referred to as “spotlight”, of the screen was visible for each of the participants. Each participant could move their individual spotlight using the computer mouse to temporarily uncover parts of the screen. All computer mice were set to the same speed and the spotlight was always placed at the position of the computer mouse throughout the experiment. Importantly, when the search was performed in dyads or in triads, each co-actor could see circular outlines of the spotlights of the other co-actors on the computer screen. The outlines of the spotlights of co-actors were colored in the colors of their avatars. That is, each co-actor could see where the other members of the group were looking at the screen when they performed the search task in dyads or triads. However, for each co-actor, the viewed locations by the other co-actors were still occluded and only the space at the position of their own spotlight temporarily uncovered the occluded parts of the screen. To end the search, the participants’ task was to respond using buttons of the computer mouse to indicate whether the target was present (right mouse button) or absent (left mouse button). Importantly, the first response in each condition (i.e., searching alone, in dyads, or triads) ended the search. Participants then received performance feedback, i.e., whether the response was correct or not. Additionally, they were informed which co-actor responded. For an overview of an example trial sequence, see Fig. 1. As a point of note, participants were instructed to respond as fast and as accurately as possible and to collaborate when performing the search in dyads or in triads. Moreover, participants were instructed to not communicate by any means with each other throughout the experiment. That is, the only information participants received from their co-actors was received via the information provided in the experiment. Each participant performed 144 trials comprising 36 trials for each possible combination of co-actors. The order of trials was randomized, yet repetitions of the same conditions in consecutive trials were avoided. The experiment took about 40 min to complete.
Trial logic overview. Displayed is the trial logic from the perspective of a participant assigned with the blue avatar, separately for searching alone (top row), in a dyad (second row), or in a triad (bottom row). At the beginning of a trial, the computer screen would either display one, two, or three avatars, indicating that the search will be performed alone, in dyads, or in triads, respectively. Followed by that, each participant searches for a target among distractors by moving her/his spotlight using the computer mouse. When the search is performed in dyads or triads, participants see the outline of their co-actors’ spotlights (see second and bottom rows, respectively). Participants ended a trial by either indicating that a target is present (right mouse button) or absent (left mouse button)
The experiment was programmed using the Python library pygame (Shinners, 2011) and the experimental procedure and data collection were controlled by Python 2.7.3. The experiment was run on four Dell precision T1700 computers: One server computer coordinating the sequence of events for three client computers, which were connected to the server via network cables.
After measurements were completed, participants filled out a questionnaire, in which they were asked to describe their collaborative strategies (if they had any) when performing the task in dyads or in triads.
Results
Collective benefits for dyads
We first assessed whether dyads attain a collective benefit for the search times. We separated our analysis into target present and absent trials as earlier research on joint visual search found considerable performance differences between these two types of trials (Brennan et al., 2008; Wahn et al., 2018a). To address whether dyads attained a collective benefit and in line with earlier studies (Bahrami et al., 2010; Wahn et al., 2017, 2018a) , we calculated collective benefit ratios for each dyad. In particular, we divided the better member’s mean search time from the individual search condition by the dyad’s mean search time of the dyadic search condition. As smaller numbers, i.e., faster search times, represent better performance, a ratio above one would indicate that a collective benefit was reached. As a general point of note for all other ratios calculated later in this results section, all ratios are calculated in such a way that a value above one would indicate that a benefit is reached. To accommodate the independence of observations assumption required for performing inferential statistical tests, i.e., circumvent the issue that the performance of dyads pairings within a triad are correlated, we averaged across all dyad pairings within a triad. As a result, as the averaged dyad pairings of a triad are independent from the averaged dyad pairings of another triad we can be assured that the independence of observation assumption is fulfilled. Moreover, by averaging across the dyad pairings for each triad, we match our degrees of freedom of the analyses performed on dyads to the analyses performed later on to assess group benefits for triads. Before applying one sample t tests to test whether groups attain a collective benefit, we checked the assumption of normality with a Shapiro–Wilk test. In case of violations of normality, we apply non-parametric comparisons (i.e., Wilcoxon signed-rank test) instead of one sample t tests. We follow the same procedure also for testing collaborative benefits later on. We find a ratio significantly above one both for target present (M= 1.57, SD= 0.18, t(20) = 13.70, p<.001) and target absent (M = 1.55, SD = 0.18, t(20) = 18.82, p<.001) conditions (see Fig. 2a, for a descriptive overview). Thus, we observe a significant collective benefit for dyads.
Collective benefits overview. Mean collective benefit as a function of target presence (absent or present), separately for the search times (dyads in panel a; triads in panel c) and search accuracy (dyads in panel b; triads in panel d). Individual data points are displayed in grey. Error bars in all panels are standard error of the mean
As for the search times, we also calculated collective benefit ratios for the search accuracy (i.e., whether a trial was correctly classified as a target present or target absent trial). That is, we divided the search accuracy of the dyad by the search accuracy of the better member in the dyad. Again, for this ratio, a value above one would indicate that a collective benefit for the search accuracy was attained. For the search accuracy, we observe both for target present (M= 0.90, SD= 0.06, t(20) = -8.23, p<.001) and target absent trials (M = 0.95, SD = 0.06, z = -3.37, p<.001) a ratio below one—see Fig. 2b, for a descriptive overview. Yet, we also observe that the reduction in accuracy is relatively small (10% for target present and 5% for target absent trials) and that the search accuracy performance is generally high for dyads (target present: M = 0.82, SD = 0.07; target absent: M = 0.94, SD = 0.06). Thus, contrary to the search times, dyads performed a significantly less accurate search compared to the better member in a group.
Taken together, for testing whether dyads attain a collective benefit, we find that dyads perform a faster search than individuals. Yet, this search time advantage comes with a cost: Dyads perform a slightly less accurate search than individuals.
To further address this speed–accuracy trade-off, we combined the search times and accuracies into a single measure. In particular, we calculated inverse efficiency scores (Townsend and Ashby 1978, 1983) for each dyad by dividing the mean search times of correct trials by the search accuracies for each dyad. To test whether dyads also attain a collective benefit for the inverse efficiency scores, we calculated for each dyad a ratio by dividing the inverse efficiency score of the better individual member by the inverse efficiency score of the dyad. Again, a score above one indicates that dyads attained a collective benefit when taking into account the speed–accuracy trade-off. Testing these scores against one, we find significant differences for target present (M= 1.51, SD= 0.18, t(20) = 12.51, p<.001) and target absent conditions (M = 1.52, SD = 0.17, t(20) = 13.70, p<.001). In sum, after controlling for speed–accuracy trade-offs, we find that dyads still significantly outperform individuals.
Collaborative benefits for dyads
Attaining a collective benefit, however, does not provide an indication whether dyads also attained a collaborative benefit. For assessing the collaborative benefit, we first simulated a joint performance for each dyad under the assumption that members of a dyad act independently (Wahn et al., 2018a). That is, we aimed to simulate a joint performance that dyads would achieve if they act independently in the search task. For this simulation, for each dyad pairing, we repeatedly drew a trial from each of the two members’ trial distributions when they were searching alone, separately for target present and absent trials. For these two trials, we selected the faster search time of the two and also the corresponding search accuracy. We repeated this procedure a 1000 times and then averaged across the selected trials. As noted in the introduction section, we found in our earlier study (Wahn et al., 2018a) that such a simulation closely matched the actual joint performance of independently acting co-actors in a dyadic visual search task, validating this simulation approach.
To assess whether dyads attained a collaborative benefit, we again calculated ratios by dividing the simulated search performance by the dyad’s actual search times. A ratio above one would indicate that dyads attained a collaborative benefit. To again account for the potential dependence of observations between dyads within a triad, we averaged ratios across the dyad pairings for each triad. We find significant differences from one for target present (M= 1.18, SD= 0.14, t(20) = 5.92, p<.001) and target absent (M = 1.49, SD = 0.12, t(20) = 19.65, p<.001) conditions—see Fig. 3a, for a descriptive overview. These results indicate that dyads collaborated in the present joint search task, enabling them to attain a higher joint performance than the simulated joint performance.
Comparison between simulated independent performance and actual data to assess collaborative benefits. Search times are shown as a function of the actual and simulated data (in a for dyads, in c for triads). Search accuracies are also shown as a function of the actual and simulated data (in b for dyads, in d for triads). The factor target presence is color-coded (and also differentiated by the line type (dashed, for target present; solid for target absent) in all panels. The lines display individual dyads or triads, respectively. Error bars in all panels are standard error of the mean
We repeated this analysis also for the search accuracies. That is, we again calculated ratios by dividing the dyad’s actual accuracy performance by the simulated accuracy performance. Again, a ratio above one would indicate that dyads attain a collaborative benefit with regard to the search accuracies. Accounting for the potential dependence of observations between dyads within a triad, we averaged across the ratios of the dyad pairings for each triad. We find that dyads performed the search significantly less accurately than individuals when the target was present (M= 0.90, SD= 0.06, t(20) = -7.49, p<.001). However, we found no significant differences when the target was absent (M= 0.99, SD= 0.06, t(20) = -0.63, p=.534).
As for the collective benefit, to address this speed–accuracy trade-off, we also investigated inverse efficiency scores for the collaborative benefit. For this purpose, we calculated inverse efficiency scores also for the simulated dyad performances. To assess whether dyads attain a collaborative benefit, we divide the inverse efficiency scores based on the simulation by the actual inverse efficiency scores of the dyads. Again, to account for the potential dependence of observations between dyads within a triad, we averaged across the ratios of the dyad pairings for each triad. Testing these ratios against one, separately for the target present and absent conditions using one sample t tests, we find that dyads attain a collaborative benefit for the target absent condition (M= 1.41, SD= 0.16, t(20) = 11.29, p<.001) but not for the target present condition (M = 1.03, SD = 0.13, t(20) = 1.08, p=.293). These findings suggest that the search time benefits of collaborating do not outweigh the accuracy costs for the target present condition. Yet, as noted above for the collective benefit, dyads still attain a collective benefit after taking into account speed–accuracy trade-offs. For the target absent condition, as noted above, there were no significant accuracy costs when comparing the dyads’ performance to the simulated joint performance and also after accounting speed–accuracy trade-offs, dyads still attain a collaborative benefit.
Collective benefits for triads
For triads, we repeated the same analysis as above for dyads. That is, we tested whether triads attained a collective benefit and a collaborative benefit for the dependent variables search time and search accuracy. As in our earlier study (Wahn et al., 2018a), we extended the definition of a collective benefit for triads by comparing the triads’ performance to the best dyad pairing within the triad. That is, to calculate collective benefit ratios, we divided the search time of the best dyad pairing from our dyadic search condition within a triad by the search time of the triad from our triadic search condition. As above, a value above one would indicate that triads attained a collective benefit. We observe a ratio significantly different from one both for target present (M= 1.20, SD= 0.21, t(20) = 4.53, p<.001) and target absent (M = 1.12, SD = 0.10, z = 3.98, p<.001) conditions (see Fig. 2c, for a descriptive overview). Thus, triads are able to attain a collective benefit in the present experimental conditions.
For the search accuracies, analogously as for the calculations for the dyads above, we divided the search accuracy of the triad by the best dyad’s search accuracy. Again, a value above one would indicate that dyads attained a collective benefit. As for the dyads above, we find that triads perform a significantly less accurate search compared to the best dyad pairing in a group, both for target present (M= 0.93, SD= 0.12, t(20) = -2.42, p=.025) and target absent trials (M = 0.96, SD = 0.06, z = -2.21, p=.026)—see Fig. 2d, for a descriptive overview. As above for the dyads, we also observe that these accuracy reductions are again relatively small (7% for target present trials; 4% for target absent trials) and the accuracy performance of triads is generally quite high (target present: M = 0.85, SD = 0.10; target absent: M = 0.94, SD = 0.05).
To address this speed–accuracy tradeoff, we again combined the search times and accuracies into one measure by calculating inverse efficiency scores (Townsend & Ashby 1978, 1983). In particular, we divided the mean search time of correct trials by the search accuracies for each triad. We also calculated inverse efficiency scores for each dyad pairing. To test whether triads attain a collective benefit, we calculated for each triad a ratio by dividing the inverse efficiency scores of the best dyad pairing by the triads’ inverse efficiency scores. Testing these ratios against one, we find that triads significantly attain a collective benefit both for target present (M= 1.18, SD= 0.24, t(20) = 22.73, p<.001) as well as target absent conditions (M = 1.10, SD = 0.11, t(20) = 45.46, p<.001). That is, taking into account the speed–accuracy trade-off, we find that triads still attain a collective benefit.
Collaborative benefits for triads
As above for the dyads, we also investigated whether triads attain a collaborative benefit. For this purpose, we again simulated a joint performance under the assumption that members of a group act independently. We repeatedly drew one trial from each of the triad’s members individual performance trials (i.e., when each member performs the search task alone). Out of these three trials, we select the trial with the fastest performance and the corresponding accuracy (i.e., correct or incorrect response). Again, we repeat this procedure a 1000 times and average across the selected trials, separately for each triad. The reasoning is that if members of a triad would perform the search task independently, the participant who responds first will end a trial. Hence, selecting the fastest out of three randomly selected trials from the individual distributions will approximate a joint performance that a triad would reach if they perform the task independently. As noted in the introduction section, we found in our earlier study (Wahn et al., 2018a) that such a simulation closely matched the actual joint performance of independently acting co-actors in a triadic visual search task, validating this simulation approach.
To assess whether triads attained a collaborative benefit, we again calculated ratios by dividing the simulated search performance by the triad’s actual search performance. A ratio above one would indicate that triads attain a collaborative benefit. We find a ratio significantly larger than one both for target present (M= 1.27, SD= 0.26, t(20) = 4.66, p<.001) as well as target absent (M = 1.65, SD = 0.22, t(20) = 13.69, p<.001) trials. Thus, triads also attain a collaborative benefit.
We repeated this analysis also for the search accuracies. That is, we again calculated ratios by dividing the triad’s actual performance by the triad’s simulated accuracy performance. Again, a ratio above one would indicate that triads attain a collaborative benefit with regard to the search accuracies. In line with the findings above on the collective benefit, we find that triads perform significantly less accurately compared to the simulated triad’s accuracies for the target present (M = 0.90, SD = 0.10, t(20) = -4.60, p<.001) but not for the target absent condition (M = 1.01, SD = 0.10, z = -0.12, p=.911).
As for the collective benefit, to address this speed–accuracy trade-off, we calculated inverse efficiency scores for the simulated triad performances and actual triad performances. To assess whether triads attain a collaborative benefit, we divide the inverse efficiency scores for the simulation by the actual inverse efficiency scores of the triads. We again tested these ratios against one, separately for the target present and absent conditions. We find that triads attain a collaborative benefit both for the target absent (M= 1.58, SD= 0.25, t(20) = 10.68, p<.001) and the target present condition (M = 1.17, SD = 0.27, t(20) = 2.93, p=.008).
In sum, we find a similar pattern of results for the triads as for the analysis of the dyads’ collaborative benefit above. For the search times, triads do attain a collaborative benefit. With regard to the search accuracy, triads are significantly worse than the simulated independent performance for target present condition while they attain comparable accuracy levels for the target absent condition. Yet, when taking into account this speed–accuracy tradeoff, we find that triads still attain a collaborative benefit, both for the target present and target absent condition.
Comparisons between group sizes
In addition to the analyses above on the collective and collaborative benefit, we also compared whether the collective benefit ratios with regard to the search times and search accuracy would differ between dyads and triads and whether the target presence would influence such differences. That is, instead of testing whether a collective benefit is attained or not, we here compare the magnitude of the collective benefits between group sizes. We perform these comparisons to assess whether the group benefits gained by searching in dyads (compared to searching alone) are comparable to the group benefits gained by searching in triads (compared to searching in dyads).
For this purpose, we performed a 2×2 repeated measures ANOVA with the factors Target Presence (absent, present) and Group Size (dyads, triads) with the collective benefit ratios for the search times as the dependent variable. We find a main effect of Group Size (F(1,20) = 113.11, p <.001) but neither a main effect of Target Presence (F(1,20) = 2.02, p=.170) nor an interaction between the factors (F(1,20) = 0.94, p <.342). These results suggest that with increasing group size, collective benefits for the search times become smaller (for a descriptive overview, see Fig. 4). To have an estimate by how much the collective benefit decreases, we computed the mean collective benefit across the levels of the factor target presence and calculated a ratio between the mean collective benefits of dyads and triads. We find the collective benefit is reduced by 25% (dyads: 1.56 vs. triads: 1.16). In sum, these findings suggest that with increasing group size, the gain in performance becomes smaller.
We repeated this analysis also for the collective benefit ratios of the search accuracies as the dependent variable using again a repeated measures ANOVA with the factors Group Size and Target Presence. We find a main effect of Target Presence (F(1,20) = 7.51, p =.013) but we neither find a significant effect of Group Size (F(1,20) = 1.34, p=.261) nor a significant interaction effect (F(1,20) = 0.45, p =.509). Taken together, we find that dyads attain a higher collective benefit than triads with regard to the search times and find no significant differences for the search accuracies.
As a point of note, one could argue that a comparison of collective benefits based on the search times between group sizes may not be a fair comparison as the group benefit is a priori expected to be lower for triads than for dyads. As noted in the introduction, assuming a perfect division of labor and equal individual search times, co-actors in a dyad have the possibility to halve their joint search times compared to individual performing. Triads on the other hand, again assuming equal individual search times and a perfect division of labor, can only reduce the search time by one-third relative to dyads. To use a performance measure that would circumvent this issue, we also calculated the dyads’ and triads’ search speeds. Contrary to the search times, we reasoned that for this measure the maximum expected gain in speed of searching visual space for each increase in group size should be equal. For instance, consider the example that all members in a group search equally fast (e.g., 10 deg2/s), then again given a perfect division of labor, dyads would attain a performance of 20 deg2/s and triads of 30 deg2/s. Hence, the joint search speed would scale linearly with group size. To compare the dyads’ and triads’ search speeds, we calculated the search speeds for all conditions (individuals, dyads, triads) by dividing the searched area by the search time for each trial. For comparing the gains in group benefit, we calculated collective benefit ratios using the search speeds. That is, for dyads, we divided the search speed of each dyad by the fastest individual search speed within the dyad. For triads, we divided the triad search speeds by the fastest dyad pairing within a triad. Again, ratios above one indicate a collective benefit.
On a descriptive level (see Fig. 5), we find a similar pattern of results as for the collective benefit based on the search times. That is, dyads attain a higher collective benefit than triads, again suggesting smaller gains with increasing group size. We tested whether these observations are statistically reliable again with a 2×2 ANOVA with the factors Group Size and Target Presence and the dependent variable collective benefit. We find a main effect of Group Size (F(1,20) = 223.13, p<.001) and a main effect of Target Presence (F(1,20) = 91.42, p <.001). In addition, we find a significant interaction effect (F(1,20) = 10.65, p=.004). These findings again suggest that dyads attain a higher collective benefit compared to triads. In addition, given the significant interaction effect, the higher benefit for dyads (relative to triads) is larger for target present trials compared to target absent trials.
Collaborative strategies
As a next step we investigated whether co-actors used collaborative strategies and when this was the case also compared the efficiency of the strategies between dyads and triads.
To address whether groups used collaborative strategies, we assessed participants’ answers in the questionnaire and found that 90.5% of the participants indicated that they used a strategy when collaborating with one partner. In all these cases, participants wrote that they divided the labor. The same is true for triads. Yet, the percentage of participants that indicated using a strategy is slightly lower 86%. Out of these, 14% of the participants indicated that they experienced difficulties forming strategies in triads. A typical example is starting out with a chaotic search that developed into a division of labor strategy.
To quantify the efficiency with which such division of labor strategies were used, we calculated the fraction of overlap in the searched spaces. That is, we overlaid the searched spaces by all co-actors and calculated the area of overlap. Dividing this overlap by the total search area of all co-actors results in the fraction of overlap. The interpretation for this measure is that co-actors who did distribute the labor efficiently should have a low fraction of overlap close to zero whereas co-actors who did not distribute the labor efficiently should have a high fraction of overlap approaching unity. We compared the fraction of overlap for all combinations of the factor Group Size (dyads vs. triads) and Target Presence (absent vs. present)—for a descriptive overview, see Fig. 6a. Visually inspecting the data, it appears that co-actors are generally less efficient in dividing the labor when searching in a triad compared to a dyad. Generally, co-actors also tend to search less efficiently in target absence trials compared to target presence trials. Moreover, the difference between dyads and triads appears to be larger for target absent trials compared to target present trials. We tested whether these observations are statistically reliable using a 2×2 repeated measures ANOVA with the factors Target Presence and Group Size. In line with our observations, we find significant main effects of Target Presence (F(1,20) = 131.12, p<.001) and Group Size (F(1,20) = 145.97, p <.001), and a significant interaction effect (F(1,20) = 78.48, p <.001).
In sum, our results suggest that dyads and triads used division of labor strategies and that the efficiency with which they used these strategies depended on the group size and whether a target was present or absent.
As a point of note, one could argue that a lower efficiency of the search strategies for triads compared to dyads should be expected as there is (given the limited search space) simply a higher chance for triad members to overlap with their spotlights compared to dyad members. To address this potential critique, we calculated another measure to compare the efficiency of strategies between dyads and triads based on the search speed performance measure introduced in the section above. In particular, using the individual search speeds, we can calculate an estimate of the area maximally covered per unit time for dyads and triads under the assumption of a perfect division of labor strategy. To calculate this estimate, we added the individual search speeds of co-actors for dyads and triads, respectively. For comparing the real performance to this estimate, we divided the actual search space covered by the estimated maximum search space covered per unit time. For these ratios, a value of one would indicate that groups attained the estimated maximum search space covered based on the individual performance. We reasoned that if co-actors in a triad are not affected by the additional attentional load to distribute the search with two co-actors, then triads should be as close as dyads to the estimated maximum.
For these ratios, however, we observe a similar pattern as for the overlap measure above (see Fig. 6b, for a descriptive overview). That is, compared to triads, dyads are generally closer to attaining the estimated maximum search space covered or even surpass it. Moreover, again, there appears to be a main effect of Target Presence and an interaction effect between the factors Group Size and Target Presence. We tested whether these observations are statistically reliable using a 2×2 repeated measures ANOVA with the factors Target Presence and Group Size. In line with our observations, we find significant main effects of Target Presence (F(1,20) = 120.32, p<.001) and Group Size (F(1,20) = 155.77, p <.001), and a significant interaction effect (F(1,20) = 33.91, p <.001). In sum, these findings confirm our results above for the overlap measure.
Besides comparing dyads and triads for these ratios, we also observe that dyads and triads attain the estimated maximum area covered per unit time and to a degree even surpass it in case of dyads while this is not the case for the target absent trials. Using one sample t tests testing against one, we tested whether these observations are statistically reliable. For dyads and triads, we find that the ratios were significantly below one for the target absent condition (dyads: t(20) = -9.93, p<.001; triads: t(20) = -19.80, p <.001) and did not significantly differ from one for the target present condition (dyads: t(20) = 1.60, p=.125; triads: t(20) = -1.99, p =.061). Given we found that dyads and triads did not perfectly divide the labor (when analyzing the fraction of overlap above), these results suggest that dyad and triad members individually searched faster in a dyad and triad than when performing the search task alone.
To follow up this suggestion, we specifically assessed whether the individual search speeds increase when participants perform the search jointly. For this purpose, we calculated ratios by dividing the search speed of each co-actor in a dyad (and triad) by the search speed obtained when performing the search task alone. On a descriptive level (see Fig. 7), we find that participants individually search about 10% faster in a dyad and triad than when searching alone. We tested whether these observations are statistically reliable using a one sample t test and testing against one. We found that the search speed increase is significant for all conditions (dyads target absent: t(20) = 4.27, p<.001; dyads target present: t(20) = 5.91, p <.001; triads target absent: t(20) = 3.71, p =.001; dyads target absent: t(20) = 5.12, p <.001). These findings suggest that participants increase their individual search speed once they perform the search task jointly. Given that we above found small reductions in search accuracy for dyads and triads, these findings suggest that the accuracy reductions are due to a speed–accuracy tradeoff.
We further investigated this speed–accuracy tradeoff by testing whether or not accuracy reductions can be attributed to specific group members (e.g., the slower of the two members) or not. For this purpose, we analyzed the search accuracies of each group member when visual search was performed jointly. The group members’ were differentiated based on their individual performances. That is, for dyads, we differentiated between the slower and faster member. For triads, we differentiated between the slowest, middle, and fastest member. We compared the search accuracies using a two factorial ANOVA with the factors Target Presence and Member Performance (for dyads: slower, faster; for triads: slowest, middle, fastest). For dyads, we found a significant main effect of Target Presence (F(1,20) = 21.75, p<.001) but, critically, no significant effect of Member Performance (F(1,20) = 0.90, p=.353) or interaction effect (F(1,20) = 0.02, p =.885). For triads, we found no significant effects (main effect of Member Performance: F(2,30) = 1.51, p=.238; main effect of Target Presence: F(1,15) = 1.60, p =.226; interaction effect: F(2,30) = 3.02, p =.064). We calculated Bayes factors for the non-significant main effects of Member Performance. For dyads, we found that the null hypothesis is about three times more likely than the alternative hypothesis (Bayes Factor: 2.94). For triads, we found that the null hypothesis is about two times more likely than the alternative hypothesis (averaged Bayes Factor for all pairwise comparisons: 2.25). These results suggest that the reductions in accuracy (when search is performed jointly) cannot be attributed to specific group members.
Next, we investigated how co-actors distributed the labor. Essentially, there are two alternatives: (1) Co-actors distribute the labor in line with the individual search capabilities of the co-actors. For example, for dyads, the faster member based on the individual search time performances searches a larger space than the slower member, so that both members of the dyad would finish their individual search space at the same time. (2) Co-actors may divide the search space equally, irrespective of differences in speed of search. To assess which type of division of labor strategy was used by dyads and triads, we plotted the fraction of the total searched space as a function of group members sorted by the individual search times—see Fig. 8. In other words, we assessed how much of the searched space was searched by each individual in the group. On a descriptive level, we find that co-actors tend to distribute the search space equally for dyads whereas for triads the search space is distributed in accordance with the individuals’ search time performances. That is, the fastest member (based on the individual performance) searched the largest space in the triad condition followed by the second fastest member and slowest member. We tested whether these observations are statistically reliable by running two repeated measures two-way ANOVA with the factors Target Presence and Member Performance—one for dyads and one for the triads. For dyads, the factor Member Performance had two levels (faster, slower) while for triads the factor Member had three levels (fastest, middle, slowest). For dyads, we only found a main effect of Target presence (F(1,20) = 110.64, p<.001) but no significant main effect of Member Performance (F(1,20) = 0.16, p=.695) and no significant interaction effect (F(1,20) = 1.52, p =.232). With regard to the main effect of Member Performance, we additionally computed a Bayes Factor to assess how more likely the null hypothesis (i.e., the searched areas are equal for the faster and slower member) is compared to the alternative hypothesis (i.e., the searched areas differ in size). We find a Bayes Factor of 4.09, meaning that the null hypothesis is 4.09 more likely than the alternative hypothesis. These findings suggest that dyad members distribute the search space equally and independent of the individual performances.
For triads, we found a significant main effect of Target Presence (F(1,20) = 110.64, p<.001) and of Member Performance (F(2,40) = 9.27, p <.001) but no significant interaction effect (F(2,40) = 2.12, p <.133). To follow-up the significant main effect of Member Performance, we first averaged the data across the levels of the factor Target Presence and then computed a correlation for each triad with the variables fraction of searched area and the factor Member Performance as an ordinal variable. We then tested these correlations against zero using a one-sample t test and found they significantly differ from zero (t(20) = 2.94, p<.008, mean r=.42). These findings suggest that triad members tend to distribute the searched space in accordance with their individual search time performances whereas dyads distributed the searched space equally.
Linear model to predict group benefits
As a next step, we investigated to what extent several predictors contribute towards explaining variance in the extent of group benefits. For this purpose, we first fitted a linear mixed model using the predictors Target presence (absent, present) and Group size (dyads, triads) to predict the collective benefit for the search times. We also included in this model random intercepts (for groups) and slopes (for the factors Target presence and Group size and their interaction term). In particular, the random intercepts accounted for the fact that participants are nested within groups and the random slopes modeled the effects of our experimental factors (and their interaction) for each group. This model we consider as our “baseline” model as it incorporates only the experimental conditions in the present study.
We then assessed the contributions towards explaining additional variance by the predictors fraction of overlap, individual performance similarities, and the simulated independent performance. We selected these continuous variables as predictors as they focus on different aspects of joint visual search performance and hence complement each other. In particular, the overlap in search space we view as an indicator of how well co-actors distribute the labor in the joint visual search task. Hence, we consider it as a predictor of how well co-actors collaborate in the joint search task. The simulated independent performance, in contrast, is a predictor of the group benefit dyads and triads would achieve if they act independently. Hence, we view it as a predictor of the group benefit in the absence of collaboration. Finally, the predictor individual performance similarities may yet explain another complementary set of variance in predicting group benefits. That is, as the data for the performance similarities is collected in the individual conditions, the variance explained by this predictor may also be complementary to the predictor quantifying the collaboration between co-actors or the simulated independent performance. Given this reasoning, we predict that all these predictors make non-redundant contributions towards explaining variance in group benefits.
The independent performance was simulated following the same procedure as outlined above in the analyses on the collaborative benefit for dyads and triads. The overlap in search space was calculated as noted above in the section on collaborative strategies. The performance similarities were calculated by taking the standard deviation across the mean individual search time performances of the members of a group.
We added the predictors fraction of overlap, performance similarities, and the simulated independent performance as well as their respective interaction terms with the other predictors in all possible combinations to the model and evaluated each addition using model comparisons using likelihood ratio tests. The rationale for performing these stepwise additions to the model was to assess the extent that the added predictors could explain additional variance in the data. In particular, this allowed us to compare the increases in explained variance between different added predictors. For these model comparisons, we used the Bayesian Information Criterion as it is a measure of how well a model fits the data, which is corrected for the number of included predictors. To provide a measure of the model fit on a normalized scale, i.e., to assess the variance explained, we calculated R2 for all models (Bartoń, 2018; Nakagawa & Schielzeth, 2013; Johnson, 2014). As we fitted linear mixed models, there are two R2 calculations available (Nakagawa & Schielzeth, 2013; Johnson, 2014), one only taking into account the fixed effects (“marginal R2”) and one also taking into account the random effects (“conditional R2”). We here report the marginal R2 in an overview figure below.
The baseline model explains already a sizeable fraction of the variance (R2 =.36). For the model comparisons, in a first step, each of the continuous predictors together with the interaction terms with the other predictors is separately added to the baseline model. We find that adding the performance similarities predictor (χ2(4)= 36.79, p<.001, BIC = 31.73), the independent performance predictor (χ2(4)= 26.22, p <.001, BIC = 42.30), and fraction of overlap predictor (χ2(4)= 49.01, p <.001, BIC = 19.51) are all significant additions to the model. When comparing the R2 in this modeling step, we observe that the greatest improvement of the explained variance relative to the baseline model is found for the fraction of overlap variable (R2 =.51) followed by the performance similarities (R2 =.48) and the simulated independent performance (R2 =.45).
In a second step, we tested all combinations of adding these predictors relative to models when only one of the continuous predictors is included and find that all these additions were significant as well. In particular, for a model that includes both the performance similarities and independent performance predictor, we find that it is a significant improvement relative to a model only containing the performance similarities predictor (χ2(8) = 29.93, p<.001, BIC = 42.79) or independent performance predictor (χ2(8) = 40.50, p<.001, BIC = 42.79). Likewise, for a model that includes the independent performance predictor and overlap predictor, we find that this model is a significant improvement relative to a model only containing the independent performance predictor (χ2(8) = 58.70, p<.001, BIC = 1.80) or overlap predictor (χ2(8)= 81.49, p <.001, BIC = 1.80). And finally, for a model that includes the performance similarities predictor and overlap predictor, we find that this model is a significant improvement relative to a model only containing the performance similarities predictor (χ2(8)= 54.55, p<.001, BIC = 5.95) or overlap predictor (χ2(8)= 77.34, p <.001, BIC = 5.95). Comparing the explained variance between models at this stage, we find that models containing the overlap predictor attained the highest variance (overlap & independent performance: R2 = 0.62; overlap & performance similarities: R2 = 0.63) while the model containing the performance similarities predictor and independent performance predictor attained a slightly lower explained variance (R2 = 0.55).
In a final step, we assessed the improvement in the model fit by comparing a model with all continuous predictors included compared to models including only two of them. Also for this final step, all model comparisons were significant. That is, the full model represented a significant increase in the variance relative to a model only incorporating the individual performance similarities and independent performance as predictors χ2(16)= 93.66, p <.001, BIC = 31.12), the individual performance similarities and overlap predictors (χ2(16)= 56.82, p <.001, BIC = 31.12), and independent performance and overlap predictors (χ2(16)= 52.67, p <.001, BIC = 31.12). Collectively, these results suggest that all continuous predictors make non-redundant contributions towards explaining additional variance for collective benefits (for an overview, see Fig. 9). The final model also explains more variance than all other models (R2 = 0.70). Yet, we also want to note that from the perspective of the BIC, i.e., a model fit criteria penalizing the number of predictors in a model, a model only with the continuous predictors overlap and the independent performance (in addition to the categorical predictors) attains the best model fit (BIC = 1.80).
Explained variance overview. Displayed are R2 for each model. The “full model” (all continuous predictors and all interactions added) explains an additional 35% of variance relative to the “baseline model” (only including the categorical predictors target presence and group size). Note, all model comparisons are significant
To further evaluate the model fit of the final model including all continuous predictors, we computed the root-mean-square error (henceforth abbreviated as “RMSE”) between the actual collective benefit and the predicted collective benefit of the model (see Fig. 10b). That is, for each data point we computed the difference between the actual collective benefit and the predicted collective benefit and squared these differences. We then sum up these squared differences, divided the sum by the number of data points, and took the square root of the result. We observe that the model closely predicts the actual values (for comparison, we also plotted the predictions of the baseline model in Fig. 10a). In addition, we also computed the RMSE for the model with the best BIC (i.e., the model only including the continuous predictors overlap and independent performance) and found that it is only slightly worse compared to the full model (0.12 vs. 0.11).
Predicted vs. actual collective benefit. The actual collective benefit is plotted on the ordinate whereas the predicted collective benefit is plotted on the abscissa, separately for (a) the baseline model and (b) the full model. For both plots, we noted the RMSE. Adding the continuous predictors (and all possible interactions) leads to a prediction error decrease of 47%
Discussion
In the present study, we investigated whether collective benefits obtained for dyads that receive action information of co-actors also scale up to triads. We found that with regard to the search times dyads and triads outperform the best member in the group and outperform the best dyad pairing, respectively, i.e., they do attain a collective benefit. Yet, these benefits come with a cost: Dyads and triads perform a slightly less accurate search than individuals and dyads, respectively. Critically, when speed–accuracy tradeoffs are controlled for, we find that dyads and triads continue to demonstrate a collective benefit. We also discovered that dyads and triads achieve their collective benefits with regard to the search times through collaboration. With regard to collaborative strategies, we find that both dyads and triads devise division of labor strategies but the efficiency of these strategies was better for dyads than for triads. Yet, we also found that co-actors distributed task demands more in line with their individual search performances when searching in triads compared to searching in dyads. Further, we compared the extent of the group benefit between dyads and triads and found that dyads attained a higher benefit than triads. Finally, we investigated the separate contributions of several predictors of the collective benefit in an overall model to assess the extent that the predictors are efficient or redundant. The predictors included the categorical variables manipulated in the present experiment, i.e., target presence and group size, and continuous predictors, i.e., individual performance similarities, the simulated independent performance, and the fraction of overlap. We find that all predictors make non-redundant contributions towards predicting group benefits, accounting for a total of 70% of the variance. In the following, we discuss each of our findings in turn.
Our finding that after taking into account speed–accuracy tradeoffs triads attain a collective benefit with regard to the search times extends earlier findings on joint visual search by showing that this effect is not limited to groups of two individuals (Brennan et al., 2008). Moreover, our findings also demonstrate that these benefits are dependent on the sharing of action information between co-actors as without such information co-actors in a triad were not able to attain a collective benefit in our earlier study (Wahn et al., 2018a). In addition, our results suggest that the benefits of receiving action information outweigh the coordination costs and the reduced possible extent of group benefits for triads. More generally, these findings further corroborate the previous suggestion that receiving action information of co-actors is an important factor to enable groups to attain group benefits in joint search tasks (Brennan et al., 2008). Relatedly, the availability of action information of co-actors has also been identified as an important factor contributing to group benefits in a different dyadic joint visuospatial task (Wahn et al., 2017) and also in a joint motor task (Knoblich & Jordan, 2003).
With regard to our finding that dyads and triads perform a slightly less accurate search than individuals and dyads, respectively, we suggest that this loss in accuracy is likely due to an increase of individual search speeds in the joint condition relative to the individual condition. That is, we found that co-actors had higher individual search speed in the dyad and triad condition compared to performing the search task alone. As a result of this increase in individual search speeds, co-actors sacrificed performance accuracy in the joint conditions. Potentially, performing the visual search jointly led co-actors to be more motivated (or pressured) and as a result individual search speeds increased. Alternatively, the mere social presence of other co-actors (indicated by the other spotlights displayed on the computer screen) may have resulted in higher individual search speeds rather than joint task performance. Relatedly, research on social facilitation and impairments effects has investigated how the mere presence of another person can improve or worsen performance compared to performing the same task alone (for a recent review, see Belletier et al., (2019)). Future studies may test whether the increase in the individual search speeds and drop in search accuracy in the present visual search task is due to the mere presence of others or due to performing a task jointly. In particular, it could be the case that an increase in the individual speeds is already attained if the presence of other humans are indicated on the computer screen, which do not participate in the joint search task.
Apart from finding that co-actors in dyads and triads attain collective benefits, both our findings that dyads and triads attain a collaborative benefit and that they self-report using division of labor strategies, provide converging evidence that co-actors are collaborating in the present joint search task (Wahn et al., 2018a). To quantify the efficiency with which co-actors in dyads and triads divided the labor, we analyzed the extent that search spaces of co-actors overlap. As noted above, dyads were more efficient than triads in distributing their labor. These findings suggest that co-actors in dyads may find it easier to keep track of where their co-actor already searched, whereas for co-actors in triads it may be more difficult to track the movements of their co-actors. Moreover, these findings may provide an explanation for why increasing the group size in joint visual search led to lower gains in group benefits. That is, while adding group members to the group does increase the perceptual capacity to search for a target, it also increases attentional demands as co-actors need to track where two co-actors are currently searching. Consistent with this line of reasoning, a small fraction of the participants reported having more difficulty distributing their labor when in triads. Alternatively, co-actors may have found it less intuitive to distribute the labor in a triad compared to a dyad.
Future studies could seek to discover the point at which adding more co-actors no longer leads to additional group benefits; as the boosts in group performance may no longer compensate for the increasing coordination costs and the diminishing possible extent of a group benefit. To attenuate the rising coordination costs, larger groups may start to subdivide themselves into smaller subgroups. For instance, a group of four co-actors may subdivide themselves into two dyads and one of the dyads may use a left-right division of labor strategy for the top part of the screen, while the other dyad may use a left-right division of labor strategy for the bottom part of the screen. Relatedly, groups of different sizes may find it easier to distribute the labor if the search display offers an intuitive division of labor. For instance, triads may find it easier to distribute the labor if the search display is shaped in a triangle as each co-actor could search in one corner whereas quadruples may prefer a quadratically shaped search display. Apart from the screen shape, the size of the screen is of course another factor that may affect coordination costs. For example, it seems reasonable that a relatively larger screen than the one used in the present work may require less coordination between group members to efficiently distribute their labor. Regardless of screen shape or size, coordinations costs could also be attenuated by explicitly indicating the division of labor strategy for the group members. For instance, the search space could already contain dividing lines indicating the assigned search space for each group member. Yet another way to attenuate coordination costs may be to allow group members to verbally communicate before they are performing a search trial together. That is, group members could negotiate in advance a division of labor strategy that does not require any monitoring of co-actors while performing the search.
While the increased attentional demands for triads resulted in less efficient search strategies and a lower extent of the collective benefit, we also find that the division of labor for triads were more in line with the individual search time performance of the triad members compared to the distribution of labor for dyads. That is, in triads the fastest co-actor based on the individual search time performances searched a larger space than the second fastest member and slowest member. In comparison, for dyads the search space was divided approximately equally. As noted above, given that participants indicated having more difficulty distributing their labor when in triads, we suggest that co-actors in a triad may have followed a less structured division of labor strategy, e.g., by generally trying to avoid each other’s spotlights. In contrast, co-actors in a dyad may have followed a more structured division of labor search strategy, e.g., each co-actor searches one half of the display. However, co-actors in a dyad apparently assumed similar individual search abilities and as a result distribute the search space equally. In the more “chaotic” search in a triad, a strategy as simply avoiding each other probably led to a more redundant search but also a distribution of the searched space that is more in line with the triad members’ individual search abilities. Our finding that dyads distribute the search space roughly equally dovetails with recent findings in a collective perceptual decision-making task (Mahmoodi et al., 2015), in which researchers found that co-actors tend to assume that they have similar perceptual capabilities. Future studies could test whether such an “equality bias” (Mahmoodi et al., 2015) also extends to capabilities other than perceptual capabilities such as, for instance, motor capabilities in joint motor control tasks (Wahn et al., 2018b) or memory capabilities in joint memory tasks (Rajaram and Pereira-Pasarin, 2010). Moreover, as division of labor strategies that more optimally make use of the individual capabilities of participants likely would result in a better group performance, future research could test how co-actors may circumvent such a bias and instead accurately assess individual performance capabilities in the group.
As a point of note, one may question whether the division of labor strategies by triads constitute a form of collaborative behavior, as it may only involve that co-actors avoid each other’s searched space. We suggest that co-actors still collaborate in these cases as they still coordinate their actions in time and space and share a common goal (i.e., facilitating the search performance) (Sebanz et al., 2006; Vesper et al., 2017). On this note, it would be interesting to conduct a future study that examines how quickly division of labor strategies are devised over time, and whether there are differences in learning rates between dyads and triads. In the present study, the trials for all the conditions were randomly interleaved, compromising our ability to separate the learning rates for each condition. Placing the different conditions (search alone, in a dyad, or in a triad) in separate experimental blocks could address this issue in the future.
Apart from addressing the question whether triads attain a collective and collaborative benefit, we also investigated a number of predictors of the collective benefits in a linear model. These predictors include the overlap in the searched space by the co-actors, similarities in the individual performances, and simulated independent search performance. We chose these predictors as we hypothesized that each of them would provide a non-redundant contribution towards predicting the collective benefit. Investigating the contributions of each predictor separately, we found that the search-space overlap makes the highest contribution towards predicting the collective benefit. This is followed by performance similarities, and finally, the simulated independent search performance. These findings suggest that the predictor search-space overlap quantifying the collaboration between co-actors explains more variance in group benefits than the predictors individual performance similarities and simulated independent performance, which are unrelated to the benefits received through collaboration. In other words, differences in the extent of attained group benefits depend more on the collaboration between co-actors than how well they perform the task individually and to what extent they achieve “independent” benefits by merely performing a task jointly. In addition, we found that all subsequently added predictors make non-redundant contributions towards predicting a collective benefit. These findings suggest that all the predictors are relevant to an enhanced understanding of how group benefits in joint visual search tasks come about. The final model including all predictors also explains more than two thirds of the variance in the data, suggesting that the present set of predictors captures much of the relevant variables group benefits in the present joint visual search task.
Future studies may seek to refine our current model by adding additional non-redundant predictors to account for some of the residual variance in the data. For instance, a future study could assess the role of verbal communication as opposed to receiving action information in predicting group benefits. Other non-redundant predictors might include personality traits of the group members, e.g., those relevant to social cognition such as empathy (Czeszumski et al., 2019; Davis, 1983). Moreover, future studies could test to what extent the predictors used in the present model are applicable to other joint tasks. For instance, in perceptual decision-making tasks (Bahrami et al., 2010) and joint motor control tasks (Wahn et al., 2016b), performance similarities have been found to contribute to the prediction of group benefits. The simulated independent performance and measures of how well co-actors collaborate may also provide a complementary set of predictors for group benefits in perceptual decision-making and motor tasks.
More generally, it is worth noting that the present findings may also be applicable to a number of real-life scenarios or professions that are conceptually similar to the visual search task used in the present study. For instance, one scenario could involve people jointly searching web content while the eye movements of co-actors (tracked via webcams (Papoutsaki et al., 2016)) are displayed on the computer screen. More generally, people frequently perform tasks collaboratively online in remote locations that involve information about a co-actors’ actions (e.g., working collaboratively on a manuscript in real-time involves seeing another person’s additions and deletions of text). In such scenarios, small or large groups of people, may also start to distribute their labor to effectively perform tasks jointly. With regard to professions that perform search tasks on a daily basis, airport security personnel are required to scan luggage for dangerous items and radiologists base their diagnoses in part on what they may or may not detect in medical images. In such situations, the speed with which such tasks are completed may be increased by having several co-actors perform these tasks jointly. In particular, joint performance may be facilitated by displaying the viewed location by each co-actor. However, the present findings also indicate that potential benefits in time may be accompanied by costs in accuracy, and depending on the application, a higher importance may be placed on performance accuracy than performance speed (e.g., when reading a medical image).
Open practices statement
All data of the present experiment are available in the following repository: https://osf.io/e9xpb/?view_only=f07de98b22d74a7baa29905e5c0f2fff. The study was not preregistered. A preprint of this manuscript is available in the following preprint repository: https://doi.org/10.31234/osf.io/894zt
References
Alnæs, D., Sneve, M.H., Espeseth, T., Endestad, T., van de Pavert, S. H. P., & Laeng, B. (2014). Pupil size signals mental effort deployed during multiple object tracking and predicts brain activity in the dorsal attention network and the locus coeruleus. Journal of Vision, 14(4), 1–1.
Bahrami, B., Olsen, K., Latham, P. E., Roepstorff, A., Rees, G., & Frith, C. D. (2010). Optimally interacting minds. Science, 329(5995), 1081–1085.
Bartoń, K. (2018). MuMIn: Multi-model inference. R package version 1.42.1.
Belletier, C., Normand, A., & Huguet, P. (2019). Social-facilitation-and-impairment effects: From motivation to cognition and the social brain. Current Directions in Psychological Science, 28, 1–6.
Brennan, A. A., & Enns, J. T. (2015a). What’s in a friendship? partner visibility supports cognitive collaboration between friends. PLoS ONE, 10(11), e0143469.
Brennan, A. A., & Enns, J. T. (2015b). When two heads are better than one: Interactive versus independent benefits of collaborative cognition. Psychonomic Bulletin & Review, 22(4), 1076– 1082.
Brennan, S. E., Chen, X., Dickinson, C. A., Neider, M. B., & Zelinsky, G. J. (2008). Coordinating cognition: The costs and benefits of shared gaze during collaborative search. Cognition, 106(3), 1465–1477.
Czeszumski, A., Ehinger, B. V., Wahn, B., & König, P. (2019). The social situation affects how we process feedback about our actions. Frontiers in Psychology, 10, 361.
Davis, M. H. (1983). Measuring individual differences in empathy: Evidence for a multidimensional approach. Journal of Personality and Social Psychology, 44(1), 113.
Frith, C. D., & Frith, U. (2012). Mechanisms of social cognition. Annual Review of Psychology, 63, 287–313.
Johnson, P. C. (2014). Extension of Nakagawa & Schielzeth’s R2GLMM to random slopes models. Methods in Ecology and Evolution, 5(9), 944–946.
Knoblich, G., & Jordan, J. S. (2003). Action coordination in groups and individuals: Learning anticipatory control. Journal of Experimental Psychology: Learning, Memory, and Cognition, 29(5), 1006–1016.
Mahmoodi, A., Bang, D., Olsen, K., Zhao, Y. A., Shi, Z., Broberg, K., ..., et al. (2015). Equality bias impairs collective decision-making across cultures. Proceedings of the National Academy of Sciences, 112(12), 3835–3840.
Nakagawa, S., & Schielzeth, H. (2013). A general and simple method for obtaining r2 from generalized linear mixed-effects models. Methods in Ecology and Evolution, 4(2), 133–142.
Neider, M. B., Chen, X., Dickinson, C. A., Brennan, S. E., & Zelinsky, G. J. (2010). Coordinating spatial referencing using shared gaze. Psychonomic Bulletin & Review, 17(5), 718–724.
Papoutsaki, A., Sangkloy, P., Laskey, J., Daskalova, N., Huang, J., & Hays, J. (2016). Webgazer: Scalable webcam eye tracking using user interactions. In Proceedings of the 25th international joint conference on artificial intelligence-IJCAI 2016.
Rajaram, S., & Pereira-Pasarin, L. P. (2010). Collaborative memory: Cognitive research and theory. Perspectives on psychological science, 5(6), 649–663.
Sebanz, N., Bekkering, H., & Knoblich, G. (2006). Joint action: bodies and minds moving together. Trends in Cognitive Sciences, 10(2), 70–76.
Shinners, P. (2011). Pygame. http://pygame.org/.
Sternshein, H., Agam, Y., & Sekuler, R. (2011). EEG correlates of attentional load during multiple object tracking. PLoS ONE, 6(7), e22660.
Szymanski, C., Pesquita, A., Brennan, A. A., Perdikis, D., Enns, J. T., Brick, T. R., ..., Lindenberger, U. (2017). Teams on the same wavelength perform better: Inter-brain phase synchronization constitutes a neural substrate for social facilitation. NeuroImage, 152, 425–436.
Townsend, J. T., & Ashby, F. G. (1978). Methods of modeling capacity in simple processing systems. Cognitive theory, 3, 200–239.
Townsend, J. T., & Ashby, F. G (1983). Stochastic modeling of elementary psychological processes. CUP Archive.
Vesper, C., Abramova, E., Bütepage, J., Ciardo, F., Crossey, B., Effenberg, A., ..., Wahn, B. (2017). Joint action: Mental representations, shared information and general mechanisms for coordinating with others. Frontiers in Psychology, 7, 2039.
Wahn, B., Czeszumski, A., & König, P. (2018a). Performance similarities predict collective benefits in dyadic and triadic joint visual search. PLoS ONE, 13(1), e0191179.
Wahn, B., Ferris, D. P., Hairston, W. D., & König, P. (2016a). Pupil sizes scale with attentional load and task experience in a multiple object tracking task. PLoS ONE, 11(12), e0168087.
Wahn, B., Karlinsky, A., Schmitz, L., & König, P. (2018b). Let’s move it together: a review of group benefits in joint object control. Frontiers in Psychology, 9, 918.
Wahn, B., Kingstone, A., & König, P. (2017). Two trackers are better than one: Information about the co-actor’s actions and performance scores contribute to the collective benefit in a joint visuospatial task. Frontiers in Psychology, 8, 669.
Wahn, B., Kingstone, A., & König, P. (2018c). Group benefits in joint perceptual tasks–a review. Annals of the New York Academy of Sciences, 1426(1), 166–178.
Wahn, B., Schmitz, L., König, P., & Knoblich, G. (2016b). Benefiting from being alike: Interindividual skill differences predict collective benefit in joint object control. In Proceedings of the 38th annual conference of the Cognitive Science Society (pp. 2747–2752).
Wahn, B., Schwandt, J., Krüger, M., Crafa, D., Nunnendorf, V., & König, P. (2016c). Multisensory teamwork: Using a tactile or an auditory display to exchange gaze information improves performance in joint visual search. Ergonomics, 59, 781–795.
Acknowledgements
We acknowledge the support of a DFG fellowship (WA 4153/2-1) awarded to BW and the support by H2020 – H2020-FETPROACT-2014 641321 – socSMCs (for AC & PK).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Wahn, B., Czeszumski, A., Labusch, M. et al. Dyadic and triadic search: Benefits, costs, and predictors of group performance. Atten Percept Psychophys 82, 2415–2433 (2020). https://doi.org/10.3758/s13414-019-01915-0
Published:
Issue Date:
DOI: https://doi.org/10.3758/s13414-019-01915-0