Abstract
Zylberberg et al. [Zylberberg, Barttfeld, & Sigman (Frontiers in Integrative Neuroscience, 6; 79, 2012), Frontiers in Integrative Neuroscience 6:79] found that confidence decisions, but not perceptual decisions, are insensitive to evidence against a selected perceptual choice. We present a signal detection theoretic model to formalize this insight, which gave rise to a counter-intuitive empirical prediction: that depending on the observer’s perceptual choice, increasing task performance can be associated with decreasing metacognitive sensitivity (i.e., the trial-by-trial correspondence between confidence and accuracy). The model also provides an explanation as to why metacognitive sensitivity tends to be less than optimal in actual subjects. These predictions were confirmed robustly in a psychophysics experiment. In a second experiment we found that, in at least some subjects, the effects were replicated even under performance feedback designed to encourage optimal behavior. However, some subjects did show improvement under feedback, suggesting the tendency to ignore evidence against a selected perceptual choice may be a heuristic adopted by the perceptual decision-making system, rather than reflecting inherent biological limitations. We present a Bayesian modeling framework that explains why this heuristic strategy may be advantageous in real-world contexts.
Similar content being viewed by others
Introduction
Human subjects are capable of conscious introspection upon their own perceptual processes, an ability sometimes referred to as metacognition (Charles, Van Opstal, Marti, & Dehaene, 2013; Fleming, Dolan, & Frith, 2012; Goldberg, Harel, & Malach, 2006). In sensory psychophysics experiments, this ability is reflected in the fact that subjects’ confidence ratings correlate meaningfully with the likelihood of accurate decisions (Fleming, Huijgen, & Dolan, 2012; Fleming, Weil, Nagy, Dolan, & Rees, 2010). In traditional psychophysics models (Green & Swets, 1966; King & Dehaene, 2014; Macmillan & Creelman, 2004), subjects are assumed to rate their confidence based on the same internal sensory evidence underlying perceptual decisions; this theoretical view is adopted in recent animal studies (Kepecs, Uchida, Zariwala, & Mainen, 2008), and supported by the finding that there are single neurons whose firing rate reflects both confidence and perceptual decision (Kiani & Shadlen, 2009).
Thus, an optimal strategy for both making a perceptual decision and rating confidence in that decision ought to weigh evidence in favor of the chosen alternative (“response-congruent” evidence) and evidence against the chosen alternative (i.e., in favor of the unchosen alternative; “response-incongruent” evidence) equally. However, at least one recent behavioral study (Zylberberg, Barttfeld, & Sigman, 2012) suggests a different view, whereby the level of confidence is driven mainly by the response-congruent evidence, and is largely insensitive to the level of response-incongruent evidence. The perceptual decision itself, however, is driven equally by response-congruent and response-incongruent evidence. For instance, consider a “left or right” discrimination task, in which the observer is asked to decide whether a target is presented in the left or right location (e.g., Fig. 1). According to this strategy, when subjects decide the target was presented on the left (for example), they make the decision based on how much perceptual evidence there is for the target having been presented on the left, relative to how much perceptual evidence there is for the target having been presented on the right. Their confidence, on the other hand, is driven mainly by the strength of evidence in favor of the side they chose (e.g., evidence that the target was on the left), but is relatively insensitive to however much evidence exists for the other location (e.g., evidence that the target was on the right).
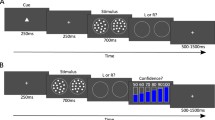
Experimental design for Experiments 1 and 2. Participants performed a simple spatial two-alternative forced choice (2AFC) task. Two circular patches of visual noise were presented to the left and right of fixation. One of the patches contained an embedded sinusoidal grating. After stimulus presentation, participants provided a stimulus judgment (which side contained the grating?) and a confidence judgment (how confident are you that your response was correct?). When the grating was presented on one side of the screen, its contrast was constant throughout the experiment (S1 stimulus). When it was presented on the other side, it could take on one of five possible contrasts (S2 stimulus). Thus, the design manipulated S2 stimulus strength in the same way depicted in Fig. 3. Mapping of S1 and S2 stimuli to left and right sides of the screen was counterbalanced across participants. In Experiment 2, the confidence judgment was replaced by a point-wagering system in which participants won or lost the number of wagered points depending on task accuracy. In Experiment 2, participants also received performance feedback after every trial and after every block
If proven true, this dissociation between evidence used for perceptual decision versus confidence judgments may have considerable impact on our understanding of neural coding of probabilistic information—especially because such a strategy may seem suboptimal from a Bayesian standpoint, given that the response-incongruent evidence is just as relevant to the perceptual decision (Beck et al., 2008; Kepecs & Mainen, 2012; Kepecs et al., 2008; Ma, Beck, Latham, & Pouget, 2006; Vickers, 1979). In this paper, we set out to test a simple signal detection theoretic (SDT) model of confidence implementing this strategy of relying only on response-congruent evidence to rate confidence. We validated the model with one psychophysics study, and used a second study to demonstrate that, in at least some subjects, such apparent suboptimalities are resistant to correction through feedback and instructions. We discuss why an observer in the real world might rely on such an apparently suboptimal strategy to rate confidence, and provide a Bayesian framework to formalize this intuition.
Methods
Detection theoretic model in 2-dimensional representation space
Signal detection theory (SDT) provides a simple model for perceptual decisions in the context of ambiguous evidence. In the simplest case, the observer must decide whether a viewed stimulus belongs to one of two stimulus classes, S1 or S2. Typical SDT models suppose that repeated presentations of S1 and S2 are associated with Gaussian distributions of perceptual evidence, e, along a single internal response dimension that codes the degree of evidence in favor of an “S1” or “S2” response. SDT assumes that the observer sets a decision criterion, such that all evidence values above the criterion elicit an “S2” response while those below it elicit an “S1” response.
However, to independently manipulate the amount of response-congruent versus response-incongruent evidence, and thereby observe how these quantities contribute to both perceptual decisions and confidence judgments, a two-dimensional SDT model is required. This two-dimensional model is a straightforward generalization of the one-dimensional case (Fig. 2a): two internal response dimensions independently code the magnitude of evidence favoring an “S1” response and an “S2” response, respectively. On each trial, therefore, the observer sees not one evidence value representing the overall balance of S1 versus S2 evidence, but a pair of evidence values, which we will call e = (eS1, eS2). As in the one-dimensional case, we assume repeated presentations to be associated with Gaussian distributions, but this time as bivariate distributions of (eS1, eS2) pairs. These distributions are depicted as concentric circles in Fig. 2a. The optimal strategy is to respond “S1” whenever eS1 > eS2, which corresponds to setting a decision criterion in evidence space along the line eS1 – eS2 = 0. This strategy is optimal for the stimulus identification task in the sense that it maximizes the proportion of the observer’s responses that are correct. This optimal strategy is consistent with Zylberberg et al.’s (2012) finding that response-congruent and response-incongruent evidence contribute equally to perceptual decisions. We will call this the “Balance of Evidence” decision rule.
a The two-dimensional signal detection theory model of discrimination tasks. The observer decides whether evidence presented on a given trial belonged to some arbitrary stimulus class, S1 or S2. The observer’s perception can be summarized by a pair of numbers (eS1, eS2), representing the evidence in favor of each stimulus category, respectively. These pairs of numbers (eS1, eS2) are assumed to follow bivariate Gaussian distributions, depicted by concentric circles. The optimal response strategy is to respond “S1” if eS1 – eS2 > 0, and “S2” otherwise. The dotted line represents this criterion; the gray shaded region denotes regions in which the pair (eS1, eS2) will elicit an “S1” response. b Balance-of-Evidence (BE) rule for confidence rating. The optimal strategy is to rely on the same quantity used to make the decision, i.e., eS1 – eS2, which means confidence criteria will be placed along the S1 – S2 axis. Light-, medium-, and dark-shaded regions denote low, medium, and high confidence, respectively. c Response-Congruent-Evidence (RCE) rule for confidence rating. Confidence is rated only along the axis of the chosen response category, such that confidence in an “S1” response will be determined solely by the value of eS1 and will ignore the value of eS2. As before, light-, medium-, and dark-shaded regions denote low, medium, and high confidence, respectively
Confidence judgments
In order to rate confidence (e.g., “high” or “low”), the observer must rely on additional criteria or decision rules. The optimal way to rate confidence is to use the same Balance of Evidence rule used in the perceptual decision, i.e., the difference in magnitude between eS1 and eS2. For example, if an observer has chosen “S1”, she could use a rule for confidence rating such as “Reply high confidence if eS1 – eS2 > 1, otherwise reply low confidence.” This strategy corresponds to evaluating confidence along the S1 – S2 axis, parallel to the decision criterion (Fig. 2b).
The Balance of Evidence strategy is optimal for confidence rating in the sense that it maximizes the proportion of high confidence responses for correct trials (i.e., type 2 hit rate) for a given proportion of high confidence responses for incorrect trials (i.e., type 2 false alarm rate). The tradeoff in the proportion of high confidence responses for correct and incorrect responses can be represented with a type 2 ROC curve, which plots type 2 hit rate against type 2 false alarm rate. The area under the type 2 ROC curve (AUC) is an index of type 2 sensitivity, i.e., the efficacy with which confidence ratings distinguish correct from incorrect responses. According to SDT, an observer’s performance on the primary task places an upper bound on type 2 AUC (Galvin, Podd, Drga, & Whitmore, 2003; Maniscalco & Lau, 2012). The SDT measure of type 2 sensitivity, meta-d’, is defined such that if an observer’s type 2 ROC curve matches the theoretical type 2 ROC curve posited by SDT, then meta-d’ = d’ (Maniscalco & Lau, 2012, 2014). Thus, another way of framing the optimality of the Balance of Evidence rule for confidence rating is that, if an observer uses the Balance of Evidence rule to rate confidence, then meta-d’ = d’ (Fig. 4a). (It is worth noting that although SDT thus provides a framework for quantifying the optimality of confidence ratings, it may not be immediately transparent to human subjects in a pyschophysics task that they should actively attempt to optimize the correspondence between confidence ratings and accuracy on individual trials in this way, even though subjects generally exhibit metacognitive performance that is well above chance and reasonably close to the SDT-optimal level (e.g., Maniscalco & Lau, 2012, 2015). Thus, our notion of optimality for confidence ratings is intended to provide an account of the limits of metacognitive performance, not necessarily to provide an account of how subjects approach the confidence rating task. Even if a subject does not place confidence ratings with the explicit intention of achieving optimality in this way, her SDT-optimal level of metacognitive performance can still be calculated given her performance on the task, and her actual metacognitive performance can still be compared against the SDT-optimal value.)
In contrast, if confidence ratings depend only on response-congruent evidence, then only the axis of the chosen distribution matters. That is, if the observer has chosen “S1” then she will rate confidence only according to the magnitude of eS1, and ignore the magnitude of eS2. She might respond “high confidence” if eS1 > 1, for example. Thus, in SDT terms, the confidence criteria are placed perpendicular to the S1 and S2 axes, respectively (Fig. 2c). We will call this the “Response-Congruent Evidence” decision rule.
To quantitatively assess predictions for the Balance of Evidence and Response-Congruent Evidence decision rules, we ran simulations based on this SDT model. We held the mean of the S1 distribution constant while varying the mean eS2 value of the S2 distribution, and assessed the predicted task performance and metacognitive sensitivity separately for both rules. See Supplemental Material for details of model simulation.
Behavioral experiments
In order to empirically verify the patterns predicted by our model simulations, we conducted two behavioral experiments of a spatial two-alternative forced-choice (2AFC) visual discrimination task. Participants viewed two stimuli presented on either side of a fixation cross, judged which of the stimuli contained a Gabor patch (sinusoidal grating) target, and rated their confidence in their decisions on a scale of 1–4 (Fig. 1). To match our simulations, stimulus strength in one spatial location was held constant (S1 stimulus) while stimulus strength in the other spatial location was varied across five possible values (S2 stimulus). In Experiment 1, we evaluated whether the Balance of Evidence or Response-Congruent Evidence rules better fit human behavioral response patterns. In Experiment 2, we examined whether the pattern of responses can be altered through performance feedback and task strategy manipulations (post-decisional wagering rather than confidence judgments).
Experiment 1
Participants
Three Columbia University students and two high school students participated in four experimental sessions each over four separate days. All participants gave informed consent and were paid US $10 for approximately 1 h of participation per session, and a US $5 bonus for completing all four experimental sessions. Procedures for both experiments were approved by the Columbia University’s Committee for the Protection of Human Subjects.
Data from one Columbia University participant was omitted from data analysis in Experiment 1. For this participant, d’ across the five levels of S2 stimulus strength ranged between approximately 0.2 and 0.6 in sessions 1–3 (near chance), and ranged between 3.4 and 3.8 in session 4 (near ceiling). Results of the analysis do not substantively change if data from the omitted participant is included.
Stimuli and procedures
Participants were seated in a dimmed room 60 cm away from a computer monitor. Stimuli were generated using Psychophysics Toolbox (Brainard, 1997; Pelli, 1997) in MATLAB (MathWorks, Natick, MA) and were shown on an iMac monitor (LCD, 24 inches monitor size, 1920 × 1200 pixel resolution, 60 Hz refresh rate).
Each stimulus was a circle (3° diameter) consisting of randomly generated visual noise. The target stimulus contained a randomly oriented sinusoidal grating (two cycles per degree) embedded in the visual noise, while the non-target contained noise only. On every trial, two stimuli—a target and a non-target—were presented simultaneously at ±4° to the left and right of fixation (Fig. 1) for 33 ms on a gray background. After stimulus presentation, participants provided a two-alternative forced-choice (2AFC) judgment of whether the left or the right stimulus contained a grating. Following stimulus classification, participants rated their confidence in the accuracy of their response on a scale of 1 through 4. Participants were encouraged to use the entire confidence scale. If the confidence rating was not registered within 5 s of stimulus offset, the next trial commenced automatically. (Such trials were omitted from all analyses.) There was a 1-s interval between the entry of confidence rating and the presentation of the next stimulus. Participants were instructed to maintain fixation on a small crosshair (0.35° wide) displayed in the center of the screen for the duration of each trial.
At the start of each experimental session, participants completed two practice blocks (28 trials each) and 1 calibration block (120 trials). In the calibration block, the detectability of the grating in noise was adjusted continuously between trials using the QUEST threshold estimation procedure (Watson & Pelli, 1983). Target stimuli were defined as the sum of a grating with Michelson contrast Cgrating and a patch of visual noise with Michelson contrast Cnoise. The total contrast of the target stimulus, Ctarget = Cgrating + Cnoise, was set to 0.9. The non-target stimulus containing only noise was also set to a Michelson contrast of 0.9. The QUEST procedure was used to estimate the ratio of the grating contrast to the noise contrast, Rgrating = Cgrating / Cnoise, which yielded 70 % correct performance in the 2AFC task. Three independent threshold estimates of Rgrating were acquired, with 40 randomly ordered trials contributing to each, and the median estimate of these, R* grating, was used to create stimuli for the main experiment.
Crucially, in the main experiment, the contrast of the grating presented on one side of the screen was constant, whereas the contrast of the grating presented on the other side could take on one of five possible values. We shall refer to the stimulus sequence containing the constant grating contrast “S1” and the stimulus sequence containing the variable grating contrast “S2”. The value of Rgrating for S1 was set to R* grating. The possible values of Rgrating for S2 were acquired by multiplying the value of R* grating by weights of 0.5, 0.75, 1, 1.25, and 1.5.
The main experiment in each experimental session (1000 trials) consisted of 10 blocks of 100 trials each, with a self-terminated rest period of up to a minute between blocks. S1 and S2 stimuli were equally likely and distributed randomly across trials. For S2 stimuli, each of the five possible values of Rgrating were equally likely and were distributed randomly across S2 presentations. Thus, each participant’s data included 2000 S1 trials and 400 S2 trials for each of the five levels of S2 stimulus strength.
For each participant, the mapping of the constant-contrast S1 stimulus class to the configuration (target left, non-target right) or (non-target left, target right) was counterbalanced across participants. This mapping was consistent across experimental sessions for each participant.
Experiment 2
Participants
Four Columbia University students participated in four experimental sessions each. All participants gave informed consent and were paid US $10 for approximately 1 h of participation per session, and a US $5 bonus for completing all four experimental sessions. Procedures for both experiments were approved by the Columbia University’s Committee for the Protection of Human Subjects.
Stimuli and procedures
Experimental design was identical to Experiment 1, with the exceptions noted below. Additionally, participant 3 completed five experimental sessions rather than the four sessions completed by other participants.
In order to give metacognitive evaluations of stimulus classifications an objective goal and an incentive for accuracy, the confidence rating system of Experiment 1 was replaced by a wagering system in Experiment 2. Participants were informed that, after making the stimulus classification response, they could wager between 1 and 4 points on the accuracy of their response. If the response was correct, then they would win the amount of points they wagered, but if the response was incorrect, then they would lose the amount of points they wagered. For trials where the stimulus classification and wager were not entered within 5 s of stimulus offset, 10 points were lost. Points were added to a running tally. Participants were given the goal of maximizing the total number of points won in each experimental session. They were instructed that the optimal strategy for maximizing points would involve (1) maximizing the number of correct responses, (2) wagering points according to the estimated likelihood of the stimulus classification response being correct, and (3) appropriately using the entire wagering scale.
Note that these instructions were technically incorrect, since under the point system used here, the optimal strategy for maximizing points would be to place the highest possible wager whenever the estimated probability of being correct exceeds chance. Nonetheless, participants used all levels of the wagering scale rather than only placing the highest possible wagers, suggesting that they did not compute and employ the optimal point wagering strategy. Furthermore, participants’ metacognitive performance was improved overall relative to Experiment 1 (cf. Figs. 4b and 7), suggesting that participants did not ignore the point wagering system and performance feedback, but rather that these changes indeed assisted them in elevating their metacognitive performance. Thus, despite the technical flaws in implementation, the point wagering and feedback system used here seemed to have the intended effect of informing and motivating participants with regards to their metacognitive performance.
Participants were provided with performance feedback after every trial and after every block. For correct trials, immediately after the entry of the wager, a green “+X” was presented at fixation for 1 s, where X was the number of points wagered on that trial. Additionally, at the onset of the visual feedback, a high-pitched tone was played for 122 ms. For incorrect trials, a red “-X” was presented instead, and the tone was low-pitched. For trials in which the participant did not enter the wager within 5 s of stimulus offset, the text “TOO SLOW” was presented in red font at fixation for 2 s, and a “–10” was displayed underneath to indicate that the participant had lost 10 points due to not entering both responses within the time limit.
During the break period occurring after every block of 100 trials, participants saw a summary of their wagering performance, including the number of points earned in the previous block and the maximum number of points possible with an “optimal” (albeit unrealistic) wagering strategy (wagering 4 points for correct choices and 1 point for incorrect choices). Observers also saw a measure of wagering efficiency: points earned divided by maximum possible points. These metrics were also provided summarizing performance in the experiment so far.
Since we expected performance feedback after every trial to affect task performance, we also slightly changed the stimulus parameters. In the QUEST thresholding procedure, we set the target level of performance to 65 % correct, expecting that performance in the main experiment would improve due to perceptual learning facilitated by trial feedback. We also set the weights used to obtain Rgrating values for the S2 stimulus to values of .7, .85, 1, 1.15, and 1.3 rather than the values of .5, .75, 1, 1.25, and 1.5 used in Experiment 1 in order to reduce the likelihood of some experimental conditions yielding task performance near chance or ceiling.
Estimation of response-conditional meta-d’
For all trials where a subject responds “S1,” we may calculate type 2 false alarm rate (proportion of errors endorsed with high confidence), and type 2 hit rate (proportion of correct responses endorsed with high confidence) as follows:
where h is the cutoff value for what levels of confidence rating is considered high confidence. Here subjects could indicate four levels of confidence on each trial, so setting h = 2, 3, and 4 provides all possible ways of collapsing the 4-point confidence rating scale into a binary scale of low and high confidence. Each level of h creates a unique (type 2 FAR, type 2 HR) pair, and all three such pairs can be used to estimate a type 2 ROC curve (see, e.g., Fig. S2).
In the classical SDT model of perceptual task performance, the parameter d’ reflects perceptual sensitivity, and the parameter c reflects response bias (Macmillan & Creelman, 2004). Previous work has demonstrated that specification of d’ and c is already sufficient to determine the type 2 ROC curves (Galvin et al., 2003; Maniscalco & Lau, 2012). Thus, one way of characterizing a subject’s empirical type 2 (metacognitive) performance is to calculate what value of d’, in conjunction with the subject’s empirically observed response bias, would have given rise to that subject’s empirical type 2 ROC curve according to SDT. This value is called meta-d’. We estimated meta-d’ for “S1” responses by using a maximum likelihood estimation procedure to find the value of d’, in conjunction with the subject’s empirical response bias, that would give rise to a theoretically derived type 2 ROC curve for “S1” responses most closely resembling the corresponding empirical type 2 ROC curve. Meta-d’ for “S2” responses was estimated similarly. Please see Maniscalco & Lau (2014) for more in-depth discussion of the estimation procedure for response-conditional meta-d’.
Results
Model predictions
The Response-Congruent Evidence decision rule can lead to a strong dissociation between stimulus discrimination performance and metacognitive performance. Figure 3 depicts the graphical intuition for how this might occur. Figure 3a shows a situation in which stimulus S2 is relatively weak (i.e., the mean value of eS2 is relatively low), and Fig. 3b shows a relatively strong S2 stimulus (the mean value of eS2 is relatively high). As the mean value for eS2 increases, the value of eS1 needed to incorrectly categorize the stimulus as S1 (i.e., to yield eS1 – eS2 > 0) will also increase, meaning that incorrect “S1” responses are associated with increasingly higher eS1 values. If the observer judges confidence according to the Response-Congruent Evidence rule, these increasingly higher eS1 values for incorrect “S1” responses will be associated with increasingly higher confidence. Because the distribution of confidence ratings for correct “S1” responses will not change (as the S1 distribution remains stationary), this means that a rating of “high confidence” in an “S1” response will become less diagnostic of whether that response is correct or not. Critically, as this metacognitive sensitivity decreases with increasing eS2 mean, task performance (measured by the SDT measure d’) actually increases, since d’ is proportional to the distance between the S1 and S2 distributions. This dissociation is a surprising and counterintuitive prediction, since a positive correlation between task performance and metacognitive sensitivity is a very robust empirical phenomenon and is a direct theoretical consequence of SDT (Galvin et al., 2003; Maniscalco & Lau, 2012). Note that the same dissociation is not predicted if confidence is judged according to the Balance of Evidence rule.
a, b Decreasing metacognitive sensitivity with increasing task performance according to the RCE rule. The strength of the S2 stimulus varies, while the strength of the S1 stimulus is held constant. For clarity, we show only one confidence criterion, dividing the “S1” response region into “high” (dark gray) and “low” (light gray) confidence responses. We also depict more contour lines here than in Fig. 2 for the sake of illustration. a Shows a situation in which the magnitude of the S2 stimulus is relatively weak (reflected by the small mean value for eS2 in the S2 distribution relative to the mean value for eS1 in the S1 distribution), while b shows a relatively strong S2 stimulus. Discrimination task performance (indexed here as the Euclidean distance between the means of the evidence distributions for S1 and S2, relative to their common standard deviation) is higher in b than in a. However, metacognitive sensitivity for “S1” responses is superior in a. To see why, note that the fraction of correct “S1” responses endorsed with high confidence (proportion of the S1 distribution above the diagonal colored in dark gray) is the same in a and b, but the fraction of incorrect “S1” responses endorsed with high confidence (proportion of the S2 distribution above the diagonal colored in dark gray) is higher in b than in a. This means that in b, confidence rating for “S1” responses is less diagnostic of accuracy. Thus, the RCE rule predicts a dissociation between task performance and metacognitive sensitivity under these conditions
We simulated stimulus discrimination responses and confidence ratings for the Balance of Evidence and Response-Congruent Evidence decision rules (see Supplemental Material). We used these simulated behavioral responses to estimate SDT measures of perceptual and metacognitive performance (d’ and meta-d’; Fig. 4a; Maniscalco & Lau, 2012, 2014). This analysis showed evidence for a selective decline in metacognitive performance for “S1” responses as S2 stimulus strength increased under the Response-Congruent Evidence decision rule (Fig. 4a). (See Supplemental Material and Figures S1 & S2 for additional visualizations of model simulations; all analyses and model variants predicted similar trends.) The Balance of Evidence rule did not predict this dissociation.
a, b Model predictions and results of Experiment 1. a Our signal detection theoretic (SDT) simulation (see Methods and Supplemental Material) shows that the RCE predicts a dissociation between task performance (d’) and metacognitive efficiency (meta-d’), due to metacognitive assessments of confidence for “S1” responses (red) becoming less diagnostic of task performance as task performance increases. In contrast, the BE predicts that metacognitive sensitivity ought to only increase with increasing task performance. b Experiment 1 results demonstrate good qualitative match to the simulated predictions of the RCE rule but not the BE rule. Error bars represent within-subject standard errors (Morey 2008)
Behavioral results
For each participant, trials from each level of S2 stimulus strength were combined across the multiple experimental sessions (see Methods) before performing SDT analysis. SDT analysis involved calculating 2AFC performance via the SDT measure d’, and evaluating metacognitive sensitivity through the measure meta-d’ (Maniscalco & Lau, 2012). Meta-d’ measures metacognitive sensitivity such that, if confidence ratings follow their expected patterns under SDT, meta-d’ = d’. SDT analysis was conducted separately for each level of S2 stimulus strength, yielding five values for d’ and meta-d’. For each level of S2 stimulus strength we also calculated response-specific meta-d’ separately for trials on which the participant responded “S1” or “S2” (Maniscalco & Lau, 2014). See Methods and Maniscalco & Lau (2014) for more details on estimation of response-specific meta-d’.
Experiment 1
Figure 4b shows a plot of the average across-subject values of overall and response-specific meta-d’ as a function of d’. As predicted by the Response-Congruent Evidence but not the Balance of Evidence decision rule, meta-d’ for “S2” responses increased with increasing d’, whereas meta-d’ for “S1” responses decreased.
We analyzed this effect statistically with a 5 (S2 stimulus strength) × 2 (response type: “S1” or “S2”) repeated measures ANOVA on meta-d’. Since there were an insufficient number of degrees of freedom to perform Mauchly’s Test of Sphericity, the Greenhouse-Geisser correction was used for all statistical tests (Girden, 1992). The ANOVA revealed a significant interaction between S2 stimulus strength and response type [Greenhouse-Geisser corrected F(2.287, 6.861) = 25.50, P = .001], verifying that the relationship between meta-d’ and S2 stimulus strength depends on response type.
We also performed across-session analyses of the individual participant data by computing d’ and meta-d’ values for every level of S2 stimulus strength within every experimental session. Each participant had four experimental sessions, each with 500 S1 trials and 100 S2 trials for each of the five levels of S2 stimulus strength. For participant 4, data from one session were omitted due to abnormally high meta-d’ values (>5) in two data cells, likely an artifact due to low trial counts. We treated data from each experimental session as an independent set of observations and performed a 5 (S2 stimulus strength) × 2 (response type: “S1” or “S2”) repeated measures ANOVA on meta-d’ separately for each participant.
Qualitatively, all four individual participants exhibited the dissociation whereby meta-d’ for “S1” responses decreased even as meta-d’ for “S2” responses increased (Fig. 5), demonstrating reliance on the Response-Congruent Evidence rule. The Greenhouse-Geisser corrected ANOVA analysis of the S2 stimulus strength x response type interaction for individual participants yielded results of F(1.417, 4.250) = 10.92, P = .024 for participant 1; F(1.751, 5.252) = 14.01, P = .009 for participant 2; F(1.495, 4.486) = 4.25, P = .096 for participant 3; and F(1.670, 3.340) = 7.846, P = .056 for participant 4.
Data for individual participants in Experiment 1. By treating individual experimental sessions as independent observations, meta-d’ curves were analyzed for each individual participant. One experimental session from Participant 4 was omitted due to noisy data. All participants displayed patterns consistent with the predictions of the RCE decision rule. Error bars represent within-subject standard errors (Morey 2008)
Experiment 2
Experiment 1 indicated that participants use the Response-Congruent Evidence rule for rating confidence. With Experiment 2, we wanted to encourage participants to use both response-congruent and response-incongruent evidence in their confidence judgments. We replaced the confidence-rating task with a post-decisional wagering task, and provided performance feedback on both the 2AFC and Type 2 choices.
Analysis procedures for Experiment 2 were identical to those used for individual participants in Experiment 1. As with Experiment 1, since there were an insufficient number of degrees of freedom to perform Mauchly’s Test of Sphericity in all ANOVAs performed, the Greenhouse-Geisser correction was used for all statistical tests (Girden, 1992).
With the introduction of the wagering system and copious performance feedback, two participants were able to update their strategies to reflect using both response-congruent and response-incongruent information. Qualitatively, Participants 1 and 4 showed no evidence of cross-over effect for the response-conditional meta-d’ curves, whereas Participants 2 and 3 did seem to exhibit this pattern, although the effect is visually less clear for Participant 3 (Fig. 6). So, as before, we performed across-session analyses on the data of individual participants. For Participant 4, data from two sessions were omitted due to abnormally high meta-d’ values (>6) in three data cells, likely an artifact due to low trial counts. We treated data from each experimental session as an independent set of observations and performed a 5 (S2 stimulus strength) × 2 (response type: “S1” or “S2”) repeated measures ANOVA on meta-d’ separately for each participant. For Participants 1 and 4, the S2 stimulus strength x response type interaction was not significant [Greenhouse-Geisser corrected F(1.861, 5.583) = 0.969, P = 0.4 for participant 1; F(1, 1) = 0.68, P = 0.6 for participant 4], consistent with the interpretation that these two participants had updated their response strategies to rely more on a Balance of Evidence kind of rule (Fig. 6). [For participant 4, the interaction was still not significant when all 4 sessions were included in the analysis; F(1.317, 3.95) = 0.174, P = 0.8.] However, for Participants 2 and 3, the interaction was still significant [Greenhouse-Geisser corrected F(1.425, 4.275) = 15.72, P = .012 for participant 2; F(2.533, 10.132) = 10.44, P = .002 for participant 3] (Fig. 6), suggesting that not all observers are able to update their metacognitive strategies with the provision of performance feedback and a more incentivized and “objective” system for evaluating task performance.
Data for individual participants for Experiment 2. Although Participants 1 and 4 updated their response strategies to display patterns more similar to those predicted by the BE rule, Participants 2 and 3 displayed patterns qualitatively similar to the predictions of the RCE decision rule. Error bars represent within-subject standard errors (Morey 2008)
Statistical comparison of experiments 1 and 2
To facilitate comparison to Experiment 1, we also assessed whether the average relationship across all participants in Experiment 2 between d’ and response-specific meta-d’ resembled the pattern predicted by the Balance of Evidence decision rule, rather than that predicted by the Response-Congruent Evidence decision rule. Averaged across participants, meta-d’ for “S1” responses now increased, rather than decreased, with increases in S2 stimulus strength. A 5 (S2 stimulus strength) × 2 (response type: “S1” or “S2”) repeated measures ANOVA on meta-d’ revealed that the S2 stimulus strength x response type interaction was no longer significant at the group level [Greenhouse-Geisser corrected F(1.3, 3.901) = 3.70, P = .13] (Fig. 7).
Results of Experiment 2 pooled across all participants, regardless of decision strategy. In contrast to the results of Experiment 1, the response-conditional meta-d’ curves in the Experiment 2 averaged data more closely followed the predicted patterns of the BE decision rule, rather than the RCE rule. Meta-d’ increased for both “S1” and “S2” responses as d’ increased, and both meta-d’ curves closely tracked SDT expectation. Error bars represent within-subject standard errors (Morey 2008)
Qualitatively, the plots in Figs. 4b and 5 suggest that Experiment 1 yielded a cross-over of the response-specific meta-d’ curves, whereas Fig. 6 suggests that task manipulations in Experiment 2 partially remediated this effect for some participants but not others. Separate statistical analysis of the two experiments is consistent with this interpretation: overall, there was a significant S2 stimulus strength x response type interaction in Experiment 1 (P = .001) but not in Experiment 2 (P = .13).
In order to directly assess whether these across-experiment differences were themselves statistically significant, we used all participants from Experiment 2 and performed a 5 (S2 stimulus strength) × 2 (response type: “S1” or “S2”) × 2 (experiment) repeated measures ANOVA, with experiment as a between-subject factor. Mauchly’s Test of Sphericity was not significant for S2 stimulus strength or the S2 stimulus strength x response type interaction (ps > .6), and so all subsequent tests assume sphericity.
The three-way interaction between S2 stimulus strength, response type, and experiment was significant [F(4, 24) = 4.75, P = .006), verifying that the experimental manipulations in Experiment 2 had a statistically significant effect upon the cross-over effect for the response-specific meta-d’ curves.
We also observed a marginal main effect of experiment on meta-d’ [F(1, 6) = 4.05, P = .09]. This effect can be observed by noting that in Figs. 4b and 7, although a similar range of d’ values is covered, meta-d’ is higher (closer to the dashed line indicating meta-d’ = d’) for Experiment 2. In fact, whereas meta-d’ is suboptimal with respect to SDT and Bayesian expectations in Experiment 1 (i.e., both meta-d’ curves fall below the dashed line), averaged meta-d’ achieves SDT expectation in Experiment 2 (i.e., both meta-d’ curves overlap the dashed line). Thus, the manipulations of Experiment 2 also had the effect of increasing overall metacognitive sensitivity to the level of optimality posited by SDT (meta-d’ = d’).
Dynamics of the change in decision rule in experiment 2
One final question concerns how the decision rule used for point wagering in Experiment 2 evolved over time. If participants gradually learned to update their decision rule over time as a function of performance feedback, then we might expect to see that the S2 stimulus strength x response type interaction changes as a function of time. To test this possibility, we conducted a 5 (S2 stimulus strength) × 2 (response type: “S1” or “S2”) × 4 (session number) repeated measures ANOVA across the four participants. If decision rule evolved gradually over experimental sessions, then we would expect to see that the S2 stimulus strength x response type interaction is significantly modulated by session number. However, the Greenhouse-Geisser corrected analysis of the three-way interaction of S2 stimulus strength x response type x session number was not significant [F(1.533, 4.598) = 1.21, P = 0.4)]. In order to conduct this analysis, we included all four sessions from participant 4, even though two of these sessions had been omitted from prior analyses; the three-way interaction was still not significant when omitting participant 4 from the analysis entirely [F(1.696, 3.392) = 0.81, P = 0.5]. Thus, we did not find evidence that the decision rule used for point wagering evolved gradually over sessions. However, the low temporal resolution afforded by this analysis due to the large number of trials required to estimate meta-d’ for each response type at each level of S2 stimulus strength, as well as the low number of participants entered into the analysis, limit the interpretability of this null finding.
Participants in Experiment 2 also exhibited superior overall levels of metacognitive performance than those in Experiment 1, so the dynamics of overall metacognitive performance in Experiment 2 may also be of interest. Thus, we investigated how meta-d’ / d’ changed over time. It is necessary to estimate meta-d’ / d’ separately for each level of S2 stimulus strength, since collapsing across S2 stimulus strength levels would lead a strong violation of the assumption of equality of variances in the S1 and S2 stimulus distributions (Maniscalco & Lau, 2014). Thus we computed the following analysis separately for each level of S2 stimulus strength.
We divided each experimental session into four quarters. For the first quarter, we extracted the first 125 (out of 500 total) trials where an S1 stimulus was presented, as well as the first 25 (out of 100 total) trials where an S2 stimulus of a particular stimulus strength was presented, and used these to compute meta-d’ / d’. We repeated this procedure for the remaining three quarters of the session. Computed across all four sessions, this yielded 16 time-ordered values for meta-d’ / d’ for each subject at each level of S2 stimulus strength. To increase robustness due to relatively low trial counts for S2 stimuli, we averaged meta-d’ / d’ across levels of S2 stimulus strength. We then submitted these data to a repeated measures ANOVA to assess the effect of time on meta-d’ / d’. However, the Greenhouse-Geisser corrected analysis did not reveal a significant effect of time [F(1.530, 4.589) = 1.49, P = 0.3)], and was also not significant when restricted to only the four quarters occurring within the first experimental session [F(1.164, 3.492) = 0.284, P = 0.7]. This is because the meta-d’ / d’ ratio was already around the SDT-optimal value of 1 in the earliest parts of the first experimental session; average meta-d’ / d’ for the four quarters of the first session were 1.07, 1.12, 1.06, and 0.92. Similar results were observed when omitting participant 4. Thus, we did not find evidence that overall metacognitive performance gradually improved over time, even within the first experimental session. However, similar caveats about the relatively low temporal resolution of this analysis, relatively low trial counts for each meta-d’ / d’ estimate, and low number of subjects entered into the ANOVA, limit the interpretability of this null finding.
Finally, we also investigated how overall meta-d’ / d’ changed across the 4 experimental sessions, using a similar methodology as described above. This analysis yielded a similar null finding [average meta-d’ / d’ = 0.97, 1.04, 1.16, 0.88; F(1.520, 4.561) = 3.06, P = 0.15].
Bayesian heuristic framework
Given the above results, it is natural to ask why a system might rely on such an apparently suboptimal strategy as the Response-Congruent Evidence decision rule. But this reliance on such a simple heuristic makes sense when we consider that an observer generally must engage in perceptual decision-making in a more natural environment—one in which the number of stimulus alternatives may not be apparent and the observer may not even be sure there is a stimulus present at all.
It is relatively straightforward to extend the simple two-dimensional SDT model described above to a Bayesian decision theoretic formulation (see e.g., King & Dehaene, 2014). Notably, with the most basic assumptions (described below), Bayesian and SDT formulations produce identical predictions. However, the Bayesian framework allows for potential extension beyond the simple simulation and experiments performed here, and so we provide a general treatment.
To make the decision about whether a given pair of evidence values e = (eS1, eS2) ought to be categorized as “S1” or “S2”, rather than compare the values of eS1 and eS2 directly, the Bayesian observer evaluates the posterior probability of each distribution given the evidence, i.e.,
where Si ~ N(μi, Σ), with μi defined as the evidence value associated with a prototypical example of each Si (i.e., the mean value for eSi) along the ith dimension and 0 otherwise. In the simple, two-stimulus case used in the current studies, we can define Σ as the 2 × 2 identity matrix, and p(S1) = p(S2) = 0.5. To extend this to the case of many stimulus alternatives, we can assume each stimulus alternative Si may accumulate evidence along n orthogonal dimensions, such that e = (eS1, eS2, …, eSn). Systematic correlations among evidence samples in favor of more than one stimulus choice could be accomplished through assigning non-zero values to covariances among the stimulus distributions assumed to be correlated, and a priori probabilities of the distributions could also be assigned as unequal when appropriate. Thus, the perceptual choice is accomplished via determining for each stimulus possibility
Unbiased observers will make their choice and respond “Sc” according to
As discussed above, if observers are optimal they should also rate their confidence [p(correct)] according to the same metric used in the perceptual choice, i.e., the probability of the chosen source Sc given the data available, i.e.,
And, as above, the observer can decide whether p(correct) indicates high or low confidence (or on any confidence scale) by using rules such as, “If p(correct) > 0.75, report high confidence.” Such a strategy would correspond to the Balance of Evidence decision rule.
However, in a situation in which the observer is deciding among many alternatives, the evidence in favor of the unchosen stimuli may be not only weak, but also extremely heterogeneous. Under such conditions it may not be reasonable to expect the observer to maintain representations of all the unchosen alternatives once a choice has been made. Additionally, in the real world the observer must also take into account the possibility that there is no stimulus present at all. Therefore, in evaluating confidence in a perceptual decision, a reasonable and efficient strategy may be to care only about the evidence in favor of the chosen stimulus, and to ignore any evidence in favor of the unchosen alternatives. That is, the observer will not evaluate the probability of being correct as the posterior probability of the chosen distribution as compared to the unchosen distribution(s), but instead as the posterior probability of the chosen distribution with respect to the possibility of no stimulus at all.
So we introduce another distribution about which the observer possesses some knowledge: the “nothing” or “pure noise” distribution N, such that N ~ N([0,0], Σ) and Σ is the 2 × 2 identitity matrix as above (although these choices for mean and variance/covariance can of course be relaxed at a later time). Since the observer only cares about evidence in favor of the chosen distribution, it discards any evidence in favor of unchosen distributions to form a new estimate of the evidence, ê, where ê takes the value eSc in the cth dimension (the chosen stimulus) and is 0 elsewhere. For example, in the two-alternative case, if the observer chooses S1 then ê = (eS1, 0). The observer can now determine confidence by calculating a new posterior probability,
This confidence level can then be evaluated according to a similar rule as above, e.g. “If p(correct) > 0.75, report high confidence.” This strategy corresponds to the Response-Congruent Evidence rule. In essence, the observer is evaluating the probability that the evidence it sees in favor of its choice actually came from the category it chose, relative to there being nothing present at all. In the real world, this strategy makes sense: things that are quite detectable are generally also quite discriminable, so the more evidence you have for the stimulus you chose relative to nothing at all, the more confident you ought to be in your decision about what it is.
We relied on the SDT framework described in the Methods section for our simulations to avoid complicated assumptions about elements in the Bayesian formulation, such as the exact form or location of the “nothing at all” distribution N, the a priori probability that the stimulus is present or not p(N), and the presence or a priori probability of more than two stimulus alternatives Si, etc. Note that by assuming the distributions S1, S2, and N are isometric bivariate Gaussian distributions with Σ = the 2 × 2 identity matrix and a flat prior across both stimulus distributions, this Bayesian formulation reduces to the simple SDT version used for the simulations. However, in providing this framework we demonstrate the extensibility of this line of thinking to situations beyond the popular “two equally probable, uncorrelated alternatives” paradigm employed in many psychophysics experiments.
Discussion
Here we provide evidence supporting the view that humans’ confidence ratings depend almost entirely on response-congruent evidence in favor of the selected choice, despite stimulus judgements depending on a balance of evidence both in favor of and against the chosen stimulus category (Zylberberg et al., 2012). We formulated and tested a simple SDT model, coupled with a Bayesian framework capable of extension to more realistic situations, to show that this strategy may be a useful heuristic that is computationally convenient. Our model also generated a novel and counterintuitive behavioral prediction—that we can increase the physical strength of a stimulus and yet impair the subject’s metacognition (Fig. 4a)—which we tested and confirmed in Experiment 1 (Fig. 4b).
This result not only replicates previous psychophysical results (Zylberberg et al., 2012), but is also compatible with the observation in other studies that confidence and accuracy can be dissociated under different experimental conditions (Lau & Passingham, 2006; Rahnev et al., 2011; Rahnev, Maniscalco, Luber, Lau, & Lisanby, 2012; Rounis, Maniscalco, Rothwell, Passingham, & Lau, 2010; Zylberberg, Roelfsema, & Sigman, 2014), e.g., under different levels of noise (Fetsch, Kiani, Newsome, & Shadlen, 2014; Rahnev et al., 2012; Zylberberg et al., 2014) or attentional conditions (Rahnev et al., 2011). This work is also congruent with previous observations that a change in confidence is often accompanied by a change in detection bias (Rahnev et al., 2011); the two are intimately linked (Ko & Lau, 2012). Thus, if subjects evaluate their confidence in perceptual decisions along the “wrong” dimension (of response-congruent evidence—or “detection” of the chosen stimulus—even when the task is explicitly discrimination), this could also explain why human metacognitive performance tends to be worse than ideal (Maniscalco & Lau, 2012, 2015; McCurdy et al., 2013). Compare with Fig. 4b, in which subjects’ overall meta-d’ significantly underperforms the SDT-optimal level of meta-d’ at all levels of task performance, as would be expected if subjects obey the Response-Congruent Evidence decision rule (cf. Fig. 4a).
To our knowledge, this is the first study to demonstrate an empirical dissociation between task performance and metacognitive sensitivity of the form represented in Fig. 4b. However, it should be noted that this dissociation depends on the unique experimental design used here, in which we parametrically alter the stimulus strength of S2 stimuli across trials while always using the same stimulus strength for S1 stimuli in a 2AFC design. We chose this unusual experimental design precisely because it provides a powerful way for discriminating between the Balance of Evidence and Response-Congruent Evidence decision rules. In most typical experiments investigating perceptual metacognition, the S1 and S2 stimulus in a 2AFC design would always be set to equivalent levels of stimulus strength, and such a design would not yield the dissociation discussed here. Thus, the dissociation is better thought of as a consequence of the Response-Congruent Evidence rule that can be observed in properly contrived experimental scenarios, rather than as a phenomenon that can be readily observed across many kinds of experimental designs. What may be a commonly occurring phenomenon is not the dissociation as such, but rather the Response-Congruent Evidence decision rule for confidence rating that generates it.
A more common signature of the Response-Congruent Evidence decision rule than the response-dependent dissociation demonstrated here may be an overall suboptimality in metacognitive performance. For instance, the third data point of the overall meta-d’ curve in Fig. 4b is a case where the S1 and S2 stimuli in the 2AFC task have equal stimulus strength (corresponding to a typical psychophysics experimental design) and meta-d’ < d’, consistent with previous empirical demonstrations that meta-d’ < d’ in similar 2AFC tasks (Maniscalco & Lau, 2012, 2015; McCurdy et al., 2013). However, in general, the finding that meta-d’ < d’ in and of itself is not sufficient grounds to infer that participants use the Response-Congruent Evidence rule for confidence rating, as other possible mechanisms may also explain such a finding. Thus, while usage of the Response-Congruent Evidence rule is a candidate explanation for findings that meta-d’ < d’, careful experimental design and analysis techniques are generally required to make specific inferences about the mechanisms underlying suboptimal metacognition in a given data set.
Previous electrophysiological studies in primates have suggested that the same neurons may code for evidence accumulation in a perceptual decision making task and confidence in the perceptual decision (Kiani & Shadlen, 2009). Such findings are not necessarily inconsistent with the possibility that perceptual decisions are based on a Balance of Evidence rule, whereas confidence judgments are based on a Response-Congruent Evidence rule. This is because Balance of Evidence and Response-Congruent Evidence quantities, while distinct, are correlated. For instance, consider low and high confidence “S2” responses for a subject who uses the Balance of Evidence rule for the perceptual task and the Response-Congruent Evidence rule for the confidence rating task. By definition, low and high confidence “S2” responses will be associated with low and high values of evidence in favor of responding “S2,” i.e., the quantity we have termed eS2 in the discussion of our SDT model above. Similarly, by definition, eS2 – eS1 > 0 for trials where the subject responded “S2.” If eS2 and eS1 are uncorrelated, then high confidence “S2” trials will tend to be associated not only with higher values of the response-congruent evidence eS2, but also with higher levels of the balance of evidence, eS2 – eS1. Similar considerations hold for “S1” responses. Thus, in this scenario, a researcher might discover that the balance of evidence eS2 – eS1 differs as a function of confidence and conclude that the balance of evidence is used to determine both perceptual response and confidence, even though confidence in this example is in fact determined by the correlated but distinct quantity of response-congruent evidence, eS2.
In Experiment 2 we attempted to remedy the demonstrated dissociation between performance and metacognitive sensitivity by providing feedback on task and metacognitive performance and using a wagering system in lieu of confidence ratings. As a result, two of our four observers demonstrated behavior suggesting they were using both response-congruent and response-incongruent evidence in their confidence ratings, but the other two failed to do so (Fig. 6). This suggests that the Response-Congruent Evidence decision rule may not be compulsory, but rather may be at least partially susceptible to intervention.
It is important to recognize that, in this study, the demonstration of a metacognitive dissociation and suboptimality in Experiment 1, and the partial remediation of these in Experiment 2, are concerned with metacognitive sensitivity rather than metacognitive response bias. Metacognitive sensitivity concerns how well confidence ratings discriminate between correct and incorrect responses, e.g., as operationalized by area under the type 2 ROC curve (see Methods and Fig. S2). Metacognitive response bias (including “miscalibration” and “overconfidence; Brenner, Koehler, Liberman, & Tversky, 1996; Fellner & Krügel, 2012), in contrast, concerns the criteria used for labeling a given level of certainty “low” or “high” confidence. Changes in confidence criteria change the location of an observer’s type 2 false alarm rate and type 2 hit rate on the type 2 ROC curve without changing area under the type 2 ROC curve (and thus, without changing meta-d’). Because the effects discussed in the present studies concern meta-d’, a measure of metacognitive sensitivity, they cannot be explained by recourse to decision criteria for confidence rating, but rather pertain to the quality and type of information used to rate confidence. For similar reasons, the remediation of suboptimal metacognitive sensitivity suggested in Experiment 2 is not readily comparable with previous empirical investigations of the effects of feedback on remediation of biases in decision making tasks (e.g., Morewedge et al., 2015), which are better characterized as pertaining to metacognitive response bias rather than metacognitive sensitivity.
Here we demonstrate that a point wagering system with performance feedback can assist some subjects in using the optimal Balance of Evidence rule rather than the suboptimal Response-Congruent Evidence rule for metacognitive evaluation of task performance. In principle, usage of the optimal decision rule for metacognitive judgments should generalize to any task requiring a similar binary classification of stimuli, although in practice it remains to be seen if learning to use the Balance of Evidence rule in one task would generalize to other tasks involving different task demands or sensory modalities. Additionally, the design of the present study does not allow us to infer the relative importance of the point wagering system and the provision of feedback for remediation of metacognitive performance, although it was also not the intention of the present study to tease these factors apart. Future studies focusing on ways to improve metacognitive performance should systematically investigate the relative importance of performance feedback, point wagering systems with various payoff matrices, and other similar factors for improving metacognition.
These results raise the question of why an ideal observer may use such apparently suboptimal strategies to generate decision confidence. To address this question, Zylberberg and colleagues (2012) fit their data to various models of dynamic perceptual decision-making that suppose noisy evidence is accumulated over time to a decision threshold. They found that the best-fitting model was a cross between a race model (Gold & Shadlen, 2007; Vickers, 1970) and a random walk model (Ratcliff & McKoon, 2008), such that sensory evidence for each response alternative is continuously accumulated in separate accumulators, with some “cross-talk” among them. They surmised that such partial “cross-talk” might be neurally implemented by slow lateral connections in attractor networks. However, if one were to view such low-level mechanisms as even partially “hard-wired”—and therefore unlikely to be susceptible to rapid top-down effects—it would be difficult to explain the results of our Experiment 2. Zylberberg et al. (2012) also speculated that higher-level metacognitive mechanisms may not have access to sensory-level evidence not related to the perceptual choice (i.e., negative evidence). This explanation also seems unlikely, since such processing capacity limits would likely be fixed properties of the cognitive system, and not susceptible to the manipulations we implemented in Experiment 2.
Might a drift diffusion model provide an alternative account of our findings that task performance and metacognitive sensitivity can dissociate? The dissociation between d’ and meta-d’ for “S1” responses occurs because, as S2 stimulus strength increases, average confidence for correct “S1” responses remains constant and yet average confidence for incorrect “S1” responses increases (Fig. 3, S1). Intuitively, as S2 stimulus strength increases, discrimination of the S2 stimulus becomes easier, and, accordingly, reaction time should decrease. If confidence and reaction time are inversely related, as postulated by the accumulator models of Zylberberg et al. (2012), then the drift diffusion model might also predict that confidence for incorrect “S1” responses increases with S2 stimulus strength, and thus account for the dissociation found in the present studies. (See Supplemental Material for an expanded discussion and description of diffusion model simulation and results.)
We conducted a drift diffusion model simulation and verified that this model yields decreasing reaction time for incorrect “S1” responses with increasing S2 stimulus strength (Fig. S4a). However, the empirical data do not support the crucial inverse relationship between confidence and reaction time that is required for the diffusion model to account for the dissociation. In particular, although average confidence for incorrect “S1” responses increased at the two highest levels of S2 stimulus strength in Experiment 1 (Fig. S3a), reaction time under these same conditions did not decrease but rather was constant (Fig. S4b). The inverse relationship between confidence and reaction time has also been questioned in other studies (Pleskac & Busemeyer, 2010; Koizumi, Maniscalco, & Lau, 2015). Thus, our SDT-based account has the advantage of being able to account for the dissociation between task performance and metacognitive sensitivity without having to assume an inverse relationship between confidence and reaction time, which appears to be an untenable assumption for this data set.
Importantly, a mechanistic model such as that offered by Zylberberg and colleagues (2012) does not address the question of why the brain may be wired to adopt such an apparently suboptimal way to generate confidence. On the other hand, although our proposed Bayesian heuristic framework is simple and not yet implementable with biologically realistic details, it provides justification for why such an apparently suboptimal heuristic strategy of confidence generation may be beneficial. Simply put, the strategy of rating confidence according only to response-congruent evidence makes sense in the broader context of perceptual decision-making in the real world, in which we must make decisions between not two but among many alternatives: once you decide that a visual stimulus is a cat (and not a dog, or rabbit, or monkey, or car, or table, etc.), you may not care how dog-like or table-like it is (or is not), but only how much evidence you have in favor of it being a cat. Indeed, in many cases you likely have very little information about what the stimulus is not, and it would be resource-intensive to attempt to maintain estimates of the quality of evidence in favor of all the possible unchosen alternatives. In this broader view, basing judgments of certainty in a perceptual decision on the strength of evidence in favor of the chosen stimulus category is both parsimonious and efficient: the more evidence you have in favor of the choice you made over there being nothing present at all, the more likely you are to be correct.
References
Beck, J. M., Ma, W. J., Kiani, R., Hanks, T., Churchland, A. K., Roitman, J., … Pouget, A. (2008). Probabilistic population codes for Bayesian decision making. Neuron, 60(6), 1142–1152.
Brainard, D. H. (1997). The psychophysics toolbox. Spatial Vision, 10(4), 433–436.
Brenner, L. A., Koehler, D. J., Liberman, V., & Tversky, A. (1996). Overconfidence in probability and frequency judgments: A critical examination. Organizational Behavior and Human Decision Processes, 65(3), 212–219. doi:10.1006/obhd.1996.0021
Charles, L., Van Opstal, F., Marti, S., & Dehaene, S. (2013). Distinct brain mechanisms for conscious versus subliminal error detection. NeuroImage, 73, 80–94. doi:10.1016/j.neuroimage.2013.01.054
Fellner, G., & Krügel, S. (2012). Judgmental overconfidence: Three measures, one bias? Journal of Economic Psychology, 33(1), 142–154. doi:10.1016/j.joep.2011.07.008
Fetsch, C. R., Kiani, R., Newsome, W. T., & Shadlen, M. N. (2014). Effects of cortical microstimulation on confidence in a perceptual decision. Neuron, 1–8. doi:10.1016/j.neuron.2014.07.011
Fleming, S. M., Dolan, R. J., & Frith, C. D. (2012a). Metacognition: Computation, biology and function. Philosophical Transactions of the Royal Society of London. Series B, Biological Sciences, 367(1594), 1280–1286. doi:10.1098/rstb.2012.0021
Fleming, S. M., Huijgen, J., & Dolan, R. J. (2012b). Prefrontal contributions to metacognition in perceptual decision making. The Journal of Neuroscience, 32(18), 6117–6125. doi:10.1523/JNEUROSCI.6489-11.2012
Fleming, S. M., Weil, R. S., Nagy, Z., Dolan, R., & Rees, G. (2010). Relating introspective accuracy to individual differences in brain structure. Science, 329(1541-1543).
Galvin, S. J., Podd, J. V., Drga, V., & Whitmore, J. (2003). Type 2 tasks in the theory of signal detectability: Discrimination between correct and incorrect decisions. Psychonomic Bulletin & Review, 10(4), 843–876.
Girden, E. R. (1992). ANOVA: Repeated Measures. London: SAGE.
Gold, J. I., & Shadlen, M. N. (2007). The neural basis of decision making. Annual Review of Neuroscience, 30, 535–574. doi:10.1146/annurev.neuro.29.051605.113038
Goldberg, I. I., Harel, M., & Malach, R. (2006). When the brain loses its self: Prefrontal inactivation during sensorimotor processing. Neuron, 50(2), 329–339. doi:10.1016/j.neuron.2006.03.015
Green, D. M., & Swets, J. A. (1966). Signal detection theory and psychophysics. New York: Wiley.
Kepecs, A., & Mainen, Z. F. (2012). A computational framework for the study of confidence in humans and animals. Philosophical Transactions of the Royal Society of London. Series B, Biological Sciences, 367(1594), 1322–1337. doi:10.1098/rstb.2012.0037
Kepecs, A., Uchida, N., Zariwala, H. A., & Mainen, Z. F. (2008). Neural correlates, computation and behavioural impact of decision confidence. Nature, 455(7210), 227–231. doi:10.1038/nature07200
Kiani, R., & Shadlen, M. N. (2009). Representation of confidence associated with a decision by neurons in the parietal cortex. Science, 324(5928), 759–764. doi:10.1126/science.1169405
King, J.-R., & Dehaene, S. (2014). A model of subjective report and objective discrimination as categorical decisions in a vast representational space. Philosophical Transactions of the Royal Society of London. Series B, Biological Sciences, 369(1641), 20130204. doi:10.1098/rstb.2013.0204
Ko, Y., & Lau, H. (2012). A detection theoretic explanation of blindsight suggests a link between conscious perception and metacognition. Philosophical Transactions of the Royal Society of London. Series B, Biological Sciences, 367(1594), 1401–1411. doi:10.1098/rstb.2011.0380
Lau, H. C., & Passingham, R. E. (2006). Relative blindsight in normal observers and the neural correlate of visual consciousness. Proceedings of the National Academy of Sciences of the United States of America, 103(49), 18763–18768. doi:10.1073/pnas.0607716103
Ma, W. J., Beck, J., Latham, P., & Pouget, A. (2006). Bayesian inference with probabilistic population codes. Nature Neuroscience, 9(11), 1432–1438.
Macmillan, N. A., & Creelman, C. D. (2004). Detection theory: A user’s guide. Mahwah: Taylor & Francis.
Maniscalco, B., & Lau, H. (2012). A signal detection theoretic approach for estimating metacognitive sensitivity from confidence ratings. Consciousness and Cognition, 21(1), 422–430.
Maniscalco, B., & Lau, H. (2014). Signal detection theory analysis of type 1 and type 2 data: Meta-d’, response-specific meta-d’, and the unequal variance SDT mode. In S. M. Fleming & C. D. Frith (Eds.), The Cognitive Neuroscience of Metacognition (pp. 25–66). Berlin: Springer. doi:10.1007/978-3-642-45190-4
Maniscalco, B., & Lau, H. (2015). Manipulation of working memory contents selectively impairs metacognitive sensitivity in a concurrent visual discrimination task. Neuroscience of Consciousness, 2015(1), niv002. doi:10.1093/nc/niv002
McCurdy, L. Y., Maniscalco, B., Metcalfe, J., Liu, K. Y., de Lange, F. P., & Lau, H. (2013). Anatomical coupling between distinct metacognitive systems for memory and visual perception. The Journal of Neuroscience : The Official Journal of the Society for Neuroscience, 33(5), 1897–1906. doi:10.1523/JNEUROSCI.1890-12.2013
Morewedge, C. K., Yoon, H., Scopelliti, I., Symborski, C. W., Korris, J. H., & Kassam, K. S. (2015). Debiasing decisions: Improved decision making with a single training intervention. Policy Insights from the Behavioral and Brain Sciences, 2(1), 129–140. doi:10.1177/2372732215600886
Morey, R. D. (2008). Confidence intervals from normalized data: A correction to Cousineau (2005). Tutorial in Quantitative Methods for Psychology, 4(2), 61–64.
Pelli, D. G. (1997). The VideoToolbox software for visual psychophysics: Transforming numbers into movies. Spatial Vision, 10(4), 437–442.
Pleskac, T. J., & Busemeyer, J. R. (2010). Two-stage dynamic signal detection: A theory of choice, decision time, and confidence. Psychological Review, 117(3), 864–901. doi:10.1037/a0019737
Rahnev, D., Maniscalco, B., Graves, T., Huang, E., De Lange, F. P., & Lau, H. (2011). Attention induces conservative subjective biases in visual perception. Nature Neuroscience, 14(12), 1513–1515. doi:10.1038/nn.2948
Rahnev, D., Maniscalco, B., Luber, B., Lau, H., & Lisanby, S. H. (2012). Direct injection of noise to the visual cortex decreases accuracy but increases decision confidence. Journal of Neurophysiology, 107(6), 1556–1563. doi:10.1152/jn.00985.2011
Ratcliff, R., & McKoon, G. (2008). The diffusion decision model: Theory and data for two-choice decision tasks. Neural Computation, 20(4), 873–922.
Rounis, E., Maniscalco, B., Rothwell, J. C., Passingham, R. E., & Lau, H. (2010). Theta-burst transcranial magnetic stimulation to the prefrontal cortex impairs metacognitive visual awareness. Cognitive Neuroscience, 1(3), 165–175. doi:10.1080/17588921003632529
Vickers, D. (1970). Evidence for an accumulator model of psychophysical discrimination. Ergonomics, 13(1), 37–58.
Vickers, D. (1979). Decision processes in visual perception. New York: Academic.
Watson, A., & Pelli, D. (1983). QUEST: A Bayesian adaptive psychometric method. Perception & Psychophysics, 33(2), 113–120.
Zylberberg, A., Barttfeld, P., & Sigman, M. (2012). The construction of confidence in a perceptual decision. Frontiers in Integrative Neuroscience, 6, 79. doi:10.3389/fnint.2012.00079
Zylberberg, A., Roelfsema, P. R., & Sigman, M. (2014). Variance misperception explains illusions of confidence in simple perceptual decisions. Consciousness and Cognition, 27C, 246–253. doi:10.1016/j.concog.2014.05.012
Acknowledgments
This work is partially supported by a grant from the Templeton Foundation (6-40689) and the National Institutes of Health (NIH R01 NS088628-01).
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
Below is the link to the electronic supplementary material.
ESM 1
(DOCX 1.65 mb)
Rights and permissions
About this article
Cite this article
Maniscalco, B., Peters, M.A.K. & Lau, H. Heuristic use of perceptual evidence leads to dissociation between performance and metacognitive sensitivity. Atten Percept Psychophys 78, 923–937 (2016). https://doi.org/10.3758/s13414-016-1059-x
Published:
Issue Date:
DOI: https://doi.org/10.3758/s13414-016-1059-x