Skip to main content
SpringerLink
Log in

Modeling the Distribution of Magnetization in a Rectangular Strip with an Axis of Easy Magnetization Perpendicular to the Plane

  • Published:
Bulletin of the Russian Academy of Sciences: Physics Aims and scope

Abstract

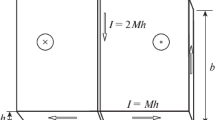
A theory is constructed for the ordering of magnetic domains in magnetic film materials in the presence of point dipole magnetic inhomogeneities. The distribution of magnetization is modeled for a rectangular strip with an axis of easy magnetization perpendicular to its plane in the presence of point dipole magnetic inhomogeneities. 3D modeling of the magnetic structure of the plate reveals the curvature of the domain boundary caused by the field of local magnetic inhomogeneity and along the thickness of the plate.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1.
Fig. 2.

Similar content being viewed by others

REFERENCES

  1. Landau, L.D. and Lifshitz, E.M., Course of Theoretical Physics, vol. 8: Electrodynamics of Continuous Media, Amsterdam: Elsevier, 1984.

    Google Scholar 

  2. Vonsovskii, S.V., Magnetizm. Magnitnye svoistva dia, para, ferro, antiferro i ferrimagnetikov (Magnetism. Magnetic Properties of Dia-, Para-, Ferro-, Antiferro-, and Ferrimagnetics), Moscow: Nauka, 1971.

  3. Kittel, Ch., Rev. Mod. Phys., 1949, vol. 21, p. 541.

    Article  ADS  Google Scholar 

  4. Eschenfelder, A.H., Magnetic Bubble Technology, New York: Springer, 1980.

    Book  Google Scholar 

  5. Akimov, M.L., Boltasova, Yu.V., and Polyakov, P.A., J. Commun. Technol. Electron., 2001, vol. 46, p. 469.

    Google Scholar 

  6. Akimov, M.L., Polyakov, P.A., and Usmanov, N.N., J. Exp. Theor. Phys., 2002, vol. 94, no. 2, p. 293.

    Article  ADS  Google Scholar 

  7. Akimov, M.L. and Polyakov, P.A., Moscow Univ. Phys. Bull. (Engl. Transl.), 2004, vol. 59, no. 2, p. 53.

    Google Scholar 

  8. Akimov, M.L., Vagin, D.V., Polyakov, O.P., et al., Bull. Russ. Acad. Sci.: Phys., 2007, vol. 71, no. 11, p. 1556.

    Article  Google Scholar 

  9. Akimov, M.L., Polyakov, P.A., Starokurov, Y.V., et al., Phys. B(Amsternam, Neth.), 2010, vol. 405, p. 2376.

    Article  ADS  Google Scholar 

  10. Akimov, M. L., Polyakov, P. A., Banishev, A. A., et al., Int. J. Mod. Phys. B, 2016, vol. 30, no. 12, 1650081.

    Article  ADS  Google Scholar 

  11. Akimov, M.L., Polyakov, P.A., and Rusakova, N.E., Int. J. Mod. Phys. B, 2018, vol. 32, no. 1, 1750272.

    Article  ADS  Google Scholar 

  12. Akimov, M.L., Polyakov, P.A., Banishev, A.A., et al., Int. J. Mod. Phys. B, 2019, vol. 33, no. 14, 1950142.

    Article  ADS  Google Scholar 

  13. Akimov, M.L. and Polyakov, P.A., Bull. Russ. Acad. Sci.: Phys., 2018, vol. 82, no. 8, p. 968.

    Article  Google Scholar 

  14. Bateman, H. and Erdélyi, A., Tables of Integral Transforms, New York: McGraw-Hill, 1954.

    Google Scholar 

  15. Handbook of Mathematical Functions: With Formulas, Graphs, and Mathematical Tables, Abramowitz, M. and Stegun, I.A., Eds., New York: Dover, 1965.

    Google Scholar 

Download references

Funding

This work was supported by the BASIS Foundation for the Development of Theoretical Physics and Mathematics.

Author information

Authors and Affiliations

  1. Department of Physics, Moscow State University, 119992, Moscow, Russia

    M. L. Akimov, P. A. Polyakov & V. S. Shevtsov

  2. Trapeznikov Institute of Control Sciences, Russian Academy of Sciences, 117997, Moscow, Russia

    V. S. Shevtsov

Authors
  1. M. L. Akimov
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. P. A. Polyakov
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. V. S. Shevtsov
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to M. L. Akimov.

Additional information

Translated by N. Petrov

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Akimov, M.L., Polyakov, P.A. & Shevtsov, V.S. Modeling the Distribution of Magnetization in a Rectangular Strip with an Axis of Easy Magnetization Perpendicular to the Plane. Bull. Russ. Acad. Sci. Phys. 84, 596–598 (2020). https://doi.org/10.3103/S1062873820050032

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.3103/S1062873820050032

Search

Navigation