Skip to main content
SpringerLink
Log in

Extraordinary spin momenta in birefringent structures

  • Published:
Optical Memory and Neural Networks Aims and scope Submit manuscript

Abstract

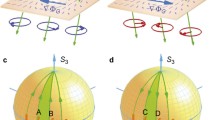
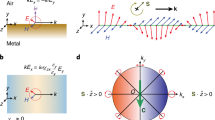
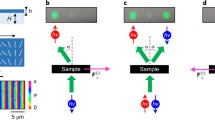
Mechanical action caused by the optical forces connected with the canonical momentum density associated with the local wave vector or classical spin angular momentum, the helicity dependent and the helicity independent forces determined by spin momenta of different nature open attractive prospects to use optical structures for manipulating with nanoobjects of different nature. The main finding of our study consists in demonstration of mechanical action of extraordinary transverse component of the spin angular momentum arising in an evanescent light wave due to the total internal reflection of linearly polarized probing beam with azimuth 45° at the interface ‘birefringent plate–air’.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Ohanian, H.C., What is spin?, Am. J. Phys., 1986, vol. 54, no. 6, pp. 500–505.

    Article  Google Scholar 

  2. Berry, M.V., Optical currents, J. Opt. A: Pure Appl. Opt., 2009, vol. 11, 094001, p. 12.

    Article  Google Scholar 

  3. Allen, L., Beijersbergen, M.W., Spreeuw, R.J., and Woerdman, J.P., Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes, Phys. Rev. A, 1992, vol. 45, 11, pp. 8185–8189.

    Article  Google Scholar 

  4. Allen, L. and Padgett, M.J., The Poynting vector in Laguerre–Gaussian beams and the interpretation of their angular momentum density, Opt. Commun., 2000, vol. 184, no. 1–4, pp. 67–71.

    Article  Google Scholar 

  5. Angelsky, O.V., Bekshaev, A.Ya., Maksimyak, P.P., Maksimyak, A.P., Mokhun, I.I., Hanson, S.G., Zenkova, C.Yu., and Tyurin, A.V., Circular motion of particles suspended in a Gaussian beam with circular polarization validates the spin part of the internal energy flow, Optics Express, 2012, vol. 20, no. 10, pp. 11351–11356.

    Article  Google Scholar 

  6. Angelsky, O.V., Bekshaev, A.Ya., Maksimyak, P.P., Maksimyak, A.P., Hanson, S.G., and Zenkova, C.Yu., Orbital rotation without orbital angular momentum: mechanical action of the spin part of the internal energy flow in light beams, Optics Express, 2012, vol. 20, no. 4, pp. 3563–3571.

    Article  Google Scholar 

  7. Polyanskii, V.K., Angelsky, O.V., and Polyanskii, P.V., Scattering-induced spectral changes as a singular optical effect, Optica Applicata, 2002, vol. 32, no. 4, pp. 843–848.

    Google Scholar 

  8. Angelsky, O., Besaha, R., Mokhun, A., Mokhun, I., Sopin, M., Soskin, M., and Vasnetsov, M., Singularities in vectoral fields, Proc. SPIE, 1999, vol. 3904, pp. 40–54.

    Article  Google Scholar 

  9. Angelsky, O.V., Bekshaev, A.Ya., Maksimyak, P.P., Maksimyak, A.P., Hanson, S.G., and Zenkova, C.Yu., Selfdiffraction of continuous laser radiation in a disperse medium with absorbing particles, Optics Express, 2013, vol. 21, no. 7, pp. 8922–8938.

    Article  Google Scholar 

  10. Angelsky, O.V., Ushenko, A.G., Ushenko, Ye.G., Tomka, Yu.Y., Polarization singularities of biological tissues images, J. Biomed. Opt., 2006, vol. 11, no. 5, p.9.

    Article  Google Scholar 

  11. Angelsky, O.V., Tomka, Yu.Y., Ushenko, A.G., Ushenko, Ye.G., Yermolenko, S.B., Ushenko, Yu.A., 2-D tomography of biotissue images in pre-clinic diagnostics of their pre-cancer states, Proc. SPIE, 2005, vol. 5972, pp. 158–162.

    Google Scholar 

  12. Zenkova, C.Yu., Yermolenko, S.B., Angelskaya, A.O., and Soltys, I.V., The polarization peculiarities of the correlation (intrinsic coherence) of optical fields, Opt. Mem. Neural Networks (Inform. Optics), 2011, vol. 20, no. 4, pp. 247–254.

    Article  Google Scholar 

  13. Zenkova, C.Yu., Gorsky, M.P., Soltys, I.V., and Angelsky, P.O., The investigation of the peculiarities of the motion of testing nanoobjects in the inhomogeneously-polarized optical field, Opt. Mem. Neural Networks (Inform. Optics), 2012, vol. 21, no. 1, pp. 34–44.

    Article  Google Scholar 

  14. Zenkova, C.Yu., Gorsky, M.P., and Ryabyj, P.A., Phase retrieval of speckle fields based on 2D Hilbert transform, Opt. Mem. Neural Networks (Inform. Optics), 2015, vol. 24, no. 4, pp. 303–308.

    Article  Google Scholar 

  15. Zenkova, C.Yu., Gorsky, M.P., Ryabiy, P.A., and Angelskaya, A.O., Additional approaches to solving the phase problem in optics, Appl. Opt., 2016, vol. 55, no. 12, pp. B78–B84.

    Article  Google Scholar 

  16. Zenkova, C.Yu., Gorsky, M.P., and Ryabyi, P.A., The phase problem solving by the use of optical correlation algorithm for reconstructing phase skeleton of complex optical fields, Proc. SPIE, 2015, vol. 9258, pp. 92582B–2–92582B–6.

    Google Scholar 

  17. Zenkova, C.Yu., Interconnection of polarization properties and coherence of optical fields, Appl. Opt., 2014, vol. 53, no. 10, pp. B43–B52.

    Article  Google Scholar 

  18. Zenkova, C.Yu., Gorsky, M.P., Soltys, I.V., and Angelsky, P.O., Use of motion peculiarities of test particles for estimating degree of coherence of optical fields, Ukr. J. Phys. Opt., 2012, vol. 13, no. 4, pp. 183–195.

    Article  Google Scholar 

  19. Zenkova, C.Yu., Kramar, V.M., and Kramar, N.K., Polarization optical bistability in layer crystals, Proc. SPT, 2006, pp. 254–257.

    Google Scholar 

  20. Angelsky, O.V., Zenkova, C.Yu., Gorsky, M.P., Soltys, I.V., and Angelsky, P.O., The use of new approaches to estimating the coherence properties of mutually orthogonal beams, Open Opt. J., 2013, vol. 7, pp. 5–2.

    Article  Google Scholar 

  21. Angelsky, O.V., Zenkova, C.Y., Gorsky, M.P., and Gorodynśka, N.V., Feasibility of estimating the degree of coherence of waves at the near field, Appl. Opt., 2009, vol. 48, no. 15, pp. 2784–2788.

    Article  Google Scholar 

  22. Antognozzi, M., Bermingham, C.R., Hoerber, H., Dennis, M.R., Bekshaev, A.Y., Harniman, R.L., Simpson, S., Senior, J., Bliokh, K.Y., and Nori, F., Direct measurements of the extraordinary optical momentum and transverse spin-dependent force using a nano-cantilever, Nat. Phys., 2016, p. 5.

    Google Scholar 

  23. Friese, M.E.J., Nieminen, T.A., Heckenberg, N.R., and Rubinsztein-Dunlop, H., Optical alignment and spinning of laser-trapped microscopic particles, Nature, 1998, vol. 394, pp. 348–350.

    Article  Google Scholar 

  24. Rockstuhl, C. and Herzig, H.P., Calculation of the torque on dielectric elliptical cylinders, J. Opt. Soc. Am. A, 2005, vol. 22, 1, pp. 109–116.

    Article  Google Scholar 

  25. Bekshaev, A.Ya., Angelsky, O.V., Sviridova, S.V., and Zenkova, C.Yu., Mechanical action of inhomogeneously polarized optical fields and detection of the internal energy flows, Adv. Opt. Technol., 2011, vol. 2011, p. 11.

    Article  Google Scholar 

  26. Bliokh, K.Y., Bekshaev, A.Y., and Nori, F., Extraordinary momentum and spin in evanescent waves, Nat. Commun., 2014, vol. 5, no. 3300.

    Article  Google Scholar 

  27. Hayata, A., Muellera, J.P.B., and Capassoa, F., Lateral chirality-sorting optical forces, PNAS Early Edition, 2015, p. 5.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Chernivtsi National University, Chernivtsi, Ukraine

    P. P. Maksimyak, A. P. Maksimyak & D. I. Ivanskyi

  2. RUDN University, Moscow, 117198, Russia

    T. V. Kiyashchuk

Authors
  1. P. P. Maksimyak
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. A. P. Maksimyak
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. D. I. Ivanskyi
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. T. V. Kiyashchuk
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to D. I. Ivanskyi.

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Maksimyak, P.P., Maksimyak, A.P., Ivanskyi, D.I. et al. Extraordinary spin momenta in birefringent structures. Opt. Mem. Neural Networks 26, 157–164 (2017). https://doi.org/10.3103/S1060992X17020059

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.3103/S1060992X17020059

Keywords

Search

Navigation