Abstract
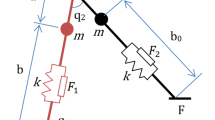
This paper investigates performance of two event-based controllers applied to an underactuated biped robot to stabilize its running gait in presence of uncertainties. Mechanism of the biped robot includes four links leg, one point mass at the hip, point feet, and three motors parallel to rotational springs. So it has one degree of underactuation during stance phase and three degrees of underactuation during flight phase. A discrete sliding mode controller (DSMC) in comparison with a discrete linear-quadratic regulator (DLQR) is examined in order to stabilize the fixed point of the corresponding Poincare map. Using numerical simulations, it is concluded that DSMC has a better performance regarding basin of attraction and convergence speed compared to DLQR, especially in presence of disturbances.
Similar content being viewed by others
References
Takenaka, T., The control system for the Honda humanoid robot, Age Ageing, 2006, vol. 35, pp. 1124–1126.
Ogura, Y., et al., Development of a new humanoid robot WABIAN-2, Proceedings 2006 IEEE International Conference on Robotics and Automation, ICRA, 2006.
Fixter, M., Fast trajectory generation using Bezier curves, Proceedings of the First Australian Undergraduate Students Computing Conference, 2003.
Cho, B.-K. and Oh, J.-H., Running pattern generation with a fixed point in a 2D planar biped, Int. J. Humanoid Rob., 2009, vol. 6, no. 2, pp. 241–264.
Manchester, I., et al., Stable dynamic walking over rough terrain: Theory and experiment, in ISRR 2009, Springer-Verlag, 2009.
Chevallereau, C., Westervelt, E., and Grizzle, J., Asymptotically stable running for a five-link, four-actuator, planar bipedal robot, Int. J. Rob. Res., 2005, vol. 24, no. 6, pp. 431–464.
Westervelt, E., Morris, B., and Farrell, K., Sample-based HZD control for robustness and slope invariance of planar passive bipedal gaits, in 14th Mediterranean IEEE Conference on Control and Automation, 2006.
Spong, M.W., Partial feedback linearization of underactuated mechanical systems, in Proceedings of the IEEE/RSJ/GI International Conference on Intelligent Robots and Systems, Advanced Robotic Systems and the Real World, 1994.
Kochuvila, S., Tripathi, S., and Sudarshan, T., Control of a compass gait biped robot based on partial feedback linearization, in Advances in Autonomous Robotics, Springer, 2012, pp. 117–127.
Tzafestas, S., Raibert, M., and Tzafestas, C., Robust sliding-mode control applied to a 5-link biped robot, J. Intell. Rob. Syst., 1996, vol. 15, no. 1, pp. 67–133.
Nikkhah, M., Ashrafiuon, H., and Fahimi, F., Robust control of underactuated bipeds using sliding modes, Robotica, 2007, vol. 25, no. 3, pp. 367–374.
Liu, L.M. and Liang, W., Adaptive asymptotic stable biped locomotion, 33rd Chinese IEEE Control Conference (CCC), 2014.
Hurmuzlu, Y., Génot, F., and Brogliato, B., Modeling, stability and control of biped robots—a general framework, Automatica, 2004, vol. 40, no. 10, pp. 1647–1664.
McGeer, T., Passive bipedal running, Proc. R. Soc. Lond. B: Biol. Sci., 1990, vol. 240, no. 1297, pp. 107–134.
Hu, Y., Yan, G., and Lin, Z., Stable running of a planar underactuated biped robot, Robotica, 2011, vol. 29, no. 5, pp. 657–665.
Dadashzadeh, B., et al., Stable active running of a planar biped robot using Poincare map control, Adv. Rob., 2014, vol. 28, no. 4, pp. 231–244.
Hamed, K.A., Buss, B.G., and Grizzle, J.W., Exponentially stabilizing continuous-time controllers for periodic orbits of hybrid systems: Application to bipedal locomotion with ground height variations, Int. J. Rob. Res., 2015.
Bartoszewicz, A., Discrete-time quasi-sliding-mode control strategies, IEEE Transactions on Industrial Electronics, 1998, vol. 45, no. 4, pp. 633–637.
Hu, J., et al., Robust sliding mode control for discrete stochastic systems with mixed time delays, randomly occurring uncertainties, and randomly occurring nonlinearities, IEEE Trans. Ind. Electron., 2012, vol. 59, no. 7, pp. 3008–3015.
Khandekar, A., Malwatkar, G., and Patre, B., Discrete sliding mode control for robust tracking of higher order delay time systems with experimental application, ISA Trans., 2013, vol. 52, no. 1, pp. 36–44.
Sarpturk, S.Z., Istefanopulos, Y., and Kaynak, O., On the stability of discrete-time sliding mode control systems, IEEE Trans. Autom. Control, 1987, vol. 32, no. 10, pp. 930–932.
Chang, J.L., Discrete sliding-mode control of mimo linear systems, Asian J. Control, 2002, vol. 4, no. 2, pp. 217–222.
Yu, X., et al., An invariant-manifold-based method for chaos control, IEEE Trans. Circuits Syst. I: Fundam. Theory Appl., 2001, vol. 48, no. 8, pp. 930–937.
Spurgeon, S., Hyperplane design techniques for discrete-time variable structure control systems, Int. J. Control, 1992, vol. 55, no. 2, pp. 445–456.
Chen, Y.-P. and Chang, J.-L., A new method for constructing sliding surfaces of linear time-invariant systems, Int. J. Syst. Sci., 2000, vol. 31, no. 4, pp. 417–420.
Author information
Authors and Affiliations
Corresponding author
Additional information
The article is published in the original.
About this article
Cite this article
Heydarnia, O., Dadashzadeh, B., Allahverdizadeh, A. et al. Discrete sliding mode control to stabilize running of a biped robot with compliant kneed legs. Aut. Control Comp. Sci. 51, 347–356 (2017). https://doi.org/10.3103/S0146411617050042
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.3103/S0146411617050042