Abstract
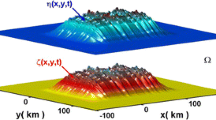
This paper describes a model for the generation of waves in the ocean by seismic bottom movements. A specific feature of this model is the use of curvilinear non-orthogonal sigma-coordinates. The results of numerical experiments aimed at studying the mechanisms of the generation of gravity waves by surface seismic waves propagating over the bottom are presented.




Similar content being viewed by others
REFERENCES
V. V. Titov, F. I. Gonzalez, H. O. Mofjeld, and A. J. Venturato, NOAA, NOAA Technical Memorandum OAR PMEL-124 (2003).
F. Imamura, A. C. Yalciner, and G. Ozyurt, Tsunami Modelling Manual (TUNAMI Model) (2006).
A. I. Zaytsev, A. G. Chernov, A. C. Yalciner, et al., MANUAL Tsunami Simulation/Visualization Code NAMI DANCE, Vers. 4.9 (2010).
O. V. Bulatov and T. G. Elizarova, Comput. Math. Math. Phys. 56, 661 (2016).
M. A. Nosov, Izv.—Atmos. Ocean. Phys. 50, 474 (2014).
P. A. Madsen, R. Murray, and O. R. Sørensen, Coast. Eng. 15, 371 (1991).
F. Løvholt, G. Pedersen, and S. Glimsdal, Open Oceanogr. J. 4, 71 (2010).
F. Shi, J. T. Kirby, J. C. Harris, et al., Ocean Model. 43–44, 36 (2012).
J. Kim, G. K. Pedersen, F. Løvholt, and R. J. LeVeque, Coast. Eng. 122, 75 (2017).
B. W. Levin and M. A. Nosov, Physics of Tsunamis, 2nd ed. (Springer, Netherlands, 2016).
K. Kajiura, Bull. Earthquake Res. Inst. 41, 535 (1963).
M. A. Nosov and S. V. Kolesov, Pure Appl. Geophys. 168, 1223 (2011).
I. V. Fain and E. A. Kulikov, Vychisl. Tekhnol. 16, 111 (2011).
M. A. Nosov and K. A. Sementsov, Izv.—Atmos. Ocean. Phys. 50, 539 (2014). https://doi.org/10.1134/S0001433814050089
T. Ohmachi, H. Tsukiyama, and H. Matsumoto, Bull. Seismol. Soc. Am. 91, 1898 (2001).
B. H. Choi, E. Pelinovsky, D. C. Kim, et al., Nonlin. Processes Geophys. 15, 489 (2008).
T. Maeda and T. Furumura, Pure Appl. Geophys. 170, 109 (2013).
A. Kozelkov, A. Kurkin, E. Pelinovskii, and V. Kurulin, Fluid Dyn. 50, 306 (2015).
M. A. Nosov and S. V. Kolesov, Nat. Hazards Earth Syst. Sci. 7, 243 (2007).
A. Bolshakova, S. Inoue, S. Kolesov, et al., Russ. J. Earth. Sci. 12, ES2005 (2011). https://doi.org/10.2205/2011ES000509
S. V. Kolesov and M. A. Nosov, Uch. Zap. Fiz. F-ta Mosk. Univ., №3, 163904 (2016). http://uzmu.phys.msu.ru/abstract/2016/3/163904
M. A. Nosov and S. V. Kolesov, Math. Models Comput. Simul. 11, 679 (2019). https://doi.org/10.1134/S2070048219050156
N. A. Phillips, J. Meteorol. 14, 184 (1957).
A. F. Blumberg and G. L. Mellor, Coast. Estuarine Ser. 4, 1 (1987).
Y. Song and D. Haidvogel, J. Comput. Phys. 115, 228 (1994).
M. Kocyigit, R. Falconer, and B. Lin, Int. J. Numer. Methods Fluids 40, 1145 (2002).
A. F. Shchepetkin and J. C. McWilliams, Ocean Model. 9, 347 (2005).
A. Decoene and J.-F. Gerbeau, 2008. \(<\)hal-00275463\(>\).
A. V. Gusev, ‘‘A numerical model of the hydrodynamics of the ocean in curved coordinates to reproduce the circulation of the world ocean and its individual water areas,’’ Dissertation (Moscow, 2009).
N. A. Dianskii, Modeling of Ocean Circulation and Study of its Response to Short-Period and Long-Period Atmospheric Effects (Fizmatlit, Moscow, 2012) [in Russian].
R. Nagao, S. Inoue, and T. Ohmachi, J. Jpn. Soc. Civil Eng., Ser. B2 66, 301 (2010).
S. Murotani, M. Iwai, K. Satake, G. Shevchenko, and A. Loskutov, Pure Appl. Geophys. 172, 683 (2015).
M. A. Nosov, K. A. Sementsov, S. V. Kolesov, H. Matsumoto, and B. W. Levin, Dokl. Earth Sci. 461, 408 (2015). https://doi.org/10.1134/S1028334X15040121
K. A. Sementsov, M. A. Nosov, S. V. Kolesov, and Y. Wu, Mosc. Univ. Phys. Bull. 72, 614 (2017). https://doi.org/10.3103/S0027134917060145
K. A. Sementsov, S. V. Kolesov, M. A. Nosov, et al., Uch. Zap. Fiz. F-ta Mosk. Univ., №4, 1740504 (2017). http://uzmu.phys.msu.ru/abstract/2017/4/1740504
K. A. Sementsov, M. A. Nosov, S. V. Kolesov, and A. V. Bol’shakova, Uch. Zap. Fiz. F-ta Mosk. Univ., №5, 1850301 (2018). http://uzmu.phys.msu.ru/abstract/2018/5/1850301
L. D. Landau and E. M. Livshitz, Course of Theoretical Physics, Vol. 6: Fluid Mechanics (Nauka, Moscow, 1986; Pergamon, New York, 1987).
V. F. Butuzov, N. Ch. Krutitskaya, G. N. Medvedev, and A. A. Shishkin, Mathematical Analysis in Questions and Tasks, 5th ed. (Fizmatlit, Moscow, 2002) [in Russian].
Y.-Y. Li, B. Wang, and D.-H. Wang, Atmos. Ocean. Sci. Lett. 4, 157 (2011).
M. A. Nosov, A. V. Moshenceva, and S. V. Kolesov, Pure Appl. Geophys. 170, 1647 (2013).
M. A. Nosov, A. V. Bolshakova, and S. V. Kolesov, Pure Appl. Geophys. 171, 3515 (2014).
K. Aki and P. Richards, Quantitative Seismology (University Science Books, 2009), Vol. 1.
Y. Tanioka and K. Satake, Geophys. Res. Lett. 23, 861 (1996).
M. A. Nosov, Mosc. Univ. Phys. Bull. 47 (1), 110 (1992).
H. Matsumoto and Y. Kaneda, in Proceedings of the 11th SEGJ International Symposium, Yokohama, Japan, November 18–21, 2013 (2013), p. 493.
Funding
This work was financially supported by the Russian Foundation for Basic Research (grant no. 19-05-00351).
Author information
Authors and Affiliations
Corresponding authors
Additional information
Translated by E. Glushachenkova
About this article
Cite this article
Sementsov, K.A., Bolshakova, A.V. A Model for the Generation of Waves in the Ocean by Seismic Bottom Movements in Sigma-Coordinates. Moscow Univ. Phys. 75, 87–94 (2020). https://doi.org/10.3103/S0027134920010129
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.3103/S0027134920010129