Skip to main content
SpringerLink
Log in

Dynamics and control of humanoid robots: A geometrical approach

  • Research Article
  • Published:
Paladyn

Abstract

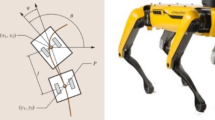
This paper reviews modern geometrical dynamics and control of humanoid robots. This general Lagrangian and Hamiltonian formalism starts with a proper definition of humanoid’s configuration manifold, which is a set of all robot’s active joint angles. Based on the ‘covariant force law’, the general humanoid’s dynamics and control are developed. Autonomous Lagrangian dynamics is formulated on the associated ‘humanoid velocity phase space’, while autonomous Hamiltonian dynamics is formulated on the associated ‘humanoid momentum phase space’. Neural-like hierarchical humanoid control naturally follows this geometrical prescription. This purely rotational and autonomous dynamics and control is then generalized into the framework of modern non-autonomous biomechanics, defining the Hamiltonian fitness function. The paper concludes with several simulation examples.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Ivancevic, V. Symplectic Rotational Geometry in Human Biomechanics. SIAM Rev. 46(3), 455–474 (2004).

    Article  MathSciNet  MATH  Google Scholar 

  2. Ivancevic, V., Ivancevic, T., Human-Like Biomechanics: A Unified Mathematical Approach to Human Biomechanics and Humanoid Robotics. Springer, Berlin, (2005).

    Google Scholar 

  3. Ivancevic, V., Sharma, S., Complexity in Human Bio-Mechanics. IJHR, 5(4), 679–698 (2008).

    Google Scholar 

  4. V. Ivancevic and T. Ivancevic, Human versus Humanoid Biodynamics, IJHR, 5(4), 699–713, (2008).

    MathSciNet  Google Scholar 

  5. Arnold, V.I., Mathematical Methods of Classical Mechanics. Springer, New York, (1978).

    MATH  Google Scholar 

  6. Abraham, R., Marsden, J., Foundations of Mechanics. Benjamin, Reading, MA, (1978).

    MATH  Google Scholar 

  7. Marsden, J.E., Ratiu, T.S., Introduction to Mechanics and Symmetry: A Basic Exposition of Classical Mechanical Systems. (2nd ed), Springer, New York, (1999).

    MATH  Google Scholar 

  8. Ivancevic, V., LieLagrangian model for realistic human biodynamics. IJHR, 3(2), 205–218 (2006).

    Google Scholar 

  9. Ivancevic, V., Ivancevic, T., Applied Differential Geometry: A Modern Introduction. World Scientific, Singapore, (2007).

    Book  MATH  Google Scholar 

  10. Ivancevic, V., Generalized Hamiltonian Biodynamics and Topology Invariants of Humanoid Robots, IJMMS, 31(9), 555–565 (2002).

    MathSciNet  MATH  Google Scholar 

  11. Ivancevic, V. & Beagley, N. Brain-like functor control machine for general humanoid biodynamics, IJMMS, 11, 1759–1779 (2005).

    MathSciNet  Google Scholar 

  12. Park, J., Chung, W.-K. Geometric Integration on Euclidean Group With Application to Articulated Multibody Systems. IEEE Trans. Rob. 21(5), 850–863 (2005).

    Article  Google Scholar 

  13. Ivancevic, T., Jet Methods in Time—Dependent Lagrangian Biomechanics, Cent. Eur. J. Phys. 8(5), (2010).

  14. Ivancevic, T. et al, Jet spaces in modern Hamiltonian biomechanics, Cent. Eur. J. Phys. 8(6), (2010).

  15. Ivancevic, T., Jet-Ricci Geometry of Time-Dependent Human Biomechanics, Int. J. Biomath. 3(1), 1–13, (2010).

    Article  MathSciNet  Google Scholar 

  16. Giachetta, G., Mangiarotti, L., Sardanashvily, G., New Lagrangian and Hamiltonian Methods in Field Theory, World Scientific, Singapore, (1997).

    MATH  Google Scholar 

  17. Wilkie, D.R., The mechanical properties of muscle. Brit. Med. Bull. 12, 177–182, (1956).

    Google Scholar 

  18. Hill, A.V.,The heat of shortening and the dynamic constants of muscle. Proc. Roy. Soc. B76, 136–195, (1938).

  19. Kosko, B., Neural Networks and Fuzzy Systems, A Dynamical Systems Approach to Machine Intelligence. Prentice-Hall, New York, (1992).

    MATH  Google Scholar 

  20. Houk, J.C., Regulation of stiffness by skeletomotor reflexes. Ann. Rev. Physiol. 41, 99–123, (1979).

    Article  Google Scholar 

  21. Houk, J.C., Buckingham, J.T., Barto, A.G., Models of the cerebellum and motor learning. Beh. Brain Sci. 19(3), 368–383, (1996).

    Google Scholar 

  22. Isidori, A., Nonlinear Control Systems, An Introduction (2nd ed.) Springer, Berlin, (1989).

    Google Scholar 

  23. Sastri, S.S., Isidori, A., Adaptive control of linearizable systems, IEEE Trans. Aut. Con. 34(11), 1123–1131, (1989).

    Article  Google Scholar 

  24. Ivancevic, V., Ivancevic, T., Neuro-Fuzzy Associative Machinery for Comprehensive Brain and Cognition Modelling. Springer, Berlin, (2007).

    Book  MATH  Google Scholar 

  25. Robertson, D.G.E., Caldwell, G.H., Hamill, J., Kamen, G., Whittlesey S.N., Research Methods in Biomechanics. Human Kinetics, Champaign, IL, (2004).

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Land Operation Division, Defence Science & Technology Organisation, Edinburgh, SA, 1500, Australia

    Vladimir G. Ivancevic & Tijana T. Ivancevic

  2. QLIWW IP Pty Ltd. & Tesla Science, Evolution Institute, Adelaide, Australia

    Vladimir G. Ivancevic & Tijana T. Ivancevic

Authors
  1. Vladimir G. Ivancevic
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Tijana T. Ivancevic
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Vladimir G. Ivancevic.

About this article

Cite this article

Ivancevic, V.G., Ivancevic, T.T. Dynamics and control of humanoid robots: A geometrical approach. Paladyn 1, 204–218 (2010). https://doi.org/10.2478/s13230-011-0007-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.2478/s13230-011-0007-7

Keywords

Search

Navigation