Skip to main content
SpringerLink
Log in

Empirical Regression Quantile Processes

  • Published:
Applications of Mathematics Aims and scope Submit manuscript

Abstract

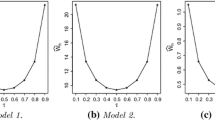
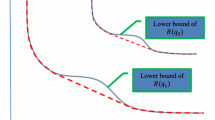
We address the problem of estimating quantile-based statistical functionals, when the measured or controlled entities depend on exogenous variables which are not under our control. As a suitable tool we propose the empirical process of the average regression quantiles. It partially masks the effect of covariates and has other properties convenient for applications, e.g. for coherent risk measures of various types in the situations with covariates.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. G. W. Bassett, Jr.: A property of the observations fit by the extreme regression quantiles. Comput. Stat. Data Anal. 6 (1988), 353–359.

    Article  MathSciNet  Google Scholar 

  2. G. W. Bassett, Jr., R. Koenker: An empirical quantile function for linear models with iid errors. J. Am. Stat. Assoc. 77 (1982), 405–415.

    MathSciNet  MATH  Google Scholar 

  3. C. Gutenbrunner, J. Jurečková: Regression rank scores and regression quantiles. Ann. Stat. 20 (1992), 305–330.

    Article  MathSciNet  Google Scholar 

  4. J. Hájek: Extension of the Kolmogorov-Smirnov test to regression alternatives. Proceedings of the International Research Seminar (L. LeCam, ed.). University of California Press, Berkeley, 1965, pp. 45–60.

    Google Scholar 

  5. L. A. Jaeckel: Estimating regression coefficients by minimizing the dispersion of the residuals. Ann. Math. Stat. 43 (1972), 1449–1458.

    Article  MathSciNet  Google Scholar 

  6. J. Jurečková: Averaged extreme regression quantile. Extremes 19 (2016), 41–49.

    Article  MathSciNet  Google Scholar 

  7. J. Jurečková, J. Picek: Two-step regression quantiles. Sankhyā 67 (2005), 227–252.

    MathSciNet  MATH  Google Scholar 

  8. J. Jurečková, J. Picek: Averaged regression quantiles. Contemporary Developments in Statistical Theory (S. Lahiri et al., eds.). Springer Proceedings in Mathematics and Statistics 68, Springer, Cham, 2014, pp. 203–216.

    Chapter  Google Scholar 

  9. J. Jurečková, J. Picek, M. Schindler: Robust Statistical Methods With R. CRC Press, Boca Raton, 2019.

    Book  Google Scholar 

  10. J. Jurečková, P. K. Sen, J. Picek: Methodology in Robust and Nonparametric Statistics. CRC Press, Boca Raton, 2013.

    MATH  Google Scholar 

  11. J. D. Kloke, J. W. McKean: Rfit: Rank-based estimation for linear models. The R Journal 4 (2012), 57–64.

    Article  Google Scholar 

  12. R. Koenker: Quantile Regression. Econometric Society Monographs 38, Cambridge University Press, Cambridge, 2005.

    Book  Google Scholar 

  13. R. Koenker: quantreg: Quantile Regression. R package version 5.51. Available at https://CRAN.R-project.org/package=quantreg.

  14. R. Koenker, G. Bassett, Jr.: Regression quantiles. Econometrica 46 (1978), 33–50.

    Article  MathSciNet  Google Scholar 

  15. S. Portnoy: Tightness of the sequence of empiric c.d.f. processes defined from regression fractiles. Robust and Nonlinear Time Series Analysis (J. Franke et al., eds.). Lecture Notes in Statistics 26, Springer, New York, 1984, pp. 231–245.

    Chapter  Google Scholar 

  16. S. Portnoy: Asymptotic behavior of the number of regression quantile breakpoints. SIAM J. Sci. Stat. Comput. 12 (1991), 867–883.

    Article  MathSciNet  Google Scholar 

  17. D. Ruppert, R. J. Carroll: Trimmed least squares estimation in the linear model. J. Am. Stat. Assoc. 75 (1980), 828–838.

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgement

We thank the reviewer for careful reading of our manuscript and for valuable comments.

Author information

Authors and Affiliations

  1. Department of Probability and Statistics, Faculty of Mathematics and Physics, Charles University, Sokolovská 83, 186 75, Praha 8, Czech Republic

    Jana Jurečková

  2. Institute of Information Theory and Automation, The Czech Academy of Sciences, Pod Vodárenskou věží 4, 182 00, Praha 8, Czech Republic

    Jana Jurečková

  3. Department of Applied Mathematics, Technical University, Studentská 2, 461 17, Liberec, Czech Republic

    Jan Picek & Martin Schindler

Authors
  1. Jana Jurečková
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jan Picek
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Martin Schindler
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Martin Schindler.

Additional information

The authors gratefully acknowledge the support of the Grant GACR 18-01137S.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Jurečková, J., Picek, J. & Schindler, M. Empirical Regression Quantile Processes. Appl Math 65, 257–269 (2020). https://doi.org/10.21136/AM.2020.0295-19

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.21136/AM.2020.0295-19

Keywords

MSC 2020

Search

Navigation