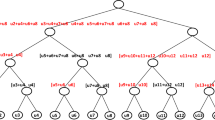
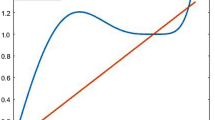
Abstract
The 3780-point FFT is a main component of the time domain synchronous OFDM (TDS-OFDM) system and the key technology in the Chinese Digital Multimedia/TV Broadcasting-Terrestrial (DMB-T) national standard. Since 3780 is not a power of 2, the classical radix-2 or radix-4 FFT algorithm cannot be applied directly. Hence, the Winograd Fourier transform algorithm (WFTA) and the Good-Thomas prime factor algorithm (PFA) are used to implement the 3780-point FFT processor. However, the structure based on WFTA and PFA has a large computational complexity and requires many DSPs in hardware implementation. In this paper, a novel 3780-point FFT processor scheme is proposed, in which a 60×63 iterative WFTA architecture with different mapping methods is imported to replace the PFA architecture, and an optimized CoOrdinate Rotation DIgital Computer (CORDIC) module is used for the twiddle factor multiplications. Compared to the traditional scheme, our proposed 3780-point FFT processor scheme reduces the number of multiplications by 45% at the cost of 1% increase in the number of additions. All DSPs are replaced by the optimized CORDIC module and ROM. Simulation results show that the proposed 3780-point FFT processing scheme satisfies the requirement of the DMB-T standard, and is an efficient architecture for the TDS-OFDM system.
Similar content being viewed by others
References
Abdullah, S., Haewoon, N., McDermot, M., Abraham, J., 2009. A High Throughput FFT Processor with No Multipliers. IEEE Int. Conf. on Computer Design, p.485–490. [doi:10.1109/ICCD.2009.5413113]
Adiono, T., Purba, R.S., 2009. Scalable Pipelined CORDIC Architecture Design and Implementation in FPGA. Int. Conf. on Electrical Engineering and Informatics, p.646–649. [doi:10.1109/ICEEI.2009.5254736]
Camarda, F., Prevotet, J.C., Nouvel, F., 2009. Implementation of a Reconfigurable Fast Fourier Transform Application to Digital Terrestrial Television Broadcasting. 19th Int. Conf. on Field Programmable Logic and Applications, p.353–358. [doi:10.1109/FPL.2009.5272266]
Cheng, C., Parhi, K.K., 2007. Low-cost fast VLSI algorithm for discrete Fourier transform. IEEE Trans. Circ. Syst. I, 54(4):791–806. [doi:10.1109/TCSI.2006.888772]
Cheng, G., Su, K., 2010. A 3780-point FFT Algorithm and Its FPGA Implementation. Int. Symp. on Next Generation Electronics, p.231–233. [doi:10.1109/ISNE.2010.5669154]
Cooley, J.W., Tukey, J.W., 1965. An algorithm for the machine calculation of complex Fourier series. Math. Comput., 19(90):297–301. [doi:10.1090/S0025-5718-1965-0178586-1]
Good, I.J., 1958. The interaction algorithm and practical Fourier series. J. R. Stat. Soc., 20(2):361–372.
Lakshmi, B., Dhar, A.S., 2008. Low Latency VLSI Architecture for the Radix-4 CORDIC Algorithm. IEEE Region 10 and 3rd Int. Conf. on Industrial and Information Systems, p.1–5. [doi:10.1109/ICIINFS.2008.4798377]
Liu, M., Crussiere, M., Helard, J.F., Pasquero, O.P., 2008. Analysis and Performance Comparison of DVB-T and DTMB Systems for Terrestrial Digital TV. 11th IEEE Int. Conf. on Communication Systems, p.1399–1404. [doi:10.1109/ICCS.2008.4737413]
Patterson, R.W., Mcclellan, J.H., 1978. Fixed-point error analysis of Winograd Fourier transform algorithms. IEEE Trans. Acoust. Speech Signal Process., 26(5):447–455. [doi:10.1109/TASSP.1978.1163134]
SAC (Standardization Administration of the People’s Republic of China), 2006. Framing Structure, Channel Coding and Modulation for Digital Television Terrestrial Broadcasting System. Standards Press of China, Beijing, China (in Chinese).
Silverman, H., 1977. An introduction to programming the Winograd Fourier transform algorithm (WFTA). IEEE Trans. Acoust. Speech Signal Process., 25(2):152–165. [doi:10.1109/TASSP.1977.1162924]
Song, J., Yang, Z., Yang, L., Gong, K., Pan, C., Wang, J., Wu, Y., 2007. Technical review on Chinese Digital Terrestrial Television Broadcasting Standard and measurements on some working modes. IEEE Trans. Broadcast., 53(1):1–7. [doi:10.1109/TBC.2007.891835]
Volder, J.E., 1959. The CORDIC trigonometric computing technique. IEEE Trans. Electron. Comput., 8(3):330–334. [doi:10.1109/TEC.1959.5222693]
Winograd, S., 1976. On computing the discrete Fourier transform. PNAS, 73(4):1005–1006. [doi:10.1073/pnas.73.4.1005]
Wu, C., Wang, R., Yen, C., 1994. Adder-based SIMD-systolic architectures and VLSI chip for computing the Winograd small FFT algorithms. Int. J. Electron., 76(6):1135–1149. [doi:10.1080/00207219408926023]
Xing, Q., Zhu, Q., Sun, S., 1996. Iterative Structure of Winograd FFT Algorithm. Conf. on Precision Electromagnetic Measurements, p.57–58. [doi:10.1109/CPEM.1996.546557]
Yang, J., Wang, K., Zou, Z., 2007. DVB-S2 inner receiver design for broadcasting mode. J. Zhejiang Univ.-Sci. A, 8(1):28–35. [doi:10.1631/jzus.2007.A0028]
Yang, X., Du, W., Yang, Z., Lv, R., Wang, X., 2010. Hardware Design and Implementation of 3780 Points FFT Based on FPGA in DTTB. 4th Int. Conf. on Application of Information and Communication Technologies, p.1–4. [doi:10.1109/ICAICT.2010.5611806]
Yang, Z., Hu, Y., Pan, C., Yang, L., 2002. Design of a 3780-point IFFT processor for TDS-OFDM. IEEE Trans. Broadcast., 48(1):57–61. [doi:10.1109/11.992857]
Author information
Authors and Affiliations
Corresponding author
Additional information
Project supported by the National Natural Science Foundation of China (No. 61071129) and the Science and Technology Department of Zhejiang Province, China (Nos. 2008C21088, 2011R10035, and 2011R09003-06)
Rights and permissions
About this article
Cite this article
Leng, Jn., Xie, L., Chen, Hf. et al. A novel 3780-point FFT processor scheme for the time domain synchronous OFDM system. J. Zhejiang Univ. - Sci. C 12, 1021–1030 (2011). https://doi.org/10.1631/jzus.C1100071
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1631/jzus.C1100071
Key words
- 3780
- CoOrdinate Rotation DIgital Computer (CORDIC)
- Digital Multimedia/TV Broadcasting-Terrestrial (DMB-T)
- FFT
- Time domain synchronous OFDM (TDS-OFDM)
- Winograd Fourier transform algorithm (WFTA)