Skip to main content
SpringerLink
Log in

Curve smoothing using a continuous function

连续函数式曲线光滑法

  • Published:
Journal of Zhejiang University-SCIENCE A Aims and scope Submit manuscript

Abstract

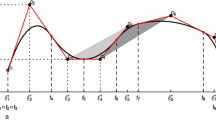
Current curve smoothing technologies provide a smoothed curve by joining together separate curves that have certain degrees of continuity at junctions. These technologies have found many applications in science and engineering. However, none of them can provide a smoothed curve using a single continuous function for arbitrary segmental curves. This paper reports a new approach that can be used to construct a single continuous function that joins an arbitrary number of different segmental curves, with the required degree of continuity at all junctions. The smoothness of transition at different junctions can be controlled by separate parameters to suit different needs. The combined continuous function can approach the original segmental functions asymptotically or match the original segmental functions “exactly” inside each segment by adjusting the smoothness parameter. This new approach may also find application outside the scope of curve smoothing/curving fitting in the future.

概要

目的

用连续函数实现无限接近原始非连续曲线的光滑。

创新点

首次提出用一个连续函数替代原来由任意多非连 续区域函数构成的函数。该方法可视为一种新的 函数光滑算法。

方法

1. 通过引入特殊的区域变量,并用该区域变量替 代原函数自变量的方法,将区域函数改造成在该 区域无限接近原函数而在区域外取值常数的函 数。2. 把所有的区域函数相乘得到一个连续函数 的方程。

结论

1. 由任意多非连续区域函数构成的函数可以改造 成一个连续函数。2. 该连续函数在原非连续边界 的光滑程度可以由各个边界上独立的参数按需 调整。3. 该方法产生的连续函数没有摆动现象, 其形状与原始区域函数无限接近。该方程在数学 上是连续的,同时无限接近原始非连续函数,包 括原来在边界上函数值的非连续。

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  • Cai HH, Wang GJ, 2009. A new method in highway route design: joining circular arcs by a single C-Bézier curve with shape parameter. Journal of Zhejiang University-SCIENCE A, 10(4):562–569. https://doi.org/10.1631/jzus.A0820267

    Article  MATH  Google Scholar 

  • CEB (Comite Euro-International du Beton), 1993. CEB-FIP Model Code 1990: Design Code FIB-Fédération Internationale du Beton.

    Book  Google Scholar 

  • Emami MM, Arezoo B, 2010. A look-ahead command generator with control over trajectory and chord error for NURBS curve with unknown arc length. Computer-Aided Design, 42(7):625–632. https://doi.org/10.1016/j.cad.2010.04.001

    Article  Google Scholar 

  • Erkorkmaz K, Altintas Y, 2001. High speed CNC system design. Part I: jerk limited trajectory generation and quintic spline interpolation. International Journal of Machine Tools and Manufacture, 41(9):1323–1345. https://doi.org/10.1016/S0890-6955(01)00002-5

    Google Scholar 

  • Feng J, Li Y, Wang Y, et al., 2010. Design of a real-time adaptive NURBS interpolator with axis acceleration limit. The International Journal of Advanced Manufacturing Technology, 48(1–4): 227–241. https://doi.org/10.1007/s00170-009-2261-y

    Article  Google Scholar 

  • Fraichard T, Scheuer A, 2004. From Reeds and Shepp’s to continuous-curvature paths. IEEE Transactions on Robotics, 20(6):1025–1035. https://doi.org/10.1109/TRO.2004.833789

    Article  Google Scholar 

  • Giuffre A, Pinto PE, 1970. Il comportamento del cemento armato per sollecitazioni cicliche di forte intensita. Giornale del Genio Civile, 5:391–408 (in Italian).

    Google Scholar 

  • Hognestad E, 1951. A Study of Combined Bending and Axial Load in Reinforced Concrete Members. Bulletin Series No. 399, Engineering Experiment Station, University of Illinois, Urbana, USA.

    Google Scholar 

  • Huh UY, Chang SR, 2014. A G² continuous path-smoothing algorithm using modified quadratic polynomial interpolation. International Journal of Advanced Robotic Systems, 11(2):1–11. https://doi.org/10.5772/57340

    Article  Google Scholar 

  • Lin MT, Tsai MS, Yau HT, 2007. Development of a dynamicsbased NURBS interpolator with real-time look-ahead algorithm. International Journal of Machine Tools and Manufacture, 47(15):2246–2262. https://doi.org/10.1016/j.ijmachtools.2007.06.005

    Article  Google Scholar 

  • Liu X, Ahmad F, Yamazaki K, et al., 2005. Adaptive interpolation scheme for NURBS curves with the integration of machining dynamics. International Journal of Machine Tools and Manufacture, 45(4–5): 433–444. https://doi.org/10.1016/j.ijmachtools.2004.09.009

    Article  Google Scholar 

  • Magid E, Keren D, Rivlin E, et al., 2006. Spline-based robot navigation. Proceedings of the 2006 IEEE/RSJ International Conference on Intelligent Robots and Systems, p.2296-2301.

    Book  Google Scholar 

  • Nam SH, Yang MY, 2004. A study on a generalized parametric interpolator with real-time jerk-limited acceleration. Computer-Aided Design, 36(1):27–36. https://doi.org/10.1016/S0010-4485(03)00066-6

    Article  Google Scholar 

  • Pan J, Wu YF, 2014. Analytical modeling of bond behavior between FRP plate and concrete. Composites Part B: Engineering, 61:17–25. https://doi.org/10.1016/j.compositesb.2014.01.026

    Article  Google Scholar 

  • Park R, Paulay T, 1975. Reinforced Concrete Structures. John Wiley & Sons, New York.

    Book  Google Scholar 

  • Pateloup V, Duc E, Ray P, 2010. Bspline approximation of circle arc and straight line for pocket machining. Computer-Aided Design, 42(9):817–827. https://doi.org/10.1016/j.cad.2010.05.003

    Article  Google Scholar 

  • Richard RM, Abbott BJ, 1975. Versatile elastic-plastic stressstrain formula. Journal of the Engineering Mechanics Division, 101:511–515.

    Google Scholar 

  • Roy R, Bodduna K, Kumari N, et al., 2015. A fast and efficient mesh smoothing algorithm for 3D graphical models using cubic B-splines. In: Information Systems Design and Intelligent Applications. Springer, New Delhi, India, p.467-474. https://doi.org/10.1007/978-81-322-2247-7_48

    Book  Google Scholar 

  • Walton DJ, Meek DS, 2009. G2 blends of linear segments with cubics and pythagorean-hodograph quintics. International Journal of Computer Mathematics, 86(9):1498–1511. https://doi.org/10.1080/00207160701828157

    Article  MathSciNet  MATH  Google Scholar 

  • Walton DJ, Meek DS, 2010. Cubic Bézier spiral segments for planar G2 curve design. Proceedings of the 7th International Conference on Computer Graphics, Virtual Reality, Visualisation and Interaction in Africa, ACM, p.21-26.

    Google Scholar 

  • Wang JB, Yau HT, 2009. Real-time NURBS interpolator: application to short linear segments. International Journal of Advanced Manufacturing Technology, 41(11-12): 1169–1185. https://doi.org/10.1007/s00170-008-1564-8

    Article  Google Scholar 

  • Wu G, Sun ZY, Wu ZS, et al., 2012. Mechanical properties of steel-FRP composite bars (SFCBs) and performance of SFCB reinforced concrete structures. Advances in Structural Engineering, 15(4):625–636. https://doi.org/10.1260/1369-4332.15.4.625

    Article  Google Scholar 

  • Yang K, Sukkarieh S, 2010. An analytical continuouscurvature path-smoothing algorithm. IEEE Transactions on Robotics, 26(3):561–568. https://doi.org/10.1109/TRO.2010.2042990

    Article  Google Scholar 

  • Yang X, Chen ZC, 2006. A practicable approach to G1 biarc approximations for making accurate, smooth and nongouged profile features in CNC contouring. Computer-Aided Design, 38(11):1205–1213. https://doi.org/10.1016/j.cad.2006.07.006

    Article  Google Scholar 

  • Yau HT, Wang JB, 2007. Fast Bezier interpolator with realtime look ahead function for high-accuracy machining. International Journal of Machine Tools and Manufacture, 47(10):1518–1529. https://doi.org/10.1016/j.ijmachtools.2006.11.010

    Article  Google Scholar 

  • Yeh SS, Hsu PL, 2002. Adaptive-feedrate interpolation for parametric curves with a confined chord error. Computer-Aided Design, 34(3):229–237. https://doi.org/10.1016/S0010-4485(01)00082-3

    Article  Google Scholar 

  • Zhang LB, You YP, He J, et al., 2011. The transition algorithm based on parametric spline curve for high-speed machining of continuous short line segments. International Journal of Advanced Manufacturing Technology, 52(1–4): 245–254. https://doi.org/10.1007/s00170-010-2718-z

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Engineering, RMIT University, Carlton, Victoria, 3053, Australia

    Yu-fei Wu & Zhi-dong Li

  2. Guangzhou Metro Design and Research Institute Co. Ltd., Guangzhou, 510010, China

    Liang He

  3. Department of Architecture and Civil Engineering, City University of Hong Kong, Kowloon, Hong Kong, China

    Liang He

Authors
  1. Yu-fei Wu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Liang He
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Zhi-dong Li
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yu-fei Wu.

Additional information

Project supported by the National Natural Science Foundation of China (No. 51378449)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wu, Yf., He, L. & Li, Zd. Curve smoothing using a continuous function. J. Zhejiang Univ. Sci. A 19, 304–314 (2018). https://doi.org/10.1631/jzus.A1700502

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1631/jzus.A1700502

Keywords

关键词

CLC number

Search

Navigation