Skip to main content
SpringerLink
Log in

Eccentricity and thermoviscous effects on ultrasonic scattering from a liquid-coated fluid cylinder

  • Published:
Journal of Zhejiang University-SCIENCE A Aims and scope Submit manuscript

Abstract

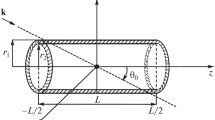
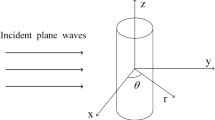
Calculation of the scattered field of the eccentric scatterers is an old problem with numerous applications. This study considers the interaction of a plane compressional sound wave with a liquid-encapsulated thermoviscous fluid cylinder submerged in an unbounded viscous thermally conducting medium. The translational addition theorem for cylindrical wave functions, the appropriate wave field expansions and the pertinent boundary conditions are employed to develop a closed-form solution in the form of infinite series. The analytical results are illustrated with a numerical example in which the compound cylinder is insonified by a plane sound wave at selected angles of incidence in a wide range of dimensionless frequencies. The backscattered far-field acoustic pressure amplitude and the spatial distribution of the total acoustic pressure in the vicinity of the cylinder are evaluated and discussed for representative values of the parameters characterizing the system. The effects of incident wave frequency, angle of incidence, fluid thermoviscosity, core eccentricity and size are thoroughly examined. Limiting case involving an ideal compressible liquid-coated cylinder is considered and fair agreement with a well-known solution is established.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  • Abramowitz, M., Stegun, I.A., 1965. Handbook of Mathematical Functions. National Bureau of Standards. Washington, DC.

    MATH  Google Scholar 

  • Alemar, J.D., Delsanto, P.P., Rosario, E., Nagel, A., Uberal, H., 1986a. Spectral analysis of the scattering of acoustic waves from a fluid cylinder, I: Denser fluid loading. Acustica, 61:1–6.

    MATH  Google Scholar 

  • Alemar, J.D., Delsanto, P.P., Rosario, E., Nagel, A., Uberal, H., 1986b. Spectral analysis of the scattering of acoustic waves from a fluid cylinder, II: Denser fluid inside. Acustica, 61:7–13.

    MATH  Google Scholar 

  • Babick, F., Hinze, F., Ripperger, S., 2000. Dependence of ultrasonic attenuation on the material properties. Colloids and Surfaces A: Physicochemical and Engineering Aspects, 172(1–3):33–46. [doi:10.1016/S0927-7757(00)00571-9]

    Article  Google Scholar 

  • Bailey, D.H., 1995. A FORTRAN-90 based multiprecision system. ACM Trans. Math. Soft., 21(4):379–387. [doi:10.1145/212066.212075]

    Article  MATH  Google Scholar 

  • Boag, A., Levitan, Y., Boag, A., 1988. Analysis of acoustic scattering from fluid cylinders using a multifilament source model. J. Acoust. Soc. Am., 83(1):1–8. [doi:10.1121/1.396422]

    Article  Google Scholar 

  • Cai, L.W., 2004. Multiple scattering in single scatterers. J. Acoust. Soc. Am., 115(3):986–995. [doi:10.1121/1.1643362]

    Article  Google Scholar 

  • Chandra, K., Thompson, C., 1992. Improved perturbation method for scattering from a fluid cylinder. J. Acoust. Soc. Am., 92(2):1047–1055. [doi:10.1121/1.404034]

    Article  Google Scholar 

  • Chung, S.K., Trinh, E.H., 1998. Containerless protein crystal growth in rotating levitated drops. J. Cryst. Growth, 194(3–4):384–397. [doi:10.1016/S0022-0248(98)00542-9]

    Article  Google Scholar 

  • Danila, E.B., Conoir, J.M., Izbicki, J.L., 1995. Generalized Debye series expansion: Treatment of the concentric and nonconcentric cylindrical fluid-fluid interfaces. J. Acoust. Soc. Am., 98(6):3326–3342. [doi:10.1121/1.413820]

    Article  Google Scholar 

  • Danila, E.B., Conoir, J.M., Izbicki, J.L., 1998. Generalized Debye series expansion. Part II, Treatment of eccentric fluid-solid cylindrical interfaces. Acta Acustica, 84:38–44.

    Google Scholar 

  • Doi, T., Koster, J.N., 1993. Thermocapillary convection in two immiscible liquid layers with free surface. Phys. Fluids A, 5(8):1914–1927.

    Article  MATH  Google Scholar 

  • Dongarra, J., Bunch, J., Moler, C., Stewart, G.W., 1979. LINPACK User’s Guide. SIAM.

  • Eyer, A., Leiste, H., 1985. Striation-free silicon crystal by float-zoning with surface coated melt. J. Cryst. Growth, 71(1):249–252. [doi:10.1016/0022-0248(85)90073-9]

    Article  Google Scholar 

  • Faran, J.J., 1951. Sound scattering by solid cylinders and spheres. J. Acoust. Soc. Am., 23(4):405–418. [doi:10.1121/1.1906780]

    Article  MathSciNet  Google Scholar 

  • Gao, J.R., Wei, B.B., 1999. Containerless solidification of undercooled NdFeZrB alloy droplets in a drop tube. J. Alloys Compd., 285(1–2):229–232. [doi:10.1016/S0925-8388(98)00870-6]

    Article  Google Scholar 

  • Hasegawa, T., Yasutaka, H., Akio, H.A., Hideki, N., Massahiko, K., 1993. Acoustic radiation pressure acting on spherical and cylindrical shells. J. Acoust. Soc. Am., 93(1):154–160. [doi:10.1121/1.405653]

    Article  Google Scholar 

  • Hasheminejad, M., Geers, T.L., 1993. Modal impedance for two spheres in a thermoviscous fluid. J. Acoust. Soc. Am., 94(4):2205–2214. [doi:10.1121/1.407491]

    Article  Google Scholar 

  • Hasheminejad, M., Azarpeyvand, M., 2003. Energy distribution and radiation loading of a cylindrical source suspended within a nonconcentric fluid cylinder. Acta Mechanica, 164(1–2):15–30. [doi:10.1007/s00707-003-0014-9]

    Article  MATH  Google Scholar 

  • Hasheminejad, M., Badsar, A., 2004. Acoustic scattering by a pair of poroelastic spheres. Quart. J. Mech. Appl. Math., 57(1):95–113. [doi:10.1093/qjmam/57.1.95]

    Article  MathSciNet  MATH  Google Scholar 

  • Janele, P.J., Mioduchowski, A., Haddow, J.B., 1991. A note on finite dynamic deformation of concentric cylinders. Int. J. Eng. Sci., 29(12):1585–1592. [doi:10.1016/0020-7225(91)90128-P]

    Article  Google Scholar 

  • Johnson, D.T., 2002. Viscous effects in liquid encapsulated liquid bridges. Int. J. Heat Fluid Flow, 23(6):844–854. [doi:10.1016/S0142-727X(02)00186-8]

    Article  Google Scholar 

  • Kanevskii, I.N., Surikov, B.S., 1976. Two-layer acoustic lenses. Acoustics, 22:292–294.

    Google Scholar 

  • Lamb, H., 1945. Hydrodynamics. Dover.

  • Lane, M., Forest, K.T., Lyons, E.A., Bavister, B.D., 1999. Live births following vitrification of hamster embryos using a novel containerless technique. Theriogenology, 51(1):167. [doi:10.1016/S0093-691X(99)91726-0]

    Article  Google Scholar 

  • Li, M.W., Zeng, D.L., Zhu, T.X., 2002. Instability of the Marangoni convection in a liquid bridge with liquid encapsulation under microgravity condition. Int. J. Heat Mass Transfer, 45(1):157–164. [doi:10.1016/S0017-9310(01)00125-9]

    Article  MATH  Google Scholar 

  • Li, Y.R., Liu, Y.J., Peng, L., Wang, Y., 2006. Three-dimensional oscillatory thermocapillary flow in encapsulated liquid bridge. Phys. Fluids, 18(7):074108-1–074108-6. [doi:10.1063/1.2227051]

    Google Scholar 

  • Lin, W.H., Raptis, A.C., 1983. Acoustic scattering by elastic solid cylinders and spheres in viscous fluids. J. Acoust. Soc. Am., 73(3):736–748. [doi:10.1121/1.389039]

    Article  MATH  Google Scholar 

  • Lorber, B., Giege, R., 1996. Containerless protein crystallization in floating drops—Application to crystal-growth monitoring under reduced nucleation conditions. J. Cryst. Growth, 168(1–4):204–215. [doi:10.1016/0022-0248(96)00356-9]

    Article  Google Scholar 

  • Mai, J., Yamane, R., Früh, W.G., Oshima, S., Ando, A., 2002. Unstable waves at the interface of a diamagnetic liquid column contained in a magnetic fluid. European Journal of Mechanics-B/Fluids, 21(2):237–246. [doi:10.1016/S0997-7546(01)01168-2]

    Article  MATH  Google Scholar 

  • Marr-Lyon, M.J., Thiessen, D.B., Marston, P.L., 1997. Stabilization of a cylindrical capillary bridge far beyond the Rayleigh-Plateau limit using acoustic radiation pressure and active feedback. J. Fluid Mech., 351:345–357. [doi:10.1017/S002211209700726X]

    Article  Google Scholar 

  • Marr-Lyon, M.J., Thiessen, D.B., Blonigen, F.J., Marston, P.L., 2000. Stabilization of electrically conducting capillary bridges using feedback control of radial electrostatic stresses and the shapes of extended bridges. Phys. Fluids, 12(5):986–995. [doi:10.1063/1.870354]

    Article  MATH  Google Scholar 

  • Marr-Lyon, M.J., Thiessen, D.B., Marston, P.L., 2001. Passive stabilization of capillary bridges in air with acoustic radiation pressure. Phys. Rev. Lett., 86(11):2293–2296. [doi:10.1103/PhysRevLett.86.2293]

    Article  Google Scholar 

  • Montanero, J.M., 2003. Theoretical analysis of the vibration of axisymmetric liquid bridges of arbitrary shape. Theoret. Comput. Fluid Dynamics, 16(3):171–186. [doi:10.1007/s00162-002-0077-6]

    Article  MathSciNet  MATH  Google Scholar 

  • Montanero, J.M., Cabezas, G., Acero, J., Perales, J.M., 2002. Theoretical and experimental analysis of the equilibrium contours of liquid bridges of arbitrary shape. Phys. Fluids, 14(2):682–693. [doi:10.1063/1.1427922]

    Article  MathSciNet  MATH  Google Scholar 

  • Morse, P., Ingard, K., 1968. Theoretical Acoustics. McGraw-Hill.

  • Morse, S.F., Feng, Z.W., Marston, P.L., 1995. High-frequency threshold processes for leaky waves on cylinders of variable thickness: Fluid shell case. J. Acoust. Soc. Am., 98(5):2928. [doi:10.1121/1.414135]

    Article  Google Scholar 

  • Moseler, M., Landman, U., 2000. Formation, stability, and breakup of nanojets. Science, 289(5482):1165–1169. [doi:10.1126/science.289.5482.1165]

    Article  Google Scholar 

  • Nagashio, K., Takamura, Y., Kuribayashi, K., Shiohara, Y., 1999. Microstructural control of NdBa3Cu3O7-delta superconducting oxide from highly undercooled melt by containerless processing. J. Cryst. Growth, 200(1–2):118–125. [doi:10.1016/S0022-0248(98)01258-5]

    Article  Google Scholar 

  • Perales, J.M., Meseguer, J., 1992. Theoretical and experimental study of the vibration of axisymmetric viscous liquid bridges. Phys. Fluids A, 4(6):1110–1130.

    Article  Google Scholar 

  • Rayleigh, L., 1945. Theory of Sound. Dover.

  • Reese, J.M., Thompson, W., 1986. Acoustic diffraction by a variable thickness fluid layer. J. Acoust. Soc. Am., 80(6):1810–1815. [doi:10.1121/1.394295]

    Article  Google Scholar 

  • Rhim, W.K., Ohsaka, K., Paradis, P.F., Spjut, R.E., 1999. Noncontact technique for measuring surface-tension and viscosity of molten materials using high-temperature electrostatic levitation. Rev. Sci. Instrum., 70(6):2796–2801. [doi:10.1063/1.1149797]

    Article  Google Scholar 

  • Roumeliotis, J.A., Kakogiannos, B., 1995. Acoustic scattering from an infinite cylinder of small radius coated by a penetrable one. J. Acoust. Soc. Am., 97(4):2074–2081. [doi:10.1121/1.412000]

    Article  Google Scholar 

  • Roumeliotis, J.A., Ziotopoulos, A.P., Kokkorakis, G.C., 2001. Acoustic scattering by a circular cylinder parallel with another of small radius. J. Acoust. Soc. Am., 109(3):870–877. [doi:10.1121/1.1348296]

    Article  Google Scholar 

  • Rousselot, J.L., 1994. Field diffracted by a fluid cylinder: Comparison between the geometrical theory of diffraction and a model solution. Acustica, 80:14–20.

    MATH  Google Scholar 

  • Sanz, A., 1985. The influence of the outer bath in the dynamics of axisymmetric liquid bridges. J. Fluid. Mech., 156:101–140. [doi:10.1017/S0022112085002014]

    Article  MATH  Google Scholar 

  • Schuster, G.T., 1990. A fast exact numerical solution for the acoustic response of concentric cylinders with penetrable interfaces. J. Acoust. Soc. Am., 87(2):495–502. [doi:10.1121/1.398919]

    Article  Google Scholar 

  • Scotti, T., Wirgin, A., 2004. Reconstruction of the three mechanical material constants of a lossy fluid-like cylinder from low-frequency scattered acoustic fields. Comptes Rendus Mécanique, 332(9):717–724. [doi:10.1016/j.crme.2004.03.018]

    Article  Google Scholar 

  • Shaw, R.P., Tai, G., 1974. Time harmonic acoustic radiation from nonconcentric circular cylinder. J. Acoust. Soc. Am., 56(5):1437–1443. [doi:10.1121/1.1903462]

    Article  MATH  Google Scholar 

  • Sinai, J., Waag, R.C., 1988. Ultrasonic scattering by two concentric cylinders. J. Acoust. Soc. Am., 83(5):1728–1735. [doi:10.1121/1.396505]

    Article  Google Scholar 

  • Stratton, J.A., 1941. Electromagnetic Theory. McGraw-Hill.

  • Temkin, S., 1981. Elements of Acoustics. Wiley, New York.

    Google Scholar 

  • Thiessen, D.B., Marr-Lyon, M.J., Marston, P.L., 2002. Active electrostatic stabilization of liquid bridges in low gravity. J. Fluid Mech., 457:285–294. [doi:10.1017/S0022112002007760]

    Article  MATH  Google Scholar 

  • Varadan, V.V., Ma, Y., Varadan, V.K., Lakhtakia, A., 1991. Scattering of Waves by Spheres and Cylinders. In: Varadan, V.V., Lakhtakia, A., Varadan, V.K. (Eds.), Field Representation and Introduction to Scattering. Elsevier, Amsterdam, p.211–324.

    Google Scholar 

  • Viviani, A., Golia, C., 2003. Thermocapillary flows in two-fluids liquid bridges. Acta Astronautica, 53(11):879–897. [doi:10.1016/S0094-5765(02)00240-0]

    Article  Google Scholar 

  • Walker, J.S., Henry, D., BenHadid, H., 2002. Magnetic stabilization of the buoyant convection in the liquid-encapsulated Czochralski process. J. Cryst. Growth, 243(1):108–116. [doi:10.1016/S0022-0248(02)01487-2]

    Article  Google Scholar 

  • Wei, W., Thiessen, D.B., Marston, P.L., 2004. Acoustic radiation force on a compressible cylinder in a standing wave. J. Acoust. Soc. Am., 116(1):201–208. [doi:10.1121/1.1753291]

    Article  Google Scholar 

  • Zayas, F., Alexander, J.I.D., Meseguer, J., Ramus, J.F., 2000. On the stability limits of long nonaxisymmetric cylindrical liquid bridges. Phys. Fluids, 12(5):979–985. [doi:10.1063/1.870353]

    Article  MathSciNet  MATH  Google Scholar 

  • Zhang, S., Jin, J., 1996. Computation of Special Functions. John Wiley & Sons.

Download references

Author information

Authors and Affiliations

  1. Acoustics Research Lab., Department of Mechanical Engineering, Iran University of Science and Technology, Narmak, Tehran, 16844, Iran

    Seyyed M. Hasheminejad & M. A. Alibakhshi

Authors
  1. Seyyed M. Hasheminejad
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. M. A. Alibakhshi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Seyyed M. Hasheminejad.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Hasheminejad, S.M., Alibakhshi, M.A. Eccentricity and thermoviscous effects on ultrasonic scattering from a liquid-coated fluid cylinder. J. Zhejiang Univ. Sci. A 9, 65–78 (2008). https://doi.org/10.1631/jzus.A072053

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1631/jzus.A072053

Key words

CLC number

Search

Navigation