Abstract
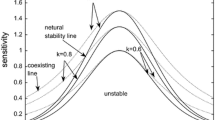
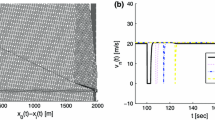
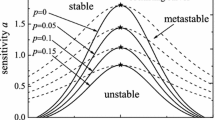
Effects of the speed relaxation time on the optimal velocity car-following model (OVM) with delay time due to driver reaction time proposed by Bando et al. (1995) were studied by numerical methods. Results showed that the OVM including the delay is not physically sensitive to the speed relaxation times. A modified car-following model is proposed to overcome the deficiency. Analyses of the linear stability of the modified model were conducted. It is shown that coexisting flows appear if the initial homogeneous headway of the traffic flow is between critical values. In addition, phase transitions occur on varying the initially homogeneous headway.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Bando, M., Hasebe, K., Nakayama, A., Shibata, A., Sugiyama, Y., 1995. Dynamic model of traffic congestion and numerical simulation. Physical Reviews E, 51(2):1035–1042. [doi:10.1103/PhysRevE.51.1035]
Bando, M., Hasebe, K., Nakanishi, K., Nakayama, A., 1998. Analysis of optimal velocity model with explicit delay. Physical Reviews E, 58(5):5429–5435. [doi:10.1103/PhysRevE.58.5429]
Davis, L.C., 2003. Modifications of the optimal velocity traffic model to include delay due to driver reaction time. Physica A, 319:557–567. [doi:10.1016/S0378-4371(02) 01457-7]
Helbing, D., Tilch, B., 1998. Generalized force model of traffic dynamics. Physical Review E, 58(1):133–138. [doi:10.1103/PhysRevE.58.133]
Jiang, R., Wu, Q.S., 2003. First-and second-phase transitions from free flow to synchronized flow. Physica A, 322:676–684. [doi:10.1016/S0378-4371(02)01802-2]
Kerner, B.S., Rehborn, H., 1997. Experimental properties of phase transitions in traffic flow. Physical Review E, 79(20):4030–4033.
Nagatani, T., 1998. Thermodynamic theory for the jamming transition in traffic flow. Physical Review E, 58(4):4271–4276. [doi:10.1103/PhysRevE.58.4271]
Treiber, M., Henneche, A., Helbing, D., 2000. Congested traffic states in empirical observations and microscopic simulations. Physical Review E, 62(2):1805–1823. [doi:10.1103/PhysRevE.62.1805]
Treiber, M., Kesting, A., Helbing, D., 2004. Multi-anti cipative Driving in Microscopic Traffic Models. Eprint arXiv: cond-mat/0404736.
Author information
Authors and Affiliations
Additional information
Project (No. G1998030408) supported by the National Basic Research Program (973) of China
Rights and permissions
About this article
Cite this article
Li, L., Shi, Pf. Numerical analysis on car-following traffic flow models with delay time. J. Zhejiang Univ. - Sci. A 7, 204–209 (2006). https://doi.org/10.1631/jzus.2006.A0204
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1631/jzus.2006.A0204