1 Introduction

Current networks rely on rich functionalities, such as improved critical performance (e.g., proxies and load balancers), improved security (e.g., firewalls and the intrusion detection system (IDS)), reduced bandwidth costs (e.g., wide area network (WAN) optimizers), and policy compliance capabilities (e.g., network address translation (NAT) and content filters), which are introduced by a wide spectrum of specialized appliances or middleboxes (Carpenter and Brim, 2002). Sherry et al. (2012) showed that the number of middleboxes is on par with the number of routers in a network (e.g., an average very-large network holds 2850 layer-3 routers and 1946 middleboxes). In other words, middleboxes are a critical part of today’s networks and it is reasonable to expect that they will remain so in the foreseeable future (Walfish et al., 2004; Joseph and Stoica, 2008).

Though middleboxes are inevitably deployed in networks and are playing a critical role in introducing new network functionality, it is troubling that current middlebox architectures suffer from barriers, such as high cost (Anderson et al., 2012; Anwer et al., 2013), limited flexibility (Rajagopalan et al., 2013), and long development cycles (Sekar et al., 2012). The reason is that today’s middleboxes not only are closed and expensive systems with few or no hooks and application programming interfaces (APIs) for extension or experimentation, but also are built on a particular chosen hardware platform that typically supports a narrow range of specialized functions (e.g., IDS). Worse still, middleboxes are acquired from independent vendors and deployed as standalone devices with little uniformity in their management APIs or cohesiveness in how the overall middleboxes are managed (Greenberg et al., 2005).

Given the problems stated above, how to solve these issues of middleboxes has received a significant amount of attention (Hwang et al., 2015). Most recent strategies are built on two kinds of new networking technologies, namely software-defined networking (SDN) (McKeown et al., 2008; ONF, 2012; Nunes et al., 2014) and network function visualization (NFV) (Chiosi et al., 2012; Li and Chen, 2015). These technologies have emerged aiming at cost reduction, network scalability increase, and service flexibility improvement with the strategies of enabling innovation in network nodes, e.g., standardized APIs and software-centric implementations. NFV proposes to run network functions as software instances on commodity servers or datacenters, while SDN supports a decomposition of the network into control-and data-plane functions. Therefore, these new concepts are considered very promising drivers to design cost-efficient middlebox service architectures (de Turck et al., 2015; Matias et al., 2015).

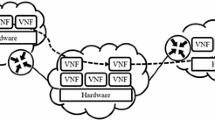
Although introducing SDN and NFV to the network function has several advantages as mentioned previously, it also brings some challenges for network transmission efficiency (Shen et al., 2015). For example, in the network shown in Fig. 1, an additional traffic transport delay is expected, which requires a thorough planning of the middlebox location within the network. In Fig. 1, two kinds of virtual middleboxes (VMs), i.e., IDS and firewall (FW), operating on general servers 1 and 2, are placed at network nodes R2 and R4. We assume that traffic 1 (red solid curve), which requires both the IDS and FW services, enters the network from border router 1 and exits the network on border router 2, while that traffic 2 (green dashed curve) needing the FW service enters the network from border router 2 and exits the network on border router 3. However, with server 1 supporting only the IDS function and server 2 performing solely the FW function, traffic 1 has to traverse the IDS box in R2 and then the FW box in R4, and traffic 2 must be steered to the FW box in server 2. Apparently, the placement scheme concerning service locations {R2, R4} increases the traffic transport delay, compared with the scheme with locations {R2, R5}.

Fig. 1
figure 1

Motivation of the service deployment problem (References to color refer to the online version of this figure)

Full size image

While routers/switches process packets at every hop, middleboxes process only packets of a subset of all the hops. Apparently, if the middleboxes are deployed randomly or in some remote nodes, the network traffic may be sent on a detour for the middle-box services, leading to a potential increase in packet latency and bandwidth consumption. Therefore, there is still an orthogonal problem at the network planning stage, i.e., where to place these middlebox services so that this performance penalty is minimized. We denote this problem as the service placement problem.

In this paper, the middlebox service placement problem is discussed, focusing on how to place services in the network with the objective of minimizing the average time it takes for the subscribers’ traffic to go through all required services. The following two key contributions are made:

  1. 1.

    We formulate the service placement problem in theory by the integer linear programming model.

  2. 2.

    We propose a heuristic solution based on the improved quantum genetic algorithm (QGA), and evaluate the algorithm performance.

2 Related work

Much current research focuses on the evolution of the middlebox service model. Generally, two complementary approaches are followed. The first tackles the high building capital expenditures (CAPEX) and limited extensibility by employing a combination of NFV and SDN. It allows operators to decouple the dependence from specialized equipment and operate network functions as virtualized software instances on a standardized platform instead. The second tackles the high operation expenditures (OPEX) and limited flexibility in the service procedure by SDN controlling routing through the specified functional sequence. The main work related to these two approaches is summarized here.

On the one hand, Sherry et al. (2012) proposed a practical service framework for outsourcing enterprise middlebox processing to the shared cloud computing platform (Qi et al., 2014). Sekar et al. (2011) innovated middlebox deployment with the software-centric middlebox implementations running on general-purpose hardware platforms managed via open and extensible management APIs. Regarding VMs as first-class entities, Gember et al. (2012a) presented a framework for immediate application deployment over or under the cloud. Furthermore, Gember et al. (2012b) realized a software-defined middlebox networking framework to simplify the management of complex and diverse functionalities. In the scenarios of NFV and SDN, Gember et al. (2014) designed a control plane called OpenNF, which could provide efficient, coordinated control of both internal middlebox state and network forwarding state.

On the other hand, Qazi et al. (2013) presented the SIMPLE architecture, an SDN-based policy enforcement layer for efficient middlebox-specific traffic steering. Built upon SDN and the OpenFlow protocol, Zhang et al. (2013) proposed a scalable framework (called StEERING) for dynamic traffic routing through any sequence of middleboxes. Fayazbakhsh et al. (2014) developed the FlowTags architecture, which consists of SDN controllers and FlowTags-enhanced middleboxes, to integrate middleboxes into SDN-capable networks. Gushchin et al. (2015) proposed a solution for routing traffic in an SDN-enabled dynamic network environment with consolidated middleboxes implemented using virtual machines. Cheng et al. (2015) used the simulating annealing algorithm for the combinational problem of service chains, which could manage network services in an efficient and scalable way.

The above studies either are based on the assumption that the service has been deployed or make only some preliminary exploration on the service problem (Basta et al., 2014; Lange et al., 2015; Mohammadkhan et al., 2015). Few studies have designed a specific deployment strategy, which is our focus in the next section.

3 Proposed solution

Our goal in this section is to address the service placement problem by combining the theory of QGA with the structure of SDN and NFV, which includes today’s SDN controller (Gude et al., 2008), OpenFlow switches, and virtual network function components. Our solution is an optimal middlebox service placement policy maker that decides a reasonable high-level deployment policy for the network.

3.1 SDN/NFV-based architecture

Fig. 2 gives an overview of our architecture, where virtual implementations of middlebox applications are consolidated to run on a general-purpose shared hardware platform, managed in a logically centralized manner with uniform APIs for a network-wide view. This SDN and NFV based solution reduces the cost and development cycles to build and deploy new middlebox applications.

Fig. 2
figure 2

Overview of middlebox deployment using SDN/NFV

Full size image

As shown in Fig. 2, the components of the architecture can be classified into three kinds: (1) the control plane components including the network operation system, decision module, and databases; (2) the data plane components containing the OpenFlow switches and VM platforms; and (3) the interfaces between the control plane and the data plane, such as the OpenFlow protocol. Next, we will describe the roles of the main components and how the proposed solution can be used in the context of SDN and NFV.

The controller is the central administrator of the network and plays a core role in our proposed scheme. The controller periodically collects network state information, including network topology, service function description, network resources (e.g., bandwidth and network-wide traffic workload), and stores them in the databases. The substrate of SDN/NFV contains routers/switches and NFV platforms, which forward the traffic and provide middlebox service. In addition, the APIs are responsible mainly for the communication tasks between the control- and data-planes.

The procedure of our placement scheme is as follows: First, with the input databases in the controller and the requirement of placement, the SDN controller runs the service placement decision module, which solves an optimization problem of minimizing network-wide transport delay. Second, the results of the decision module are output of the configuration policy to guide service placement operation by the uniform APIs. Finally, NFV platforms are placed on network nodes with optimal locations, which can provide middlebox services for the traffic from the nodes without the service placed (as illustrated by dashed lines in Fig. 2).

3.2 Integer programming model for service placement

We formulate the service deployment problem as an optimization problem that aims at minimizing the transport delay or distance to be traversed by all subscribers’ traffic (Lu et al., 2013). Assume that the network topology is defined as an undirected graph G=(V, E), with node set V representing switches and edge set E representing the links. For example, in the topology of Fig. 2, graph G is a symmetric graph with weighted edges, and each edge is associated with a transport delay value d(l) (l∈E).

The objective is to find a subset VS of the locations among all candidates V (1≤∣VS∣≤∣V∣=N, ∣ · ∣ is the cardinality of a set), and place the services in these selected locations so that the total delay for all the users is minimized. The optimization problem can be considered as an integer linear programming (ILP) model, whose feasible solution defines a scheme that satisfies our objectives. The problem is formulated as follows:

First, given two nodes v i and v j (v i , v j ∈V, v i ≡v j ), the minimum transport delay between v i and v j is calculated by

$$d({v_i},{v_j}) = \mathop {{\rm{argmin}}}\limits_{{p_k} \in P({v_i},{v_j})} \;\sum\limits_{l \in {p_k}} {d(l),} $$
((1))

where P(v i , v j ) denotes the set of paths from node v i to node v j , and p k is one path element of set P(v i , v j ).

Let D=[d(v i , v j )]N×N (i, j=1, 2, …, N) denote the shortest path matrix of graph G, and VE (VE⊂V) the egress node set. The linear optimization model is shown as

$${\rm{min}}\left( {\sum\limits_{i = 1}^N {{x_i}d({v_i},v_i^{\rm{E}}) + } \sum\limits_{i = 1}^N {(1 - {x_i})d({v_i},v_i^{\rm{S}})} } \right)$$
((2))
$$\begin{array}{*{20}c} {{\rm{s}}.{\rm{t}}.\;\forall {v_i} \in V,\;v_i^{\rm{S}} = {\rm{\{ }}{v_n}{\rm{|}}\;{v_n} \in V,{x_n} = 1,\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad } \\ {d({v_i},{v_n}) = \mathop {{\rm{argmin}}}\limits_{j = 1,2, \ldots ,N,\;{x_j} = 1} d({v_i},{v_j}){\rm{\} }},} \\ \end{array} $$
((3))
$$\begin{array}{*{20}c} {\forall {v_i} \in V,\;v_i^{\rm{E}} = {\rm{\{ }}{v_k}{\rm{|}}\;{v_k} \in {V^{\rm{E}}},\quad \quad \quad \quad \quad \quad \quad } \\ {d({v_i},{v_k}) =\arg\min\limits_{{v_j} \in {V^{\rm{E}}}} d({v_i},{v_j}){\rm{\} }},} \\ \end{array} $$
((4))
$${x_i} = {\rm{\{ }}0,\;1{\rm{\} }},\quad i = 1,2, \ldots ,N,$$
((5))

where x i ∈{0, 1} (i=1, 2, … N) are the variables of the optimization (x i =0 means that node v i is not selected for service placement; otherwise, v i is the location of the network service), \(v_i^{\rm{S}}\) is the service node corresponding to node v i , and \(v_i^{\rm{E}}\) is the egress point corresponding to node v i . Expression (2) defines the total transport delay, which is calculated as the sum of the transport delay between the ingress points and the service points and the transport delay between the service points and the egress points. Constraint (3) means assigning the service node with the minimum transport delay to v i as \(v_i^{\rm{S}}\). Constraint (4) indicates that the egress node with the minimum transport delay to v i is selected as \(v_i^{\rm{E}}\).

3.3 Solution based on the improved quantum genetic algorithm

Malossini et al. (2008) and Mohammed et al. (2012) have shown that the quantum genetic algorithm (QGA) has a good performance in dealing with integer programming. In this study, we extend the basic QGA with some improvement methods, such as dynamic rotation angle mechanism, quantum mutation, and population catastrophe. Then we propose a algorithm (called SP-IQGA) based on the improved quantum genetic algorithm (IQGA) for the ILP model to obtain the optimal service placement (SP).

3.3.1 Introduction to QGA

QGA is based on the concepts of quantum bit and quantum superposition state. The basic unit of information in quantum computation is the qubit. A qubit is a two-level quantum system with basis states ∣0〉 and ∣1〉, which can be represented by a superposition of the basis states:

$$\left| \psi \right\rangle = \alpha \left| 0 \right\rangle + \beta \left| 1 \right\rangle ,\quad {\alpha ^2} + {\beta ^2} = 1,$$
((6))

where α and β are complex numbers, denoting the probability amplitudes of the basis states.

QGA operates on a population composed of multiple feasible solutions. Each feasible solution of the QGA, which is made up of multiple qubits, is the element chromosome of the population. If the probability amplitudes of a qubit are [α, β]T, a chromosome containing N qubits is described by

$$\begin{array}{*{20}c} {{q_1}\quad {q_2}\quad \cdots \quad {q_N}} \\ {C = \left[ {\left. {\begin{array}{*{20}c} {{\alpha _1}} \\ {{\beta _1}} \\ \end{array}} \right|\left. {\begin{array}{*{20}c} {{\alpha _2}} \\ {{\beta _2}} \\ \end{array}} \right|\left. {\begin{array}{*{20}c} \cdots \\ \cdots \\ \end{array}} \right|\begin{array}{*{20}c} {{\alpha _N}} \\ {{\beta _N}} \\ \end{array}} \right],\quad \quad \quad \quad } \\ \end{array} $$
((7))

where each qubit q i (i=1, 2, …, N) of the chromosome C can be one of the state ∣0〉, state ∣1〉, and superposition of states ∣0〉 and ∣1〉, and will collapse into a certain state (∣0〉 or ∣1〉) in the observation of chromosome. So, this operation endows the QGA with better population diversity than the basic genetic algorithm.

In our SP-IQGA algorithm, the ith qubit state of chromosome C represents the service information of node v i ; i.e., q i with state ∣1〉 means that node v i is chosen as the service placement location; otherwise, q i with state ∣0〉 means that v i is not placed in the service.

3.3.2 Formulation of the SP-IQGA algorithm

The main steps of the SP-IQGA algorithm can be described as follows:

  • Step 1: acquisition of the shortest path matrix D. D is an important input parameter, and contains all minimum transport delays between any two nodes in graph G. For example, element d(v i , v j ) of the ith row and jth column in D is the minimum transport delay value between v i and v j , which can be calculated by using the Bellman-Ford algorithm.

  • Step 2: initialization of the QGA. At the initial stage of SP-IQGA, we set the chromosome population size as M and the qubit length of each individual chromosome as N. Denote the tth generation population as \(P(t) = {\rm{\{ }}C_1^{(t)},C_2^{(t)}, \ldots ,C_M^{(t)}{\rm{\} }}\), where \(C_m^{(t)}\) (m=1, 2, …, M) is as described in Eq. (7). In the initial search of the algorithm, all states appear with the same probability, so we set

    $$\alpha _{mi}^{(0)} = \beta _{mi}^{(0)} = {1 \over {\sqrt 2 }},\quad i = 1,2, \ldots ,N,\;\;m = 1,2, \ldots ,M,$$

    and obtain

    $$\begin{array}{*{20}c} {C_m^{(0)}} & { = \left[ {\left. {\begin{array}{*{20}c} {\alpha _{m1}^{(0)}} \\ {\beta _{m1}^{(0)}} \\ \end{array}} \right|\left. {\begin{array}{*{20}c} {\alpha _{m2}^{(0)}} \\ {\beta _{m2}^{(0)}} \\ \end{array}} \right|\left. {\begin{array}{*{20}c} \cdots \\ \cdots \\ \end{array}} \right|\begin{array}{*{20}c} {\alpha _{mN}^{(0)}} \\ {\beta _{mN}^{(0)}} \\ \end{array}} \right]\quad \quad \;} \\ {} & { = \left[ {\left. {\begin{array}{*{20}c} {1/\sqrt 2 } \\ {1/\sqrt 2 } \\ \end{array}} \right|\left. {\begin{array}{*{20}c} {1/\sqrt 2 } \\ {1/\sqrt 2 } \\ \end{array}} \right|\left. {\begin{array}{*{20}c} \cdots \\ \cdots \\ \end{array}} \right|\begin{array}{*{20}c} {1/\sqrt 2 } \\ {1/\sqrt 2 } \\ \end{array}} \right].} \\ \end{array} $$

  • Step 3: measurement of the observation value of chromosome C. The chromosome observation is to make each qubit of the chromosome collapse into a certain state. The measurement method is to generate a random number in range [0, 1] for each qubit. If the random number is less than ∣α∣2, the measurement value of the qubit is 0; otherwise, it is 1. After the measurement operation, C is transformed to the observation value X C ={x1, x2, …, x N }, where x i (i=1, 2, …, N) is a binary variable (0 or 1).

  • Step 4: calculation of the fitness. The fitness is the metric indicating the quality of the individual. The higher the fitness value, the closer the individual to the optimal solution. For individual X C ={x1, x2, x N }, the fitness function can be obtained by

    $${\rm{Fit}}({X_C}) = {\left[ {\sum\limits_{i - 1}^N {{x_i}d({v_i},v_i^{\rm{E}}) + } \sum\limits_{i = 1}^N {(1 - {x_i})d({v_i},v_i^{\rm{S}})} } \right]^{ - 1}}.$$
    ((8))

  • Step 5: adaptive adjustment strategy for the quantum rotation gate. In QGA, the population can be updated by quantum rotation gate U(θ). Based on the quantum rotation gate, the adjustment operation of the ith qubit in \(C_m^{(t)}\) is as follows:

    $$\left[ {\begin{array}{*{20}c} {\alpha _{mi}^\prime} \\ {\beta _{mi}^\prime} \\ \end{array}} \right] = U(\theta )\left[ {\begin{array}{*{20}c} {{\alpha _{mi}}} \\ {{\beta _{mi}}} \\ \end{array}} \right] = \left[ {\begin{array}{*{20}c} {{\rm{cos}}\;{\theta _i}} & { - {\rm{sin}}\;{\theta _i}} \\ {{\rm{sin}}\;{\theta _i}} & {{\rm{cos}}\;{\theta _i}} \\ \end{array}} \right]\;\left[ {\begin{array}{*{20}c} {{\alpha _{mi}}} \\ {{\beta _{mi}}} \\ \end{array}} \right],$$
    ((9))

    where \({\alpha'_{mi}}\) and \({\beta'_{mi}}\) represent the probability amplitudes of the ith qubit after adjustment. θ i denotes the rotation angle of quantum rotation gate, defined by

    $${\theta _i} = S({\alpha _i},{\beta _i}) \cdot \Delta {\theta _i},$$
    ((10))

    where s(α i , β i ) determines the direction of quantum rotation and Δθ i determines the size of quantum rotation. To reduce the influence of the rotation angle on the algorithm convergence rate, an adaptive method is used to adjust θ i in this study. Specific adjustment policies are shown in Table 1, where δ is a coefficient related to the convergence rate of the algorithm, and we set it as a variable changing with the number of iterations:

    $$\delta = 0.04\pi \left( {1 - \sigma \cdot {t \over {T + 1}}} \right),$$
    ((11))

    where σ∈[0, 1] is a constant, t is the current evolution iteration number, and T is the total number of evolution iterations.

  • Step 6: quantum variation and quantum crossover. The performance of QGA can be improved by quantum variation and quantum crossover. Quantum variation can generate new individuals to prevent QGA from evolving into a local optimal solution. During the variation, we choose a small proportion of individuals from the population, appoint randomly a variable qubit of chromosomes, and swap the probability amplitudes α and β of the appointed qubit. On the other hand, quantum crossover can produce more new models to improve the searching performance of the algorithm. Our specific implementation process is that all individuals in the population are ordered randomly and then a new population is obtained by cyclically shifting the ith qubit for i−1 times in all ordered individuals.

    Table 1 Adjustment policies for the rotation angle
    Full size table

Based on the above description, we input all algorithm parameters and call the SP-IQGA algorithm to obtain the service placement scheme. The process flow is shown in Algorithm 1.

Upon the controller, the decision module runs the SP-IQGA algorithm and achieves the result Xb={x1, x2, …, x i , …, x N }, where x i represents the node v i being the service location vS.

4 Performance evaluation

4.1 Experimental environment

To evaluate the performance, we set up the experimental environment on a computer with a 2.67 GHz two-core Intel® Core™ i7 CPU and 4 GB RAM. The GT-ITM tool (Zegura et al., 1996) is used for generating different network topologies, and we implement the proposed algorithm with MATLAB.

We evaluate the SP-IQGA algorithm for the service location described in Section 3 using the test topology from the GT-ITM and the simulated real network traffic from the data center network traffic record. The method for generating links is Waxman, with parameters α=0.3 and β=0.2. The link transport delay in the test topology is measured in millisecond, and the transport delay of each link is randomly distributed in range [1, 100]. In SP-IQGA, we set the population size M=20 and the variation probability r=0.1.

4.2 Evaluation results

4.2.1 Effectiveness of different parameters

With the intelligent decision of QGA, SP-IQGA can calculate automatically the service node number (NS) under different network topologies. For different network sizes (NV), the optimal service node ratios (NS/NV) with different numbers of egress nodes (NE) are obtained by SP-IQGA (Eqs. (2)–(5)) (Fig. 3). It is intuitive to find that the service node ratio is in range [0.05, 0.25] and increases with NE. The reason is that with more egress nodes, more network nodes become suitable for the placing service.

Fig. 3
figure 3

Service node ratio with different network sizes

Full size image

Then, under different values of parameter NE and set NV=100, we show the overall transport delay (Eq. (2)) of network traffic varying with the iteration number in Fig. 4. SP-IQGA reaches rapidly the convergence state after about 100 iterations and searches toward the optimal solution by quantum variation and quantum crossover (i.e., sharp changes in the overall delays).

Fig. 4
figure 4

Overall transport delay with different number of iterations

Full size image

Finally, we test the convergence performance of SP-IQGA by comparison with the genetic algorithm (GA) and the basic quantum genetic algorithm (QGA). Under the conditions NE=5 and NV=200 or 500, we acquire the simulation results of three algorithms. Fig. 5 illustrates that our SP-IQGA converges to the stable states faster. Furthermore, the larger the network size, the more obvious the advantage.

Fig. 5
figure 5

Convergence comparison of different strategies

Full size image

Furthermore, we show the time consumptions of operating 200 iterations for the three algorithms in Fig. 6. As shown, with the increase in network size, the computation time of the three methods also increases rapidly. The consumed time of SP-IQGA is more than that of QGA, and both are much higher than that of GA. The reason is that SP-IQGA and QGA execute quantum operation, quantum variation, and quantum crossover, which spend more calculation time. In particular, the dynamic quantum rotation operation in the SP-IQGA algorithm further increases its time consumption.

Fig. 6
figure 6

Comparison of time cost of different strategies

Full size image

4.2.2 Comparison of different algorithms

To verify the performance of the proposed algorithm, we compare our SP-IQGA with four other placement strategies.

Strategy 1 is based on random placement, denoted as SP-Random; strategy 2 is based on the greedy algorithm, denoted as SP-Greedy (Zhang et al., 2013); strategy 3 is based on a heuristics, denoted as SP-B+COR (Mohammadkhan et al., 2015); strategy 4 is based on another heuristics, denoted as SP-Anneal (Cheng et al., 2015). The notations and descriptions of different algorithms are listed in Table 2.

Table 2 Comparison of algorithms
Full size table

Fig. 7 shows the simulation results of the five strategies when NE=5. The overall transport delay of the optimal deployment scheme obtained by different policies increases with the increase of the network size. It is easily seen that the transport delay of SP-IQGA is similar to that of SP-B+COR, and they are both lower than that of the three other strategies under the same network size.

Fig. 7
figure 7

Comparison of overall transport delay under different network sizes

Full size image

Under the same condition as in Fig. 7, Fig. 8 shows the computational time overhead of the five algorithms. Because the random strategy does not need to solve the optimization problem, its time overhead is set to zero. The simulation results demonstrate that the calculation time of SP-B+COR is the highest among the algorithms compared and its time consumption increases rapidly with the increase of the network size. Relatively speaking, the calculation time overhead of our proposed SP-IQGA algorithm is significantly lower than that of the three other heuristic algorithms, and it is less affected by the network size.

Fig. 8
figure 8

Comparison of time cost of different algorithms under different network sizes

Full size image

For the network topology with NV=100 and NE=5, we execute service placement using the five algorithms to obtain their respective optimal deployment schemes: Xrandom, Xgreedy, Xanneal, XB+COR, and XIQGA. We simulate 10 types of application traffics and each application contains 5 data flows. Therefore, a total number of 50 flows are investigated. Suppose that every data flow needs to be processed by middlebox services, and these service requests can be satisfied by a service node. Under the five service placement schemes, we let all flows transport the network topology and compute the average transport delay of each traffic for different deployment schemes.

Fig. 9 shows the average transport delay of data flows in each network application under different placement algorithms. The results show that the average transport delay of SP-Random is the highest among all schemes. The delays of SP-Greedy and SP-Anneal are similar and lie in the middle of the algorithms compared. SP-B+COR and SP-IQGA can achieve less transport delay.

Fig. 9
figure 9

Comparison of average transport delay under different traffic flows

Full size image

Fig. 10 shows the transport delay cumulative distribution function (CDF) for all the flows. CDF can show clearly the transmission delay distribution of all applications. The greater the curvature of a CDF curve, the more concentrated the delay value distribution. As shown, the transport delay of each data flow is distributed in [0, 200]. For 50% of the flows, SP-B+COR and SP-IQGA can achieve about 51 and 55 ms transport delays, respectively, while SP-Greedy, SP-Anneal, and SP-Random need 63, 67, and 80 ms transport delays, respectively. Compared with SP-Random, SP-IQGA can decrease the transport delay by about 30%. Thus, the advantage of SP-IQGA is significant, and it can be used to efficiently solve the service placement problem.

Fig. 10
figure 10

Distribution of transport delay of different service placement strategies

Full size image

5 Conclusions

To solve the service deployment problem in the NFV and SDN network environment, we presented a placement approach based on the improved quantum genetic algorithm. Built on top of SDN and the intelligence of QGA, our placement strategy can automatically obtain the optimal schemes for different network topologies. Simulation experiments showed that significant latency reduction can be obtained by our algorithm for placing services in different network topologies. In future work, we will use the proposed approach to help construct network function service chains.