Skip to main content
SpringerLink
Log in

Selecting creep models using Bayesian methods

  • Original Article
  • Published:
Materials and Structures Aims and scope Submit manuscript

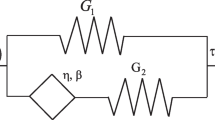
Abstract

The development of creep prediction models has been a field of extensive research and many different models have already been proposed. This paper presents an evaluation method of the prediction quality of creep models for specific experimental data. Within the scope of this paper, the model according to Bockhold and the model according to Heidolf are examined. First, the parameters of the models are identified with respect to existing experimental data. This is done using a sampling based approach of Bayesian updating developed by Bažant and Chern. In extension to the method by Bažant and Chern, the uncertainty coming from inaccurate measurement data is taken into account in the definition of the likelihood function within the updating algorithm. The more inaccurate the measurements are, the more uncertain the estimated model parameters and model prognoses become. The identification is performed for different short- and long-term creep tests. The intension is not to validate these models intensively, but to evaluate their prognoses for the individually tested creep behavior. The results show that the identifiability of the models’ parameters is different for both models and consequently the models prognoses differ in their uncertainties. Second, the models are evaluated using two different strategies: the stochastic model selection according to MacKay, Beck and Yuen based on the Ockham factor, and a comparison of the uncertainties taking into account parameter and model uncertainties. The results of the evaluation of the creep models differ for various experimental tests. Model Heidolf is more flexible and gives a better fit to the data, however, it fails to predict reliable long-term creep deformations using only short-term measurements compared to model Bockhold. Comparing the evaluation methods, the analysis of uncertainties of the creep prognosis proofs to be more stable than the evaluation using the stochastic model selection.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13

Similar content being viewed by others

Abbreviations

\(\alpha_{\rm c,cr}^{i}\) :

History variable of maximum stress (MN/m2)

αc,v-el, αc,v-pl :

Creep non-linearity functions of stiffness, model Heidolf (–)

\(a_{\text{c,v-el}}^{i,l}, a_{\text{c,v-pl}}^{j,l}\) :

Polynomial factors of creep non-linearity functions, model Heidolf (–)

b :

Parameter to distinguish \(\varepsilon_{\rm c,cr,in}\) in \(\varepsilon_{\rm c,cr,pl}\) and \(\varepsilon_{\rm c,cr,da}\) (–)

c0, c1 :

Normalizing constants

C cr,meas, C cr,model :

Creep compliance of measurements and model (m2/MN)

C i,j , COV:

Covariance matrix

CV:

Coefficient of variation (–)

CVmodel :

Coefficient of variation of model prognosis to measurements (–)

d :

Index for damper

\(D_{\rm c,cr}^{i}\) :

Damage parameter (–)

\(E \left[\ldots\right]\) :

Expected value

E c, E c,0 :

Young’s modulus, Young’s modulus at t 0 (MN/m2)

\(E_{\text{c,v-el}}^{i}, E_{\text{c,v-pl}}^{j}\) :

Stiffness of spring of Kelvin/Bingham-chain, model Heidolf (MN/m2)

\(e_{\rm d}, \varepsilon_{{\rm c},0}, g_{\rm d}\) :

Parameters of time invariant concrete model of Häußler-Combe [1] (–)

\(\eta_{\rm c}\) :

Viscosity of damper (MNdays/m2)

\(\varepsilon_{\rm c,el}, \varepsilon_{\rm c,pl}, \varepsilon_{\rm c,da}\) :

Short-term strains of concrete: elastic, plastic, damage (–)

\(\varepsilon_{\rm c,cr}, \dot{\varepsilon}_{\rm c,cr}, \ddot{\varepsilon}_{\rm c,cr}\) :

Creep strains, creep rate, creep acceleration, (–), (1/days), (1/days2)

\(\varepsilon_{\text{c,cr,v-el}}, \varepsilon_{\text{c,cr,v-pl}}\) :

Long-term strains of concrete: visco-elastic and visco-plastic (–)

\(\varepsilon_{\rm c,cr,el}, \varepsilon_{\rm c,cr,in}, \varepsilon_{\rm c,cr,pl}, \varepsilon_{\rm c,cr,da}\) :

Creep strains of concrete: elastic, inelastic, plastic and damage (–)

\(\varepsilon_{\rm c1}\) :

Concrete strain at concrete strength (–)

f c, f c,0 :

Short-term concrete strength, short-term concrete strength at t 0 (MN/m2)

f c,T , f c,T,0 :

Long-term concrete strength, long-term concrete strength at t 0 (MN/m2)

H :

Hessian matrix

i :

ith creep chain of model Bockhold

i, j :

ith Kelvin- and j-th Bingham-chain of model Heidolf

k :

Actual sample

K :

Number of samples

L :

Order of creep non-linearity functions of stiffness, model Heidolf

\(L\left(A|B\right)\) :

Likelihood of A under condition of B

m :

Number of creep chains, model Bockhold

m, n :

Number of Kelvin/Bingham-chains, model Heidolf

m :

Measurement point

M :

Number of measurement points

M j :

Model class j

n :

Exponent of damper non-linearity, model Bockhold (–)

n :

Number of actual time increment

N M :

Number of model classes in model group U

\(p\left(A\right)\) :

Probability density function of A

\(p\left(A|B\right)\) :

Probability density function of A under condition of B

\(P\left(A\right)\) :

Probability of A (–)

\(P\left(A|B\right)\) :

Conditional probability of A under condition of B (–)

\(P^{\prime}\left(A\right)\) :

Prior probability of A (–)

\(P^{\prime\prime}\left(A\right)\) :

Posterior (updated) probability of A (–)

s :

Index for spring

τ:

Time at the beginning of actual time increment (days)

\(\tau_{\rm c}^{i}, \tau_{\text{c,v-el}}^{i}, \tau_{\text{c,v-pl}}^{j}\) :

Retardation time of dampers (days)

\(\Updelta t\) :

Time step (days)

t, t 0, t unl. :

Actual time, time at beginning of loading, time at unloading (days)

\({\varvec{\theta}}\) :

Parameter vector

\({\varvec{\theta}}^{k}\) :

Parameter vector of sample k

\(\sigma_{\rm c}, \sigma_{\rm c,s}^{i}, \sigma_{\rm c,d}^{i}\) :

Concrete stress, stress of spring, stress of damper (MN/m2)

\(\sigma_{\bullet}\) :

Standard deviation of •

\(\sigma_{X_{m}}\) :

Standard deviation of measurements

U :

Group of available models

X m :

Measurement data at measurement point m

\(\Uppsi\) :

Model uncertainty factor (–)

\(\overline{\bullet}\) :

Mean values of •

\(\hat{\bullet}\) :

Optimal value of •

References

  1. Häußler-Combe U, Pröchtel P (2005) Ein dreiaxiales Stoffgesetz für Betone mit normaler und hoher Festigkeit. Beton- und Stahlbetonbau 100(1):52–62

    Article  Google Scholar 

  2. Box GEP, Tiao GC (1992) Bayesian inference in statistical analysis. Wiley, New York

  3. Donaldson JR, Schnabel RB (1985) Computational experience with confidence regions and confidence intervals for nonlinear least squares. Technical report. University of Colorado at Boulder

  4. Ledesma A, Gens A, Alonso EE (1996) Estimation of parameters in geotechnical backanalysis. I. Maximum likelihood approach. Comput Geotech 18(1):1–27

    Article  Google Scholar 

  5. Most T (2010) Identification of the parameter of complex constitutive models: least squares minimization vs. Bayesian updating. In: IFIP WG 7.5 working conference on reliability and optimization of structural systems

  6. Berveiller M, Le Pape Y, Sudret B, Perrin F (2007) Bayesian updating of the long-term creep strains in concrete containment vessels using a non intrusive stochastic finite element method. In: Kanda J, Takada T, Furuta H (eds) Applications of statistics and probability in civil engineering. Taylor & Francis. ISBN 978-0-415-45211-3

  7. Yang IH (2007) Prediction of time-dependent effects in concrete structures using early measurement data. Eng Struct 29:2701–2710

    Article  Google Scholar 

  8. Mwanza P, Scanlon A (2000) Bayesian prediction of prestress loss in prestressed concrete bridge girders. In: 8th ASCE specialty conference on probabilistic mechanics and structural reliability

  9. Bažant ZP, Kim J-K (1989) Segmental box girder: deflection probability and Bayesian updating. J Struct Eng 115(10):2528–2547

    Article  Google Scholar 

  10. Yuen K-V, Katafygiotis LS (2002) Bayesian modal updating using complete input and incomplete response noisy measurements. J Eng Mech 128(3):340–350

    Article  Google Scholar 

  11. Wu JR, Li QS (2006) Structural parameter identification and damage detection for a steel structure using a two-stage finite element model updating method. J Constr Steel Res 62:231–239

    Article  Google Scholar 

  12. Conte JP, Moaveni B, He X, Barbosa AR (2007) System and damage identification of a seven-story reinforced concrete building structure tested on the UCSD-NEES shake table. In: Proceeding of international conference on experimental vibration analysis for civil engineering structures

  13. Gardner NJ (2004) Comparison of prediction provisions for drying shrinkage and creep of normal-strength concretes. Can J Civil Eng 31:767–775

    Article  Google Scholar 

  14. Al-Manaseer A, Lam J-P (2005) Statistical evaluation of shrinkage and creep models. ACI Mater J 102(3):170–176

    Google Scholar 

  15. Bažant ZP, Li G-H (2008) Unbiased statistical comparison of creep and shrinkage prediction models. ACI Mater J 105(6):610–621

    Google Scholar 

  16. Yang IH (2005) Uncertainty and updating of long-term prediction of prestress forces in PSC box girder bridges. Comput Struct 83:2137–2149

    Article  Google Scholar 

  17. Keitel H, Dimmig-Osburg A (2010) Uncertainty and sensitivity analysis of creep models for uncorrelated and correlated input parameters. Eng Struct 32(11):3758–3767

    Article  Google Scholar 

  18. Bockhold J (2005) Modellbildung und numerische Analyse nichtlinearer Kriechprozesse in Stahlbetonkonstruktionen unter Schädigungsaspekten. Dissertation, Ruhr-Universität Bochum

  19. Bockhold J (2007) 3D material model for nonlinear basic creep of concrete. Comput Concr 4(2):101–117

    Google Scholar 

  20. Pölling R (2000) Eine praxisnahe, schädigungsorientierte Materialbeschreibung von Stahlbeton für Strukturanalysen. Dissertation, Ruhr-Universität Bochum

  21. Comite Euro-International du Beton (CEB) (1993) CEB–FIP Model Code 1990. Technical report. Comite Euro-International du Beton

  22. Nechvatal D (1996) Normalbeton unter hohen Dauerlasten bei verhindertem Feuchteaustausch. Dissertation, Technische Universität München

  23. Pfister R (2007) Ein Ermüdigungsschädigungmodell für Zuverlässigkeitsanalysen von Stahlbetontragwerken. Dissertation, Ruhr-Universität Bochum

  24. Heidolf T (2007) Zeit- und beanspruchungsabhängiges Tragverhalten von polymermodifiziertem Beton unter mehrfach wiederholter Beanspruchung. Dissertation, Bauhaus-Universität Weimar

  25. Heidolf T (2009) Zeitvariantes Trag- und Schädigungsverhalten von mehrfach wiederholt beanspruchtem polymermodifizierten Beton (PCC), Teil 2: Modellbildung zum Tragverhalten von Beton. Beton- und Stahlbetonbau 104(12):823–834

    Article  Google Scholar 

  26. Bažant ZP, Bajewa S (1995) Creep and shrinkage prediction model for analysis and design of concrete structures—model B3. Mater Struct 28:357–365

    Article  Google Scholar 

  27. Shen J-H (1992) Lineare und nichtlineare Theorie des Kriechens und der Relaxation von Beton unter Druckbeanspruchung. In: Deutscher Ausschuss für Stahlbeton—Heft 432. Beuth Verlag GmbH

  28. Bažant ZP, Chern J-C (1984) Bayesian statistical prediction of concrete creep and shrinkage. ACI Mater J 81:319–330

    Google Scholar 

  29. Iman RL, Conover WJ (1980) Small sample sensitivity analysis techniques for computer models with an application to risk assessment. Commun Stat A9(17):1749–1842

    MathSciNet  MATH  Google Scholar 

  30. Bažant ZP (1985) Probabilistic analysis of creep effects in concrete structures. In: Proceedings of 4th international conference on structural safety and reliability, pp I-331–I-334

  31. Bažant ZP, Kim JK, Wittmann FH, Alou F (1987) Statistical extrapolation of shrinkage data. Part II. Bayesian updating. ACI Mater J 84:83–91

    Google Scholar 

  32. Hastings WK (1970) Monte Carlo sampling methods using Markov chains and their application. Biometrika 57:97–109

    Article  MATH  Google Scholar 

  33. Chib S, Greenberg E (1995) Understanding the Metropolis–Hastings algorithm. Am Stat 49(4):327–335

    Google Scholar 

  34. Vrouwenvelder T (2002) Probabilistic model code, 12th draft. Technical report. Joint Committee on Structural Safety

  35. Vismann U (1995) Zuverlässigkeitstheoretische Verifikation von Bemessungskriterien im Stahlbetonbau. Dissertation, Technische Universität München

  36. Bažant ZP, Bajewa S (1995) Justificaton and refinements of model B3 for concrete creep and shrinkage. 1. Statistics and sensitivity. Mater Struct 28:415–430

    Article  Google Scholar 

  37. Heirman G, Vandewalle L, Van Gemert D, Boel V, Audenaert K, De Schutter G, Desmet B, Vantomme J (2008) Time-dependent deformations of limestone powder type self-compacting concrete. Eng Struct 30:2945–2956

    Article  Google Scholar 

  38. Madsen HO, Bažant ZP (1983) Uncertainty analysis of creep and shrinkage effects in concrete structures. ACI J 80B:116–127

    Google Scholar 

  39. Rostasy FS, Teichen K-H, Engelke H (1973) Beitrag zur Klärung des Zusammenhangs von Kriechen und Relaxation bei Normalbeton. Technical report. Otto-Graf-Institut—Amtliche Forschungs- und Materialprüfanstalt für das Bauwesen—Universität Stuttgart

  40. Müller HS. RILEM Data Bank, provided by Dr. H. S. Müller. Universität Karlsruhe (th), Institut für Massivbau und Baustofftechnologie, Abteilung Baustofftechnologie, Karlsruhe

  41. MacKay DJC (1992) Bayesian interpolation. Neural Comput 4:415–447

    Article  Google Scholar 

  42. Beck JL, Yuen K-V (2004) Model selection using response measurements: Bayesian probabilistic approach. J Eng Mech 130(2):192–203

    Article  Google Scholar 

  43. Gull SF (1988) Bayesian inductive inference and maximum entropy. In: Erickson GJ, Smith CR (eds) Maximum entropy and Bayesian methods in science and engineering, vol 1: foundations. Kluwer

  44. Akaike H (1974) A new Look at the Statistical Model Identification. IEEE Trans Autom Control 19(6):716–723

    Article  MathSciNet  MATH  Google Scholar 

  45. Schwarz GE (1978) Estimating the dimension of a model. Ann Stat 6(2):461–464

    Article  MATH  Google Scholar 

Download references

Acknowledgments

This author gratefully acknowledges the support for this research, provided by the German Research Foundation (DFG) through the Research Training Group 1462.

Author information

Authors and Affiliations

  1. Research Training Group 1462, Bauhaus-Universität Weimar, Berkaer Str. 9, 99423, Weimar, Germany

    Holger Keitel

  2. Department of Civil Engineering - Chair of Polymer Materials, Bauhaus-Universität Weimar, Coudraystr. 11a, 99423, Weimar, Germany

    Andrea Dimmig-Osburg

  3. Department of Civil Engineering - Building Materials and Building Technology Section, Katholieke Universiteit Leuven, Kasteelpark Arenberg 40, 3001, Heverlee, Belgium

    Lucie Vandewalle & Luc Schueremans

Authors
  1. Holger Keitel
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Andrea Dimmig-Osburg
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Lucie Vandewalle
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Luc Schueremans
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Holger Keitel.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Keitel, H., Dimmig-Osburg, A., Vandewalle, L. et al. Selecting creep models using Bayesian methods. Mater Struct 45, 1513–1533 (2012). https://doi.org/10.1617/s11527-012-9854-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1617/s11527-012-9854-x

Keywords

Search

Navigation