1 Introduction

The deterioration of porous building materials and structures by the crystallization of water soluble salts is a well known phenomenon. The threats posed by salts to porous materials can be minimized either by controlling the environment or by removing the salts from the zone of deterioration. In the case of porous building materials salt extraction is typically accomplished by dry removal of the salt efflorescence and/or aqueous methods—a common example of which being the use of poultices [1–3] to reduce salt content of the affected object. The extraction efficiency of a poultice is largely limited by the permeability and pore size distribution of both the poultice and the substrate [4, 5]. Since the pore size distribution of a poultice can vary with its moisture content mainly due to its shrinkage during drying [5], it is difficult to tailor the pore size distribution of a poultice precisely to those required for optimum salt extraction efficiency. Also, the effective depth of salt extraction achieved using poultices in the case of building materials is often low, e.g. for fired-clay brick it is of the order of 20 mm [2]. Diurnal fluctuations in temperature and relative humidity are additional factors that can significantly affect the performance of a poultice [2]. It has been proposed that the limitations posed by poultices can be overcome by using electrokinetics as an alternative desalination method for brick masonry [6].

The electrokinetic method aims to remove ionic species from the zone of deterioration by an externally applied electric field. Although the electrokinetic technique has already been used to decontaminate soil [7] and concrete [8], its application in the desalination and dehumidification of masonry bricks and walls is a recent topic [6, 9–12]. During the electrokinetic desalination of masonry bricks, electromigration of salt ions is considered the dominant transport mechanism and the contribution of both diffusion and advection transport processes is usually neglected. In this study the effects of both diffusion and advection in addition to electromigration on the transport of salt ions through fired-clay bricks under an applied electric field are also considered.

Until now, the effect of electrokinetic desalination has been investigated using destructive methods. These methods are limited by their inability to measure variations in moisture and salt content in porous media during the salt extraction process. Moreover, the spatial resolution is restricted (being generally in the order of 10 mm). Consequently, for this study non destructive measurements were performed during the electrokinetic desalination of building materials by using Nuclear magnetic resonance (NMR). It has been shown that NMR is a powerful technique for measuring the combined transport of moisture and Na ions in the building materials [13].

The objective of this work is to measure the contribution of diffusion, advection and electromigration to the overall salt transport under the influence of concentration, hydraulic and potential gradients respectively.

2 Transport processes during electrokinetic desalination

During electrokinetic desalination an applied electric field is used to mobilize salt ions from the depth of the porous material towards its surface. The removal of salt ions from the material’s surface is then typically accomplished using aqueous poulticing methods. For this purpose during electrokinetic desalination poultices in the form of wet sorbent materials (e.g. sponges, clays etc.) are applied to the surface of the porous material together with the electrodes. However, the migration of salt ions towards the surface of the porous material and the applied poultice establish a concentration gradient within the material, and thereby can induce ion diffusion. Moreover, salt can also be transported by hydraulic gradients, caused by any difference in water level across the specimen. Finally, evaporative drying of the initially wet sorbent materials can also result in salt transport due to capillary advection.

A brief description of each of the transport processes (diffusion, advection, electromigration), in saturated porous media, relevant to this study is given below.

2.1 Diffusion

The transport of ions under the influence of a concentration gradient is known as diffusion. The flux of dissolved ions in free solutions can be described by the Fick’s first law (see e.g. [14]):

$$ J_{\text{d}} = D\frac{\partial C}{\partial x} $$
(1)

where J d (mol m−2 s−1) is the flux of ions due to diffusion, C (mol l−1) is the molar concentration, D (m2 s−1) is diffusion coefficient of ionic species and x (m) is the distance.

In porous materials the salt ions cannot diffuse freely and their diffusion rates are restricted by the porosity and tortuosity of the material. In addition, the chemical or electrical interaction of the material with the pore solution can also affect the diffusion rates. For non reactive porous materials the diffusion can be described by:

$$ J_{\text{d}} = D_{\text{eff}} \frac{\partial C}{\partial x}, $$
(2)

where D eff (m2 s−1) is the effective diffusion coefficient for a given non reactive porous material. For a porous material this effective diffusion coefficient is given by:

$$ D_{\text{eff}} = \phi {T^{*}}D, $$
(3)

where ϕ (m3 m−3) is the porosity and T* is the tortuosity of the porous material. For many porous building materials, the diffusion coefficient is in the order of 0.1–1 × 10−9 m2 s−1 [15].

2.2 Advection

In porous media advection refers to the transport of salt ions under the influence of a pressure gradient. The volumetric flux or Darcy velocity v h (m s−1) of a fluid through a porous medium due to a hydraulic gradient is given by Darcy’s law (see e.g. [16]:

$$ v_{\text{h}} = \frac{k}{\eta }\frac{\partial P}{\partial x} $$
(4)

where k (m2) is the intrinsic permeability of the porous material, P (Pa) is the pressure across the porous material, and η (Pa s) is the dynamic viscosity of the fluid.

If we neglect hydraulic dispersion effects, the flux of salt ions contained within the pore fluid i.e. the movement of solute through a porous material due to a hydraulic gradient is given by:

$$ J_{\text{h}} = Cv_{\text{h}} , $$
(5)

where J h (mol m−2 s−1) is the flux of ions through the porous material and C (mol l−1) is the molar concentration of ions in the pore solution. The permeability of clay bricks lies in the region of 10−12–10−16 m2 [16, 17].

2.3 Electromigration

When a potential difference is applied across an electrolytic solution the movement of salt ions induced in response to the electric field is known as electromigration. During electromigration the flux of salt ions through bulk solution is given by Atkins and de Paula [14]:

$$ J_{\text{m}} = \mu C\frac{\partial V}{\partial x}, $$
(6)

where J m (mol m−2 s−1) is the flux of salt ions due to electromigration, μ (m2 s−1 V−1) is the mobility of ions in the electrolyte solution, C (mol l−1) is the molar concentration, V (V) is the applied voltage across the salt solution, and x (m) is the distance between electrodes.

Contrary to the case in bulk solutions, aqueous ions in porous materials are not able to move directly to the corresponding electrode by the shortest route. Instead, their movement is restricted by the porosity and tortuosity of the material. Hence, for a porous material the electromigration can be described by:

$$ J_{\text{m}} = \mu_{\text{eff}} C\frac{\partial V}{\partial x}, $$
(7)

where μ eff (m2 s−1 V−1) is the effective mobility of a particular ion for a given porous material and is given by:

$$ \mu_{\text{eff}} = \phi {T^{*}}\mu , $$
(8)

where ϕ (m3 m−3) is the porosity and T* is the tortuosity of the material.

In porous materials the effective ionic mobility μ eff is usually estimated by using the Nernst–Townsend–Einstein relation [18]:

$$ \mu_{\text{eff}} = \frac{{D_{\text{eff}} ZF}}{RT}, $$
(9)

where D eff (m2 s−1) is the effective diffusion coefficient of a particular ion for a given porous material, Z is the charge number, F (C mol−1) is the Faraday constant, R (J K−1 mol−1) is the ideal gas constant, and T (K) is the absolute temperature.

The applied electric field does not only promote the movement of salt ions through the porous material but it also produces new ionic species at the boundaries of the material due to electrochemical reactions at the electrodes. In the case of inert electrodes the following reactions take place:

$$ \left( {\text{Anode side}} \right)\quad 2{\text{H}}_{2} {\text{O}} - 4e^{ - } \to 4{\text{H}}^{ + } + {\text{O}}_{2} $$
(10)
$$ \left( {\text{Cathode side}} \right)\quad 2{\text{H}}_{2} {\text{O}} + 2e^{ - } \to 2{\text{OH}}^{ - } + {\text{H}}_{2} $$
(11)

The relatively higher diffusion coefficients and effective mobilities of hydrogen H+ and hydroxyl OH− ions [18] and an increase in their concentration with time can result in lowering the transference number of salt ions and consequently limiting their transport in porous materials. Such a decrease in the transference number of chloride ions under the influence of OH− ions has been observed during their electrochemical removal from the concrete [19]. Moreover, in the case of pH sensitive materials the acidic environment around the anode in particular can cause damage.

2.4 Total mass flux

The total mass flux of ions through a porous material under the combined effect of diffusion, advection and electromigration, J, is given by adding together their respective fluxes [20]:

$$ J = D_{\text{eff}} \frac{\partial C}{\partial x} + Cv_{\text{h}} + \mu_{\text{eff}} C\frac{\partial V}{\partial x} $$
(12)

The variation in concentration of salt ions with time is obtained by using the law of conservation of mass:

$$ \frac{\partial C}{\partial t} = - \nabla J $$
(13)

Hence by combining Eqs. 12 and 13, the variation in concentration is given by:

$$ \frac{\partial C}{\partial t} = D_{\text{eff}} \frac{{\partial^{2} C}}{{\partial x^{2} }} - v_{\text{h}} \frac{\partial C}{\partial x} - \mu_{\text{eff}} \frac{\partial C}{\partial x}\frac{\partial V}{\partial x} $$
(14)

Here we have assumed that D eff is independent of salt concentration, v h is uniform and the variation in electric field (i.e. \( ({{\partial V} \mathord{\left/ {\vphantom {{\partial V} {\partial x}}} \right. \kern-\nulldelimiterspace} {\partial x}}) \)) is linear across the specimen.

3 Experimental

In order to study the variation in moisture and salt concentration within the brick specimen under the effect of diffusion, advection and electromigration two types of sample holders were designed to be used in the NMR set-up. The detail of both the electrokinetic and NMR set-ups is given below.

3.1 Electrokinetic set-up

To obtain information regarding the variation in moisture and salt concentration in the salt contaminated brick specimen during the experiments, two types of sample holders were designed (see in Fig. 1) for use inside the NMR set-up. The specimen used in these sample holders were initially cut in cylindrical shapes of length 6 cm and diameter 2 cm. After drying in a furnace at 105 ± 5°C for 24 h these brick specimen were vacuum saturated in a 4 M NaCl solution. The longitudinal surfaces of the specimens were wrapped in Teflon tape to prevent evaporation while keeping their faces uncovered.

Fig. 1
figure 1

Schematic diagram of the sample holder used during diffusion and electromigration experiments (a) and during advection and advection-electromigration experiments (b)

Full size image

In order to study the transport of Na ions through fired-clay bricks three types of experiments were performed. First, the influence of concentration gradient, i.e. diffusion, on the transport of Na ions was studied by applying sponges, soaked with de-mineralized water, to the uncovered faces of the brick. Secondly, the transport of Na ions under the effect of a hydraulic gradient (i.e. advection) was observed by introducing a constant height difference in the water level of 2 cm across the sample. The combined effect of both the hydraulic and potential gradients i.e. advection–electromigration on the salt transport was also studied by exposing the specimen to both the potential and hydraulic gradients simultaneously. Thirdly, the effect of the intensity of applied electric field on the migration of Na ions was studied by using platinum mesh electrodes applied together with the wet sponges across the specimen.

In both diffusion and electromigration experiments the sponges were replaced after measuring each profile (i.e. after 30 min) to avoid any back diffusion of salt ions from the sponges to the brick and to suppress any variation in pH caused by the oxidation and reduction reactions at the anode and cathode respectively. Platinum electrodes were used to avoid the introduction of secondary corrosion products. During the electromigration experiments the current I (A) across the brick was continuously monitored and it was observed that it remained approximately constant during the entire experiment with in ~10%.

3.2 NMR set-up

NMR technique exploits the magnetic properties of nuclei possessing non-zero magnetic moments. When such nuclei are placed in an externally applied static magnetic field, their magnetic moments precess around the applied field. Depending on the strength of applied magnetic field B 0 (T), the resonance frequency or the so-called Larmor frequency f l (Hz) of these nuclei is given by [21]:

$$ f_{\text{l}} = \frac{{\gamma_{i} }}{2\pi }B_{0} $$
(15)

where the index i refers to the type of nucleus (H or Na), γ i (Hz T−1) is the gyromagnetic ratio (γH/2π = 42.58 MHz T−1; γNa/2π = 11.27 MHz T−1) which has a unique value for each nuclei.

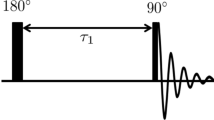
The NMR measurements reported in this article were performed using the so-called spin-echo technique [22]. The magnitude of NMR spin-echo signal is given by [21]:

$$ S \propto \alpha \rho \left[ {1 - \exp ( - {{t_{\text{r}} } \mathord{\left/ {\vphantom {{t_{\text{r}} } {t_{1} )}}} \right. \kern-\nulldelimiterspace} {t_{1} )}}} \right]\exp \left( {{{ - t_{\text{e}} } \mathord{\left/ {\vphantom {{ - t_{\text{e}} } {t_{2} }}} \right. \kern-\nulldelimiterspace} {t_{2} }}} \right) $$
(16)

where α is the relative sensitivity of particular nuclei in comparison with hydrogen (α = 0.093 for Na), ρ (mol l−1) the density of nuclei under investigation, t 1 (s) the spin-lattice (longitudinal) relaxation time, t r (s) the repetition time of the spin-echo experiment, t 2 (s) the spin–spin (transverse) relaxation time, and t e (s) the spin-echo time.

For the experiments described in this article a home-built NMR set-up was used. The schematic diagram of the NMR set-up is shown in Fig. 2.

Fig. 2
figure 2

A schematic diagram of the NMR set-up for measuring the moisture and Na during desalination experiments

Full size image

This NMR set up uses conventional electromagnets that produce magnetic field of 0.96 T. In order to measure quasi-simultaneously both the hydrogen and Na profiles during the desalination treatment, a specially designed RF circuit was incorporated [13]. A constant magnetic field gradient of 0.1 T m−1 was applied using Anderson coils, giving a one-dimensional spatial resolution of 1 and 4 mm for the hydrogen and Na respectively. First the moisture content in the small region of the sample near the centre of the RF coil is measured. Next the frequency is changed from H to Na and the Na content in that region is measured. After these two measurements the sample is moved in the horizontal direction and the moisture and Na contents are measured. This procedure is repeated until complete moisture and Na profile is measured.

In order to relate the variation in NMR signal intensities with the variation in Na concentration the calibration was performed on fired-clay brick before starting the experiments. A linear variation in Na signal intensity with the NaCl concentration, as is shown in Fig. 3, indicates that no adsorption of Na ions is taking place at the pore surfaces and as it is already reported by Pel et al. [23] the fired-clay bricks behave as inert materials. The variation in Na concentration profiles presented in the following section are calibrated by the Na signal intensity curve as shown in Fig. 3.

Fig. 3
figure 3

Variation in Na signal intensity as a function of NaCl concentration within the fired-clay brick

Full size image

4 Results and discussion

4.1 Diffusion experiment

The moisture and Na concentration profiles measured during the diffusion experiment are given in Fig. 4, in which the fired-clay brick is located between the vertical dashed lines. The lack of change in the moisture content of brick (Fig. 4a) indicates that drying did not take place during the entire experiment. The sharp peaks at both ends of the sample in Fig. 4a indicate the location of the sponges.

Fig. 4
figure 4

a Moisture and b Na concentration profiles in the fired-clay brick during the diffusion experiment including transformed profiles in the inset. The measurement time for each profile is 30 min

Full size image

In the absence of drying the symmetry of Na concentration profiles indicates that the brick specimen is homogenous and due to diffusion an equal amount of salt is removed from both sides of the brick. In order to verify that diffusion is the only transport process involved in salt transport the Boltzmann-Matano transformation λ = x/t 1/2 [24] was performed on both the left and right halves of the measured Na concentration profiles separately. The collapse of Na concentration profiles into a single master curve after the transformation confirmed that the transport of salt ions from both ends of the brick to the sponges is taking place due to diffusion. The Na concentration profiles from the left half of the brick after the Boltzmann–Matano transformation are shown in the inset of Fig. 4b. As it can be seen in the inset of Fig. 4b that the Na concentration profiles data after the transformation is fitted well by the solid curve obtained by using the error function:

$$ C = C_{0} {\text{erf}}\frac{\lambda }{{2\sqrt {D_{\text{eff}} } }} $$
(17)

with the following initial and boundary conditions:

$$ C = C_{0} ,\,{\text{at}}\,\lambda > 0,t = 0 $$
(18)
$$ C = 0,\,{\text{at}}\,\lambda = 0\,{\text{and}}\,C = C_{0} ,\,{\text{at}}\,\lambda \to \infty ,\,{\text{for}}\,{\text{all}}\,{\text{time}}\,t > 0 $$
(19)

where C 0 (mol l−1) is the initial Na concentration within the brick.

By using the above given initial and boundary conditions in Eq. 17 the diffusion coefficient of Na ions in the brick of the order of 0.80 × 10−9 m2 s−1 is obtained by curve fitting and is in good agreement with the reported values [15].

4.2 Advection experiment

The Na concentration profiles measured by maintaining a water level height difference of 2 cm across the salt contaminated brick specimen are shown in Fig. 5a. The profiles indicate a clear movement of Na ions from the left (higher water level) to the right (lower water level) side of the brick. The variation in position of the Na front (at the concentration level of 2 M) with time is linear and is shown in Fig. 5b. From the slope of the linear fit the Na front speed of 2.20 × 10−6 m s−1 was obtained.

Fig. 5
figure 5

a Na concentration profiles measured under the effect of advection by introducing a water level height difference of 2 cm. b The variation in position of Na front with time. The Na front position is taken approximately where the arrow is intersecting the Na profiles in a. The measurement time for each profile is 18 min

Full size image

By taking this value for the speed of the Na front as the volumetric flux, i.e. v h, and using it in Eq. 4 the intrinsic permeability of the fired-clay brick used in this experiment, of the order of 6 × 10−13 m2, was obtained and it is comparable to the permeability value of 10−12 m2 as reported by van der Heijden et al. [17].

4.3 Electromigration experiments

The influence of the applied electric field on the migration of Na ions was studied by applying potential gradients ranging from 0.75–2 V cm−1 across the specimen. Note that the actual potential gradient across the specimen is smaller than the applied gradient due to polarization of the electrodes. The measured Na concentration profiles under the applied potential gradients of 0.75 and 1.58 V cm−1 are shown in Fig. 6. It can be seen that the symmetry in the Na concentration profiles, which was observed during the diffusion experiment (Fig. 4b), is lost. A clear Na front profile is observed moving through the sample from the anode to the cathode, indicating that Na ions are moving towards the cathode. In the case of 1.58 V cm−1 the progression of Na front is much faster than at 0.75 V cm−1.

Fig. 6
figure 6

Na concentration profiles during application of potential gradients: a 0.75 V cm−1 and b 1.58 V cm−1. The arrows indicate the direction of the Na front as it moves from the anode deeper inside the brick towards the cathode. The measurement time for each profile is 30 min

Full size image

The position of Na front under applied field strengths (from 0.75–2 V cm−1) is shown in Fig. 7a. In all cases a linear increase in the position of Na front with time indicates a constant speed of the Na front. The Na front speed as a function of the applied potential gradients is given in Fig. 7b.

Fig. 7
figure 7

a Variation in the position of Na front as a function of time. b Average speed of Na front as a function of applied potential gradients

Full size image

From the slope of linear fit (Fig. 7b) the effective mobility (μ eff) of the Na ions obtained is of the order of 4.43 × 10−9 m2 s−1 V−1. However, this value is lower than the mobility derived from the diffusion experiment according to Eq. 9; which equals to 32 × 10−9 m2 s−1. This difference in mobilities might be attributed to the fact the actual potential gradients across the sample are smaller than the applied potential gradients due to polarization of electrodes.

4.4 Diffusion versus advection and electromigration

A comparison between each of the transport processes i.e. diffusion, advection and electromigration is made by taking into account their respective contribution in the reduction of Na concentration in fired-clay brick during the entire experiment. The variation in normalized Na concentration in the brick during diffusion, advection (Δh = 2 cm), and electromigration at different applied field strengths (from 0.75 to 2 V cm−1) is shown in Fig. 8. The normalization was performed by integrating the Na concentration of each measured profile over the entire brick and then dividing it with the integrated Na concentration profile of the same brick measured just before the start of experiment.

Fig. 8
figure 8

The variation in normalized Na concentration with time under the effect of diffusion, advection and electromigration at different applied field strengths. Above the dashed line Na transport is dominated by diffusion and below this line by electromigration and advection

Full size image

It can be seen that within the time scale of the experiments and the length of the specimen used, up to applied field strength of 1.20 V cm−1 diffusion is dominant over electromigration. At applied field strengths of 1.58 and 2 V cm−1 electromigration dominates the transport process. However, in these experiments advection was shown to be dominant over both diffusion and electromigration.

The results presented in Fig. 8 shows that, in comparison with diffusion and electromigration, salts can be efficiently removed by hydraulic advection from relatively high permeable materials like fired-clay bricks. However, the in situ removal of salts by hydraulic advection from building structures has severe limitations. Even in the case of very simple building structures made up of relatively high permeable materials i.e. fired-clay bricks it is difficult to expose the entire building to a hydraulic gradient.

In order to overcome these difficulties the injection-poultice technique has been developed for in situ use in the brickwork [3] where salt transport is accomplished by advection. In this method water is injected through deep holes bored into the joints of wall and the salt contaminated water is sucked back from the same side of the wall to the sponges either by capillary pressure due to drying or by pumping water using the pumps at the adjacent outer layer of the wall.

However, in the case of low permeable building materials e.g. mortar and concrete the salt transport by hydraulic advection is practically impossible due to extremely high hydraulic gradients requirement. In this type of materials electromigration is amongst the possible ways to accomplish salt extraction.

4.5 Scale analysis of transport processes

The results presented in the previous subsections show that all the transport processes i.e. diffusion, advection and electromigration can have significant effect on the transport of salt ions through fired-clay bricks. The dominance of any particular transport process can be determined by undertaking a scale analysis. The scale analysis regarding competition between diffusion–advection and diffusion-migration is made on the basis of Peclet number, Pe, defined as the ratio between the rates of transport by convection to the molecular diffusion [25]. In this study the Pe has been used to determine the competition between the processes that lead to directional mass transport (i.e. advection and electromigration) to the random mass transport i.e. diffusion. In the case of advection-electromigration, where both the processes lead to a directional mass transport, the scale analysis is made by introducing a new dimensionless number, ξ. In this analysis the characteristic length is the length of the specimen (i.e. 6 cm) that was used during the experiments.

4.5.1 Diffusion versus advection

In the case of diffusion–advection the competition between these transport processes is characterized by using the Peclet number, Pe, obtained by making dimensional analysis of Eq. 14:

$$ Pe = \frac{{\left| {v_{\text{h}} } \right|L}}{{D_{\text{eff}} }} $$
(20)

where v h denotes the velocity of solute i.e. the Na ions, D eff is the effective diffusion coefficient of the ions and L (m) is the length of the specimen used in the experiment. If Pe ≫ 1, then the transport of salt ions through the porous material is dominated by the hydraulic advection. For diffusion to be dominant over hydraulic advection the Peclet number must be less than one (i.e. Pe ≪ 1).

The competition between diffusion and advection can also be characterized by using Peclect number based on the time scales for both the transport processes and is given by:

$$ Pe = \frac{{{{L^{2} } \mathord{\left/ {\vphantom {{L^{2} } {D_{\text{eff}} }}} \right. \kern-\nulldelimiterspace} {D_{\text{eff}} }}}}{{{L \mathord{\left/ {\vphantom {L {v_{\text{h}} }}} \right. \kern-\nulldelimiterspace} {v_{\text{h}} }}}} = \frac{{\tau_{\text{diffusion}} }}{{\tau_{\text{advection}} }} $$
(21)

where τ diffusion (s) is the diffusion time and τ advection (s) is the time for hydraulic advection. By using D eff = 0.80 × 10−9 m2 s−1 as the diffusion coefficient as determined by diffusion experiment and v h = 2.20 × 10−6 m s−1 as the velocity of Na ions through the brick that was obtained during advection experiment, the Peclet number thus obtained is given by:

$$ Pe = \frac{{\tau_{\text{diffusion}} }}{{\tau_{\text{advection}} }} = 165 $$
(22)

This means that for a height difference of 2 cm the advection is dominant over diffusion and it is in agreement with the experimental results.

For diffusion to be in equilibrium with advection i.e. for Pe = 1, v h should be equal to 1.32 × 10−8 m s−1, which corresponds to height difference of less than 0.13 mm. In order for diffusion to dominate over advection, i.e. for Pe ≪ 1, the difference in water level across the brick should be much less than 0.1 mm.

At first such a significant effect on salt transport due to a relatively low pressure difference of 200 Pa caused by a 2 cm height difference across the fired-clay bricks seems to be unrealistic. However, depending on the permeability of materials even in the presence of extremely small pressure differences, as it is shown in the calculation for Peclet number, advection can dominate the diffusion transport. Poupeleer et al. [26] while performing diffusion experiments noted that the density differences in liquid in response to the variation in salt concentration in different compartments of a diffusion cell produced enough hydrostatic pressure differences across a ceramic brick to make advection a dominant transport mechanism.

4.5.2 Diffusion versus electromigration

From Eq. 14, the competition between diffusion and electromigration on salt transport can also be characterized by using a Peclet number:

$$ Pe = \left| {\frac{{\mu_{\text{eff}} V}}{{D_{\text{eff}} }}} \right| $$
(23)

In the case of using Eq. 23, if Pe ≫ 1, then electromigration will dominate, while for Pe ≪ 1 diffusion dominates. In terms of the time scales for both diffusion and electromigration the Peclect number is given by:

$$ Pe = \frac{{{{L^{2} } \mathord{\left/ {\vphantom {{L^{2} } {D_{\text{eff}} }}} \right. \kern-\nulldelimiterspace} {D_{\text{eff}} }}}}{{{{L^{2} } \mathord{\left/ {\vphantom {{L^{2} } {\mu_{\text{eff}} V}}} \right. \kern-\nulldelimiterspace} {\mu_{\text{eff}} V}}}} = \frac{{\tau_{\text{diffusion}} }}{{\tau_{\text{migration}} }} $$
(24)

In this case if Pe ≪ 1 then diffusion will dominate over electromigration and vice versa. The time τ diffusion taken by diffusion to desalinate a specimen of 6 cm length is of the order of 4.5 × 106 s. Conversely, the maximum time τ migration that corresponds to a 0.75 V cm−1 potential gradient is of the order of 2 × 105 s. Thus, according to Eq. 24 electromigration will be dominant during all the applied potential gradients (0.75–2 V cm−1). However, according to the experimental results (Fig. 8) electromigration dominates over diffusion after a potential gradient of 1.20 V cm−1 is applied.

4.5.3 Advection versus electromigration

In the case of advection–electromigration transport the dimensionless number ξ obtained from the dimensional analysis of Eq. 14 is:

$$ \xi = \left| {\frac{{\mu_{\text{eff}} V}}{{v_{\text{h}} L}}} \right| $$
(25)

The competition between advection and electromigration on salt transport in terms of ξ based on their time scales can be written as:

$$ \xi = \frac{{{L \mathord{\left/ {\vphantom {L {v_{\text{h}} }}} \right. \kern-\nulldelimiterspace} {v_{\text{h}} }}}}{{{{L^{2} } \mathord{\left/ {\vphantom {{L^{2} } {\mu_{\text{eff}} V}}} \right. \kern-\nulldelimiterspace} {\mu_{\text{eff}} V}}}} $$
(26)

By using the Na velocity v h = 2.20 × 10−6 m s−1 and μ eff = 4.43 × 10−9 m2 s−1 V−1 in Eq. 26, depending on the value of applied voltage, ξ lies between 0.1 and 0.4. These values suggest that both the advection and electromigration are comparable with each other. Therefore, it is possible to halt the transport of salt ions due to advection by applying a potential gradient in the opposite direction to that of advection.

This effect was experimentally verified when a potential gradient was applied in opposite direction to that of the movement of Na ions due to hydraulic gradient across the specimen and is shown in Fig. 9a. The Na concentration profiles shown by solid line represent the movement of Na ions due to hydraulic gradient by maintaining a height difference of 2.80 cm across the specimen. The effect of potential gradient of 2.85 V cm−1 applied in opposite to hydraulic gradient is represented by the dashed lines.

Fig. 9
figure 9

a Na concentration profiles represented by solid lines indicate the movement of Na ions through the brick under the effect of advection. The dashed lines show the Na profiles when both the hydraulic and field gradients were simultaneously applied in opposite direction to each other. b The variation in the position of Na front under the effect of only hydraulic gradient (i.e. advection) and under the simultaneous effect of both hydraulic and potential gradients applied in the opposite and in the same directions to each other. The measurement time for each profile is 18 min

Full size image

The corresponding Na front positions when the hydraulic and potential gradients are applied in opposite directions are represented by open triangles as shown in Fig. 9b. This figure also includes the front position of Na when hydraulic and potential gradients are applied in the same direction (open circles) and when only hydraulic gradient is applied (solid squares). In the case of only advection same results are again used that have already been presented in Fig. 5b. For both the advection-electromigration experiments the data represented by solid squares represent the position of Na front when no electric field was applied across the specimen. Although the removal of Cl ions is also important as they are responsible for the corrosion of e.g. reinforcements in concrete but the present study is limited to Na ions as in our NMR setup the sensitivity for Cl is too low.

5 Conclusions

It is possible to measure the transport of Na ions during electrokinetic desalination non-destructively using NMR. In the case of electromigration the salt (Na ions) removal rate is proportional to the applied electric field across the non-reactive porous materials. For electromigration to be dominant over diffusion a minimum level of electric field is necessary. Below this threshold electric field, diffusion is dominant over electromigration. Salt (Na ions) transport by advection is quite significant in the case of fired-clay bricks. The transport of Na ions can be enhanced if hydraulic and potential gradients are applied in the same direction, but if applied in opposing directions the rate of salt (Na ions) removal can be reduced or completely halted.

The results presented in this article and the conclusions drawn are based on relatively short term measurements (i.e. up to three and half hours). Moreover, the transport of salt ions only for one type of building materials i.e. fired-clay brick has been studied. In order to get better understanding about the role played by diffusion, advection and electromigration on the ionic transport the long term measurements on different types of porous building materials will be part of the future study.