Skip to main content
SpringerLink
Log in

Size effect on tensile softening relation

  • Original Article
  • Published:
Materials and Structures Aims and scope Submit manuscript

Abstract

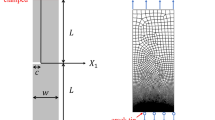
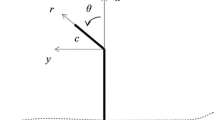
Tensile softening essential to the well-known fictitious crack model should be independent of specimen size and test methods. Commonly observed size effect (SE) on tensile softening relations measured from direct tensile specimens with smooth surface needs to be explained in order to determine the size independent tensile softening behaviour. In this paper, SE on tensile softening from direct tensile tests is elucidated by considering a boundary region where the key tensile softening mechanisms such as aggregate interlocking and frictional pull-out activities are limited in comparison with the inner region where those crack-bridging activities can be fully developed. SE on the tensile softening relation and the closely related specific fracture energy G f is inevitable if the boundary and inner regions are comparable. The same SE is gradually diminished with the increasing specimen size simply because the relative contribution from the boundary region is reduced in comparison with that from the increasing inner region. In principle, the size independent tensile softening relation and the size independent specific fracture energy G F in the inner region can be obtained by separating the influence of the boundary region from the test results.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

References

  1. Hillerborg A, Modeer M, Petersson PE (1976) Analysis of crack formation and crack growth in concrete by means of fracture mechanics and finite elements. Cem Concr Res 6:773–782

    Article  Google Scholar 

  2. Roelfstra PE, Wittmann FH (1986) Numerical method to link strain softening with failure of concrete. In: Wittmann FH (ed) Fracture toughness and fracture energy of concrete. Amsterdam, Elsevier, pp 163–175

  3. Hu XZ, Wittmann FH (1991) An analytical method to determine the bridging stress transferred within the fracture process zone: I, General Theory. Cem Concr Res 21(6):1118–1128

    Article  Google Scholar 

  4. Hu XZ, Wittmann FH (1992) An analytical method to determine the bridging stress transferred within the fracture process zone: II, Application to Mortar. Cem Concr Res 22:559–570

    Article  Google Scholar 

  5. van Vliet MRA, van Mier JGM (1998) Experimental investigation of size effect in concrete under uniaxial tension. In: Mihashi H, Rokugo K (eds) Fracture mechanics of concrete structures, Proc. FraMCoS-3, Japan, AEDIFICATIO Publishers, Freiburg, Germany, pp 1923–1936

  6. van Vliet MRA, van Mier JGM (1999) Effect of strain gradients on the size effect of concrete in uniaxial tension. Int J Fract 95:195–219

    Article  Google Scholar 

  7. Ostergaard L, Olesen JF (2004) Comparative study of fracture mechanical test methods for concrete. In: Li VC, William KJ, Leung CKY, Billington SL (eds) Fracture mechanics of concrete structures, FraMCos-5, 12–16 April 2004, Vail, Colorado, USA, Ia-FraMCos, 2004, vol 1, pp 455–462

  8. Villmann B, Villmann T, Slowik V (2004) Determination of softening curves by backward analyses of experiments and optimisation using an evolutionary algorithm. In: Li VC, William KJ, Leung CKY, Billington SL (eds) Fracture mechanics of concrete structures, FraMCos-5, 12–16 April 2004, Vail, Colorado, USA, Ia-FraMCos, 2004, vol 1, pp 439–445

  9. Akita H, Alterman D, Koide H (2008) Size effect of concrete in uniaxial tension. Adv Mater Res 41–42:227–232

    Article  Google Scholar 

  10. Hu XZ (1989) Fracture process zone and strain softening in cementitious materials. Building materials reports No. 1. Aedificatio Publishers, IRB Verlag, Freiburg i. Br., Germany (2nd edn. 1994)

  11. Hu XZ, Wittmann FH (1992) Fracture energy and fracture process zone. Mater Struct 25:319–326

    Article  Google Scholar 

  12. Abdalla HM, Karihaloo BL (2004) A method for constructing the bilinear tension softening diagram of concrete corresponding to its true fracture energy. Mag Concr Res 56(10):597–604

    Google Scholar 

  13. van Mier JGM (2004) Reality behind fictitious cracks. In: Li VC et al. (eds) Fracture mechanics of concrete structures, FraMCos-5, 12–16 April 2004, Vail, Colorado, USA, Ia-FraMCos, vol 1, pp 11–30

  14. Duan K, Hu, Hu XZ, Wittmann FH (2003) Thickness effect on fracture energy of cementitious materials. Cem Concr Res 33(4):499–507

  15. Hu XZ, Duan K (2004) Influence of fracture process zone height on fracture energy of concrete. Cem Concr Res 34:1321–1330

    Article  Google Scholar 

  16. Duan K, Hu XZ, Wittmann FH (2007) Size effect on specific fracture energy of concrete. Eng Fract Mech 74:87–96

    Article  Google Scholar 

  17. Bazant ZP (1984) Size effect on blunt fracture: concrete, rock, metal. J Eng Mech (ASCE) 110(4):518–535

    Article  Google Scholar 

  18. Hu XZ (1998) Size effects in toughness induced by crack close to free edge. In: Mihashi H, Rokugo K (eds) Fracture mechanics of concrete structures, Proc. FraMCoS-3, Japan, Aedificatio Publishers, Freiburg, Germany, pp 2011–2020

  19. Hu XZ (2002) An asymptotic approach to size effect on fracture toughness and fracture energy of composites. Eng Fract Mech 69:555–564

    Article  Google Scholar 

  20. Karihaloo BL, Abdalla HM, Xiao QZ (2003) Size effect in concrete beams. Eng Fract Mech 70:979–993

    Article  Google Scholar 

  21. Bazant ZP, Yu Q (2004) Size effect in fracture of concrete specimens and structures: new problems and progress. In: Li VC et al. (eds) Fracture mechanics of concrete structures, Ia-FraMcCos, Proceedings of the 5th international conference on fracture mechanics of concrete and concrete structures, Vail Colorado, USA, 12–16 April, 2004, pp 153–162

  22. Duan K, Hu XZ (2004) Asymptotic analysis of boundary-effect on strength of concrete. In: Li VC et al. (eds) Fracture mechanics of concrete structures, FraMCos-5, 12–16 April 2004, Vail, Colorado, USA, Ia-FraMCos, vol 1, pp 197–204

  23. Duan K, Hu XZ (2005) Application of boundary effect model to quasi-brittle fracture of concrete and rock. J Adv Concr Technol 3(3):413–422

    Article  Google Scholar 

  24. Duan K, Hu XZ, Wittmann F (2006) Scaling of quasi-brittle fracture: boundary and size effect. Mech Mater 38:128–141

    Article  Google Scholar 

  25. Hu XZ, Duan K (2007) Size effect: influence of proximity of fracture process zone to specimen boundary. Eng Fract Mech 74:1093–1100

    Article  Google Scholar 

  26. Hu XZ, Duan K (2008) Size effect and quasi-brittle fracture: the role of FPZ. Int J Fract 153:3–14

    Article  Google Scholar 

  27. Bazant ZP, Yu Q (2009) Universal size effect law and effect of crack depth on quasi-brittle structure strength. J Eng Mech (ASCE) 135(2):78–84

    Article  Google Scholar 

  28. Hu XZ, Duan K (2010) Mechanism behind the size effect phenomenon. J Eng Mech (ASCE) 136:60–68

    Google Scholar 

  29. Weibull W (1939) The phenomenon of rupture in solids. Proc., Royal Swedish Institute of Engineering Research, vol 153, Ingenioersvetenskaps Akad. Handl., Stockholm, pp 1–55

  30. Weibull W (1951) A statistical distribution function of wide applicability. J Appl Mech 18(3):293–297

    MATH  Google Scholar 

  31. Hu XZ, Cotterell B, Mai YW (1985) A statistical theory of fracture in a two-phase brittle material. Proc R Soc Lond A401:251–265

    MathSciNet  Google Scholar 

  32. Hu XZ, Cotterell B, Mai YW (1988) The statistics of brittle fracture of small specimens. Philos Mag Lett 57:69–73

    Article  Google Scholar 

  33. Hu XZ, Mai YW, Cotterell B (1988) A statistical theory of time-dependent fracture for brittle materials. Philos Mag 58:299–324

    Google Scholar 

  34. Hu XZ, Mai YW, Cotterell B (1992) Tensile strength of short-fibre-reinforced brittle materials with pre-existing defects. Philos Mag A 64:1265–1279

    Article  Google Scholar 

  35. Trunk B, Wittmann FH (1998) Influence of element size on fracture mechanics parameters of concrete. Dam Eng 9(1):3–24

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Mechanical Engineering, University of Western Australia, Perth, WA, 6009, Australia

    Xiaozhi Hu

Authors
  1. Xiaozhi Hu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Xiaozhi Hu.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Hu, X. Size effect on tensile softening relation. Mater Struct 44, 129–138 (2011). https://doi.org/10.1617/s11527-010-9614-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1617/s11527-010-9614-8

Keywords

Search

Navigation