Abstract
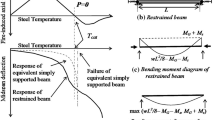
At room temperature, and at service load levels, creep has little effect on the performance of steel structures. However, under fire conditions, creep becomes a dominant factor and influences fire resistance of steel members. Under fire conditions, significant forces develop in restrained steel beams and these forces induce high stresses in the steel section. The extent of creep deformations is affected by magnitude and rate of development of stress and temperature in steel. In this paper, the effect of high temperature creep on fire response of restrained beams is investigated. Current high temperature creep models are compared. Finite element model created in ANSYS was validated by comparing the predictions with fire test data. The validated model was applied to investigate the effect of load level, heating rate, fire scenario and fire induced axial restraint on the extent of creep deformations. Results from the parametric study indicate that the influence of high temperature creep increases with the increase in axial restraint, heating rate, and load level. Generally, neglecting high-temperature creep effect stiffens the structural response and leads to reduced deflections but larger restraint forces. Therefore, neglecting high temperature creep in fire resistance analysis of steel structures can lead to unconservative predictions.












Similar content being viewed by others
Abbreviations
- B, n :
-
Constants in Dorn’s creep formulation, that depend on the type of steel
- ΔH :
-
Activation energy of creep (Btu/lb mole)
- c 1, …,c 7 :
-
Experimental coefficients of ANSYS creep model (see text for units)
- θ :
-
Dorn’s temperature-compensated time (h)
- Q :
-
ΔH/R = Constant of the compensated time formula in Dorn’s model (Rankine)
- R :
-
Gas universal constant (Btu/lb mole R)
- SΦ(σ s ):
-
Temperature–stress-dependent function in Dorn’s formulation of creep strain rate
- σ s :
-
Stress in steel (MPa)
- t :
-
time (min)
- T s :
-
Steel temperature (°C)
- T R :
-
Steel temperature (Rankine)
- Z:
-
Zener-Hollomon experimental parameter (h−1)
References
Harmathy T (1967) A comprehensive creep model. J Basic Eng 89(D-3):496–502
Williams-Leir G (1983) Creep of structural steel in fire: analytical expressions. Fire and Materials 7(2):73–80
Anderberg Y (1988) Modelling steel behaviour. Fire Safety J 13(1):17–26
Dorn JE (1954) Some fundamental experiments on high temperature creep. J Mech Phys Solids 3:85
Huang ZF, Tan KH (2003) Analytical fire resistance of axially restrained steel columns. J Struct Eng 129(11):1531–1537
Shames IH, Cozzarelli FA (1992) Elastic and inelastic stress analysis. Prentice Hall, Englewood Cliffs, NJ, pp 221–228
Tan KH, Ting SK, Huang ZF (2002) Visco-elasto-plastic analysis of steel frames in fire. J Struct Eng 128(1):105–114
Zienkiewicz OC, Cormeau IC (1974) Visco-plasticity—plasticity and creep in elastic solids—a unified numerical solution approach. Int J Numer Method Eng 8:821–845
KK N (1989) Fire-resistant steel for building structural use. Nippon Steel Corporation, Tokyo
Kirby BR, Preston RR (1988) High temperature properties of hot-rolled, structural steels for use in fire engineering design studies. Fire Safety J 13:27–37
Harmathy T, Stanzak W (1970) Elevated-temperature tensile and creep properties of some structural and prestressing steels. American Society for Testing and Material, special publication 186–208
Li G-Q, Guo S-X (2007) Experiment on restrained steel beams subjected to heating and cooling. J Construct Steel Res (in press)
EN1993-1-2 (2005) The European standard; Part 1–2: general rules—structural fire design. European Committee for Standardization, Brussels
ASCE (1992) Structural fire protection. Manual no. 78, American Society of Civil Engineers, Structural Division, ASCE committee on fire protection, New York
Poh KW (2001) Stress-strain-temperature relationship for structural steel. J Mater Civil Eng 13(5):371–379
Ding J, Li G-Q, Sakumoto Y (2004) Parametric studies on fire resistance of fire-resistant steel members. J Construct Steel Res 60:1007–1027
ASTM (2001) Standard methods of fire test of building construction and materials: test method E119-01. American Society for Testing and Materials, West Conshohocken, PA
EN1991-1-5 (2003) The European standard; Part 1–5: general actions—thermal actions. European Committee for Standardization, Brussels
Acknowledgments
The research presented in this paper is supported by the National Science Foundation (Grant No. 0652292) and Department of Commerce/National Institute of Standards and Technology (Grant No. 60NANB7D6120). Any opinions, findings, and conclusions or recommendations expressed in this paper are those of the authors and do not necessarily reflect the views of the sponsors.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Kodur, V.K.R., Dwaikat, M.M.S. Effect of high temperature creep on the fire response of restrained steel beams. Mater Struct 43, 1327–1341 (2010). https://doi.org/10.1617/s11527-010-9583-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1617/s11527-010-9583-y