Skip to main content
SpringerLink
Log in

Comparison between solid and hollow reinforced concrete beams

  • Original Article
  • Published:
Materials and Structures Aims and scope Submit manuscript

Abstract

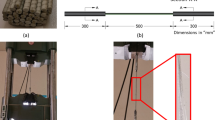
Comparison between test results of seven hollow and seven solid reinforced concrete beams is presented. All of the fourteen beams were designed as hollow sections to resist combined load of bending, torsion and shear. Every pair (one hollow and one solid) was designed for the same load combinations and received similar reinforcement. The beams were 300 × 300 mm cross-section and 3,800 mm length. The internal hollow core for the hollow beams was 200 × 200 mm creating a peripheral wall thickness of 50 mm. The main variables studied were the ratio of bending to torsion which was varied between 0.19 and 2.62 and the ratio in the web of shear stress due to torsion to shear stress due to shear force which was varied between 0.59 and 6.84. It was found that the concrete core participates in the beams’ behaviour and strength and cannot be ignored when combined load of bending, shear and torsion are present. Its participation depends partly on the ratio of the torsion to bending moment and the ratio of shear stress due to torsion to the shear stress due to shear force. All solid beams cracked and failed at higher loads than their counterpart hollow beams. The smaller the ratio of torsion to bending the larger the differences in failure loads between the hollow and solid beams. The longitudinal steel yielded while the transverse steel experienced lower strain values.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12

Similar content being viewed by others

Abbreviations

ε/εy :

Ratio of applied strain at each increment to yield strain

(ε/εy)Lng:

Maximum strain ratio measured in the longitudinal steel

(ε/εy)Strp:

Maximum strain ratio measured in the stirrups

Dif. F.L:

Percentage of the difference in failure load between the solid and hollow beams

f′c :

Concrete cylinder compressive strength

f cu :

Concrete cube compressive strength

f′t :

Concrete cylinder tensile split test

f y :

Yield stress of the longitudinal steel

f yv :

Yield stress of the transverse steel

L.F:

Load factor (percentage of applied load to design load) = (T i/T d + M i/M d)/2 at any load increment i

L e/L d :

Failure load ratio = (T e/T d + M e/M d)/2 for the last (failure) load increment

LFCR :

Load factor when first crack was noticed

M d, T d, V d :

Design bending moment, torsion and shear force respectively

M e, T e, V e :

Experimentally measured bending moment, torsion and shear force at failure respectively

T i, M i, V i :

Experimentally measured torsion, bending moment and shear force at load increment i

θ o :

Average angle of inclination of cracks near failure load

Δ:

Maximum vertical displacement at mid-span

σy :

Applied normal stress in the y direction

τshr :

Applied shear stress due to shear force

τtor :

Applied shear stress due to torsion

τxy+:

Net applied shear stress due to torsion and shear where stresses are added, (=τshr + τtor)

τ xy−:

Net applied shear stress due to torsion and shear where stresses are subtracted, (=τshr−τtor)

N x :

Applied in-plane force per unit length in the x direction on a element with thickness t, (=σxser t)

N y :

Applied in-plane force per unit length in the y direction on a element with thickness t, (=σy t)

N xy :

Applied in-plane shear force per unit length on a element with thickness t, (=τ xy t)

N sx :

Steel resisting force in x direction

N sy :

Steel resisting force in y direction

σ1 :

Concrete principle stress in direction 1

σ2 :

Concrete principle stress in direction 2

N 1 :

Concrete resisting force in the principle direction 1, (=σ 1 t)

N 2 :

Concrete resisting force in the principle direction 2, (=σ 2 t)

A o :

Area of concrete enclosed by the centre line of the shear flow

A c :

Concrete gross cross-sectional area

I :

Moment of inertia of the cross-section

References

  1. Hsu TTC (1968) Torsion of structural concrete-behaviour of reinforced concrete rectangular members. SP-18, American Concrete Institute, Detroit, Michigan, pp 261–306

  2. Mitchell, D, Collins MP (1974) Behaviour of structural concrete beams in pure torsion, publication No. 74–06. Department of Civil Engineering, University of Toronto, Toronto, Ontario, Canada

  3. Ojha Surendra K (1974) Deformation of reinforced concrete rectangular beams under combined torsion, bending and shea. ACI J 71–26:383–391

    Google Scholar 

  4. Thurlimann B (1979) Torsional strength of reinforced and prestressed concrete beams-CEB approach. Institut fur Baustatik und konstruktion, ETH. Zurich, (92):117–143

  5. Collins MP, Mitchell D (1991) Pre-stressed concrete structures. Prentice Hall Inc., Englewood Cliffs, NJ

  6. Rahal KN, Collins MP (1995) Analysis of sections subjected to combined shear and torsion—a theoretical model. ACI Struct J 92(4):459–469

    Google Scholar 

  7. Rahal KN (2000) Torsional strength of reinforced concrete beams. Canadian J Civil Eng 27:445–453

    Article  Google Scholar 

  8. MacGregor JG, Ghoneim MG (1995) Design for torsion. ACI Struct J S92–S20:211–218

    Google Scholar 

  9. Fouad E, Ghoneim M, Issa M, Shaheen H (2000) Combined shear and torsion In normal and high-strength concrete beams (1): Experimental Study. J Eng Appl Sci 47(6):1059–1078

    Google Scholar 

  10. Bhatt P, Ebireri JO (1989) Direct design of beams for combined bending and torsion, Stavebnicky Casopis, Building Journal (Bratislava), v 37, n 4 Apr., pp 249–263, in English, ISSN: 0039-078X, Coden: STVCA2

  11. Nielsen TB (1985) Optimization of reinforcement in shells, folded plates, walls and slabs. ACI J 82–26:304–309

    Google Scholar 

  12. Nielsen MP (1978) Some examples of lower-bound design of reinforcement in plane stress problems. IABSE colloquium, Copenhagen, Session V. Plasticity in Reinforced Concrete, Final report 29:317–324 Aug

    Google Scholar 

  13. Nielsen MP (1974) Optimum design of reinforced concrete shells and slabs. Structural research laboratory, Technical University of Denmark, Report NR.R44, pp 190–200

  14. Alnuaimi AS, Bhatt P (2004) Direct design of hollow reinforced concrete beams, part I: design procedure. Struct Concrete J 5(4):139–146

    Article  Google Scholar 

  15. Alnuaimi AS, Bhatt P (2004) Direct design of hollow reinforced concrete beams, part II: experimental investigation. Struct Concrete J 5(4):147–160

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Civil and Architectural, Engineering College of engineering, Sultan Qaboos University, P.O. Box 33, Al Khodh 123, Muscat, Sultanate of Oman

    Ali Said Alnuaimi, Khalifa S. Al-Jabri & Abdelwahid Hago

Authors
  1. Ali Said Alnuaimi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Khalifa S. Al-Jabri
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Abdelwahid Hago
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Ali Said Alnuaimi.

Appendix A

Appendix A

1.1 Design example

Use the Direct Design Method to design a reinforced concrete hollow beam for M d = 50.9kN.m, V d = 61.08 kN and T d = 13 kN.m. The cross-section is 300 mm with 200 × 200 mm hollow core. The characteristic material strengths are f y = 490N/mm2 for longitudinal steel, f yv = 472N/mm2 for stirrups and f cu = 38N/mm2 for concrete.

1.2 Solution

The section is divided into six regions (levels) a–f as shown in Fig. A1a.

Fig. A1
figure A1

Cross section of the hollow beam

Full size image
$$ I{\hbox{ = }}\left( {\frac{{300^3 \times 200}} {{12}} - \frac{{200^3 \times 200}} {{12}}} \right){\hbox{ = 5}}{\hbox{.42}} \times {\hbox{10}}^{\hbox{8}}\, {\hbox{mm}}^{\hbox{4}} $$

A o = 250( × 250 = 6.25 × 104 mm2 (area enclosed by the dotted line of Fig. A1b)

1.3 Normal stresses due to bending

For elastic stress distribution, equation A1 can be used.

$$ \sigma _x = \pm \frac{{My}} {I} $$

The results are presented in column 2 of Table A1.

Table A1 Stress calculation at each region
Full size table

No out-of-plane bending is considered, σy = 0 at all regions (column 3 of Table A1).

1.4 Shear stresses due to shear force

Equation A2 is used for the calculation of shear stresses due to shear force.

$$ \tau _{shr} = \frac{{V\int {yd} }} {{It}} $$
(A2)

The result is shown in column 4 of Table A1.

1.5 Shear stresses due to torsion

Shear flow is assumed to circulate in the outer 50 mm thick skin.

Equation A3 is used for the calculation of shear stress due to torsion. The result is shown in column 5 of Table A1.

$$ \tau _t = \frac{T} {{2bA_o }} $$
(A3)

Resulting shear stresses at each region are given in the last two columns of Table A1. \(\tau _{xy} \) -represents the net shear stress where the shear stress due to torsion and the shear stress due to shear force are subtractive while \(\tau _{xy}+ \) represents the net shear stress where the shear stresses are additive. For practical reasons, \(\tau _{xy}\)+ was considered in the calculation of steel areas. Net design normal and shear stresses at each level can be schematically represented as shown in Fig. A2.

Fig. A2
figure A2

schematic representation of element normal and shear stresses at each region

Full size image

1.6 Calculation of forces per unit length and selection of design equations

The values of the ratios of \(\frac{{\sigma _x }} {{\left| {\tau _{xy} } \right|}}\) and \({\hbox{ }}\frac{{\sigma _{\hbox{y}} }} {{\left| {\tau _{xy} } \right|}}{\hbox{ }}\) (columns 2, 3 and 7 of Table A1) were used to select design equations from Fig. A3 (for equation derivations and boundary curves, see Alnuaimi and Bhatt 14–15). Accordingly, the required reinforcement is calculated using Eqs. A4 and A5. The results are shown in Table A2.

Fig. A3
figure A3

Boundary graph for Nielsen’s design equations

Full size image
Table A2 Calculation of forces and reinforcement in the longitudinal and transverse directions
Full size table
$$ A_s = \frac{{N_x^s }} {{f_y }}w $$
(A4)
$$ A_{sv} = \frac{{N_y^s }} {{f_{yv} }}1000 $$
(A5)

NB. It should be noted that in this example there was no need for longitudinal reinforcement in the top flange. However, for the purpose of anchoring the stirrups, two bars of 8 mm diameter have to be provided.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Alnuaimi, A.S., Al-Jabri, K.S. & Hago, A. Comparison between solid and hollow reinforced concrete beams. Mater Struct 41, 269–286 (2008). https://doi.org/10.1617/s11527-007-9237-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1617/s11527-007-9237-x

Keywords

Search

Navigation