Abstract
A numerical nanoindentation model was developed using the Material Point Method (MPM), which was chosen because it can handle both large deformations and dynamic contact under the indenter. Because of the importance of contact, prior MPM contact methods were enhanced to improve their accuracy for contact detection. Axisymmetric and full 3D simulations investigated the effects of hardening, strain-rate dependent yield properties, and local structure under the indenter. Convergence of load-displacement curves required small cells under the indenter. To reduce computation time, we used an effective nonregular grid, called a tartan grid and describe its implementation. Tartan grids reduced simulation times by an order of magnitude. A series of simulated load-displacement curves were analyzed as “virtual experiments” by standard Oliver-Pharr methods to extract effective modulus and hardness of the indented material. We found that standard analysis methods give results that are affected by hardening parameters and strain-rate dependence of plasticity. Because these parameters are not known during experiments, extracted properties will always have limited accuracy. We describe an approach for extracting more properties and more accurate properties by combining MPM simulations with inverse methods to fit simulation results to entire load-displacement curves.








Similar content being viewed by others
References
W.C. Oliver and G.M. Pharr: An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments. J. Mater. Res. 7, 1564–1583 (1992).
B. Poon, D. Rittel, and G. Ravichandran: An analysis of nanoindentation in elasto-plastic solids. Int. J. Solid Struct. 45, 6399–6415 (2008).
B. Poon, D. Rittel, and G. Ravichandran: An analysis of nanoindentation in linearly elastic solids. Int. J. Solid Struct. 45, 6018–6033 (2008).
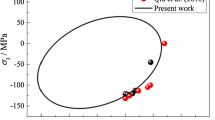
X. Chen, I. Ashcroft, C. Tuck, Y. He, R. Hague, and R. Wildman: An investigation into the depth and time dependent behavior of UV cured 3D ink jet printed objects. J. Mater. Res. 32, 1407–1420 (2017).
T. Nardi, C. Hammerquist, J.A. Nairn, A. Karimi, J-A.E. Månson, and Y. Leterrier: Nanoindentation of functionally graded polymer nanocomposites: Assessment of the strengthening parameters through experiments and modeling. Front. Mater. 2, 57 (2015).
J. Ma, Y. Liu, H. Lu, and R. Komanduri: Multiscale simulation of nanoindentation using the generalized interpolation material point (GIMP) method, dislocation dynamics (DD) and molecular dynamics (MD). Comput. Model. Eng. Sci. 16, 41–55 (2006).
S. Bardenhagen, J.E. Guilkey, K. Roessig, J. Brackbill, W. Witzel, and J. Foster: An improved contact algorithm for the material point method and application to stress propagation in granular material. Comput. Model. Eng. Sci. 2, 509–522 (2001).
J.A. Nairn: Modeling imperfect interfaces in the material point method using multimaterial methods. Comput. Model. Eng. Sci. 1, 1–15 (2013).
J.A. Nairn, S.G. Bardenhagen, and G.S. Smith: Generalized contact and improved frictional heating in the material point method. Comput. Part. Mech. (2017). doi: https://doi.org/10.1007/s40571-017-0168-1.
S.G. Bardenhagen and E.M. Kober: The generalized interpolation material point method. Comput. Model. Eng. Sci. 5, 477–496 (2004).
D. Sulsky, Z. Chen, and H.L. Schreyer: A particle method for history-dependent materials. Comput. Meth. Appl. Mech. Eng. 118, 179–186 (1994).
X. Zhang, Z. Chen, and Y. Liu: The Material Point Method: A Continuum-Based Particle Method for Extreme Loading Cases (Academic Press, Oxford, U.K., 2016).
J.A. Nairn: Numerical simulations of transverse compression and densification in wood. Wood Fiber Sci. 38, 576–591 (2007).
P. Perré, G. Almeida, M. Ayouz, and X. Frank: New modelling approaches to predict wood properties from its cellular structure: Image-based representation and meshless methods. Ann. For. Sci. 73, 147–162 (2016).
J.A. Nairn: Material point method simulations of transverse fracture in wood with realistic morphologies. Holzforschung 61, 375–381 (2007).
J.E. Guilkey, J.B. Hoying, and J.A. Weiss: Computational modeling of multicellular constructs with the material point method. J. Biomech. 39, 2074–2086 (2006).
S. Ganpule, N.P. Daphalapurkar, K.T. Ramesh, A.K. Knutsen, D.L. Pham, P.V. Bayly, and J.L. Prince: A three-dimensional computational human head model that captures live human brain dynamics. J. Neurotrauma 34, 2154–2166 (2017).
N.P. Daphalapurkar, J.C. Hanan, N.B. Phelps, H. Bale, and H. Lu: Tomography and simulation of microstructure evolution of a closed-cell polymer foam in compression. Mech. Adv. Mater. Struct. 15, 594–611 (2008).
A. Stomakhin, C. Schroeder, L. Chai, J. Teran, and A. Selle: A material point method for snow simulation. ACM Trans. Graph. 32, 1–102 (2013).
S. Bardenhagen, J. Brackbill, and D. Sulsky: The material-point method for granular materials. Comput. Meth. Appl. Mech. Eng. 187, 529–541 (2000).
Y. Wang, H. Beom, M. Sun, and S. Lin: Numerical simulation of explosive welding using the material point method. Int. J. Impact Eng. 38, 51–60 (2011).
S. Ma and X. Zhang: Material point method for impact and explosion problems. In Proceedings of International Symposium on Computational Mechanics, Z. Yao, M. Yuan, eds. (Springer, Beijing, China, 2007); pp. 156–166.
J.A. Nairn: Material point method calculations with explicit cracks. Comput. Model. Eng. Sci. 4, 649–664 (2003).
S.G. Bardenhagen, J.A. Nairn, and H. Lu: Simulation of dynamic fracture with the material point method using a mixed J-integral and cohesive law approach. Int. J. Fract. 170, 49–66 (2011).
R. Ambati, X. Pan, H. Yuan, and X. Zhang: Application of material point methods for cutting process simulations. Comput. Mater. Sci. 57, 102–110 (2012).
J.A. Nairn: Numerical simulation of orthogonal cutting using the material point method. Eng. Fract. Mech. 149, 262–275 (2015).
P.G. Hu, L. Xue, S. Mao, R. Kamakoti, H. Zhao, N. Dittakavi, Z. Wang, Q. Li, K. Ni, and M. Brenner: Material point method applied to fluid-structure interaction (FSI)/aeroelasticity problems. In 48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition (Orlando, Florida, 2010); pp. 4–7.
J.A. Nairn: Material point method (NairnMPM) and finite element analysis (NairnFEA) open-source software (2017). Available at: http://osupdocs.forestry.oregonstate.edu/index.php/Main_Page (accessed March 16, 2018).
J.A. Nairn and J.E. Guilkey: Axisymmetric form of the generalized interpolation material point method. Int. J. Numer. Meth. Eng. 101, 127–147 (2015).
W. Oliver and G. Pharr: Measurement of hardness and elastic modulus by instrumented indentation: Advances in understanding and refinements to methodology. J. Mater. Res. 19, 3–20 (2004).
A. Clausner and F. Richter: Usage of the concept of the effectively shaped indenter for the determination of yield stress from berkovich nano-indentation experiments. Eur. J. Mech. Solid. 53, 294–302 (2015).
A. Bower: Applied Mechanics of Solids (CRC Press, Boca Raton, Florida, 2009). ISBN: 9781439802489.
T. Chudoba and F. Richter: Investigation of creep behaviour under load during indentation experiments and its influence on hardness and modulus results. Surf. Coat. Technol. 148, 191–198 (2001).
J.E. Jakes, C.R. Frihart, J.F. Beecher, R.J. Moon, and D. Stone: Experimental method to account for structural compliance in nanoindentation measurements. J. Mater. Res. 23, 1113–1127 (2008).
M.R. VanLandingham, J.S. Villarrubia, W.F. Guthrie, and G.F. Meyers: Nanoindentation of polymers: An overview. In Macromolecular Symposia, Vol. 167 (Wiley-Blackwell, Hoboken, New Jersey, 2001); pp. 15–44.
G.R. Johnson and W.H. Cook: A constitutive model and data for metals subjected to large strains, high strain rates and high. In Proceedings of the 7th International Symposium on Ballistics (The Hague, The Netherlands, 1983); pp. 541–547.
V. Lemiale, A. Hurmane, and J.A. Nairn: Material point method simulation of equal channel angular pressing involving large plastic strain and contact through sharp corners. Comput. Model. Eng. Sci. 70, 41–66 (2010).
A. Sadeghirad, R.M. Brannon, and J. Burghardt: A convected particle domain interpolation technique to extend applicability of the material point method for problems involving massive deformations. Int. J. Numer. Meth. Eng. 86, 1435–1456 (2011).
C.C. Hammerquist and J.A. Nairn: A new method for material point method particle updates that reduces noise and enhances stability. Comput. Meth. Appl. Mech. Eng. 318, 724–738 (2017).
C.M. Mast, P. Arduino, G.R. Miller, and P. Mackenzie-Helnwein: Avalanche and landslide simulation using the material point method: Flow dynamics and force interaction with structures. Comput. Geosci. 18, 817–830 (2014).
S. Mao, Q. Chen, D. Li, and Z. Feng: Modeling of free surface flows using improved material point method and dynamic adaptive mesh refinement. J. Eng. Mech. 142, 04015069 (2016).
J. Ma: Multiscale simulation using the generalized interpolation material point method, discrete dislocations and molecular dynamics. Ph.D. thesis, Oklahoma State University, Stillwater, Oklahoma, 2006.
P-L. Larsson, A. Giannakopoulos, E. Söderlund, D. Rowcliffe, and R. Vestergaard: Analysis of berkovich indentation. Int. J. Solid Struct. 33, 221–248 (1996).
R Core Team: R: A Language and Environment for Statistical Computing (R Foundation for Statistical Computing, Vienna, Austria, 2016). Available at: https://www.R-project.org/.
M. Troyon and S. Lafaye: About the importance of introducing a correction factor in the sneddon relationship for nanoindentation measurements. Philos. Mag. 86, 5299–5307 (2006).
J. Graf: PID Control Fundamentals (Createspace Independent Publishing Platform, 2016). ISBN: 9781535358668.
G.M. Pharr and A. Bolshakov: Understanding nanoindentation unloading curves. J. Mater. Res. 17, 2660–2671 (2002).
G. Fu and L. Cao: On the effective indenter shape used in the analysis of nanoindentation unloading curves. J. Mater. Sci. 40, 2683–2684 (2005).
X. Chen, N. Ogasawara, M. Zhao, and N. Chiba: On the uniqueness of measuring elastoplastic properties from indentation: The indistinguishable mystical materials. J. Mech. Phys. Solid. 55, 1618–1660 (2007).
ACKNOWLEDGMENT
The work was funded by the National Institute of Food and Agriculture (NIFA) of the United States Department of Agriculture (USDA), Grant No. 2013-34638-21483.
Author information
Authors and Affiliations
Corresponding author
Supplementary Material
Rights and permissions
About this article
Cite this article
Hammerquist, C.C., Nairn, J.A. Modeling nanoindentation using the Material Point Method. Journal of Materials Research 33, 1369–1381 (2018). https://doi.org/10.1557/jmr.2018.75
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1557/jmr.2018.75