Skip to main content
SpringerLink
Log in

A new approach of the Oliver and Pharr model to fit the unloading curve from instrumented indentation testing

  • Article
  • Published:
Journal of Materials Research Aims and scope Submit manuscript

Abstract

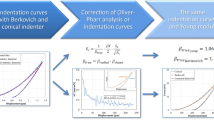
The unloading part of a load–displacement curve from instrumented indentation tests is usually approximated by a power law (Oliver and Pharr model), where the load is the dependent variable. This approach generally fits well the data. Nevertheless, the convergence is occasionally quite questionable. In this regard, we propose a different approach for the Oliver and Pharr model, called the inverted approach, since it assigns the displacement as the dependent variable. Both models were used to fit the unloading curves from nanoindentation tests on fused silica and aluminum, applying a general least squares procedure. Generally, the inverted methodology leads to similar results for the fitting parameters and the elastic modulus (E) when convergence is achieved. Nevertheless, this approach facilitates the convergence, because it is a better conditioned problem. Additionally, by Monte Carlo simulations we found that robustness is improved using the inverted approach, since the estimation of E is more accurate, especially for aluminum.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

FIG. 1
FIG. 2
FIG. 3
FIG. 4
FIG. 5
FIG. 6
FIG. 7

Similar content being viewed by others

References

  1. M.R. VanLandingham: Review of instrumented indentation. J. Res. Natl. Inst. Stand. Technol. 108, 249 (2003).

    Article  Google Scholar 

  2. J. Hay: Introduction to instrumented indentation testing. Exp. Tech. 33, 66 (2009).

    Article  Google Scholar 

  3. M. Dao, N. Chollacoop, K.J. Van Vliet, T.A. Venkatesh, and S. Suresh: Computational modeling of the forward and reverse problems in instrumented sharp indentation. Acta Mater. 49, 3899 (2001).

    Article  CAS  Google Scholar 

  4. J.M. Antunes, J.V. Fernandes, L.F. Menezes, and B.M. Chaparro: A new approach for reverse analyses in depth-sensing indentation using numerical simulation. Acta Mater. 55, 69 (2007).

    Article  CAS  Google Scholar 

  5. M. Mata, M. Anglada, and J. Alcalá: Contact deformation regimes around sharp indentations and the concept of the characteristic strain. J. Mater. Res. 17, 964 (2002).

    Article  CAS  Google Scholar 

  6. G.R. Anstis, P. Chantikul, B.R. Lawn, and D.B. Marshall: A critical evaluation of indentation techniques for measuring fracture toughness: I, direct crack measurements. J. Am. Ceram. Soc. 64, 533 (1981).

    Article  CAS  Google Scholar 

  7. J.S. Field, M.V. Swain, and R.D. Dukino: Determination of fracture toughness from the extra penetration produced by indentation-induced pop-in. J. Mater. Res. 18, 1412 (2003).

    Article  CAS  Google Scholar 

  8. Y.P. Cao and J. Lu: A new method to extract the plastic properties of metal materials from an instrumented spherical indentation loading curve. Acta Mater. 52, 4023 (2004).

    Article  CAS  Google Scholar 

  9. M.T. Attaf: Connection between the loading curve models in elastoplastic indentation. Mater. Lett. 58, 3491 (2004).

    Article  CAS  Google Scholar 

  10. K.K. Jha, N. Suksawang, and A. Agarwal: Analytical method for the determination of indenter constants used in the analysis of nanoindentation loading curves. Scr. Mater. 63, 281 (2010).

    Article  CAS  Google Scholar 

  11. D. Chicot and D. Mercier: Improvement in depth-sensing indentation to calculate the universal hardness on the entire loading curve. Mech. Mater. 40, 171 (2008).

    Article  Google Scholar 

  12. D. Chicot, L. Gil, K. Silva, F. Roudet, E.S. Puchi-Cabrera, M.H. Staia, and D.G. Teer: Thin film hardness determination using indentation loading curve modelling. Thin Solid Films 518, 5565 (2010).

    Article  CAS  Google Scholar 

  13. K. Zeng and C-h. Chiu: An analysis of load–penetration curves from instrumented indentation. Acta Mater. 49, 3539 (2001).

    Article  CAS  Google Scholar 

  14. J. Gong, H. Miao, and Z. Peng: A new function for the description of the nanoindentation unloading data. Scr. Mater. 49, 93 (2003).

    Article  CAS  Google Scholar 

  15. W.C. Oliver and G.M. Pharr: An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments. J. Mater. Res. 7, 1564 (1992).

    Article  CAS  Google Scholar 

  16. M.F. Doerner and W.D. Nix: A method for interpreting the data from depth-sensing indentation instruments. J. Mater. Res. 1, 601 (1986).

    Article  Google Scholar 

  17. J. Gubicza, A. Juhász, P. Tasnádi, P. Arató, and G. Vörös: Determination of the hardness and elastic modulus from continuous Vickers indentation testing. J. Mater. Sci. 31, 3109 (1996).

    Article  CAS  Google Scholar 

  18. M. Yetna N’Jock, F. Roudet, M. Idriss, O. Bartier, and D. Chicot: Work-of-indentation coupled to contact stiffness for calculating elastic modulus by instrumented indentation. Mech. Mater. 94, 170 (2016).

    Article  Google Scholar 

  19. K.K. Jha, N. Suksawang, and A. Agarwal: A new insight into the work-of-indentation approach used in the evaluation of material’s hardness from nanoindentation measurement with Berkovich indenter. Comput. Mater. Sci. 85, 32 (2014).

    Article  Google Scholar 

  20. W.C. Oliver and G.M. Pharr: Measurement of hardness and elastic modulus by instrumented indentation: Advances in understanding and refinements to methodology. J. Mater. Res. 19, 3 (2004).

    Article  CAS  Google Scholar 

  21. G.M. Pharr and A. Bolshakov: Understanding nanoindentation unloading curves. J. Mater. Res. 17, 2660 (2002).

    Article  CAS  Google Scholar 

  22. J.L. Loubet, M. Bauer, A. Tonck, S. Bec, and B. Gauthier-Manuel: Nanoindentation with a Surface Force Apparatus, M. Nastasi et al., eds. (Springer, Dordrecht, 1993); p. 429.

    Google Scholar 

  23. G. Hochstetter, A. Jimenez, and J.L. Loubet: Strain-rate effects on hardness of glassy polymers in the nanoscale range. Comparison between quasi-static and continuous stiffness measurements. J. Macromol. Sci., Part B: Phys. 38, 681 (1999).

    Article  Google Scholar 

  24. P.R. Bevington and D.K. Robinson: Data Reduction and Error Analysis for the Physical Sciences (McGraw-Hill, New York, 2003).

    Google Scholar 

  25. L.C. Brown and P. Mac Berthouex: Statistics for Environmental Engineers (CRC Press, Boca Raton, 2002).

    Google Scholar 

  26. K. Smyth: Nonlinear Regression in Encyclopedia of Environmetrics, A.H. El-Shaarawi and W.W. Piegorsch, eds. (Wiley, New York, 2002).

    Google Scholar 

  27. 4.1.4.2. Nonlinear Least Squares Regression. [Online]. Available at: http://www.itl.nist.gov/div898/handbook/pmd/section1/pmd142.htm (accessed: 13-Aug-2016).

  28. K. Madsen, H.B. Nielsen, and O. Tingleff: Methods for non-linear least squares problems. In Informatics and Mathematical Modeling (Technical University of Denmark, Kongens Lyngby, 2004).

    Google Scholar 

  29. S. Gratton, A.S. Lawless, and N.K. Nichols: Approximate Gauss-Newton methods for nonlinear least squares problems. SIAM J. Optim. 18, 106 (2007).

    Article  Google Scholar 

  30. D.J. Whitehouse: Handbook of Surface and Nanometrology, 2nd ed. (CRC Press, Boca Raton, 2010).

    Book  Google Scholar 

  31. A.C. Fischer-Cripps: Critical review of analysis and interpretation of nanoindentation test data. Surf. Coat. Technol. 200, 4153 (2006).

    Article  CAS  Google Scholar 

  32. J. Menčík and M.V. Swain: Errors associated with depth-sensing microindentation tests. J. Mater. Res. 10, 1491 (1995).

    Article  Google Scholar 

  33. A. Fischer-Cripps: A review of analysis methods for sub-micron indentation testing. Vacuum 58, 569 (2000).

    Article  CAS  Google Scholar 

  34. C.A. Peters: Statistics for analysis of experimental data. In Environ. Eng. Process. Lab. Man. (S. E. Powers, Champaign, 2001); p. 1–25.

    Google Scholar 

  35. L.N. Trefethen and D. Bau, III: Numerical Linear Algebra (SIAM, Philadelphia, 1997).

    Book  Google Scholar 

  36. J. Erhel, N. Nassif, and P. Bernard: Calcul matriciel et systèmes linéaires (INSA Rennes, Rennes, 2012).

    Google Scholar 

  37. M. Sofroniou and G. Spaletta: Precise numerical computation. J. Log. Algebr. Program. 64, 113 (2005).

    Article  Google Scholar 

  38. “JCGM 101:2008-Supplement 1 to the ‘Guide to the Expression of Uncertainty in Measurement’-Propagation of distributions using a Monte Carlo method.” [Online]. Available: http://www.bipm.org/en/publications/guides/gum.html (accessed: 27-Feb-2017).

  39. “ISO 14577-1:2015-Metallic materials—Instrumented indentation test for hardness and materials parameters—Part 1: Test method,” ISO. [Online]. Available: http://www.iso.org/iso/home/store/catalogue_ics/catalogue_detail_ics.htm?csnumber=56626 (accessed: 04-Sep-2016).

  40. A. Iost, G. Guillemot, Y. Rudermann, and M. Bigerelle: A comparison of models for predicting the true hardness of thin films. Thin Solid Films 524, 229 (2012).

    Article  CAS  Google Scholar 

  41. J. Isselin, A. Iost, J. Golek, D. Najjar, and M. Bigerelle: Assessment of the constitutive law by inverse methodology: Small punch test and hardness. J. Nucl. Mater. 352, 97 (2006).

    Article  CAS  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Univ. Lille, FRE 3723—LML—Laboratoire de Mécanique de Lille, Lille, F-59000, France

    Stephania Kossman & Didier Chicot

  2. Arts et Métiers ParisTech, MSMP, Lille, 59800, France

    Stephania Kossman, Thierry Coorevits & Alain Iost

Authors
  1. Stephania Kossman
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Thierry Coorevits
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Alain Iost
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Didier Chicot
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Stephania Kossman.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kossman, S., Coorevits, T., Iost, A. et al. A new approach of the Oliver and Pharr model to fit the unloading curve from instrumented indentation testing. Journal of Materials Research 32, 2230–2240 (2017). https://doi.org/10.1557/jmr.2017.120

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1557/jmr.2017.120

Search

Navigation