Skip to main content
SpringerLink
Log in

An expanding cavity model incorporating pile-up and sink-in effects

  • Published:
Journal of Materials Research Aims and scope Submit manuscript

Abstract

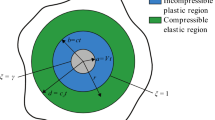
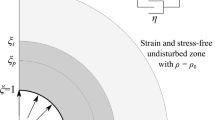
A new expanding cavity model (ECM) for describing conical indentation of elastic-ideally plastic material is developed. For the proposed ECM, it is assumed that the volume of material displaced by the indenter is equal to the volume loss, due to elastic deformation, in the material and depends on the pile-up or sink-in. It was shown that the proposed ECM matches very well numerical data in the final portion of the transition regime for which the contact pressure lies between approximately 2.5Y and 3Y. For material of large E/Y ratio, the new ECM also provides results which are very close to the numerical data in the plastic-similarity regime (regime in which Cf = 3). For material of smaller E/Y ratio, the proposed ECM gives better results than the Johnson’s ECM because pile-up or sink-in is taken into account.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

FIG. 1.
FIG. 2.
FIG. 3.
FIG. 4.
FIG. 5.
FIG. 6.
FIG. 7.
FIG. 8.
FIG. 9.

Similar content being viewed by others

References

  1. A.E.H. Love: Boussinesq’s problem for a rigid cone. Q. J. Math. 10, 161 (1939).

    Article  Google Scholar 

  2. K.L. Johnson: Contact Mechanics (Cambridge University Press, Cambridge, England, 1985), pp. 171.

    Book  Google Scholar 

  3. D. Tabor: The Hardness of Metals (Clarendon Press, Oxford, England, 1951), pp. 101.

    Google Scholar 

  4. M. Mata and J. Alcala: Mechanical property evaluation through sharp indentations in elastoplastic and fully plastic contact regimes. J. Mater. Res. 18, 1705 (2003).

    Article  CAS  Google Scholar 

  5. D.M. Marsh: Plastic flow in glass. Proc. R. Soc. London, Ser. A 279, 420 (1964).

    Article  Google Scholar 

  6. X-L. Gao: New expanding cavity model for indentation hardness including strain-hardening and indentation size effects. J. Mater. Res. 21, 1317 (2006).

    Article  CAS  Google Scholar 

  7. M. Mata, O. Casals, and J. Alcala: The plastic zone size in indentation experiments: The analogy with the expansion of a spherical cavity. Int. J. Solids Struct. 43, 5994 (2006).

    Article  Google Scholar 

  8. K.L. Johnson: The correlation of indentation experiments. J. Mech. Phys. Solids 18, 115 (1970).

    Article  Google Scholar 

  9. R. Hill: The Mathematical Theory of Plasticity (Oxford University Press, London, England, 1950).

    Google Scholar 

  10. C.J. Studman, M.A. Moore, and S.E. Jones: On the correlation of indentation experiments. J. Phys. D: Appl. Phys. 10, 949 (1977).

    Article  Google Scholar 

  11. S.S. Chiang, D.B. Marshall, and A.G. Evans: The response of solids to elastic/plastic indentation. I. Stresses and residual stresses. J. Appl. Phys. 53, 298 (1982).

    Article  CAS  Google Scholar 

  12. G. Feng, S. Qu, Y. Huang, and W.D. Nix: An analytical expression for the stress field around an elastoplastic indentation/contact. Acta Mater. 55, 2929 (2007).

    Article  CAS  Google Scholar 

  13. E.H. Yoffe: Elastic stress fields caused by indenting brittle materials. Philos. Mag. A 46, 617 (1982).

    Article  CAS  Google Scholar 

  14. A.C. Fischer-Cripps: Elastic–plastic behaviour in materials loaded with a spherical indenter. J. Mater. Sci. 32, 727 (1997).

    Article  CAS  Google Scholar 

  15. D. Kramer, H. Huang, M. Kriese, J. Robach, J. Nelson, A. Wright, D. Bahr, and W.W. Gerberich: Yield strength predictions from the plastic zone around nanocontacts. Acta Mater. 47, 333 (1999).

    Article  CAS  Google Scholar 

  16. X. Hernot and F. Pichot: Influence du coefficient de Poisson sur les régimes d’indentation sphérique. Mat. Tech. 96, 31 (2009).

    Article  Google Scholar 

  17. O. Bartier and X. Hernot: Etude des régimes de déformation de matériaux élastiques parfaitement plastiques au cours de l’indentation parabolique et sphérique. Mat. Tech. 96, 20 (2009).

    Google Scholar 

  18. J. Alcala, A.C. Barone, and M. Anglada: The influence of plastic hardening on surface deformation modes around Vickers and spherical indents. Acta Mater. 48, 3451 (2000).

    Article  CAS  Google Scholar 

  19. E. Felder: Analytical correlation of indentation experiments. Philos. Mag. 86, 5239 (2006).

    Article  CAS  Google Scholar 

  20. S. Malherbe, S. Benayoun, S. Morel, and A. Iost: Caractérisation mécanique de matériaux élastoplastiques—utilisation d’indenteurs axisymétriques. Mater. Tech. 93, 213 (2005).

    Article  Google Scholar 

  21. H. Pelletier: Étude de la formation du bourrelet autour des empreintes de nanoindentation. Mater. Tech. 93, 229 (2005).

    Article  CAS  Google Scholar 

  22. W. Zielinski, H. Huang, and W.W. Gerberich: Microscopy and microindentation mechanics of single crystal Fe-3 wt. % Si: Part II. TEM of the indentation plastic zone. J. Mater. Res. 8, 1300 (1993).

    Article  CAS  Google Scholar 

  23. M. Mata and J. Alcala: The role of friction on sharp indentation. J. Mech. Phys. Solids 52, 145 (2004).

    Article  Google Scholar 

  24. X-L. Gao: An expanding cavity model incorporating strain-hardening and indentation size effects. Int. J. Solids Struct. 43, 6615 (2006).

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. L.A.R.M.A.U.R-Indentation, E.A. 42.82, Université de Rennes 1, 35402, Rennes Cedex, France

    Xavier Hernot & Olivier Bartier

Authors
  1. Xavier Hernot
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Olivier Bartier
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Xavier Hernot.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Hernot, X., Bartier, O. An expanding cavity model incorporating pile-up and sink-in effects. Journal of Materials Research 27, 132–140 (2012). https://doi.org/10.1557/jmr.2011.394

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1557/jmr.2011.394

Search

Navigation