Abstract
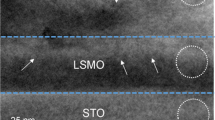
In this work, epitaxial (001) BiFeO3 thin films were deposited on SrTiO3 and TbScO3 single-crystal substrates and analyzed with high-resolution x-ray diffraction—reciprocal space mapping. A basic method was developed to extract structural details of the as-grown BiFeO3 film, including (i) epitaxial strain, (ii) ferroelastic domains, and (iii) lattice rotations. After demonstrating the method, extrinsic distortions at vertical twin walls were determined for specific BiFeO3 heterostructures. A relatively large distortion (0.20° ± 0.08°) was measured in a multidomain (12) and incoherent film, while a nearly intrinsic distortion (0.04° ± 0.03°) was measured in a two-domain coherent film. This work offers insights into the structure of multiferroic BiFeO3 thin films with a general approach that is appropriate for low symmetry epitaxial heterostructures.








Similar content being viewed by others
REFERENCES
F. Kubel and H. Schmid: Growth, twinning and etch figures of ferroelectric ferroelastic dendritic BiFeO3 single domain crystals. J. Cryst. Growth 129, 515 (1993).
R.R. Das, D.M. Kim, S.H. Baek, C.B. Eom, F. Zavaliche, S.Y. Yang, R. Ramesh, Y.B. Chen, X.Q. Pan, X. Ke, M.S. Rzchowski, and S.K. Streiffer: Synthesis and ferroelectric properties of epitaxial BiFeO3 thin films grown by sputtering. Appl. Phys. Lett. 88, 242904 (2006).
J.F. Ihlefeld, A. Kumar, V. Gopalan, D.G. Schlom, Y.B. Chen, X.Q. Pan, T. Heeg, J. Schubert, X. Ke, P. Schiffer, J. Orenstein, L.W. Martin, Y.H. Chu, and R. Ramesh: Adsorption-controlled molecular-beam epitaxial growth of BiFeO3. Appl. Phys. Lett. 91, 142908 (2007).
J. Wang, J.B. Neaton, H. Zheng, V. Nagarajan, S.B. Ogale, B. Liu, D. Viehland, V. Vaithyanathan, D.G. Schlom, U.V. Waghmare, N.A. Spaldin, K.M. Rabe, M. Wuttig, and R. Ramesh: Epitaxial BiFeO3 multiferroic thin film heterostructures. Science 299, 1719 (2003).
S. Bueble, K. Knorr, E. Brecht, and W.W. Schmahl: Influence of the ferroelastic twin domain structure on the {100} surface morphology of LaAlO3 HTSC substrates. Surf. Sci. 400, 345 (1998).
D.L. Corker, A.M. Glazer, R.W. Whatmore, A. Stallard, and F. Fauth: A neutron diffraction investigation into the rhombohedral phases of the perovskite series PbZr1-xTixO3. J. Phys. Condes. Matter 10, 6251 (1998).
F. Kubel and H. Schmid: Structure of a ferroelectric and ferroelastic monodomain crystal of the perovskite BiFeO3. Acta Crystallogr., Sect. B: Struct. Commun. 46, 698 (1990).
V. Gopalan, V. Dierolf, and D.A. Scrymgeour: Defect-domain wall interactions in trigonal ferroelectrics. Annu. Rev. Mater. Res. 37, 449 (2007).
K.R. Locherer, S.A. Hayward, P.J. Hirst, J. Chrosch, M. Yeadon, J.S. Abell, and E.K.H. Salje: X-ray analysis of mesoscopic twin structures. Philos. Trans. R. Soc. London, Ser. A 354, 2815 (1996).
A. Schilling, T.B. Adams, R.M. Bowman, J.M. Gregg, G. Catalan, and J.F. Scott: Scaling of domain periodicity with thickness measured in BaTiO3 single crystal lamellae and comparison with other ferroics. Phys. Rev. B 74, 024115 (2006).
S.Y. Yang, J. Seidel, S.J. Byrnes, P. Shafer, C.H. Yang, M.D. Rossell, P. Yu, Y.H. Chu, J.F. Scott, J.W. Ager, L.W. Martin, and R. Ramesh: Above-bandgap voltages from ferroelectric photovoltaic devices. Nat. Nanotechnol. 5, 143 (2010).
B. Velickov, V. Kahlenberg, R. Bertram, and R. Uecker: Redetermination of terbium scandate, revealing a defect-type perovskite derivative. Acta Crystallogr., Sect. E: Struct. Rep. Online 64, I79 (2008).
A.M. Glazer: Classification of tilted octahedra in perovskites. Acta Cryst. B28, 3384 (1972).
H.W. Jang, D. Ortiz, S.H. Baek, C.M. Folkman, R.R. Das, P. Shafer, Y. Chen, C.T. Nelson, X. Pan, R. Ramesh, and C.B. Eom: Domain engineering for enhanced ferroelectric properties of epitaxial (001) BiFeO3 thin films. Adv. Mater. 21, 817 (2009).
G.Y. Xu, H. Hiraka, G. Shirane, J.F. Li, J.L. Wang, and D. Viehland: Low symmetry phase in (001) BiFeO3 epitaxial constrained thin films. Appl. Phys. Lett. 86, 182905 (2005).
Y.H. Chu, M.P. Cruz, C.H. Yang, L.W. Martin, P.L. Yang, J.X. Zhang, K. Lee, P. Yu, L.Q. Chen, and R. Ramesh: Domain control in mulfiferroic BiFeO3 through substrate vicinality. Adv. Mater. 19, 2662 (2007).
A. Kopal, T. Bahnik, and J. Fousek: Domain formation in thin ferroelectric films: The role of depolarization energy. Ferroelectrics 202, 267 (1997).
C.J.M. Daumont, S. Farokhipoor, A. Ferri, J.C. Wojdel, J. Iniguez, B.J. Kooi, and B. Noheda: Tuning the atomic and domain structure of epitaxial films of multiferroic BiFeO3. Phys. Rev. B 81, 144115 (2010).
H.J. Liu, P. Yang, K. Yao, and J. Wang: Twinning rotation and ferroelectric behavior of epitaxial BiFeO3 (001) thin film. Appl. Phys. Lett. 96, (2010).
K. Saito, A. Ulyanenkov, V. Grossmann, H. Ress, L. Bruegemann, H. Ohta, T. Kurosawa, S. Ueki, and H. Funakubo: Structural characterization of BiFeO3 thin films by reciprocal space mapping. Jpn. J. Appl. Phys. 1 45, 7311 (2006).
D.G. Schlom, L.Q. Chen, C.B. Eom, K.M. Rabe, S.K. Streiffer, and J.M. Triscone: Strain tuning of ferroelectric thin films. Annu. Rev. Mater. Res. 37, 589 (2007).
C.M. Folkman, S.H. Baek, H.W. Jang, C.B. Eom, C.T. Nelson, X.Q. Pan, Y.L. Li, L.Q. Chen, A. Kumar, V. Gopalan, and S.K. Streiffer: Stripe domain structure in epitaxial (001) BiFeO3 thin films on orthorhombic TbScO3 substrate. Appl. Phys. Lett. 94, 251911 (2009).
Y.H. Chu, Q. He, C.H. Yang, P. Yu, L.W. Martin, P. Shafer, and R. Ramesh: Nanoscale control of domain architectures in BiFeO3 thin films. Nano Lett. 9, 1726 (2009).
J.D. Bucci, B.K. Robertso, and W.J. James: Precision determination of lattice parameters and coefficients of thermal expansion of BiFeO3. J. Appl. Cryst. 5, 187 (1972).
H.W. Jang, D.O.S-H. Baek, C.M. Folkman, R.R. Das, P. Shafer, Y. Chen, C.T. Nelson, X.Q. Pan, R. Ramesh, and C.B. Eom: Two-variant stripe domains in BiFeO3 films. Adv. Mater. 21, 1 (2009).
H. Nagai: Anisotropic bending during epitaxial-growth of mixed-crystals on Gaas substrate. J. Appl. Phys. 43, 4254 (1972).
J.E. Ayers, S.K. Ghandhi, and L.J. Schowalter: Crystallographic tilting of heteroepitaxial layers. J. Cryst. Growth 113, 430 (1991).
S.K. Streiffer, C.B. Parker, A.E. Romanov, M.J. Lefevre, L. Zhao, J.S. Speck, W. Pompe, C.M. Foster, and G.R. Bai: Domain patterns in epitaxial rhombohedral ferroelectric films. I. Geometry and experiments. J. Appl. Phys. 83, 2742 (1998).
A.E. Romanov, M.J. Lefevre, J.S. Speck, W. Pompe, S.K. Streiffer, and C.M. Foster: Domain pattern formation in epitaxial rhombohedral ferroelectric films. II. Interfacial defects and energetics. J. Appl. Phys. 83, 2754 (1998).
G. Catalan, I. Lukyanchuk, A. Schilling, J.M. Gregg, and J.F. Scott: Effect of wall thickness on the ferroelastic domain size of BaTiO3. J. Mater. Sci. 44, 5307 (2009).
U. Shmueli: International Tables for Crystallography: 1. General Relationships and Techniques, 2nd ed. (Kluwer Academic Publisher, Dordrecht, Netherlands, 2005), pp. 2–7.
R.P. Liferovich and R.H. Mitchell: A structural study of ternary lanthanide orthoscandate perovskites. J. Solid State Chem. 177, 2188 (2004).
B. Velickov, V. Kahlenberg, R. Bertram, and M. Bernhagen: Crystal chemistry of GdScO3, DyScO3, SmScO3 and NdScO3. Z. Kristallogr. 222, 466 (2007).
ACKNOWLEDGMENTS
We thank Dr. Dillon Fong at Argonne National Labs for reading of the manuscript and providing constructive comments. This work is supported by the Army Research Office under Grant No. W911NF-10-1-0362.
Author information
Authors and Affiliations
Corresponding author
APPENDIX
APPENDIX
The bulk real space structures of the BiFeO3 film and the substrates were described with individual sets of basis vectors in a single Cartesian coordinate system (see subcells in Fig. 1). After defining the heterostructure in real space, the basis vectors were transformed to reciprocal space using standard Gibb’s relations.31 The real space lattice corresponding to the substrates was fixed. In contrast, the real space lattice of the BiFeO3 film was matched to the data considering the following parameters: subcell definition (ap, bp, cp, αp, βp, and γp) and parameters associated with structural variants (R), specifically (r1, r2, r3, or r4) and lattice rotations (\(\hat k\), ω).
The substrate lattice (Fig. 1) transformation matrices were defined for SrTiO3 with a = 3.905 Å and TbScO3 with am = cm = \({{\sqrt {a_{\rm{o}}^2 + b_{\rm{o}}^2 } } \mathord{\left/ {\vphantom {{\sqrt {a_{\rm{o}}^2 + b_{\rm{o}}^2 } } 2}} \right. \kern-\nulldelimiterspace} 2}\) = 3.953 Å, bm = \({{c_{\rm{o}} } \mathord{\left/ {\vphantom {{c_{\rm{o}} } 2}} \right. \kern-\nulldelimiterspace} 2}\) = 3.957 Å, and βm = \(2\tan ^{ - 1} \left( {{{a_{\rm{o}} } \mathord{\left/ {\vphantom {{a_{\rm{o}} } {b_{\rm{o}} }}} \right. \kern-\nulldelimiterspace} {b_{\rm{o}} }}} \right)\) = 87.243°.123233

A transformation matrix was also used to define the BiFeO3 film subcell (F) although in contrast to the substrates, the lattice parameters ap, bp, cp, and intercell angles αp, βp, and γp were made flexible as to fit the experimental data (general triclinic structure).

where,



The expressions for F were geometrically derived assuming the subcell initially lies flat on the crystallographic growth surface (F[2,3] = F[1,3] = 0) and equally spaced from the [100] and [010] axes.
Four ferroelastic variations are in a rhombohedral system which quadruples the number of independent lattices that must be considered. These were accounted for using separate matrices, r1–4, where each may be visualized as a stretching of the subcell along the <111> diagonals (Fig. 1).28

Additionally, structural variants (R) were considered to account for the possibility of lattice rotations. This was accomplished considering the ferroelastic variants (r1–4) and a rotation matrix.31

Here ω is the magnitude of the rotation about a unit vector \(\hat k\) = [k1, k2, k3]. Here discussion was limited to ωf and ωd, which are notations used in the text to describe lattice rotation of the entire film due to miscut and individual ferroelastic domains due to twin walls, respectively.
At this point, transformation of all the individual real space lattices of the film and substrate to reciprocal space (H K L) was performed using the standard Gibb’s relations generating respective reciprocal lattices in the same coordinate system (Fig. 1).31
To compare with the measured 2D RSM data, the nearest scattering vector GHKL of each reciprocal lattice was projected onto the exact plane measured in reciprocal space. The projected GProj was calculated with,
where P defines the measured plane in reciprocal space (P/ is the transpose). For {002} and {103} reflections,

and for {113} reflections,

A full list of reflections used in this study is given in Table II with the position equivalent bulk Bragg reflections. The Bragg reflections for single-crystal substrates were used for calibration.
Rights and permissions
About this article
Cite this article
Folkman, C.M., Baek, SH. & Eom, CB. Twin wall distortions through structural investigation of epitaxial BiFeO3 thin films. Journal of Materials Research 26, 2844–2853 (2011). https://doi.org/10.1557/jmr.2011.327
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1557/jmr.2011.327