Skip to main content

Advertisement

SpringerLink
Log in

Extended JKR theory on adhesive contact of a spherical tip onto a film on a substrate

  • Published:
Journal of Materials Research Aims and scope Submit manuscript

Abstract

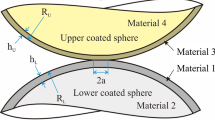
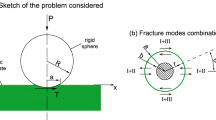
The conventional JKR theory was extended to the adhesive contact of a rigid sphere onto an elastic film perfectly bonded to a rigid substrate. An elasticity problem of axisymmetric indentation on an elastic film was revisited, in which the force–depth relations for both flat and spherical indentations were obtained in a simple form. With the obtained force–depth relations, the energy release rate at the debonding of a spherical tip from an elastic film was expressed in terms of pull-off force, elastic constants, and geometric parameters. The adhesion energy between a spherical tip and an elastic film can be measured as the critical energy release rate at the instability of debonding. This study suggests that when the critical radius of contact is larger than the thickness of an elastic film, the extended JKR theory should be used in place of the conventional JKR theory to correctly evaluate the adhesion energy between the spherical tip and the elastic film.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

FIG. 1.
FIG. 2.
FIG. 3.
FIG. 4.
FIG. 5.
FIG. 6.
FIG. 7.
FIG. 8.
FIG. 9.

Similar content being viewed by others

References

  1. K.L. Johnson, K. Kendall, and A.D. Robert: Surface energy and the contact of elastic solids. Proc. R. Soc. London, Ser. A 324, 301 (1971).

    Article  CAS  Google Scholar 

  2. K. Kendall: The adhesion and surface energy of elastic solids. J. Phys. D: Appl. Phys. 4, 1186 (1971).

    Article  Google Scholar 

  3. B.V. Derjaguin, V.M. Muller, and Y.P. Toporov: Effect of contact deformations on the adhesion of particles. J. Colloid Interface Sci. 53, 314 (1975).

    Article  CAS  Google Scholar 

  4. D. Tabor: Surface forces and surface interactions. J. Colloid Interface Sci. 58, 1 (1977).

    Article  Google Scholar 

  5. D. Maugis: Adhesion of spheres: The JKR-DMT transition using a Dugdale model. J. Colloid Interface Sci. 150, 243 (1992).

    Article  CAS  Google Scholar 

  6. D. Maugis: Contact, Adhesion and Rupture of Elastic Solids (Springer Series in Solid-State Sciences, New York, 2000).

    Book  Google Scholar 

  7. E. Barthel: Adhesive elastic contacts: JKR and more. J. Phys. D: Appl. Phys. 41, 163001 (2008).

    Article  Google Scholar 

  8. N.N. Lebedev and Ia.S. Ufliand: Axisymmetric contact problem for an elastic layer. J. Appl. Math. Mech. 22, 320 (1958).

    Article  Google Scholar 

  9. R.S. Dhaliwal: Punch problem for an elastic layer overlying an elastic foundation. Int. J. Eng. Sci. 8, 273 (1970).

    Article  Google Scholar 

  10. W.C. Hayes, L.M. Keer, G. Herrmann, and L.F. Mockros: A mathematical analysis for indentation tests of articular cartilage. J. Biomech. 5, 541 (1972).

    Article  CAS  Google Scholar 

  11. H.Y. Yu, S.C. Sanday, and B.B. Rath: The effect of substrate on the elastic properties of films determined by the indentation test-axisymmetric Boussinesq problem. J. Mech. Phys. Solids 38, 745 (1990).

    Article  Google Scholar 

  12. F. Yang: Indentation of an incompressible elastic film. Mech. Mater. 30, 275 (1998).

    Article  Google Scholar 

  13. F. Yang: Thickness effect on the indentation of an elastic layer. Mater. Sci. Eng., A 358, 226 (2003).

    Article  Google Scholar 

  14. S.T. Choi, S.R. Lee, and Y.Y. Earmme: Measurement of time-dependent adhesion between a polymer film and a flat indenter tip. J. Phys. D: Appl. Phys. 41, 074023 (2008).

    Article  Google Scholar 

  15. P. Mary, A. Chateauminois, and C. Fretigny: Deformation of elastic coatings in adhesive contacts with spherical probes. J. Phys. D: Appl. Phys. 39, 3665 (2006).

    Article  CAS  Google Scholar 

  16. I. Sridhar, K.L. Johnson, and N.A. Fleck: Adhesion mechanics of the surface force apparatus. J. Phys. D: Appl. Phys. 30, 1710 (1997).

    Article  CAS  Google Scholar 

  17. K.L. Johnson and I. Sridhar: Adhesion between a spherical indenter and an elastic solid with a compliant elastic coating. J. Phys. D: Appl. Phys. 34, 683 (2001).

    Article  CAS  Google Scholar 

  18. I. Sridhar and K.L. Johnson: On the adhesion mechanics of multi-layer elastic systems. Surf. Coat. Tech. 167, 181 (2003).

    Article  CAS  Google Scholar 

  19. I. Sridhar, Z.W. Zheng, and K.L. Johnson: A detailed analysis of adhesion mechanics between a compliant elastic coating and a spherical probe. J. Phys. D: Appl. Phys. 37, 2886 (2004).

    Article  CAS  Google Scholar 

  20. G.M.L. Gladwell: Contact Problems in the Classical Theory of Elasticity (Sijthoff & Noordhoff International Publishers, The Netherlands, 1980).

    Book  Google Scholar 

  21. I.N. Sneddon: The relation between load and penetration in the axisymmetric boussinesq problem for a punch of arbitrary profile. Int. J. Eng. Sci. 3, 47 (1965).

    Article  Google Scholar 

  22. H. R. Hertz: Über die Berührung fester elastischer Körper (On the contact of elastic solids). J. Reine Angew. Math. 92, 156 (1882).

    Google Scholar 

  23. D. Maugis and M. Barquins: Fracture mechanics and the adherence of viscoelastic bodies. J. Phys. D: Appl. Phys. 11, 1989 (1978).

    Article  Google Scholar 

  24. R.M. Christensen: Theory of Viscoelasticity (Academic Press, New York, 1982).

    Google Scholar 

  25. G.A.C. Graham: The correspondence principle of linear viscoelasticity theory for mixed boundary value problems involving time-dependent boundary regions. Q. Appl. Math. 26, 167 (1968).

    Article  Google Scholar 

Download references

Acknowledgment

This work was supported by the 2011 Research Fund of University of Ulsan.

Author information

Authors and Affiliations

  1. School of Mechanical Engineering, University of Ulsan, Ulsan, 680-749, Republic of Korea

    Seung Tae Choi

Authors
  1. Seung Tae Choi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Seung Tae Choi.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Choi, S.T. Extended JKR theory on adhesive contact of a spherical tip onto a film on a substrate. Journal of Materials Research 27, 113–120 (2012). https://doi.org/10.1557/jmr.2011.324

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1557/jmr.2011.324

Search

Navigation