Skip to main content
SpringerLink
Log in

Domain switch toughening in polycrystalline ferroelectrics

  • Outstanding Meeting Papers: Articles
  • Published:
Journal of Materials Research Aims and scope Submit manuscript

Abstract

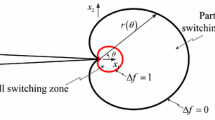
Mode I steady crack growth was analyzed to determine the toughening due to domain switching in ferroelectric ceramics. A multi-axial, electromechanically coupled, incremental constitutive theory is applied to model the material behavior of the ferroelectric ceramic. The constitutive law is then implemented within the finite element method to study steady crack growth. The effects of mechanical and electrical poling on the fracture toughness are investigated. Results for the predicted fracture toughness, remanent strain distributions, and domain switching zone shapes and sizes are presented. Finally, the model predictions are discussed in comparison discrete switching models and to experimental observations.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. G.G. Pisarenko, V.M. Chusko and S.P. Kovalev: Anisotropy of fracture toughness of piezoelectric ceramics. J. Am. Ceram. Soc. 68, 259 (1985).

    Article  CAS  Google Scholar 

  2. K. Metha and A.V. Virkar: Fracture mechanisms in ferroelectric-ferroelastic lead zirconate titanate (Zr:Ti = 0.54:0.46) ceramics. J. Am. Ceram. Soc. 73, 567 (1990).

    Article  Google Scholar 

  3. A.G. Tobin and Y.E. Pak: Effect of electric fields on fracture behavior of PZT ceramics. Proc. SPIE 1916, 78 (1993).

    Article  CAS  Google Scholar 

  4. H. Wang and R.N. Singh: Crack propagation in piezoelectric ceramics: Effects of applied electric field. J. Appl. Phys. 81, 7471 (1997).

    Article  CAS  Google Scholar 

  5. G.A. Schneider and V. Heyer: Influence of the electric field on Vickers indentation crack growth in BaTiO3. J. Eur. Ceram. Soc. 19, 1299 (1999).

    Article  CAS  Google Scholar 

  6. S.L. Lucato, J. Lindner, D.C. Lupascu and J. Rödel: Influence of electrical and geometrical boundary conditions on crack growth in PZT. Key Eng. Mater. 206–213, 609 (2002).

    Google Scholar 

  7. W. Yang, F. Fang and M. Tao: Critical role of domain switching on the fracture toughness of poled ferroelectrics. Int. J. Solids Struct. 38, 2203 (2001).

    Article  Google Scholar 

  8. S. Hackemann and W. Pfeiffer: Domain switching in process zones of PZT: Characterization by micro diffraction and fracture mechanical methods. J. Eur. Ceram. Soc. 23, 141 (2003).

    Article  CAS  Google Scholar 

  9. M. Kamlah: Ferroelectric and ferroelastic piezoceramics—modeling and electromechanical hysteresis phenomena. Continuum Mech. Thermodyn. 13, 219 (2001).

    Article  CAS  Google Scholar 

  10. C.M. Landis: Non-linear constitutive modeling of ferroelectrics. Curr. Opin. Solid State Mater. Sci. 8, 59 (2004).

    Article  CAS  Google Scholar 

  11. C.M. Landis: Fully coupled, multi-axial, symmetric constitutive laws for polycrystalline ferroelectric ceramics. J. Mech. Phys. Solids 50, 127 (2002).

    Article  Google Scholar 

  12. C.M. Landis: On the strain saturation conditions for polycrystalline ferroelastic materials. J. Appl. Mech. 70, 470 (2003).

    Article  Google Scholar 

  13. C.M. Landis, J. Wang and J. Sheng: Micro-electromechanical determination of the possible remanent strain and polarization states in polycrystalline ferroelectrics and implications for phenomenological constitutive theories. J. Intell. Mater. Syst. Struct. 15, 513 (2004).

    Article  Google Scholar 

  14. J.E. Huber, N.A. Fleck, C.M. Landis and R.M. McMeeking: A constitutive model for ferroelectric polycrystals. J. Mech. Phys. Solids 47, 1663 (1999).

    Article  CAS  Google Scholar 

  15. C.S. Lynch: The effect of uniaxial stress on the electro-mechanical response of 8/65/35 PLZT. Acta Mater. 44, 4137 (1996).

    Article  CAS  Google Scholar 

  16. C.M. Landis: On the fracture toughness of ferroelastic materials. J. Mech. Phys. Solids 51, 1347 (2003).

    Article  Google Scholar 

  17. C.M. Landis: On the fracture toughness anisotropy of mechanically poled ferroelectric ceramics. Int. J. Fract. 126, 1 (2004).

    Article  Google Scholar 

  18. J. Wang and C.M. Landis: On the fracture toughness of ferroelectric ceramics with electric field applied parallel to the crack front. Acta Mater. 52, 3435 (2004).

    Article  CAS  Google Scholar 

  19. C.M. Landis: In-plane complex potentials for a special class of materials with degenerate piezoelectric properties. Int. J. Solids Struct. 41, 695 (2004).

    Article  Google Scholar 

  20. J.W. Hutchinson “A course on nonlinear fracture mechanics,” Harvard University Report, DEAP S-8, Division of Applied Sciences (Harvard University, Cambridge, MA, 1974).

    Google Scholar 

  21. C.M. Landis: A new finite-element formulation for electromechanical boundary value problems. Int. J. Numer. Meth. Eng. 55, 613 (2002).

    Article  Google Scholar 

  22. F.Z. Li, C.F. Shih and A. Needleman: Comparison of methods for calculating energy release rates. Eng. Fract. Mech. 21, 405 (1985).

    Article  Google Scholar 

  23. C.M. Landis: Energetically consistent boundary conditions for electromechanical fracture. Int. J. Solids Struct. 41, 6291 (2004).

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering and Materials Science, Rice University, Houston, Texas, 77005, USA

    Jianxin Wang & Chad M. Landis

Authors
  1. Jianxin Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Chad M. Landis
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Chad M. Landis.

Additional information

Address all correspondence to this author.

This paper was selected as the Outstanding Meeting Paper for the 2005 MRS Spring Meeting Symposium CC Proceedings, Vol. 881E.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Wang, J., Landis, C.M. Domain switch toughening in polycrystalline ferroelectrics. Journal of Materials Research 21, 13–20 (2006). https://doi.org/10.1557/jmr.2006.0002

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1557/jmr.2006.0002

Search

Navigation