Formation and stability of the prismatic stacking faultin wurtzite (Al,Ga,In) nitrides

Abstract

The formation of the $\left\{ {1\bar 210} \right\}$ stacking fault, which has two atomic configurations in wurtzite (Ga,Al,In)N, has been investigated by high resolution electron microscopy and energetic calculations. It originates from steps at the SiC surface and it can form on a flat (0001) sapphire surface. A modified Stillinger-Weber potential was used in order to investigate the relative stability of the two atomic configurations. They have comparable energy in AlN, whereas the $1/2\left\langle {10\bar 11} \right\rangle \left\{ {1\bar 210} \right\}$ configuration is more stable in GaN and InN. In GaN layers, only the $1/2\left\langle {10\bar 11} \right\rangle \left\{ {1\bar 210} \right\}$ configuration was observed. The $1/6\left\langle {20\bar 23} \right\rangle$ configuration was found in small areas inside the AlN buffer layer where it folded rapidly to the basal plane, and when back into the prismatic plane, it took the $1/2\left\langle {10\bar 11} \right\rangle \left\{ {1\bar 210} \right\}$ atomic configuration.

Introduction

Extensive research effort is being undertaken on wide band gap of GaN based semiconductors for their very promising device possibilities. Efficient laser diodes have been fabricated for emission in the blue range[1] in layers grown on sapphire by Metal Organic Vapor Epitaxy (MOVPE). The active GaN layers contain large densities of crystallographic defects[2,3 ], among which, one finds $\left\{ {1\bar 210} \right\}$ planar defects which have recently been called double positioning boundaries (DPBs)[4,5], stacking mismatch boundaries (SMBs)[6] or inversion domain boundaries (IDBs)[7]. These faults have recently been investigated using High Resolution Electron Microscopy (HREM) and Convergent Beam Electron Diffraction (CBED), and it was shown that they are stacking faults on top of both sapphire and SiC[8-10 ]. In fact these planar defects have already been studied in the sixties and two displacement vectors have been measured by conventional microscopy[11,12 ]. In wurtzite ZnS, Blank et al[12 ] were the first to study the planar defects which folded from basal to prismatic $\left\{ {1\bar 210} \right\}$ planes, and to interpret them as stacking faults whereas other authors considered them to be thin lamella of the sphalerite phase in CdS[13]. In this work, we have investigated these faults in (Al,Ga)N epitaxial layers by HREM and modified the Stillinger-Weber[14] (SW) potential in order to analyze their stability in AlN, GaN, InN. The theoretical results were found to correlate with the HREM observations for AlN and GaN.

Results

The stacking fault atomic structure

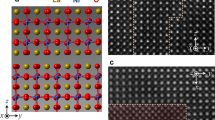
Two atomic models exist in the literature for the $\left\{ {1\bar 210} \right\}$ prismatic fault in wurtzite materials as originally characterized by conventional electron microscopy in the 60s by Drum[11 ] and Blank[12 ], respectively. Their projections are shown in figure 1 along [0001].

Figure 1

Atomic configurations of the $\left\{ {1\bar 210} \right\}$ stacking fault seen along [0001], a) The ½ $\left[ {10\bar 11} \right]$ displacement vector, b) The $1/6\left[ {20\bar 23} \right]$ stacking fault

Formation mechanisms

A. Formation on (0001) 6H-SiC surface

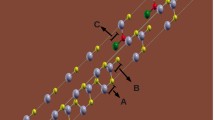
The [0001] SiC surface exhibits steps of various heights. If one ignores the mismatch along the c axis which is small, the GaN and SiC can be geometrically consid

A 6H-portion under a step can be decomposed into a faulted 2H stacking, and depending on the type of step, the decomposition may result in a displacement vector between the two crystallites which grow on the adjacent terraces (fig. 2). In fact between the two polytypes, the only displacement vectors d which can result from the decomposition are those of the hcp lattice ( the intrinsic ${I_1},{R_{I1}} = 1/6\left\langle {20\bar 23} \right\rangle ,{I_2},{R_{I2}} = 1/3\left\langle {10\bar 10} \right\rangle$ and the extrinsic E, R_E = 1/2 <0001> ). Among them, I1 and E have 1/2c component along the c axis and may lead to the formation of an extended defect in the epitaxial layer (fig. 2). The displacement vector identical to I₂ is confined in the interface and may contribute to release the misfit strain. When all the step heights are taken account, it was found that the largest fraction of the faults that will be formed are I₁ as shown in table 1

Figure 2

Generation of a prismatic stacking fault on a I1 type of step on the (0001) surface of 6H-SiC

Table 1

Type of defects forming at an interface step between 2H-GaN and 6H-SiC

B. Growth on (0001) sapphire

The continuation of the two hcp anionic lattices may be described by three types of polyhedra at the interface. They are built with oxygen (O) and nitrogen (N) at their vertices, the metal (M) at the centre: one tetrahedron (3O, M, N) that leads to upward polarity, one tetrahedron (O, M, 3N) and one octahedron (3O, M, 3N) that lead to downward polarity. All these factors are taken into account in order to analyze how the resulting translation can be accommodated in the GaN layers by the formation of planar defects in the epitaxial layer: stacking faults (SF) or inversion domains boundaries (IDB). For the wurtzite structure, three models of IDBs have been proposed[15-18 ].

B.1. Growth on a single terrace

On an oxygen terminated surface, there are four ways to build a hcp stacking of nitrogen atoms, they are related to each other by one of the three stacking fault vectors, R_SF, of the wurtzite structure (R_I1, R_I2 and R_E). Since two families of tetrahedral sites are available for the Ga³⁺ cation, this leads to eight GaN stackings linked by the operator W_CE = R_SF or W_CE = R_SF + m with opposite polarities(fig. 3). In the case of Al-terminated surface, the number of stackings is reduced to three polyhedra due to the aluminium position in the Al₂O₃ structure. The systematic analysis of the polyhedra combinations allows to determine the relative proportions of the planar defects induced by the operator W_CE. For instance, if the interface polyhedra are exclusively downward tetrahedra, the R_SF will be only R_I1, and combinations of downward tetrahedra and octahedra lead to the formation of RI1 and RI2 faults in equal proportions which may explain the formation of stacking faults inside the epitaxial layers[19-21 ].

B.2. Growth on adjacent terraces

A step, between two terraces on which two GaN islands grow, introduces a translation T_S between them. Its component along c axis can be reduced in R_E=1/2 <0001> and a residual translation T_R. The number of R_E is calculated to minimize the absolute value of this residual translation. For instance, the step between two A terraces with a height of c/3 in Al₂O₃ (0.433 nm) is equivalent in GaN to 0.835 c_GaN, or : T_S = 2R_E + T_R = T_R with T_R = - 0.165 c_GaN ≈ c_GaN/6. By considering all the steps between A or B terraces (A or B layers of the hcp stacking), the T_S translation can be written as : T_S = aR_E + T_R with a = 0 or 1 and T_R may take four values with the approximation ${2_{{C_{A{l_2}{O_3}}}}}\sim{5_{{C_{GaN}}}}$ (table. 2) : So, the operator relating adjacent terraces must involve this additional parameter, T_R :

$$2{\rm{c}}_{{\rm{Al}}_{\rm{2}} {\rm{O}}_3 } \sim5{\rm{c}}_{{\rm{GaN}}} $$

((1))

As this residual translation is never equal to c/2, it cannot be simply accommodated by the formation of prismatic stacking faults. The operator describing IDBs can be written in order to point out the c/8 translation found inside some of the models in addition to the mirror operation (1). When compared to the residual translation T_R, the introduction of the IDB containing the c/8 translation may help in minimizing the shift along c at most of the steps; it is reduced to 1/24 c_GaN[20]. Therefore, in the case of steps, the residual translation cannot be minimized by introducing a stacking fault. During epitaxial growth of GaN layers on (0001) sapphire, the occurrence of basal and prismatic stacking faults is not a straightforward result of the steps at the substrate surface. They form on coalescence of islands whose growth has been initiated with different polyhedra[20].

Table 2

Residual translation in GaN as a function of the step height in Al₂O₃

Figure3

Four of the 8 possible stacking of wurtzite (Ga,Al)N on the (0001) sapphire surface, the polyhedra configurations at the interface are shown

Relative stability

The original SW potential is short and it cannot be used in order to predict the values of the non ideal c/a ratio and the vector u which characterizes the displacement along the c axis between the two hcp sublattices in the wurtzite structure. It is unable to reach the third nearest neighbour atom which is responsible of the deviation of c/a ratio from the ideal value. We have added a Gaussian term which was fitted in order to allow the interaction potential to reach the third nearest neighbour. It is given by:

$$v_{\rm{g}} = {{\varepsilon Cexp}}\left\{ {{\rm{ - }}\left( {\left( {{\rm{d}}_{{\rm{ij}}} {\rm{ - r}}_1 } \right)/{{\delta r}}_{\rm{1}} } \right)^2 } \right\},$$

((2))

where d_ij is the bond length between atoms i and j, r₁ the center of the Gaussian is situated between the second and third neighbours distances and Δr₁ is the width of the Gaussian function. According to the magnitude of r₁ and the sign of C, it is possible to adjust the c/a ratio with respect to the ideal value. The potential obtained in the previous section is applied to investigate the atomic structure of the $\left\{ {11\bar 20} \right\}$ stacking fault. The above atomic models were taken into account with the starting configurations corresponding to the $1/6\left\langle {2\bar 203} \right\rangle$ and $1/2\left\langle {1\bar 101} \right\rangle$ stacking fault displacement vectors as discussed in the previous paragraphs. We applied the method of lattice relaxation to a set of 1984 atoms containing the defect for the two atomic models. As seen in table 3, the formation energy of each configuration depends on the compound for AlN, GaN and InN. In AlN, the two atomic configurations of the $\left\{ {11\bar 20} \right\}$ stacking fault have a comparable value of formation energy. This is in complete agreement with our HREM observations in GaN layers and in the AlN buffers²²

Table 3

Formation energy in me ${\text{V/}}\mathop {{{\text{A}}^2}}\limits^0$ ² for the relaxed atomic configurations of the $\left\{ {11\bar 20} \right\}$ prismatic stacking fault, in parenthesis are the values of reference 23

Conclusion

The two configurations of the stacking fault have already been investigated by conventional electron microscopy, one in AlN and the other in ZnS respectively. They both were found to fold easily from the basal to the prismatic plane of these wurtzite materials. In the basal plane both have the $1/6\left\langle {20\bar 23} \right\rangle$ displacement vector of the I1 stacking fault. In the $\left\{ {11\bar 20} \right\}$ plane, they differ by $1/6\left\langle {10\bar 10} \right\rangle$, which is worth less than 4% in energetic balance between the two vectors (using the b² criterion) in the three nitrides compounds.