Abstract
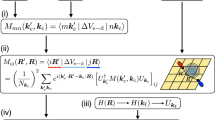
In this work, variations in electron potential are incorporated into a Kinetic Lattice Monte Carlo (KLMC) simulator and applied to dopant diffusion in silicon. To account for the effect of dopants, the charge redistribution induced by an external point charge immersed in an electron (hole) sea is solved numerically using the quantum perturbation method. The local carrier concentrations are then determined by summing contributions from all ionized dopant atoms and charged point defects, from which the Fermi level of the system is derived by the Boltzmann equation. KLMC simulations with incorporated Fermi level effects are demonstrated for charged point defect concentration as a function of Fermi level, coupled diffusion phenomenon and field effect on doping fluctuations.
Similar content being viewed by others
References
S. T. Dunham and C. D. Wu, J. Appl. Phys. 78, 2362 (1995).
M. M. Bunea and S. T. Dunham, in Semiconductor Process and Device Performance Modeling, edited by S. T. Dunham and J. Nelson, (Mater. Res. Soc. Proc. 490, Pittsburgh, PA, 1998) pp. 3–8.
P. M. Fahey, P. B. Griffin and J. D. Plummer, Rev. Mod. Phys. 61, 289 (1989).
N. W. Ashcroft and N. D. Mermin, Solid State Physics, 1st ed. (Holt, Rinehart and Wilson, 1976) pp. 342.
J. Chazalviel, Coulomb Screening by Mobile Charges: Applications to Materials Science, Chemistry, and Biology, (Birkhäuser, 1998) pp. 27–34.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Qin, Z., Dunham, S.T. Modeling Fermi Level Effects in Atomistic Simulations. MRS Online Proceedings Library 717, 38 (2002). https://doi.org/10.1557/PROC-717-C3.8
Published:
DOI: https://doi.org/10.1557/PROC-717-C3.8