Molecular Drag-Strain Coupling in Branched Polymer Melts

Abstract

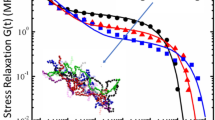
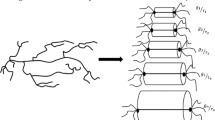
The “pom-pom” model of McLeish and Larson (J. Rheol. 42, 81, 1998) provides a simple molecular theory for the nonlinear rheology of long chain branched polymer melts. The Edwards-de Gennes tube concept is used to derive a constitutive equation for a simple branched molecule composed of two star polymers linked by a single backbone chain. A feature of this model is that the backbone section of tube can stretch up to maximum length given by the maximum entropic drag-force from the arms, after which the star arms are withdrawn into the backbone tube. This produces a sharp transition in the extensional viscosity at this maximum stretch. This unphysical feature results from an over-simplification of the behaviour near the branch points.

In this paper we introduce a simple treatment of the coupling between relaxed and unrelaxed polymer segments at branch-points. This allows for localised displacements of branch-point within a quadratic potential before maximum extension is reached. Displacing the branch-point reduces the length of arm outside the tube and so reduces in the drag on the star arms. This smoothes out the sharp transitions in extensional viscosity in the original “pom-pom” model at the cost of introducing an extra unknown parameter.

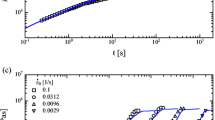
This modification improves the prediction of the nonlinear rheology of H-polymers whose molecular structure is known. Alternatively, for polymers of unknown structure such as commercial Low Density Polyethylene, the model parameters may be fitted from linear viscoelastic and uniaxial extension data, to provide predictions for the behaviour in transient nonlinear shear and planar extension. By including local branch-point displacement we find improved agreement with the data for Low-Density Polyethylene.