Skip to main content
SpringerLink
Log in

A Note on the Institution as a Nested Reasoning Structure in Terms of Bounded Cognition

  • Note
  • Published:
Evolutionary and Institutional Economics Review Aims and scope Submit manuscript

Abstract

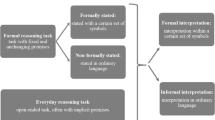
The present note discusses a new view of the institution as a nested structure of reciprocal reasoning. To explain the emergence of a Nash equilibrium, Aumann assumed common knowledge of the conjectures of agents with respect to strategy spaces. In the present note, we demonstrate that common knowledge can be defined by knowledge and infinite reasoning. However, recent studies in experimental economics, suggest that the assumption of infinite reciprocal reasoning is, in most cases, neither empirically relevant nor necessary for achieving a Nash equilibrium. Moreover, we demonstrate that reasonable states, which are composed of non-Nash equilibrium strategies, are attained only by bounded reasoning agents. Furthermore, this view of the institution is applied to examples such as Bentham’s Panopticon and the depth of reasoning in the institution is examined.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  • Aoki, M. (2001) Toward a Comparative Institutional Analysis (Comparative Institutional Analysis, 2), MIT Press.

  • - (2007) “Endogenizing institutions and institutional changes,” Journal of Institutional Economics 3.1: 1–31.

  • Aumann R. J. (1992) “Irrationality in game theory,” Economic Analysis of Markets and Games, MIT Press.

  • - (1997) “Rationality and Bounded Rationality,” Games and Economic Behavior 21: 2–14.

  • - and A. Brandenburger (1995) “Epsmetic condition for Nash equilibrium,” Econometrica 63.5: 1161–1180.

    Google Scholar 

  • Bentham, J. and J. Bowring, (1838) Works of Jeremy Bentham, Edinburgh, W. Tait.

  • Camerer, C. F., T.-H. Ho and J.-K. Chong (2004) “A Cognitive Hierarchy Model of Games,” Quartely Journal of Economics 119.3: 861–898.

    Article  Google Scholar 

  • Chwe, M. S.-Y. (2003) Rational Ritual: Culture, Coordination, and Common Knowledge, Princeton University Press.

  • Costa-Gomes, M., V. P. Crawford and B. Broseta (2001) “Cognition and Behavior in Normal-Form Games: An Experimental Study,” Econometrica 69.5: 1193–1235.

    Article  Google Scholar 

  • Gabaix, X. and D. Laibson (2000) “A Boundedly Rational Decision Algorithm,” The American Economic Review 90.2: 433–438.

    Article  Google Scholar 

  • Masumoto, G. (2000) The Lambda Game System: an approach to a meta-game (Feasibility of Theoretical Arguments of Mathematical Analysis on Computer). [http://www.hdl.handle.net/2433/25677]

  • Haruvy, E. and D. O. Stahl (2004) “Deductive versus inductive equilibrium selection: experimental results,” Journal of Economic Behavior & Organization 53: 319–331.

    Article  Google Scholar 

  • - (2007) “Equilibrium selection and bounded rationality in symmetric normal-form games,” Journal of Economic Behavior & Organization 62: 98–119.

    Article  Google Scholar 

  • Ho, T. H., C. Camerer and K. Weigelt (1998) “Iterated Dominance and Iterated Best Response in Experimental “p-Beauty Contests”,” The American Economic Review 88.4: 947–969.

    Google Scholar 

  • Fischbachera, U., S. Gachter and E. Fehr (2001) “Are people conditionally cooperative? Evidence from a public goods experiment,” Economics Letters 71: 397–404.

    Article  Google Scholar 

  • Nagel, R. (1995) “Unraveling in Guessing Games: An Experimental Study,” The American Economic Review 85.5: 1313–1326.

    Google Scholar 

  • Spiro, P. F. (2000) “The New Sovereigntists—American Exceptionalism and Its False Prophets-”, Forein Affairs, November/December.

  • Stahl, D. O. (1998) “Is step-j thinking an arbitrary modelling restriction or a fact of human nature?,” Journal of Economic Behavior & Organization 37: 33–51.

    Article  Google Scholar 

  • - and E. Haruvy “Level-n bounded rationality in two-player two-stage games,” Journal of Economic Behavior & Organization (in press).

    Article  Google Scholar 

  • - and - “Level-n bounded rationality and dominated strategies in normal-form games,” Journal of Economic Behavior & Organization (in press).

  • Kawamura, T., G. Masumoto and Y. Kobayashi Possibility of evolution about reasoning abirity in complex game, mimeo (forthcoming).

  • Victor, D. G. (2001) The Collapse of the Kyoto Protocol and the Struggle to Slow Global Warming, Princeton University Press.

  • Shinada, M. and T. Yamagishi (2007) “Punishing free riders: direct and indirect promotion of cooperation,” Evolution and Human Behavior 28.5: 330–339.

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. JSPS Research Fellow, Japan

    Tetsuya Kawamura

Authors
  1. Tetsuya Kawamura
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Tetsuya Kawamura.

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kawamura, T. A Note on the Institution as a Nested Reasoning Structure in Terms of Bounded Cognition. Evolut Inst Econ Rev 5, 293–305 (2009). https://doi.org/10.14441/eier.5.293

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.14441/eier.5.293

Keywords

Search

Navigation