Skip to main content
SpringerLink
Log in

The characters of nonlinear vibration in the two-dimensional discrete monoatomic lattice

  • Articles
  • Published:
Chinese Science Bulletin

Abstract

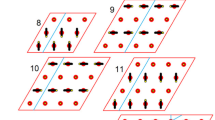
The two-dimensional discrete monoatomic lattice is analyzed. Taking nearest-neighbor interaction into account, the characters of the nonlinear vibration in two-dimensional discrete monoatomic lattice are described by the two-dimensional cubic nonlinear Schrodinger equation. Considering the quartic nonlinear potential, the two-dimensional discrete-soliton trains and the solutions perturbed by the neck mode are presented.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Tian, Q., Zhou, H., Zhu, R., A theoretical description for solitons in polyacetylene, Science in China, Ser. A, 2002, 54(7): 884–887.

    Google Scholar 

  2. Tian, Q., Wu, C. S., Solitons in superlattices: A tight-binding approach, Phys. Lett, 1999, A262: 83.

    Google Scholar 

  3. Kivshar, Y. S., Self-induced gap solitons, Phys. Rev. Lett., 1993, 70: 3055.

    Article  Google Scholar 

  4. Alfimov, G., Konotop, V.V., On the existence of gap, Physica, 2000, D146: 307.

    Google Scholar 

  5. Bang, O., Christiansen, P. L., If, F. et al., White noise in the two-dimensional nonlinear Schrodinger equation, Applicable Analysis, 1995, 57: 3–15.

    Article  Google Scholar 

  6. Ablowitz, M. J., Clarkson, P. A., Solitons, nonlinear evolution equations and inverse scattering, London Mathematical Society Note Series, 1991, 149: 17–179.

    Google Scholar 

  7. Anders, I., Asymptotics of the coupled solutions of the modified Kadomtsev-Petnashvili equation, Proceedings of Institute of Mathematics of NAS of Ukraine, 2002, 43(1): 291–295.

    Google Scholar 

  8. Zakharov, V., Shock waves propagated on solitons on the surface of a fluid, Izv. Vyszh. Vchebn. Zaved. Radiofiz, 1986, 29(9): 1073.

    Google Scholar 

  9. Anders, I., Kotlyaroy, V., Khruslov, E., Curned asymptotic solitons of the Kadomtsev Petviashvili equation, Theor. Math. Phys., 1994, 99: 402.

    Article  Google Scholar 

  10. Masayoshi Tajiri, Hiroyuki Miura, Takahito Arai, Resonant interaction of modulational instability with a periodic soliton in the Devey-Stevartson equation, Phys. Rev, 2002, E66: 067601.

    Google Scholar 

  11. Remoissenet, M., Waves Called Solitons, Berlin-Heidelberg-New York: Springer-Verlag, 1996, 138–204.

    Google Scholar 

  12. Sulem, P. L., Sulem, C., Nonlinear Schrodinger Equation: Self-focusing and Wave Collapse, New York: Springer-Verlag, 1999.

    Google Scholar 

  13. Yoshida, H., Construction of higher order symplectic integrators, Phys. Lett., 1990, A150: 262–268.

    Google Scholar 

  14. Carter, J. D., Segur, H., Instabilities in the two-dimensional cubic nonlinear Schrodinger equation, Phys. Rev., 2003, E68: 045601.

    Google Scholar 

  15. Manakov, S. V., On the theory of two-dimensional stationary self-focusing of electromagnetic manes, Sov. Phys. JETP, 1974, 38: 232–240.

    Google Scholar 

  16. Benney, D. J., Roshes, G. J., Wave instabilities, Studies in Applied Mathematics, 1969, 48: 377.

    Google Scholar 

  17. Davey, A., Stemartson, K., On three-dimensional packets of surface waves, Proc. R. Soc. London Ser., 1974, A338: 101–110.

    Article  Google Scholar 

  18. Pecseli, H. L., Solitons and weakly nonlinear waves in plasmas, IEEE Transactions on Plasma Science, 1985, 13: 53–86.

    Article  Google Scholar 

  19. Donnelly, R., Quantized Vortices in Helium IF, Cambridge: Cambridge University Press, 1991.

    Google Scholar 

  20. Gross, E. P., Hydrodynamics of a superfluid condensate, Math. Phys., 1963, 4: 195.

    Article  Google Scholar 

  21. Pitaevskii, L. P., Vortex linex in an imperfect Bose gas, Sov. Phys. JETP, 1961, 13: 451.

    Google Scholar 

  22. Zahkarov, V. E., Shabat, A. B., Exact theory of two-dimensional self-focusing and one-dimensional self-modulation of manes in nonlinear media, Sov. Phys. JETP, 1972, 34: 62–69.

    Google Scholar 

  23. Zahkarov, V. E., Shabat, A. B., On interactions between solitons in a stable medium, Sov. Phys. JETP, 1973, 37: 823–828.

    Google Scholar 

  24. Yang, Jianke, Ziad, H. M., Fundamental and vortex solitons in a two-dimensional optical lattice, Opt. Lett. 2003, 28(21): 2094–2096.

    Article  Google Scholar 

  25. Chen Zhigang, Hector, M., Eugenia, D. E. et al., Anisotropic enhancement of discrete diffraction and formation of two-dimensional discrete-soliton trains, Phys. Rew. Lett., 2004, 92(14): 143902.

    Article  Google Scholar 

  26. Zahkarov, V. E., Rubenchik, A. M., Instability of waveguides and solitons in nonlinear media, Sov. Phys. JETP, 1974, 38: 494–500.

    Google Scholar 

  27. Hennig, D., Tsironis, G. P., Wave transmission in nonlinear lattice, Phys. Rep., 1999, 307: 333–432.

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Scientific and Technological Office, Daqing Teachers College, 163712, Daqing, China

    Quan Xu

  2. Department of Physics, Beijing Normal University, 100875, Beijing, China

    Qiang Tian

Authors
  1. Quan Xu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Qiang Tian
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Quan Xu.

About this article

Cite this article

Xu, Q., Tian, Q. The characters of nonlinear vibration in the two-dimensional discrete monoatomic lattice. Chin.Sci.Bull. 50, 5–10 (2005). https://doi.org/10.1360/04ww0068

Download citation

  • Received:

  • Issue Date:

  • DOI: https://doi.org/10.1360/04ww0068

Keywords

Search

Navigation