Skip to main content
SpringerLink
Log in

Observer and observer-based H ∞ control of generalized Hamiltonian systemscontrol of generalized Hamiltonian systems

  • Published:
Science in China Series F: Information Sciences Aims and scope Submit manuscript

Abstract

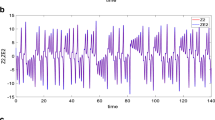
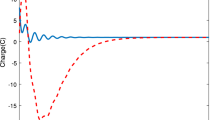
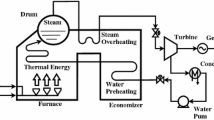
This paper deals with observer design for generalized Hamiltonian systems and its applications. First, by using the systems’ structural properties, a new observer design method called Augment Plus Feedback is provided and two kinds of observers are obtained: non-adaptive and adpative ones. Then, based on the obtained observer, H ∞ control design is investigated for generalized Hamiltonian systems, and an observer-based control design is proposed. Finally, as an application to power systems, an observer and an observer-based H ∞ control law are designed for single-machine infinite-bus systems. Simulations show that both the observer and controller obtained in this paper work very well.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Luenberger, D. G., Observers for multivariable systems, IEEE Trans. on Autom. Contr., 1966, 11: 190–197.

    Article  Google Scholar 

  2. O’Reilly, J., Observer for linear systems, New York: Academic Press, 1983.

    Google Scholar 

  3. Slotine, J. J. E., Hedrick, J. K., Misawa, E.A., On sliding observers for nonlinear systems, Journal of Dynamic Systems, Measurement and Control, 1987, 109: 245–252.

    Article  MATH  Google Scholar 

  4. Hunt, L. R., Verma, M. S., Observers for nonlinear systems in steady state, IEEE Trans. on Autom. Contr., 1994, 39(10): 2113–2118.

    Article  MATH  MathSciNet  Google Scholar 

  5. Park, J. K., Shin, D. R., Chung, T. M., Dynamic observers for linear time-invariant systems, Autimatica, 2002, 38: 1083–1087.

    Article  MATH  MathSciNet  Google Scholar 

  6. Giua, A., Seatzu, C., Basile, F., Observer-based state-feedback control of timed petri nets with deadlock recovery, IEEE Trans. on Autom. Contr., 2004, 49(1): 17–29.

    Article  MathSciNet  Google Scholar 

  7. Maschke, B. M., Ortega, R., van der Schaft, A. J., Energy-based Lyapunov functions for forced Hamiltonian systems with dissipation, IEEE Transactions on Automatic Control, 2000, 45(8): 1498–1502.

    Article  MATH  Google Scholar 

  8. Ortega, R., van der Schaft, A. J., Maschke, B., et al., Interconnection and damping assignment passivity-based control of port-controlled Hamiltonian systems, Automatica, 2002, 38(4): 585–596.

    Article  MATH  MathSciNet  Google Scholar 

  9. Cheng, D., Xi, Z., Hong, Y. et al., Energy-based stabilization in power systems, in Proceedings of the 14th IFAC World Congress, Beijing, China, Vol.O, 1999, Oxford: Pergamon Press, 1999, 297–303.

    Google Scholar 

  10. Shen, T., Ortega, R., Lu, Q. et al., Adaptive L 2 disturbance attenuation of Hamiltonian systems with parameter perturbations and application to power systems, in Proceedings of the 39th IEEE Conference on Decision and Control, Sydney, Australia, Vol.5, 2000, New York: IEEE, 2000, 4939–4944.

    Google Scholar 

  11. Sun, Y., Shen, T., Ortega, R. et al., Decentralized controller design for multimachine power systems on Hamiltonian structure, in Proceedings of the 40th IEEE Conference on Decision and Control, Orlando, Florida. New York: IEEE, 2001, 3045–3050.

    Google Scholar 

  12. Xi, Z., Cheng, D., Passivity-based stabilization and H ∞ control of the Hamiltonian control systems with dissipation and its application to power systems, Int. J. of Control, 2000, 73(18): 1686–1691.

    Article  MATH  MathSciNet  Google Scholar 

  13. Wang, Y., Cheng, D., Li, C. et al., Dissipative Hamiltonian realization and energy-based L 2-disturbance attenuation control of multimachine power systems, IEEE Trans. on Autom. Contr., 2003, 48(8): 1428–1433.

    Article  MathSciNet  Google Scholar 

  14. Wang, Y., Li, C., Cheng, D., Generalized Hamiltonian realization of time-invariant nonlinear systems, Automatica, 2003, 39(8): 1437–1443

    Article  MATH  MathSciNet  Google Scholar 

  15. Wang, Y., Li, C., Cheng, D., New approaches to dissipative Hamiltonian realization of nonlinear systems, Science in China, Ser. F, 2003, 46(6): 431–444.

    Article  MathSciNet  Google Scholar 

  16. Hebert, S. R., Cruz-Hernandez, C., Synchronization of chaotic systems: A Hamiltonian approach, in Proceedings of the American Control Conference, Chicago, Illinois, June, New York: IEEE, 2000, 769–773.

    Google Scholar 

  17. Lohmiller, W., Slotine, J. J. E., Simple observers for Hamiltonian systems, in Proceedings of the American Control Conference, Albuquerque, New Mexico, June, New York: IEEE, 1997, 2748–2753.

    Google Scholar 

  18. Lu, Q., Sun, Y., Nonlinear Control of Power Systems, Beijing: Science Press, 1993.

    Google Scholar 

  19. van der Schaft, A. J., L 2-gain and Passivity Techniques in Nonlinear Control, Berlin: Springer, 1999.

    Google Scholar 

  20. Khalil, H., Nonlinear Systems, 2nd ed., New Jersey: Prentice-Hall, 1996.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Control Science and Engineering, Shandong University, 250061, Jinan, China

    Wang Yuzhen

  2. Department of Electrical and Computer Engineering, The National University of Singapore, 117576, Singapore

    Ge S. S.

  3. Institute of Systems Science, Chinese Academy of Sciences, 100080, Beijing, China

    Cheng Daizhan

Authors
  1. Wang Yuzhen
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ge S. S.
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Cheng Daizhan
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Wang Yuzhen.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Wang, Y., Ge, S.S. & Cheng, D. Observer and observer-based H ∞ control of generalized Hamiltonian systemscontrol of generalized Hamiltonian systems. Sci China Ser F 48, 211–224 (2005). https://doi.org/10.1360/03yf0601

Download citation

  • Received:

  • Issue Date:

  • DOI: https://doi.org/10.1360/03yf0601

Keywords

Search

Navigation