Skip to main content
SpringerLink
Log in

Admittance of a one-channel conductor containing a scattering region and Andreev reflection in an N-S mesoscopic system

  • Published:
Science in China Series A: Mathematics Aims and scope Submit manuscript

Abstract

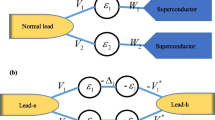
We introduce local density of states in normal-conductor-superconductor compound systems and injectivity, emissivity to describe the transmission properties in these systems. Then we study the admittance of a one-channel conductor which contains a scattering region and Andreev reflection with the discrete potential model and effective scattering approach.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Patel, N. K., Martin-Moreno, L., Pepper, M. et al., Ballistic transport in one dimension: additional quantisation produced by an electric field, J. Phys.: Condens. Matter, 1990, 2: 7247.

    Article  Google Scholar 

  2. Glazman, L. I., Khaetskii, A. V., Nonlinear quantum conductance of a lateral microconstraint in a heterostructure, Europhys. Lett., 1989, 9: 263.

    Article  Google Scholar 

  3. Kouwenhoven, L. P., van Wees, B. J., Harmans, C. J. et al., Nonlinear conductance of quantum point contacts, Phys. Rev. B, 1989, 39: 8040.

    Article  Google Scholar 

  4. Kluksdahl, N. C., Kriman, A. M., Ferry, D. K. et al., Self-consistent study of the resonant-tunneling diode, Phys. Rev. B, 1989, 39: 7720.

    Article  Google Scholar 

  5. Landauer, R., Nonlinearity in Condensed Matter, Berlin: Springer, 1987.

    Google Scholar 

  6. Büttiker, M., Thomas, H., Prêtre, A., Current partition in multiprobe conductors in the presence of slowly oscillating external potentials, Z. Phys. B, 1994, 94: 133.

    Article  Google Scholar 

  7. Prêtre, A., Thomas, H., Büttiker, M., Dynamic admittance of mesoscopic conductors: discrete-potential model, Phys. Rev. B, 1996, 54: 8130.

    Article  Google Scholar 

  8. Christen, T., Büttiker, M., Low-frequency admittance of quantized Hall conductors, Phys. Rev. B, 1996, 53:2064.

    Article  Google Scholar 

  9. Christen, T., Büttiker, M., Low frequency admittance of a quantum point contact, Phys. Rev. Lett., 1996, 77: 143.

    Article  Google Scholar 

  10. Andreev, A. F., Thermal Conductivity of The Intermediate State of Superconductors, Soviet Phys. JEPT, 1964, 19: 5.

    Google Scholar 

  11. Kastalsky, A., Observation of pair currents in superconductor-Semiconductor contacts, Phys. Rev. Lett., 1991, 67: 3026.

    Article  Google Scholar 

  12. Petrashov, V. T., Antonov, V. N., Delsing, P. et al., Phase memory effects in mesoscopic rings with superconducting “mirrors”, Phys. Rev. Lett., 1993, 70: 347.

    Article  Google Scholar 

  13. Petrashov, V. T., Antonov, V. N., Delsing, P. et al., Phase controlled conductance of mesoscopic structures with superconducting “mirrors”, Phys. Rev. Lett., 1995, 74: 5268.

    Article  Google Scholar 

  14. Hekking, F. W. J., Nazarov, Y. V., Interference of two electrons entering a superconductor, Phys. Rev. Lett., 1993, 71: 1625.

    Article  Google Scholar 

  15. Hekking, F. W. J., Nazarov, Y. V., Subgap conductivity of a superconductor-normal-metal tunnel interface, Phys. Rev. B, 1994, 49: 6847.

    Article  Google Scholar 

  16. Zaitsev, A. V., Effect of quasiparticle interference on the conductance of mesoscopic superconductor-normal-metal coupled systems, Phys. Lett., 1994, 194: 315.

    Article  Google Scholar 

  17. Guéron, S., Pothier, H., Birge, N. O et al., Superconducting proximity effect probed on a mesoscopic length scale, Phys. Rev. Lett., 1996, 77: 3025.

    Article  Google Scholar 

  18. Beenakker, C. W. J., Random-matrix theory of quantum transport, Rev. Mod. Phys., 1997, 69: 731.

    Article  Google Scholar 

  19. Lambert, C. J., Raimondi, R., Phase-coherent transport in hybrid superconducting nanostructures, J. Phys.:Condens. Matter, 1998, 10: 901.

    Article  Google Scholar 

  20. Belzig, W., Wilhelm, F. K., Bruder, C. et al. Quasiclassical Green’s function approach to mesoscopic superconductivity, Superlattices and Microstructures, 1999, 25: 1251.

    Article  Google Scholar 

  21. Gramespacher, T., Büttiker, M., Distribution functions and current-correlations in normal-metal-superconductor hetero-structures, Phys. Rev. B, 2000, 61: 8125.

    Article  Google Scholar 

  22. Martin, A. M., Gramespacher, T., Büttiker, M., Charge fluctuations in a quantum point contact attached to a superconducting lead, Phys. Rev. B, 1999, 60: R12581.

    Article  Google Scholar 

  23. Blonder, G. E., Tinkham, M., Klapwijk, T. M., Transition from metallic to tunneling regimes in superconducting microconstriction: Excess current, charge imbalance, and supercurrent conversion, Phys. Rev. B, 1982, 25: 4515.

    Article  Google Scholar 

  24. Gasparian, V., Christen, T., Büttiker, M., Partial densities of states, scattering matrices, and Green’s functions, Phys. Rev. A, 1996, 54: 4022.

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Center for Advanced Study, Tsinghua University, 100084, Beijing, China

    Zhang Gang, Zhiliang Cao & Binglin Gu

  2. Department of Physics, Tsinghua University, 100084, Beijing, China

    Zhang Gang, Wenhui Duan & Binglin Gu

Authors
  1. Zhang Gang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Zhiliang Cao
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Wenhui Duan
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Binglin Gu
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

Zhang, G., Cao, Z., Duan, W. et al. Admittance of a one-channel conductor containing a scattering region and Andreev reflection in an N-S mesoscopic system. Sci. China Ser. A-Math. 45, 1202–1210 (2002). https://doi.org/10.1360/02ys9131

Download citation

  • Received:

  • Issue Date:

  • DOI: https://doi.org/10.1360/02ys9131

Keywords

Search

Navigation