Abstract
I review the current state of determinations of the Hubble constant, which gives the length scale of the Universe by relating the expansion velocity of objects to their distance. In the last 20 years, much progress has been made and estimates now range between 60 and 75 km s−1 Mpc−1, with most now between 70 and 75 km s−1 Mpc−1, a huge improvement over the factor-of-2 uncertainty which used to prevail. Further improvements which gave a generally agreed margin of error of a few percent rather than the current 10% would be vital input to much other interesting cosmology. There are several programmes which are likely to lead us to this point in the next 10 years.
Similar content being viewed by others
1 Introduction
1.1 A brief history
The last century saw an expansion in our view of the world from a static, Galaxy-sized Universe, whose constituents were stars and “nebulae” of unknown but possibly stellar origin, to the view that the observable Universe is in a state of expansion from an initial singularity over ten billion years ago, and contains approximately 100 billion galaxies. This paradigm shift was summarised in a famous debate between Shapley and Curtis in 1920; summaries of the views of each protagonist can be found in [27] and [140].
The historical background to this change in world view has been extensively discussed and whole books have been devoted to the subject of distance measurement in astronomy [125]. At the heart of the change was the conclusive proof that what we now know as external galaxies lay at huge distances, much greater than those between objects in our own Galaxy. The earliest such distance determinations included those of the galaxies NGC 6822 [61], M33 [62] and M31 [64].
As well as determining distances, Hubble also considered redshifts of spectral lines in galaxy spectra which had previously been measured by Slipher in a series of papers [142, 143]. If a spectral line of emitted wavelength λ0 is observed at a wavelength λ, the redshift z is defined as
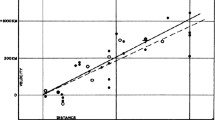
For nearby objects, the redshift corresponds to a recession velocity v which for nearby objects is given by a simple Doppler formula, v = cz. Hubble showed that a relation existed between distance and redshift (see Figure 1); more distant galaxies recede faster, an observation which can naturally be explained if the Universe as a whole is expanding. The relation between the recession velocity and distance is linear, as it must be if the same dependence is to be observed from any other galaxy as it is from our own Galaxy (see Figure 2). The proportionality constant is the Hubble constant H0, where the subscript indicates a value as measured now. Unless the Universe’s expansion does not accelerate or decelerate, the slope of the velocity-distance relation is different for observers at different epochs of the Universe.
Hubble’s original diagram of distance to nearby galaxies, derived from measurements using Cepheid variables, against velocity, derived from redshift [63]. The Hubble constant is the slope of this relation, and in this diagram is a factor of nearly 10 steeper than currently accepted values.
Illustration of the Hubble law. Galaxies at all points of the square grid are receding from the black galaxy at the centre, with velocities proportional to their distance away from it. From the point of view of the second, green, galaxy two grid points to the left, all velocities are modified by vector addition of its velocity relative to the black galaxy (red arrows). When this is done, velocities of galaxies as seen by the second galaxy are indicated by green arrows; they all appear to recede from this galaxy, again with a Hubble-law linear dependence of velocity on distance.
Recession velocities are very easy to measure; all we need is an object with an emission line and a spectrograph. Distances are very difficult. This is because in order to measure a distance, we need a standard candle (an object whose luminosity is known) or a standard ruler (an object whose length is known), and we then use apparent brightness or angular size to work out the distance. Good standard candles and standard rulers are in short supply because most such objects require that we understand their astrophysics well enough to work out what their luminosity or size actually is. Neither stars nor galaxies by themselves remotely approach the uniformity needed; even when selected by other, easily measurable properties such as colour, they range over orders of magnitude in luminosity and size for reasons that are astrophysically interesting but frustrating for distance measurement. The ideal H0 object, in fact, is one which involves as little astrophysics as possible.
Hubble originally used a class of stars known as Cepheid variables for his distance determinations. These are giant blue stars, the best known of which is αUMa, or Polaris. In most normal stars, a self-regulating mechanism exists in which any tendency for the star to expand or contract is quickly damped out. In a small range of temperature on the Hertzsprung—Russell (H-R) diagram, around 7000–8000 K, particularly at high luminosityFootnote 1, this does not happen and pulsations occur. These pulsations, the defining property of Cepheids, have a characteristic form, a steep rise followed by a gradual fall, and a period which is directly proportional to luminosity. The period-luminosity relationship was discovered by Leavitt [86] by studying a sample of Cepheid variables in the Large Magellanic Cloud (LMC). Because these stars were known to be all at the same distance, their correlation of apparent magnitude with period therefore implied the P-L relationship.
The Hubble constant was originally measured as 500 km s−1 Mpc−1 [63] and its subsequent history was a more-or-less uniform revision downwards. In the early days this was caused by biasFootnote 2 in the original samples [8], confusion between bright stars and Hii regions in the original samples [65, 131] and differences between type I and II CepheidsFootnote 3 [4]. In the second half of the last century, the subject was dominated by a lengthy dispute between investigators favouring values around 50 km s−1 Mpc−1 and those preferring higher values of 100 km s−1 Mpc−1. Most astronomers would now bet large amounts of money on the true value lying between these extremes, and this review is an attempt to explain why and also to try and evaluate the evidence for the best-guess (2007) current value. It is not an attempt to review the global history of H0 determinations, as this has been done many times, often by the original protagonists or their close collaborators. For an overall review of this process see, for example, [161] and [149]; see also data compilations and reviews by Huchra (http://cfa-www.harvard.edu/∼huchra/hubble) and Allen (http://www.institute-of-brilliant-failures.com/).
1.2 A little cosmology
The expanding Universe is a consequence, although not the only possible consequence, of general relativity coupled with the assumption that space is homogeneous (that is, it has the same average density of matter at all points at a given time) and isotropic (the same in all directions). In 1922 Friedman [47] showed that given that assumption, we can use the Einstein field equations of general relativity to write down the dynamics of the Universe using the following two equations, now known as the Friedman equations:
Here a = a(t) is the scale factor of the Universe. It is fundamentally related to redshift, because the quantity (1 + z) is the ratio of the scale of the Universe now to the scale of the Universe at the time of emission of the light (a0/a). Λ is the cosmological constant, which appears in the field equation of general relativity as an extra term. It corresponds to a universal repulsion and was originally introduced by Einstein to coerce the Universe into being static. On Hubble’s discovery of the expansion of the Universe, he removed it, only for it to reappear seventy years later as a result of new data [116, 123] (see also [21] for a review). k is a curvature term, and is −1, 0, or +1, according to whether the global geometry of the Universe is negatively curved, spatially flat, or positively curved. ρ is the density of the contents of the Universe, p is the pressure and dots represent time derivatives. For any particular component of the Universe, we need to specify an equation for the relation of pressure to density to solve these equations; for most components of interest such an equation is of the form p = wρ. Component densities vary with scale factor a as the Universe expands, and hence vary with time.
At any given time, we can define a Hubble parameter
which is obviously related to the Hubble constant, because it is the ratio of an increase in scale factor to the scale factor itself. In fact, the Hubble constant H0 is just the value of H at the current time.
If Λ = 0, we can derive the kinematics of the Universe quite simply from the first Friedman equation. For a spatially flat Universe k = 0, and we therefore have
where ρc is known as the critical density. For Universes whose densities are less than this critical density, k < 0 and space is negatively curved. For such Universes it is easy to see from the first Friedman equation that we require ȧ > 0, and therefore the Universe must carry on expanding for ever. For positively curved Universes (k > 0), the right hand side is negative, and we reach a point at which ȧ = 0. At this point the expansion will stop and thereafter go into reverse, leading eventually to a Big Crunch as ȧ becomes larger and more negative.
For the global history of the Universe in models with a cosmological constant, however, we need to consider the Λ term as providing an effective acceleration. If the cosmological constant is positive, the Universe is almost bound to expand forever, unless the matter density is very much greater than the energy density in cosmological constant and can collapse the Universe before the acceleration takes over. (A negative cosmological constant will always cause recollapse, but is not part of any currently likely world model). [21] provides further discussion of this point.
We can also introduce some dimensionless symbols for energy densities in the cosmological constant at the current time, \({\Omega _\Lambda} \equiv \Lambda/(3H_0^2)\), and in “curvature energy”, \({\Omega _k} \equiv k{c^2}/H_0^2\). By rearranging the first Friedman equation we obtain
The density in a particular component of the Universe X, as a fraction of critical density, can be written as
where the exponent α represents the dilution of the component as the Universe expands. It is related to the w parameter defined earlier by the equation α = −3(1 + w); Equation (7) holds provided that w is constant. For ordinary matter α = −3, and for radiation α = −4, because in addition to geometrical dilution the energy of radiation decreases as the wavelength increases, in addition to dilution due to the universal expansion. The cosmological constant energy density remains the same no matter how the size of the Universe increases, hence for a cosmological constant we have α = 0 and w = −1. w = −1 is not the only possibility for producing acceleration, however; any general class of “quintessence” models for which \(w < - {1 \over 3}\) will do. Moreover, there is no reason why w has to be constant with redshift, and future observations may be able to constrain models of the form w = w0 + w1z. The term “dark energy” is usually used as a general description of all such models, including the cosmological constant; in most current models, the dark energy will become increasingly dominant in the dynamics of the Universe as it expands.
In the simple case,
by definition, because Ωk = 0 implies a flat Universe in which the total energy density in matter together with the cosmological constant is equal to the critical density. Universes for which Ωk is almost zero tend to evolve away from this point, so the observed near-flatness is a puzzle known as the “flatness problem”; the hypothesis of a period of rapid expansion known as inflation in the early history of the Universe predicts this near-flatness naturally.
We finally obtain an equation for the variation of the Hubble parameter with time in terms of the Hubble constant (see e.g. [114]),
where Ωr represents the energy density in radiation and Ωm the energy density in matter.
We can define a number of distances in cosmology. The most important for present purposes are the angular diameter distance DA, which relates the apparent angular size of an object to its proper size, and the luminosity distance DL = (1 + z)2DA, which relates the observed flux of an object to its intrinsic luminosity. For currently popular models, the angular diameter distance increases to a maximum as z increases to a value of order 1, and decreases thereafter. Formulae for, and fuller explanations of, both distances are given by [56].
2 Local Methods and Cepheid Variables
2.1 Preliminary remarks
As we have seen, in principle a single object whose spectrum reveals its recession velocity, and whose distance or luminosity is accurately known, gives a measurement of the Hubble constant. In practice, the object must be far enough away for the dominant contribution to the motion to be the velocity associated with the general expansion of the Universe (the “Hubble flow”), as this expansion velocity increases linearly with distance whereas other nuisance velocities, arising from gravitational interaction with nearby matter, do not. For nearby galaxies, motions associated with the potential of the local environment are about 200–300 km s−1, requiring us to measure distances corresponding to recession velocities of a few thousand km s−1 or greater. These recession velocities correspond to distances of at least a few tens of Mpc.
For large distances, corresponding to redshifts approaching 1, the relation between spectroscopically measured redshift and luminosity (or angular diameter) distance is no longer linear and depends on the matter density Ωm and dark energy density Ωλ, as well as the Hubble constant. This is less of a problem, because as we shall see in Section 3, these parameters are probably at least as well determined as the Hubble constant itself.
Unfortunately, there is no object, or class of object, whose luminosity can be determined unambiguously in a single step and which can also be observed at distances of tens of Mpc. The approach, used since the original papers by Hubble, has therefore been to measure distances of nearby objects and use this knowledge to calibrate the brightness of more distant objects compared to the nearby ones. This process must be repeated several times in order to bootstrap one’s way out to tens of Mpc, and has been the subject of many reviews and books (see e.g. [125]). The process has a long and tortuous history, with many controversies and false turnings, and which as a by-product included the discovery of a large amount of stellar astrophysics. The astrophysical content of the method is a disadvantage, because errors in our understanding propagate directly into errors in the distance scale and consequently the Hubble constant. The number of steps involved is also a disadvantage, as it allows opportunities for both random and systematic errors to creep into the measurement. It is probably fair to say that some of these errors are still not universally agreed on. The range of recent estimates is from 60 to 75 km s−1 Mpc−1, and the reasons for the disagreements (in many cases by different analysis of essentially the same data) are often quite complex.
2.2 Basic principle
We first outline the method briefly, before discussing each stage in more detail. Nearby stars have a reliable distance measurement in the form of the parallax effect. This effect arises because the earth’s motion around the sun produces an apparent shift in the position of nearby stars compared to background stars at much greater distances. The shift has a period of a year, and an angular amplitude on the sky of the Earth-Sun distance divided by the distance to the star. The definition of the parsec is the distance which gives a parallax of one arcsecond, and is equivalent to 3.26 light-years, or 3.09 × 1016 m. The field of parallax measurement was revolutionised by the Hipparcos satellite, which measured thousands of stellar parallax distances, including observations of 223 Galactic Cepheids; of the Cepheids, 26 yielded determinations of reasonable significance [41].
Some relatively nearby stars exist in clusters of a few hundred stars known as “open clusters”. These stars can be plotted on a Hertzsprung—Russell diagram of temperature, deduced from their colour together with Wien’s law, against apparent luminosity. Such plots reveal a characteristic sequence, known as the “main sequence” which ranges from red, faint stars to blue, bright stars. This sequence corresponds to the main phase of stellar evolution which stars occupy for most of their lives when they are stably burning hydrogen. In some nearby clusters, notably the Hyades, we have stars all at the same distance and for which parallax effects can give the absolute distance. In such cases, the main sequence can be calibrated so that we can predict the absolute luminosity of a main-sequence star of a given colour. Applying this to other clusters, a process known as “main sequence fitting”, can also give the absolute distance to these other clusters.
The next stage of the bootstrap process is to determine the distance to the nearest objects outside our own Galaxy, the Large and Small Magellanic Clouds. For this we can apply the open-cluster method directly, by observing open clusters in the LMC. Alternatively, we can use calibrators whose true luminosity we know, or can predict from their other properties. Such calibrators must be present in the LMC and also in open clusters (or must be close enough for their parallaxes to be directly measurable).
These calibrators include Mira variables, RR Lyrae stars and Cepheid variable stars, of which Cepheids are intrinsically the most luminous. All of these have variability periods which are correlated with their absolute luminosity, and in principle the measurement of the distance of a nearby object of any of these types can then be used to determine distances to more distant similar objects simply by observing and comparing the variability periods.
The LMC lies at about 50 kpc, about three orders of magnitude less than that of the distant galaxies of interest for the Hubble constant. However, one class of variable stars, Cepheid variables, can be seen in both the LMC and in galaxies at much greater distances. The coming of the Hubble Space Telescope has been vital for this process, as only with the HST can Cepheids be reliably identified and measured in such galaxies. It is impossible to overstate the importance of Cepheids; without them, the connection between the LMC and external galaxies is very hard to make.
Even the HST galaxies containing Cepheids are not sufficient to allow the measurement of the universal expansion, because they are not distant enough for the dominant velocity to be the Hubble flow. The final stage is to use galaxies with distances measured with Cepheid variables to calibrate other indicators which can be measured to cosmologically interesting distances. The most promising indicator consists of type Ia supernovae (SNe), which are produced by binary systems in which a giant star is dumping mass on to a white dwarf which has already gone through its evolutionary process and collapsed to an electron-degenerate remnant; at a critical point, the rate and amount of mass dumping is sufficient to trigger a supernova explosion. The physics of the explosion, and hence the observed light-curve of the rise and slow fall, has the same characteristic regardless of distance. Although the absolute luminosity of the explosion is not constant, type Ia supernovae have similar light-curves [119, 5, 148] and in particular there is a very good correlation between the peak brightness and the degree of fading of the supernova 15 daysFootnote 4 after peak brightness (a quantity known as Δm15 [118, 53]). If SNe Ia can be detected in galaxies with known Cepheid distances, this correlation can be calibrated and used to determine distances to any other galaxy in which a SN Ia is detected. Because of the brightness of supernovae, they can be observed at large distances and hence, finally, a comparison between redshift and distance will give a value of the Hubble constant.
There are alternative indicators which can be used instead of SNe Ia for determination of H0; all of them rely on the correlation of some easily observable property of galaxies with their luminosity. For example, the edge-on rotation velocity v of spiral galaxies scales with luminosity as L ∝ v4, a scaling known as the Tully—Fisher relation [162]. There is an equivalent for elliptical galaxies, known as the Faber—Jackson relation [36]. In practice, more complex combinations of observed properties are often used such as the Dn parameter of [34] and [91], to generate measurable properties of elliptical galaxies which correlate well with luminosity, or the “fundamental plane” [34, 32] between three properties, the luminosity within an effective radiusFootnote 5, the effective radius, and the central stellar velocity dispersion. Here again, the last two parameters are measurable. Finally, the degree to which stars within galaxies are resolved depends on distance, in the sense that closer galaxies have more statistical “bumpiness” in the surface-brightness distribution [157]. This method of surface brightness fluctuation can again be calibrated by Cepheid variables in the nearer galaxies.
2.3 Problems and comments
2.3.1 Distance to the LMC
The LMC distance is probably the best-known, and least controversial, part of the distance ladder. Some methods of determination are summarised in [40] and little has changed since then. Independent calibrations using RR Lyrae variables, Cepheids and open clusters, are consistent with a distance of ∼ 50 kpc. While all individual methods have possible systematics (see in particular the next Section 2.3.2 in the case of Cepheids), their agreement within the errors leaves little doubt that the measurement is correct. Moreover, an independent measurement was made in [108] using the type II supernova 1987A in the LMC. This supernova produced an expanding ring whose angular diameter could be measured using the HST. An absolute size for the ring could also be deduced by monitoring ultraviolet emission lines in the ring and using light travel time arguments, and the distance of 51.2 ± 3.1 kpc followed from comparison of the two. An extension to this light-echo method was proposed in [144] which exploits the fact that the maximum in polarization in scattered light is obtained when the scattering angle is 90°. Hence, if a supernova light echo were observed in polarized light, its distance would be unambiguously calculated by comparing the light-echo time and the angular radius of the polarized ring.
The distance to the LMC adopted by most researchers in the field is between μ0 = 18.50 and 18.54, in the units of “distance modulus” (defined as 5 log d − 5, where d is the distance in parsecs) corresponding to a distance of 50–51 kpc. The likely error in H0 of ∼ 2% is well below the level of systematic errors in other parts of the distance ladder; recent developments in the use of standard-candle stars, main sequence fitting and the details of SN 1987A are reviewed in [2] where it is concluded that μ0 = 18.50 ± 0.02.
2.3.2 Cepheids
If the Cepheid period-luminosity relation were perfectly linear and perfectly universal (that is, if we could be sure that it applied in all galaxies and all environments) the problem of transferring the LMC distance outwards to external galaxies would be simple. Unfortunately, to very high accuracy it may be neither. Although there are other systematic difficulties in the distance ladder determinations, problems involving the physics and phenomenology of Cepheids are currently the most controversial part of the error budget, and are the primary source of differences in the derived values of H0.
The largest samples of Cepheids outside our own Galaxy come from microlensing surveys of the LMC, reported in [164]. Sandage et al. [133] reanalyse those data for LMC Cepheids and claim that the best fit involves a break in the P-L relation at P ≃ 10 days. In all three HST colours (B, V, I) the resulting slopes are different from the Galactic slopes, in the sense that at long periods, Galactic Cepheids are brighter than LMC Cepheids and are fainter at short periods. The period at which LMC and Galactic Cepheids have equal luminosities is approximately 30 days in B, but is a little more than 10 days in IFootnote 6. Sandage et al. [133] therefore claim a colour-dependent difference in the P-L relation which points to an underlying physical explanation. The problem is potentially serious in that the difference between Galactic and LMC Cepheid brightness can reach 0.3 magnitudes, corresponding to a 15% difference in inferred distance.
At least part of this difference is almost certainly due to metallicity effectsFootnote 7. Groenewegen et al. [51] assemble earlier spectroscopic estimates of metallicity in Cepheids both from the Galaxy and the LMC and compare them with their independently derived distances, obtaining a marginally significant (−0.8 ± 0.3 mag dex−1) correlation of brightness with increasing metallicity by using only Galactic Cepheids. Using also the LMC cepheids gives −0.27 ± 0.08 mag dex−1.
In some cases, independent distances to galaxies are available in the form of studies of the tip of the red giant branch. This phenomenon refers to the fact that metal-poor, population II red giant stars have a well-defined cutoff in luminosity which, in the I-band, does not vary much with nuisance parameters such as stellar population age. Deep imaging can therefore provide an independent standard candle which can be compared with that of the Cepheids, and in particular with the metallicity of the Cepheids in different galaxies. The result [130] is again that metal-rich Cepheids are brighter, with a quoted slope of −0.24 ± 0.05 mag dex−1. This agrees with earlier determinations [75, 72] and is usually adopted when a global correction is applied.
The LMC is relatively metal-poor compared to the Galaxy, and the same appears to be true of its Cepheids. On average, the Galactic Cepheids tabulated in [51] are approximately of solar metallicity, whereas those of the LMC are approximately −0.6 dex less metallic, corresponding to an 8% distance error if no correction is applied in the bootstrapping of Galactic to LMC distance. Hence, a metallicity correction must be applied when using the highest quality P-L relations from the OGLE observations of LMC Cepheids to the typically more metallic Cepheids in galaxies with SNe Ia observations.
2.4 Independent local distance-scale methods
2.4.1 Masers
One exception to the rule that Cepheids are necessary for tying local and more global distance determinations is provided by the study of masers, the prototype of which is the maser system in the galaxy NGC 4258 [23]. This galaxy has a shell of masers which are oriented almost edge-on [96, 50] and apparently in Keplerian rotation. As well as allowing a measurement of the mass of the central black hole, the velocity drift (acceleration) of the maser lines from individual maser features can also be measured. This allows a measurement of absolute size of the maser shell, and hence the distance to the galaxy. This has become steadily more accurate since the original work [54, 66, 3]. Macri et al. [92] also measure Cepheids in this object to determine a Cepheid distance (see Figure 3) and obtain consistency with the maser distance provided that the LMC distance, to which the Cepheid scale is calibrated, is 48 ± 2 kpc.
Positions of Cepheid variables in HST/ACS observations of the galaxy NGC 4258, reproduced from [92] (upper panel). Typical Cepheid lightcurves are shown in the lower panel.
Further discoveries and observations of masers could in principle establish a distance ladder without heavy reliance on Cepheids. The Water Maser Cosmology Project (http://www.cfa.harvard.edu/wmcp/index.html) is conducting monitoring and high-resolution imaging of samples of extragalactic masers, with the eventual aim of a maser distance scale accurate to ∼ 3%.
2.4.2 Other methods of establishing the distance scale
Several other different methods have been proposed to bypass some of the early rungs of the distance scale and provide direct measurements of distance to relatively nearby galaxies. Many of these are reviewed in the article by Olling [105].
One of the most promising methods is the use of detached eclipsing binary stars to determine distances directly [107]. In nearby binary stars, where the components can be resolved, the determination of the angular separation, period and radial velocity amplitude immediately yields a distance estimate. In more distant eclipsing binaries in other galaxies, the angular separation cannot be measured directly. However, the light-curve shapes provide information about the orbital period, the ratio of the radius of each star to the orbital separation, and the ratio of the stars’ luminosities. Radial velocity curves can then be used to derive the stellar radii directly. If we can obtain a physical handle on the stellar surface brightness (e.g. by study of the spectral lines) then this, together with knowledge of the stellar radius and of the observed flux received from each star, gives a determination of distance. The DIRECT project [16] has used this method to derive a distance of 964 ± 54 kpc to M33, which is higher than standard distances of 800–850 kpc [46, 87]. It will be interesting to see whether this discrepancy continues after further investigation.
A somewhat related method, but involving rotations of stars around the centre of a distant galaxy, is the method of rotational parallax [117, 106, 105]. Here one observes both the proper motion corresponding to circular rotation, and the radial velocity, of stars within the galaxy. Accurate measurement of the proper motion is difficult and will require observations from future space missions.
2.5 H0: 62 or 73?
We are now ready to try to disentangle and understand the reasons why independent analyses of the same data give values which are discrepant by twice the quoted systematic errors. Probably the fairest and most up-to-date analysis is achieved by comparing the result of Riess et al. [124] from 2005 (R05) who found H0 = 73 km s−1 Mpc−1, with statistical errors of 4 km s−1 Mpc−1, and the one of Sandage et al. [134] from 2006 (S06) who found 62.3±1.3 km s−1 Mpc−1 (statistical). Both papers quote a systematic error of 5 km s−1 Mpc−1. The R05 analysis is based on four SNe Ia: 1994ae in NGC 3370, 1998aq in NGC 3982, 1990N in NGC 4639 and 1981B in NGC 4536. The S06 analysis includes eight other calibrators, but this is not an issue as S06 find H0 = 63.3 ± 1.9 km s−1 Mpc−1 from these four calibrators separately, still a 15% difference.
Inspection of Table 13 of R05 and Table 1 of S06 reveals part of the problem; the distances of the four calibrators are generally discrepant in the two analyses, with S06 having the higher value. In the best case, SN 1994ae in NGC 3370, the discrepancy is only 0.08 magFootnote 8. In the worst case (SN 1990N in NGC 4639) R05 quotes a distance modulus μ0 = 31.74, whereas the value obtained by S06 is 32.20, corresponding to a 20–25% difference in the inferred distance and hence in H0. The quoted μ0 is formed by a combination of observations at two optical bands, V and I, and is normally defined as 2.52(m − M)I − 1.52(m − M)V, although the coefficients differ slightly between different authors. The purpose of the combination is to eliminate differential effects due to reddening, which it does exactly provided that the reddening law is known. This law has one parameter, R, known as the “ratio of total to selective extinction”, and defined as the number of magnitudes of extinction at V corresponding to one magnitude of difference between B and V.
We can investigate what is going on if we go back to the original photometry. This is given in [126] and has been corrected for various effects in the WFPC2 photometry discovered since the original work of Holtzman et al. [57]Footnote 9. If we follow R05, we proceed by using the Cepheid P-L relation for the LMC given by [156]. We then apply a global metallicity correction, to account for the fact that the LMC is less metallic than NGC 4639 by about 0.6 dex [130], and we arrive at the R05 value for μ0. Alternatively, we can use the P-L relations given by S06 and derived from earlier work by Sandage et al. [133]. These authors derived relations both for the LMC and for the Galaxy. Like the P-L relations in [156], the LMC relations are based on the OGLE observations in [164], with the addition of further Cepheids at long periods, and the Galactic relations are based on earlier work on Galactic cepheids [48, 44, 7, 9, 73]. Following S06, we derive μ0 values separately for each Cepheid for the Galaxy and LMC. We then assume that the difference between the LMC and Galactic P-L relations is entirely due to metallicity, and use the measured NGC 4639 metallicity to interpolate and find the corrected μ0 value for each Cepheid. This interpolation gives us much larger metallicity corrections than in R05. We then finally average the μ0 values to recover S06’s longer distance modulus.
The major difference is not specifically in the P-L relation assumed for the LMC, because the relation in [156] used by R05 is virtually identical to the P-L relation for long-period Cepheids used by S06. The difference lies in the correction for metallicity. R05 use a global correction
from [130] (Δ[O/H] is the metallicity of the observed Cepheids minus the metallicity of the LMC), whereas S06’s correction by interpolation between LMC and Galactic P-L relations is [126]
Which is correct? Both methods are perfectly defensible given the assumptions that are made. The S06 crucially depends on the Galactic P-L relations being correct, and in addition depends on the hypothesis that the difference between Galactic and LMC P-L relations is dominated by metallicity effects (although it is actually quite hard to think of other effects that could have anything like the same systematic effect as the composition of the stars involved). The S06 Galactic relations are based on Tammann et al. [150] (TSR03) who in turn derive them from two other methods. The first is the calibration of Cepheids in open clusters to which the distance can be measured independently (see Section 2.1), as applied in [40]. The second is a compilation in [48] including earlier measurements and compilations (see e.g. [43]) of stellar angular diameters by lunar occultation and other methods. Knowing the angular diameters and temperatures of the stars, distances can be determined [171, 6] essentially from Stefan’s law. These two methods are found to agree in [150], but this agreement and the consequent steep P-L relations for Galactic Cepheids, are crucial to the S06 case. Macri et al. [92] explicitly consider this assumption using new ACS observations of Cepheids in the galaxy NGC 4258 which have a range of metallicities [179]. They find that, if they assume the P-L relations of TSR03 whose slope varies with metallicity, the resulting μ0 determined from each Cepheid individually varies with period, suggesting that the TSR03 P-L relation overcorrects at long period and hence that the P-L assumptions of R05 are more plausible. It is probably fair to say that more data is needed in this area before final judgements are made.
The R05 method relies only on the very well-determined OGLE photometry of the LMC Cepheids and not on the Galactic measurements, but does rely on a global metallicity correction which is vulnerable to period-dependent metallicity effects. This is especially true since the bright Cepheids typically observed in relatively distant galaxies which host SNe Ia are weighted towards long periods, for which S06 claim that the metallicity correction is much larger.
Although the period-dependent metallicity correction is a major effect, there are a number of other differences which affect H0 by a few percent each.
The calibration of the type Ia supernova distance scale, and hence H0, is affected by the selection of galaxies used which contain both Cepheids and historical supernovae. Riess et al. [124] make the case for the exclusion of a number of older supernovae with measurements on photographic plates. Their exclusion, leaving four calibrators with data judged to be of high quality, has the effect of shrinking the average distances, and hence raising H0, by a few percent. Freedman et al. [45] included six galaxies including SN 1937C, excluded in [124], but obtained approximately the same value for H0.
There is a selection bias in Cepheid variable studies in that faint Cepheids are harder to see. Combined with the correlation between luminosity and period, this means that only the brighter short-period Cepheids are seen, and therefore that the P-L relation in distant galaxies is made artificially shallow [132] resulting in underestimates of distances. Neglect of this bias can give differences of several percent in the answer, and detailed simulations of it have been carried out by Teerikorpi and collaborators (see e.g. [152, 111, 112, 113]). Most authors correct explicitly for this problem — for example, Freedman et al. [45] calculate the correction analytically and find a maximum bias of about 3%. Teerikorpi and Paturel suggest that a residual bias may still be present, essentially because the amplitude of variation introduces an additional scatter in brightness at a given period, in addition to the scatter in intrinsic luminosity. How big this bias is is hard to quantify, although it can in principle be eliminated by using only long-period Cepheids at the cost of increases in the random error.
Further possible effects include differences in SNe Ia luminosities as a function of environment. Wang et al. [170] used a sample of 109 supernovae to determine a possible effect of metallicity on SNe Ia luminosity, in the sense that supernovae closer to the centre of the galaxy (and hence of higher metallicity) are brighter. They include colour information using the indicator ΔC12 ≡ (B − V)12 days, the B − V colour at 12 days after maximum, as a means of reducing scatter in the relation between peak luminosity and Δm15 which forms the traditional standard candle. Their value of H0 is, however, quite close to the Key Project value, as they use the four galaxies of [124] to tie the supernova and Cepheid scales together. This closeness indicates that the SNe Ia environment dependence is probably a small effect compared with the systematics associated with Cepheid metallicity.
In summary, local distance measures have converged to within 15%, a vast improvement on the factor of 2 uncertainty which prevailed until the late 1980s. Further improvements are possible, but involve the understanding of some non-trivial systematics and in particular require general agreement on the physics of metallicity effects on Cepheid P-L relations.
3 The CMB and Cosmological Estimates of the Distance Scale
3.1 The physics of the anisotropy spectrum and its implications
The physics of stellar distance calibrators is very complicated, because it comes from the era in which the Universe has had time to evolve complicated astrophysics. A large class of alternative approaches to cosmological parameters in general involve going back to a substantially astrophysics-free zone, the epoch of recombination. Although none of these tests uniquely or directly determine H0, they provide joint information about H0 and other cosmological parameters which is improving at a very rapid rate.
In the Universe’s early history, its temperature was high enough to prohibit the formation of atoms, and the Universe was therefore ionized. Approximately 3 × 105 yr after the Big Bang, corresponding to a redshift zrec ∼ 1000, the temperature dropped enough to allow the formation of atoms, a point known as “recombination”. For photons, the consequence of recombination was that photons no longer scattered from ionized particles but were free to stream. After recombination, these primordial photons reddened with the expansion of the Universe, forming the cosmic microwave background (CMB) which we observe today as a black-body radiation background at 2.73 K.
In the early Universe, structure existed in the form of small density fluctuations (δρ/ρ ∼ 0.01) in the photon-baryon fluid. The resulting pressure gradients, together with gravitational restoring forces, drove oscillations, very similar to the acoustic oscillations commonly known as sound waves. At the same time, the Universe expanded until recombination. At this point, the structure was dominated by those oscillation frequencies which had completed a half-integral number of oscillations within the characteristic size of the Universe at recombination; this pattern became frozen into the photon field which formed the CMB once the photons and baryons decoupled. The process is reviewed in much more detail in [60].
The resulting “acoustic peaks” dominate the fluctuation spectrum (see Figure 4). Their angular scale is a function of the size of the Universe at the time of recombination, and the angular diameter distance between us and zrec. Since the angular diameter distance is a function of cosmological parameters, measurement of the positions of the acoustic peaks provides a constraint on cosmological parameters. Specifically, the more closed the spatial geometry of the Universe, the smaller the angular diameter distance for a given redshift, and the larger the characteristic scale of the acoustic peaks. The measurement of the peak position has become a strong constraint in successive observations (in particular Boomerang, reported in [30] and WMAP, reported in [146] and [145]) and corresponds to an approximately spatially flat Universe in which Ωm + ΩΛ ≃ 1.
Diagram of the CMB anisotropies, plotted as strength against spatial frequency, from the WMAP 3-year data [145]. The measured points are shown together with best-fit models to the 1-year and 3-year WMAP data. Note the acoustic peaks, the largest of which corresponds to an angular scale of about half a degree.
But the global geometry of the Universe is not the only property which can be deduced from the fluctuation spectrumFootnote 10. The peaks are also sensitive to the density of baryons, of total (baryonic plus dark) matter, and of dark energy (energy associated with the cosmological constant or more generally with \(w < - {1 \over 3}\) components). These densities scale with the square of the Hubble parameter times the corresponding dimensionless densities (see Equation (5)) and measurement of the acoustic peaks therefore provides information on the Hubble constant, degenerate with other parameters, principally the curvature energy Ωk and the index w in the dark energy equation of state. The second peak strongly constrains the baryon density, \({\Omega _{\rm{b}}}H_0^2\), and the third peak is sensitive to the total matter density in the form \({\Omega _{\rm{m}}}H_0^2\).
3.2 Degeneracies and implications for H0
If the Universe is exactly flat and the dark energy is a cosmological constant, then the debate about H0 is over. The Wilkinson Anisotropy Probe (WMAP) has so far published two sets of cosmological measurements, based on one year and three years of operation [146, 145]. From the latest data, the assumption of a spatially flat Universe requires H0 = 73 ± 3 km s−1 Mpc−1, and also determines other cosmological parameters to two and in some cases three significant figures [145]. If we do not assume the Universe to be exactly flat, then we obtain a degeneracy with H0 in the sense that every decrease of 20 km s−1 Mpc−1 increases the total density of the Universe by 0.1 in units of the closure density (see Figure 5). The WMAP data by themselves, without any further assumptions or extra data, do not supply a significant constraint on H0.
Top: The allowed range of the parameters Ωm, Ωλ, from the WMAP 3-year data, is shown as a series of points (reproduced from [145]). The diagonal line shows the locus corresponding to a flat Universe (Ωm + Ωλ = 1). An exactly flat Universe corresponds to H0 ∼ 70 km s−1 Mpc−1, but lower values are allowed provided the Universe is slightly closed. Bottom: Analysis reproduced from [154] showing the allowed range of the Hubble constant, in the form of the Hubble parameter h ≡ H0/100 km s−1 Mpc−1, and Ωm by combination of WMAP 3-year data with acoustic oscillations. A range of H0 is still allowed by these data, although the allowed region shrinks considerably if we assume that w = − 1 or Ωk = 0.
There are two other major programmes which result in constraints on combinations of H0, Ωm, Ωλ (now considered as a general density in dark energy rather than specifically a cosmological constant energy density) and w. The first is the study of type Ia supernovae, which as we have seen function as standard candles, or at least easily calibratable candles. Studies of supernovae at cosmological redshifts by two different collaborations [116, 115, 123] have shown that distant supernovae are fainter than expected if the simplest possible spatially flat model (the Einstein—de Sitter model, for which Ωm = 1, Ωλ = 0) is correct. The resulting determination of luminosity distance has given constraints in the Ωm−Ωλ plane which are more or less orthogonal to the WMAP constraints.
The second important programme is the measurement of structure at more recent epochs than the epoch of recombination. This is interesting because fluctuations prior to recombination can propagate at the relativistic (\(c/\sqrt 3\)) sound speed which predominates at that time. After recombination, the sound speed drops, effectively freezing in a characteristic length scale to the structure of matter which corresponds to the propagation length of acoustic waves by the time of recombination. This is manifested in the real Universe by an expected preferred correlation length of ∼ 100 Mpc between observed baryon structures, otherwise known as galaxies. The largest sample available for such studies comes from luminous red galaxies (LRGs) in the Sloan Digital Sky Survey [177]. The expected signal has been found [35] in the form of an increased power in the cross-correlation between galaxies at separations of about 100 Mpc. It corresponds to an effective measurement of angular diameter distance to a redshift z ∼ 0.35.
As well as supernova and acoustic oscillations, several other slightly less tightly-constraining measurements should be mentioned:
-
Lyman α forest observations. The spectra of distant quasars have deep absorption lines corresponding to absorbing matter along the line of sight. The distribution of these lines measures clustering of matter on small scales and thus carries cosmological information (see e.g. [163, 95]).
-
Clustering on small scales [153]. The matter power spectrum can be measured using large samples of galaxies, giving constraints on combinations of H0, Ωm and σ8, the normalization of matter fluctuations on 8-Mpc scales.
3.2.1 Combined constraints
Tegmark et al. [154] have considered the effect of applying the SDSS acoustic oscillation detection together with WMAP data. As usual in these investigations, the tightness of the constraints depends on what is assumed about other cosmological parameters. The maximum set of assumptions (called the “vanilla” model by Tegmark et al.) includes the assumption that the spatial geometry of the Universe is exactly flat, that the dark energy contribution results from a pure w = − 1 cosmological constant, and that tensor modes and neutrinos make neglible contributions. Unsurprisingly, this gives them a very tight constraint on H0 of 73±1.9 km s−1 Mpc−1. However, even if we now allow the Universe to be not exactly flat, the use of the detection of baryon acoustic oscillations in [35] together with the WMAP data yields a 5%-error measurement of \({H_0} = 71.6_{- 4.3}^{+ 4.7}\) km s−1 Mpc−1. This is entirely consistent with the Hubble Key Project measurement from Cepheid variables, but only just consistent with the version in [134]. The improvement comes from the extra distance measurement, which provides a second joint constraint on the variable set (H0, Ωm, Ωλ, w).
Even this value, however, makes the assumption that w = −1. If we relax this assumption as well, Tegmark et al. [154] find that the constraints broaden considerably, to the point where the 2σ bounds on H0 range lie between 61 and 84 km s−1 Mpc−1 (see Figure 5 and [154]), even if the HST Key Project results [45] are added. It has to be said that both w = −1 and Ωk = 0 are highly plausible assumptionsFootnote 11, and if only one of them is correct, H0 is known to high accuracy. To put it another way, however, an independent measurement of H0 would be extremely useful in constraining all of the other cosmological parameters provided that its errors were at the 5% level or better. In fact [59], “The single most important complement to the CMB for measuring the dark energy equation of state at z > 0.5 is a determination of the Hubble constant to better than a few percent”. Olling [105] quantifies this statement by modelling the effect of improved H0 estimates on the determination of w. He finds that, although a 10% error on H0 is not a significant contribution to the current error budget on w, but that once improved CMB measurements such as those to be provided by the Planck satellite are obtained, decreasing the errors on H0 by a factor of five to ten could have equal power to much of the (potentially more expensive, but in any case usefully confirmatory) direct measurements of w planned in the next decade. In the next Section 4 explore various ways by which this might be achieved.
It is of course possible to put in extra information, at the cost of introducing more data sets and hence more potential for systematic error. Inclusion of the supernova data, as well as Ly-α forest data [95], SDSS and 2dF galaxy clustering [155, 24] and other CMB experiments (CBI, [120]; VSA, [31]; Boomerang, [93], Acbar, [85]), together with a vanilla model, unsurprisingly gives a very tight constraint on H0 of 70.5 ± 1.3 km s−1 Mpc−1. Including non-vanilla parameters one at a time also gives extremely tight constraints on the spatial flatness (Ωk = −0.003±0.006) and w (−1.04±0.06), but the constraints are again likely to loosen if both w and Ωk are allowed to depart from vanilla values. A vast literature is quickly assembling on the consequences of shoehorning together all possible combinations of different datasets with different parameter assumptions (see e.g. [26, 1, 67, 52, 175, 139]).
4 One-Step Distance Methods
4.1 Gravitational lenses
A general review of gravitational lensing is given in [169]; here we review the theory necessary for an understanding of the use of lenses in determining the Hubble constant.
4.1.1 Basics of lensing
Light is bent by the action of a gravitational field. In the case where a galaxy lies close to the line of sight to a background quasar, the quasar’s light may travel along several different paths to the observer, resulting in more than one image.
The easiest way to visualise this is to begin with a zero-mass galaxy (which bends no light rays) acting as the lens, and considering all possible light paths from the quasar to the observer which have a bend in the lens plane. From the observer’s point of view, we can connect all paths which take the same time to reach the observer with a contour, which in this case is circular in shape. The image will form at the centre of the diagram, surrounded by circles representing increasing light travel times. This is of course an application of Fermat’s principle; images form at stationary points in the Fermat surface, in this case at the Fermat minimum. Put less technically, the light has taken a straight-line path between the source and observer.
If we now allow the galaxy to have a steadily increasing mass, we introduce an extra time delay (known as the Shapiro delay) along light paths which pass through the lens plane close to the galaxy centre. This makes a distortion in the Fermat surface. At first, its only effect is to displace the Fermat minimum away from the distortion. Eventually, however, the distortion becomes big enough to produce a maximum at the position of the galaxy, together with a saddle point on the other side of the galaxy from the minimum. By Fermat’s principle, two further images will appear at these two stationary points in the Fermat surface. This is the basic three-image lens configuration, although in practice the central image at the Fermat maximum is highly demagnified and not usually seen.
If the lens is significantly elliptical and the lines of sight are well aligned, we can produce five images, consisting of four images around a ring alternating between maxima and saddle points, and a central, highly demagnified Fermat maximum. Both four-image and two-image systems (“quads” and “doubles”) are in fact seen in practice. The major use of lens systems is for determining mass distributions in the lens galaxy, since the positions and brightnesses of the images carry information about the gravitational potential of the lens. Gravitational lensing has the advantage that its effects are independent of whether the matter is light or dark, so in principle the effects of both baryonic and non-baryonic matter can be probed.
4.1.2 Principles of time delays
Refsdal [122] pointed out that if the background source is variable, it is possible to measure an absolute distance within the system and therefore the Hubble constant. To see how this works, consider the light paths from the source to the observer corresponding to the individual lensed images. Although each is at a stationary point in the Fermat time delay surface, the absolute light travel time for each will generally be different, with one of the Fermat minima having the smallest travel time. Therefore, if the source brightens, this brightening will reach the observer at different times corresponding to the two different light paths. Measurement of the time delay corresponds to measuring the difference in the light travel times, each of which is individually given by
where α, β and θ are angles defined above in Figure 6, D1, Ds and D1s are angular diameter distances also defined in Figure 6, z1 is the lens redshift, and ψ(θ) is a term representing the Shapiro delay of light passing through a gravitational field. Fermat’s principle corresponds to the requirement that ∇τ = 0. Once the differential time delays are known, we can then calculate the ratio of angular diameter distances which appears in the above equation. If the source and lens redshifts are known, H0 follows immediately. A handy rule of thumb which can be derived from this equation for the case of a 2-image lens, if we make the assumption that the matter distribution is isothermalFootnote 12 and H0 = 70 km s−1 Mpc−1, is
where z1 is the lens redshift, s is the separation of the images (approximately twice the Einstein radius), f > 1 is the ratio of the fluxes and D is the value of DsD1/D1s in Gpc. A larger time delay implies a correspondingly lower H0.
Basic geometry of a gravitational lens system, reproduced from [169].
The first gravitational lens was discovered in 1979 [168] and monitoring programmes began soon afterwards to determine the time delay. This turned out to be a long process involving a dispute between proponents of a ∼ 400−day and a ∼ 550−day delay, and ended with a determination of 417 ± 2 days [84, 136]. Since that time, 17 more time delays have been determined (see Table 1). In the early days, many of the time delays were measured at radio wavelengths by examination of those systems in which a radio-loud quasar was the multiply imaged source (see Figure 7). Recently, optically-measured delays have dominated, due to the fact that only a small optical telescope in a site with good seeing is needed for the photometric monitoring, whereas radio time delays require large amounts of time on long-baseline interferometers which do not exist in large numbersFootnote 13.
The lens system JVAS B0218+357. On the right is shown the measurement of time delay of about 10 days from asynchronous variations of the two lensed images [10]. The left panels show the HST/ACS image [178] on which can be seen the two images and the spiral lensing galaxy, and the radio MERLIN+VLA image [11] showing the two images together with an Einstein ring.
4.1.3 The problem with lens time delays
Unlike local distance determinations (and even unlike cosmological probes which typically use more than one measurement), there is only one major systematic piece of astrophysics in the determination of H0 by lenses, but it is a very important one. This is the form of the potential in Equation (12). If one parametrises the potential in the form of a power law in projected mass density versus radius, the index is −1 for an isothermal model. This index has a pretty direct degeneracyFootnote 14 with the deduced length scale and therefore the Hubble constant; for a change of 0.1, the length scale changes by about 10%. The sense of the effect is that a steeper index, which corresponds to a more centrally concentrated mass distribution, decreases all the length scales and therefore implies a higher Hubble constant for a given time delay. The index cannot be varied at will, given that galaxies consist of dark matter potential wells into which baryons have collapsed and formed stars. The basic physics means that it is almost certain that matter cannot be more centrally condensed than the stars, and cannot be less centrally condensed than the theoretically favoured “universal” dark matter profile, known as a NFW profile [100].
Worse still, all matter along the line of sight contributes to the lensing potential in a particularly unpleasant way; if one has a uniform mass sheet in the region, it does not affect the image positions and fluxes which form the constraints on the lensing potential, but it does affect the time delay. It operates in the sense that, if a mass sheet is present which is not known about, the length scale obtained is too short and consequently the derived value of H0 is too high. This mass-sheet degeneracy [49] can only be broken by lensing observations alone for a lens system which has sources at multiple redshifts, since there are then multiple measurements of angular diameter distance which are only consistent, for a given mass sheet, with a single value of H0. Existing galaxy lenses do not contain examples of this phenomenon.
Even worse still, there is no guarantee that parametric models describe lens mass distributions to the required accuracy. In a series of papers [128, 172, 129, 127] non-parametric, pixellated models of galaxy mass distributions have been developed which do not require any parametric form, but only basic physical plausibility arguments such as monotonic outwards decrease of mass density. Not surprisingly, error bars obtained by this method are larger than for parametric methods, usually by factors of at least 2.
4.1.4 Now and onwards in time delays and modelling
Table 1 shows the currently measured time delays, with references and comments. Since the most recent review [80] an extra half-dozen have been added, and there is every reason to suppose that the sample will continue to grow at a similar rateFootnote 15.
Despite the apparently depressing picture painted in the previous Section 4.1.3 about the prospects for obtaining mass models from lenses, the measurement of H0 is improving in a number of ways.
First, some lenses have more constraints on the mass model than others. The word “more” here is somewhat subjective, but examples include JVAS B0218+357 which in addition to two images, also has VLBI substructure within each image and an Einstein ring formed from an extended background source, and CLASS B1933+503 which has three background radio sources, each multiply imaged. Something of a Murphy’s Law operates in the latter case, however, as compact triple radio sources tend to be of the class known as Compact Symmetric Objects (CSOs) which do not vary and therefore do not give time delays. Einstein rings in general give good constraints [78] although non-parametric models are capable of soaking up most of these in extra degrees of freedom [129]. In general however, no “golden” lenses with multiple constraints and no other modelling problems have been foundFootnote 16. The best models of all come from lenses from the SLACS survey, which have extended sources [14] but unfortunately the previous Murphy’s law applies here too; extended sources are not variable.
Second, it is possible to increase the reliability of individual lens mass models by gathering extra information. A major improvement is available by the use of stellar velocity dispersions [159, 158, 160, 82] measured in the lensing galaxy. As a standalone determinant of mass models in galaxies at z ∼ 0.5, typical of lens galaxies, such measurements are not very useful as they suffer from severe degeneracies with the structure of stellar orbits. However, the combination of lensing information (which gives a very accurate measurement of mass enclosed by the Einstein radius) and stellar dynamics (which gives, more or less, the mass enclosed within the effective radius of the stellar light) gives a measurement that is in principle a very direct constraint on the mass slope. The method has large error bars, in part due to residual dependencies on the shape of stellar orbits, but also because these measurements are very difficult; each galaxy requires about one night of good seeing on a 10-m telescope. It is also not certain that the mass slope between Einstein and effective radii is always a good indicator of the mass slope within the annulus between the lensed images. Nevertheless, this programme has the extremely beneficial effect of turning a systematic error in each galaxy into a smaller, more-or-less random error.
Third, we can remove problems associated with mass sheets associated with nearby groups by measuring them using detailed studies of the environments of lens galaxies. Recent studies of lens groups [38, 71, 37, 97] show that neglecting matter along the line of sight typically has an effect of 10–20%, with matter close to the redshift of the lens contributing most.
Finally, we can improve measurements in individual lenses which have measurement difficulties. For example, in the lenses 1830−211 [90] and B0218+357 [109] the lens galaxy position is not well known. In the case of B0218+357, York et al. [178] present deep HST/ACS data which allow much better astrometry. Overall, by a lot of hard work using all methods together, the systematic errors involved in the mass model in each lens individually can be reduced to a random error. We can then study lenses as an ensemble.
Early indications, using systems with isolated lens galaxies in uncomplicated environments, and fitting isothermal mass profiles, resulted in rather low values of the Hubble constant (in the high fifties [76]). In order to be consistent with H0 ∼ 70 km s−1 Mpc−1, the mass profiles had to be steepened to the point where mass followed light; although not impossible for a single galaxy this was unlikely for an ensemble of lenses. In a subsequent analysis, Dobke and King [33] did this the other way round; they took the value of H0 = 72 ± 8 km s−1 Mpc−1 in [45] and deduced that the overall mass slope index in time-delay lenses had to be 0.2–0.3 steeper than isothermal. If true, this is worrying because investigation of a large sample of SLACS lenses with well-determined mass slopes [82] reveals an average slope which is nearly isothermal.
More recent analyses, including information available since then, may be indicating that the lens galaxies in some earlier analyses may indeed, by bad luck, be unusually steep. For example, Treu and Koopmans [159] find that PG1115+080 has an unusually steep index (0.35 steeper than isothermal) yielding a > 20% underestimate of H0. The exact value of H0 from all eighteen lenses together is a rather subjective undertaking as it depends on one’s view of the systematics in each lens and the degree to which they have been reduced to random errors. My estimate on the most optimistic assumptions is 66 ± 3 km s−1 Mpc−1, although you really don’t want to know how I got thisFootnote 17.
A more sophisticated meta-analysis has recently been done in [102] using a Monte Carlo method to account for quantities such as the presence of clusters around the main lens galaxy and the variation in profile slopes. He obtains (68±6±8) km s−1 Mpc−1. It is, however, still an uncomfortable fact that the individual H0 determinations have a greater spread than would be expected on the basis of the formal errors. Meanwhile, an arguably more realistic approach [127] is to simultaneously model ten of the eighteen time-delay lenses using fully non-parametric models. This should account more or less automatically for many of the systematics associated with the possible galaxy mass models, although it does not help us with (or excuse us from further work to determine) the presence of mass sheets and their associated degeneracies. The result obtained is \(72_{- 12}^{+ 8}\) km s−1 Mpc−1. These ten lenses give generally higher H0 values from parametric models than the ensemble of 18 known lenses with time delays; the analysis of these ten according to the parametric prescriptions in Appendix A gives H0 = 68.5 rather than 66.2 km s−1 Mpc−1.
To conclude; after a slow start, lensing is beginning to make a useful contribution to determination of H0, although the believable error bars are probably similar to those of local or CMB methods about eight to ten years ago. The results may just be beginning to create a tension with other methods, in the sense that H0 values in the mid-sixties are preferred if lens galaxies are more or less isothermal (see [76] for discussion of this point). Further work is urgently needed to turn systematic errors into random ones by investigating stellar dynamics and the neighbourhoods of galaxies in lens systems, and to reduce the random errors by increasing the sample of time delay lenses. It is likely, at the current rate of progress, that < 5% determinations will be achieved within the next few years, both from work on existing lenses and from new measurements of time delays. It is also worth pointing out that lensing time delays give a secure upper limit on H0, because most of the systematic effects associated with neglect of undetected masses cause overestimates of H0; from existing studies H0 > 80 km s−1 Mpc−1 is pretty much ruled out. This systematic of course makes any overall estimates of H0 in the mid-sixties from lensing very interesting.
One potentially very clean way to break mass model degeneracies is to discover a lensed type Ia supernova [103, 104]. The reason is that, as we have seen, the intrinsic brightness of SNe Ia can be determined from their lightcurve, and it can be shown that the resulting absolute magnification of the images can then be used to bypass the effective degeneracy between the Hubble constant and the radial mass slope. Oguri et al. [104] and also Bolton and Burles [13] discuss prospects for finding such objects; future surveys with the Large Synoptic Survey Telescope (LSST) and the SNAP supernova satellite are likely to uncover significant numbers of such events. With modest investment in investigation of the fields of these objects, a < 5% determination of H0 should be possible relatively quickly.
4.2 The Sunyaev—Zel’dovich effect
The basic principle of the Sunyaev—Zel’dovich (S-Z) method [147], including its use to determine the Hubble constant [141], is reviewed in detail in [12, 20]. It is based on the physics of hot (108 K) gas in clusters, which emits X-rays by bremsstrahlung emission with a surface brightness given by the equation
(see e.g. [12]), where ne is the electron density and Λe the spectral emissivity, which depends on the electron temperature.
At the same time, the electrons of the hot gas in the cluster Compton upscatter photons from the CMB radiation. At radio frequencies below the peak of the Planck distribution, this causes a “hole” in radio emission as photons are removed from this spectral region and turned into higher-frequency photons (see Figure 8). The decrement is given by an optical-depth equation,
involving many of the same parameters and a function Ψ which depends on frequency and electron temperature. It follows that, if both bX and ΔI(x) can be measured, we have two equations for the variables ne and the integrated length l∥ through the cluster and can calculate both quantities. Finally, if we assume that the projected size \({l_ \bot}\) of the cluster on the sky is equal to l∥, we can then derive an angular diameter distance if we know the angular size of the cluster. The Hubble constant is then easy to calculate, given the redshift of the cluster.
S-Z decrement observation of Abell 697 with the Ryle telescope in contours superimposed on the ROSAT grey-scale image. Reproduced from [69].
Although in principle a clean, single-step method, in practice there are a number of possible difficulties. Firstly, the method involves two measurements, each with a list of possible errors. The X-ray determination carries a calibration uncertainty and an uncertainty due to absorption by neutral hydrogen along the line of sight. The radio observation, as well as the calibration, is subject to possible errors due to subtraction of radio sources within the cluster which are unrelated to the S-Z effect. Next, and probably most importantly, are the errors associated with the cluster modelling. In order to extract parameters such as electron temperature, we need to model the physics of the X-ray cluster. This is not as difficult as it sounds, because X-ray spectral information is usually available, and line ratio measurements give diagnostics of physical parameters. For this modelling the cluster is usually assumed to be in hydrostatic equilibrium, or a “beta-model” (a dependence of electron density with radius of the form \(n(r) = {n_0}{(1 + {r^2}/r_c^2)^{- 3\beta/2}})\) is assumed. Several recent works [137, 15] relax this assumption, instead constraining the profile of the cluster with available X-ray information, and the dependence of H0 on these details is often reassuringly small (< 10%). Finally, the cluster selection can be done carefully to avoid looking at cigar-shaped clusters along the long axis (for which l⊥ = l∥) and therefore seeing more X-rays than one would predict. This can be done by avoiding clusters close to the flux limit of X-ray flux-limited samples, Reese et al. [121] estimate an overall random error budget of 20–30% for individual clusters. As in the case of gravitational lenses, the problem then becomes the relatively trivial one of making more measurements, provided there are no unforeseen systematics.
The cluster samples of the most recent S-Z determinations (see Table 2) are not independent in that different authors often observe the same clusters. The most recent work, that in [15] is larger than the others and gives a higher H0. It is worth noting, however, that if we draw subsamples from this work and compare the results with the other S-Z work, the H0 values from the subsamples are consistent. For example, the H0 derived from the data in [15] and modelling of the five clusters also considered in [69] is actually lower than the value of 66 km s−1 Mpc−1 in [69].
It therefore seems as though S-Z determinations of the Hubble constant are beginning to converge to a value of around 70 km s−1 Mpc−1, although the errors are still large and values in the low to mid-sixties are still consistent with the data. Even more than in the case of gravitational lenses, measurements of H0 from individual clusters are occasionally discrepant by factors of nearly two in either direction, and it would probably teach us interesting astrophysics to investigate these cases further.
4.3 Gravitational waves
One topic that may merit more than a brief paragraph in a few years’ time is the study of cosmology using gravitational waves. In particular, a coalescing binary system consisting of two neutron stars produces gravitational waves, and under those circumstances the measurement of the amplitude and frequency of the waves determines the distance to the object independently of the stellar masses [138]. This was studied in more detail in [22] and extended to more massive black hole systems [58, 29]. More massive coalescing signals produce lower-frequency gravitational wave signals which can be detected with the proposed LISA space-based interferometer. The major difficulty is obtaining the redshift measurement to go with the distance estimate, since the galaxy in which the coalescence event has taken place must be identified. Given this, however, the precision of the H0 measurement is limited only by weak gravitational lensing along the line of sight, and even this is reducible by observations of multiple systems or detailed investigations of matter along the line of sight. H0 determinations to ∼ 2% should be possible in this way after the launch of the LISA satellite in 2015.
5 Conclusion
The personal preference of the author, if forced to calculate a luminosity from a flux or a distance from an angular size, is to use the value of H0 ∼ 70−73 km s−1 Mpc−1 which is fast becoming standard. No one determination is individually compelling, but the coincidence of the most plausible cosmological determinations and some local determinations, together with the slow convergence of the one-step methods of gravitational lensing and the Sunyaev—Zel’dovich effect, is beginning to constitute a consensus that it is hard to visualise being overturned. Most astronomers, if forced to buy shares in a particular value, would be likely to put money into a similar range. It is, however, possibly unwise to sell the hedge fund on a 10% lower value just yet, and it is important to continue the process of nailing the value down — if only for the added value that this gives in constraints that can then be applied to other interesting cosmological parameters. Barring major surprises, the situation should become very much clearer in the next five to ten years.
Notes
This is known in the literature as the “instability strip” and is almost, but not quite, parallel to the luminosity axis on the H-R diagram; brighter Cepheids have slightly lower temperatures. The instability strip has a finite width, which causes a small degree of dispersion in period—luminosity correlations among Cepheids.
There are numerous subtle and less-subtle biases in distance measurement; see [151] for a blow-by-blow account. The simplest bias, the “classical” Malmquist bias, arises because, in any population of objects with a distribution in intrinsic luminosity, only the brighter members of the population will be seen at large distances. The result is that the inferred average luminosity is greater than the true luminosity, biasing distance measurements towards the systematically short. The Behr bias [8] from 1951 is a distance-dependent version of the Malmquist bias, namely that at higher distances, increasingly bright galaxies will be missing from samples. This leads to an overestimate of the average brightness of the standard candle which becomes worse at higher distance.
Cepheids come in two flavours: type I and type II, corresponding to population I and II stars. Population II stars are the first generation of stars, which formed before the enrichment of the ISM by detritus from earlier stars, and Population I stars like the Sun are the later generation which contain significant amounts of elements other than hydrogen and helium. The name “Cepheid” derives from the fact that the star δ Cephei was the first to be identified (by Goodricke in 1784). Population II Cepheids are sometimes known as W Virginis stars, after their prototype, W Vir, and a W Vir star is typically a factor of 3 fainter than a classical Cepheid of the same period.
Because of the expansion of the Universe, there is a time dilation of a factor (1 + z)−1 which must be applied to timescales measured at cosmological distances before these are used for such comparisons.
The effective radius is the radius from within which half the galaxy’s light is emitted.
Nearly all Cepheids measured in galaxies containing a SN Ia have periods > 20 days, so the usual sense of the effect is that Galactic Cepheids of a given period are brighter than LMC Cepheids.
Here, as elsewhere in astronomy, the term “metals” is used to refer to any element heavier than helium. Metallicity is usually quoted as 12 + log(O/H), where O and H are the abundances of oxygen and hydrogen.
Indeed, R05 calculate the value of H0 for SN 1994ae together with SN 1998aq according to the prescription of the Sandage et al. group as at 2005, and find 69 km s−1 Mpc−1.
There are two effects here. The first is the “long versus short” effect, which causes a decrease of recorded flux of a few percent in short exposures compared to long ones. The second is the effect of radiation damage, which affected later WFPC2 observations more than earlier ones and resulted in a uniform decrease of charge transfer efficiency and observed flux. This is again an effect at the few percent level.
See http://background.uchicago.edu/∼whu/intermediate/intermediate.html for a much longer exposition and tutorial on all these areas.
Beware plausible assumptions, however; fifteen years ago Ωλ = 0 was a highly plausible assumption.
An isothermal model is one in which the projected surface mass density decreases as 1/r. An isothermal galaxy will have a flat rotation curve, as is observed in many galaxies.
Essentially all radio time delays have come from the VLA, although monitoring programmes with MERLIN have also been attempted.
As discussed extensively in [77, 80], this is not a global degeneracy, but arises because the lensed images tell you about the mass distribution in the annulus centred on the galaxy and with inner and outer radii defined by the inner and outer images. Kochanek [77] derives detailed expressions for the time delay in terms of the central underlying and controlling parameter, the surface density in this annulus [49].
The aspiring measurer of time delays is faced with a dilemma, in terms of whether to justify the proposal in terms of measuring H0, given the previously mentioned problems with mass modelling, or in terms of determining mass models by assuming H0 = 71 km s−1 Mpc−1 (or whatever).
This term, “golden lens”, was coined over ten years ago to describe the perfect time-delay lens. Since none have been found, it is probably time to abandon it and metallic derivatives thereof, perhaps in return for vanilla CMB models and their associated error ellipses, vanilla bananas.
Full details are in Appendix A.
References
Alam, U., Sahni, V., and Starobinsky, A.A., “Exploring the properties of dark energy using type-Ia supernovae and other datasets”, J. Cosmol. Astropart. Phys., 2007(02), 011, (2007). ADS: http://adsabs.harvard.edu/abs/2007JCAP...02...11A.
Alves, D.R., “A review of the distance and structure of the Large Magellanic Cloud”, New Astron. Rev., 48, 659–665, (2004).
Argon, A.L., Greenhill, L.J., Reid, M.J., Moran, J.M., and Humphreys, E.M.L., “Toward a New Geometric Distance to the Active Galaxy NGC 4258. I. VLBI Monitoring of Water Maser Emission”, Astrophys. J., 659, 1040–1062, (2007). ADS: http://adsabs.harvard.edu/abs/2007ApJ...659.1040A.
Baade, W., “The Period-Luminosity Relation of the Cepheids”, Publ. Astron. Soc. Pac., 68, 5–16, (1956). ADS: http://adsabs.harvard.edu/abs/1956PASP...68....5B.
Barbon, R., Ciatti, F., and Rosino, L., “Light curves and characteristics of recent supernovae”, Astron. Astrophys., 29, 57–67, (1973). ADS: http://adsabs.harvard.edu/abs/1973A&A....29...57B.
Barnes, T.G., and Evans, D.S., “Stellar angular diameters and visual surface brightness. I. Late spectral types”, Mon. Not. R. Astron. Soc., 174, 489–502, (1976). ADS: http://adsabs.harvard.edu/abs/1976MNRAS.174..489B.
Barnes, T.G., Jefferys, W.H., Berger, J.O., Mueller, P.J., Orr, K., and Rodriguez, R., “A Bayesian Analysis of the Cepheid Distance Scale”, Astrophys. J., 592, 539–554, (2003). ADS: http://adsabs.harvard.edu/abs/2003ApJ...592..539B.
Behr, A., “Zur Entfernungsskala der extragalaktischen Nebel”, Astron. Nachr., 279, 97, (1951). ADS: http://adsabs.harvard.edu/abs/1951AN....279...97B.
Benedict, G.F., McArthur, B.E., Fredrick, L.W., Harrison, T.E., Slesnick, C.L., Rhee, J., Patterson, R.J., Skrutskie, M.F., Franz, O.G., Wasserman, L.H., Jefferys, W.H., Nelan, E., van Altena, W., Shelus, P.J., Hemenway, P.D., Duncombe, R.L., Story, D., Whipple, A.L., and Bradley, A.J., “Astrometry with the Hubble Space Telescope: A Parallax of the Fundamental Distance Calibrator delta Cephei”, Astron. J., 124, 1695–1705, (2002). ADS: http://adsabs.harvard.edu/abs/2002AJ....124.1695B.
Biggs, A.D., Browne, I.W.A., Helbig, P., Koopmans, L.V.E., Wilkinson, P.N., and Perley, R.A., “Time delay for the gravitational lens system B0218+357”, Mon. Not. R. Astron. Soc., 304, 349–358, (1999). ADS: http://adsabs.harvard.edu/abs/1999MNRAS.304..349B.
Biggs, A.D., Browne, I.W.A., Muxlow, T.W.B., and Wilkinson, P.N., “MERLIN/VLA imaging of the gravitational lens system B0218+357”, Mon. Not. R. Astron. Soc., 322, 821–826, (2001). ADS: http://adsabs.harvard.edu/abs/2001MNRAS.322..821B.
Birkinshaw, M., “The Sunyaev—Zel’dovich effect”, Phys. Rep., 310, 97–195, (1999). ADS: http://adsabs.harvard.edu/abs/1999PhR...310...97B.
Bolton, A.S., and Burles, S., “Prospects for the Determination of H0 through Observation of Multiply Imaged Supernovae in Galaxy Cluster Fields”, Astrophys. J., 592, 17–23, (2003). ADS: http://adsabs.harvard.edu/abs/2003ApJ...592...17B.
Bolton, A.S., Burles, S., Koopmans, L.V.E., Treu, T., and Moustakas, L.A., “The Sloan Lens ACS Survey. I. A Large Spectroscopically Selected Sample of Massive Early-Type Lens Galaxies”, Astrophys. J., 638, 703–724, (2006). ADS: http://adsabs.harvard.edu/abs/2006ApJ...638..703B.
Bonamente, M., Joy, M.K., LaRoque, S.J., Carlstrom, J.E., Reese, E.D., and Dawson, K.S., “Determination of the Cosmic Distance Scale from Sunyaev—Zel—dovich Effect and Chandra X-Ray Measurements of High-Redshift Galaxy Clusters”, Astrophys. J., 647, 25–54, (2006). ADS: http://adsabs.harvard.edu/abs/2006ApJ...647...25B.
Bonanos, A.Z., Stanek, K.Z., Kudritzki, R.P., Macri, L.M., Sasselov, D.D., Kaluzny, J., Stetson, P.B., Bersier, D., Bresolin, F., Matheson, T., Mochejska, B.J., Przybilla, N., Szentgyorgyi, A.H., Tonry, J., and Torres, G., “The First DIRECT Distance Determination to a Detached Eclipsing Binary in M33”, Astrophys. J., 652, 313–322, (2006).
Burud, I., Courbin, F., Magain, P., Lidman, C., Hutsemékers, D., Kneib, J.-P., Hjorth, J., Brewer, J., Pompei, E., Germany, L., Pritchard, J., Jaunsen, A.O., Letawe, G., and Meylan, G., “An optical time-delay for the lensed BAL quasar HE 2149–2745”, Astron. Astrophys., 383, 71–81, (2002). ADS: http://adsabs.harvard.edu/abs/2002A&A...383...71B.
Burud, I., Hjorth, J., Courbin, F., Cohen, J.G., Magain, P., Jaunsen, A.O., Kaas, A.A., Faure, C., and Letawe, G., “Time delay and lens redshift for the doubly imaged BAL quasar SBS 1520+530”, Astron. Astrophys., 391, 481, (2002). ADS: http://adsabs.harvard.edu/abs/2002A&A...391..481B.
Burud, I., Hjorth, J., Jaunsen, A.O., Andersen, M.I., Korhonen, H., Clasen, J.W., Pelt, J., Pijpers, F.P., Magain, P., and Østensen, R., “An Optical Time Delay Estimate for the Double Gravitational Lens System B1600+434”, Astrophys. J., 544, 117–122, (2000). ADS: http://adsabs.harvard.edu/abs/2000ApJ...544..117B.
Carlstrom, J.E., Holder, G.P., and Reese, E.D., “Cosmology with the Sunyaev—Zel’dovich Effect”, Annu. Rev. Astron. Astrophys., 40, 643–680, (2002). ADS: http://adsabs.harvard.edu/abs/2002ARA&A..40..643C.
Carroll, S.M., “The Cosmological Constant”, Living Rev. Relativity, 4, lrr-2001-1, (2001). URL (cited on 08 May 2007): http://www.livingreviews.org/lrr-2001-1.
Chernoff, D.F., and Finn, L.S., “Gravitational radiation, inspiraling binaries, and cosmology”, Astrophys. J. Lett., 411, L5–L8, (1993). ADS: http://adsabs.harvard.edu/abs/1993ApJ...411L...5C.
Claussen, M.J., Heiligman, G.M., and Lo, K.Y., “Water-vapour maser emission from galactic nuclei”, Nature, 310, 298–300, (1984). ADS: http://adsabs.harvard.edu/abs/1984Natur.310..298C.
Cole, S., Percival, W.J., Peacock, J.A., Norberg, P., Baugh, C.M., Frenk, C.S., Baldry, I., Bland-Hawthorn, J., Bridges, T., Cannon, R., Colless, M., Collins, C., Couch, W., Cross, N.J.G., Dalton, G., Eke, V.R., De Propris, R., Driver, S.P., Efstathiou, G., Ellis, Richard S., Glazebrook, K., Jackson, C., Jenkins, A., Lahav, O., Lewis, I., Lumsden, S., Maddox, S., Madgwick, D., Peterson, B.A., Sutherland, W., and Taylor, K., “The 2dF Galaxy Redshift Survey: power-spectrum analysis of the final data set and cosmological implications”, Mon. Not. R. Astron. Soc., 362, 505–534, (2005). ADS: http://adsabs.harvard.edu/abs/2005MNRAS.362..505C.
Courbin, F., Meylan, G., Kneib, J.-P., and Lidman, C., “Cosmic Alignment toward the Radio Einstein Ring PKS 1830–211?”, Astrophys. J., 575, 95–102, (2002). ADS: http://adsabs.harvard.edu/abs/2002ApJ...575...95C.
Cunha, J.V., Marassi, L., and Lima, J.A.S., “Constraining H0 from Sunyaev—Zel’dovich effect, Galaxy Clusters X-ray data, and Baryon Oscillations”, (2006). URL (cited on 08 May 2007): http://arXiv.org/abs/astro-ph/0611934.
Curtis, H.D., “Modern Theories of the Spiral Nebulae”, J. R. Astron. Soc. Can., 14, 317–327, (1920). ADS: http://adsabs.harvard.edu/abs/1920JRASC..14..317C.
Dai, X., Chartas, G., Agol, E., Bautz, M.W., and Garmire, G.P., “Chandra Observations of QSO 2237+0305”, Astrophys. J., 589, 100–110, (2003). ADS: http://adsabs.harvard.edu/abs/2003ApJ...589..100D.
Dalal, N., Holz, D.E., Hughes, S.A., and Jain, B., “Short GRB and binary black hole standard sirens as a probe of dark energy”, Phys. Rev. D, 74, 063006, (2006). ADS: http://adsabs.harvard.edu/abs/2006PhRvD..74f3006D.
de Bernardis, P., Ade, P.A.R., Bock, J.J., Bond, J.R., Borrill, J., Boscaleri, A., Coble, K., Crill, B.P., De Gasperis, G., Farese, P.C., Ferreira, P.G., Ganga, K., Giacometti, M., Hivon, E., Hristov, V.V., Iacoangeli, A., Jaffe, A.H., Lange, A.E., Martinis, L., Masi, S., Mason, P.V., Mauskopf, P.D., Melchiorri, A., Miglio, L., Montroy, T., Netterfield, C.B., Pascale, E., Piacentini, F., Pogosyan, D., Prunet, S., Rao, S., Romeo, G., Ruhl, J.E., Scaramuzzi, F., Sforna, D., and Vittorio, N., “A flat Universe from high-resolution maps of the cosmic microwave background radiation”, Nature, 404, 955–959, (2000). ADS: http://adsabs.harvard.edu/abs/2000Natur.404..955D.
Dickinson, C., Battye, R.A., Carreira, P., Cleary, K., Davies, R.D., Davis, R.J., Genova-Santos, R., Grainge, K., Gutiérrez, C.M., Hafez, Y.A., Hobson, M.P., Jones, M.E., Kneissl, R., Lancaster, K., Lasenby, A., Leahy, J.P., Maisinger, K., Ödman, C., Pooley, G., Rajguru, N., Rebolo, R., Rubiño Martin, J.A., Saunders, R.D.E., Savage, R.S., Scaife, A., Scott, P.F., Slosar, A., Sosa Molina, P., Taylor, A.C., Titterington, D., Waldram, E., Watson, R.A., and Wilkinson, A., “High-sensitivity measurements of the cosmic microwave background power spectrum with the extended Very Small Array”, Mon. Not. R. Astron. Soc., 353, 732–746, (2004). ADS: http://adsabs.harvard.edu/abs/2004MNRAS.353..732D.
Djorgovski, S., and Davis, M., “Fundamental properties of elliptical galaxies”, Astrophys. J., 313, 59–68, (1987). ADS: http://adsabs.harvard.edu/abs/1987ApJ...313...59D.
Dobke, B.M., and King, L.J., “A simple analysis of halo density profiles using gravitational lensing time delays”, Astron. Astrophys., 460, 647–652, (2006). ADS: http://adsabs.harvard.edu/abs/2006A&A...460..647D.
Dressler, A., Lynden-Bell, D., Burstein, D., Davies, R.L., Faber, S.M., Terlevich, R., and Wegner, G., “Spectroscopy and photometry of elliptical galaxies. I — A new distance estimator”, Astrophys. J., 313, 42–58, (1987). ADS: http://adsabs.harvard.edu/abs/1987ApJ...313...42D.
Eisenstein, D.J., Zehavi, I., Hogg, D.W., Scoccimarro, R., Blanton, M.R., Nichol, R.C., Scranton, R., Seo, H.-J., Tegmark, M., Zheng, Z., Anderson, S.F., Annis, J., Bahcall, N.A., Brinkmann, J., Burles, S., Castander, F.J., Connolly, A.J., Csabai, I., Doi, M., Fukugita, M., Frieman, J.A., Glazebrook, K., Gunn, J.E., Hendry, J.S., Hennessy, G., Ivezić, Ž., Kent, S., Knapp, G.R., Lin, H., Loh, Y.-S., Lupton, R.H., Margon, B., McKay, T.A., Meiksin, A., Munn, J.A., Pope, A., Richmond, M.W., Schlegel, D.J., Schneider, D.P., Shimasaku, K., Stoughton, C., Strauss, M.A., SubbaRao, M., Szalay, A.S., Szapudi, I., Tucker, D.L., Yanny, B., and York, D.G., “Detection of the Baryon Acoustic Peak in the Large-Scale Correlation Function of SDSS Luminous Red Galaxies”, Astrophys. J., 633, 560–574, (2005). ADS: http://adsabs.harvard.edu/abs/2005ApJ...633..560E.
Faber, S.M., and Jackson, R.E., “Velocity dispersions and mass-to-light ratios for elliptical galaxies”, Astrophys. J., 204, 668–683, (1976). ADS: http://adsabs.harvard.edu/abs/1976ApJ...204..668F.
Fassnacht, C.D., Gal, R.R., Lubin, L.M., McKean, J.P., Squires, G.K., and Readhead, A.C.S., “Mass along the Line of Sight to the Gravitational Lens B1608+656: Galaxy Groups and Implications for H0”, Astrophys. J., 642, 30–38, (2006). ADS: http://adsabs.harvard.edu/abs/2006ApJ...642...30F.
Fassnacht, C.D., and Lubin, L.M., “The Gravitational Lens-Galaxy Group Connection. I. Discovery of a Group Coincident with CLASS B0712+472”, Astron. J., 123, 627–636, (2002). ADS: http://adsabs.harvard.edu/abs/2002AJ....123..627F.
Fassnacht, C.D., Xanthopoulos, E., Koopmans, L.V.E., and Rusin, D., “A Determination of H0 with the CLASS Gravitational Lens B1608+656. III. A Significant Improvement in the Precision of the Time Delay Measurements”, Astrophys. J., 581, 823–835, (2002). ADS: http://adsabs.harvard.edu/abs/2002ApJ...581..823F.
Feast, M.W., “The Distance to the Large Magellanic Cloud, A Critical Review”, in Chu, Y.-H., Suntzeff, N.B., Hesser, J.E., and Bohlender, D.A., eds., New Views of the Magellanic Clouds, Proceedings of the 190th Symposium of the IAU, held in Victoria, BC, Canada, July 12–17, 1998, vol. 190, 542–548, (Astronomical Society of the Pacific, San Francisco, U.S.A., 1999). ADS: http://adsabs.harvard.edu/abs/1999IAUS..190..542F.
Feast, M.W., and Catchpole, R.M., “The Cepheid period-luminosity zero-point from HIP-PARCOS trigonometrical parallaxes”, Mon. Not. R. Astron. Soc., 286, L1–L5, (1997). ADS: http://adsabs.harvard.edu/abs/1997MNRAS.286L...1F.
Fohlmeister, J., Kochanek, C.S., Falco, E.E., Wambsganss, J., Morgan, N., Morgan, C.W., Ofek, E.O., Maoz, D., Keeton, C.R., Barentine, J.C., Dalton, G., Dembicky, J., Ketzeback, W., McMillan, R., and Peters, C.S., “A Time Delay for the Largest Gravitationally Lensed Quasar: SDSSJ1004+4112”, (2006). URL (cited on 08 May 2007): http://arXiv.org/abs/astro-ph/0607513.
Fouqué, P., and Gieren, W.P., “An improved calibration of Cepheid visual and infrared surface brightness relations from accurate angular diameter measurements of cool giants and supergiants”, Astron. Astrophys., 320, 799–810, (1997). ADS: http://adsabs.harvard.edu/abs/1997A&A...320..799F.
Fouqué, P., Storm, J., and Gieren, W., “Calibration of the Distance Scale from Cepheids”, in Alloin, D., and Gieren, W., eds., Stellar Candles for the Extragalactic Distance Scale, vol. 635 of Lecture Notes in Physics, 21–44, (Springer, Berlin, Germany; New York, U.S.A., 2003).
Freedman, W.L., Madore, B.F., Gibson, B.K., Ferrarese, L., Kelson, D.D., Sakai, S., Mould, J.R., Kennicutt Jr, R.C., Ford, H.C., Graham, J.A., Huchra, J.P., Hughes, S.M.G., Illingworth, G.D., Macri, L.M., and Stetson, P.B., “Final Results from the Hubble Space Telescope Key Project to Measure the Hubble Constant”, Astrophys. J., 553, 47–72, (2001). ADS: http://adsabs.harvard.edu/abs/2001ApJ...553...47F.
Freedman, W.L., Wilson, C.D., and Madore, B.F., “New Cepheid distances to nearby galaxies based on BVRI CCD photometry. II — The local group galaxy M33”, Astrophys. J., 372, 455–470, (1991). ADS: http://adsabs.harvard.edu/abs/1991ApJ...372..455F.
Friedman, A.A., “Über die Krümmung des Raumes”, Z. Phys., 10, 377–386, (1922). English translation in Cosmological Constants: Papers in Modern Cosmology, eds. Bernstein, J. and Feinberg, G., (Columbia University Press, New York, 1986).
Gieren, W.P., Fouqué, P., and Gómez, M., “Cepheid Period-Radius and Period-Luminosity Relations and the Distance to the Large Magellanic Cloud”, Astrophys. J., 496, 17–30, (1998). ADS: http://adsabs.harvard.edu/abs/1998ApJ...496...17G.
Gorenstein, M.V., Shapiro, I.I., and Falco, E.E., “Degeneracies in parameter estimation in models of gravitational lens systems”, Astrophys. J., 327, 693–711, (1988). ADS: http://adsabs.harvard.edu/abs/1988ApJ...327..693G.
Greenhill, L.J., Jiang, D.R., Moran, J.M., Reid, M.J., Lo, K.Y., and Claussen, M.J., “Detection of a Subparsec Diameter Disk in the Nucleus of NGC 4258”, Astrophys. J., 440, 619–627, (1995). ADS: http://adsabs.harvard.edu/abs/1995ApJ...440..619G.
Groenewegen, M.A.T., Romaniello, M., Primas, F., and Mottini, M., “The metallicity dependence of the Cepheid PL-relation”, Astron. Astrophys., 420, 655–663, (2004). ADS: http://adsabs.harvard.edu/abs/2004A&A...420..655G.
Habib, S., Heitmann, K., Higdon, D., Nakhleh, C., and Williams, B., “Cosmic Calibration: Constraints from the Matter Power Spectrum and the Cosmic Microwave Background”, (2007). URL (cited on 08 May 2007): http://arxiv.org/abs/astro-ph/0702348.
Hamuy, M., Phillips, M.M., Suntzeff, N.B., Schommer, R.A., Maza, J., Smith, R.C., Lira, P., and Aviles, R., “The Morphology of Type Ia Supernovae Light Curves”, Astron. J., 112, 2438–2447, (1996). ADS: http://adsabs.harvard.edu/abs/1996AJ....112.2438H.
Herrnstein, J.R., Moran, J.M., Greenhill, L.J., Diamond, P.J., Inoue, M., Nakai, N., Miyoshi, M., Henkel, C., and Riess, A., “A geometric distance to the galaxy NGC4258 from orbital motions in a nuclear gas disk”, Nature, 400, 539–541, (1999). ADS: http://adsabs.harvard.edu/abs/1999Natur.400..539H.
Hjorth, J., Burud, I., Jaunsen, A.O., Schechter, P.L., Kneib, J.-P., Andersen, M.I., Korhonen, H., Clasen, J.W., Kaas, A.A., Østensen, R., Pekt, J., and Pijpers, F.P., “The Time Delay of the Quadruple Quasar RX J0911.4+0551”, Astrophys. J., 572, L11–L14, (2002). ADS: http://adsabs.harvard.edu/abs/2002ApJ...572L..11H.
Hogg, D.W., “Distance measures in cosmology”, (1999). URL (cited on 08 May 2007): http://arxiv.org/abs/astro-ph/9905116.
Holtzman, J.A., Burrows, C.J., Casertano, S., Hester, J.J., Trauger, J.T., Watson, A.M., and Worthey, G., “The Photometric Performance and Calibration of WFPC2”, Publ. Astron. Soc. Pac., 107, 1065–1093, (1995). ADS: http://adsabs.harvard.edu/abs/1995PASP..107.1065H.
Holz, D.E., and Hughes, S.A., “Using Gravitational-Wave Standard Sirens”, Astrophys. J., 62, 15, (2005).
Hu, W., “Dark Energy Probes in Light of the CMB”, in Wolff, S.C., and Lauer, T.R., eds., Observing Dark Energy, Proceedings of a meeting held in Tucson, AZ, USA, March 18 — 20, 2004, vol. 339 of ASP Conference Series, 215–234, (Astronomical Society of the Pacific, San Francisco, U.S.A., 2005).
Hu, W., and Dodelson, S., “Cosmic Microwave Background Anisotropies”, Annu. Rev. Astron. Astrophys., 40, 171–216, (2002). ADS: http://adsabs.harvard.edu/abs/2002ARA&A..40..171H.
Hubble, E.P., “NGC 6822, a remote stellar system”, Astrophys. J., 62, 409–433, (1925). ADS: http://adsabs.harvard.edu/abs/1925ApJ....62..409H.
Hubble, E.P., “A spiral nebula as a stellar system: Messier 33”, Astrophys. J., 63, 236–274, (1926). ADS: http://adsabs.harvard.edu/abs/1926ApJ....63..236H.
Hubble, E.P., “A Relation between Distance and Radial Velocity among Extra-Galactic Nebulae”, Proc. Natl. Acad. Sci. USA, 15, 168–173, (1929).
Hubble, E.P., “A spiral nebula as a stellar system, Messier 31”, Astrophys. J., 69, 103–158, (1929). ADS: http://adsabs.harvard.edu/abs/1929ApJ....69..103H.
Humason, M.L., Mayall, N.U., and Sandage, A.R., “Redshifts and magnitudes of extragalactic nebulae”, Astron. J., 61, 97–162, (1956). ADS: http://adsabs.harvard.edu/abs/1956AJ.....61...97H.
Humphreys, E.M.L., Argon, A.L., Greenhill, L.J., Moran, J.M., and Reid, M.J., “Recent Progress on a New Distance to NGC 4258”, in Romney, J.D., and Reid, M.J., eds., Future Directions in High Resolution Astronomy: The 10th Anniversary of the VLBA, Proceedings of a meeting held in Socorro, NM, USA, June 8–12, 2003, vol. 340 of ASP Conference Series, 466–470, (Astronomical Society of the Pacific, San Francisco, U.S.A., 2005).
Ichikawa, K., and Takahashi, T., “Dark energy parametrizations and the curvature of the universe”, J. Cosmol. Astropart. Phys., 2007(02), 001, (2007). ADS: http://adsabs.harvard.edu/abs/2007JCAP...02....1I.
Jakobsson, P., Hjorth, J., Burud, I., Letawe, G., Lidman, C., and Courbin, F., “An optical time delay for the double gravitational lens system FBQ 0951+2635”, Astron. Astrophys., 431, 103–109, (2005). ADS: http://adsabs.harvard.edu/abs/2005A&A...431..103J.
Jones, M.E., Edge, A.C., Grainge, K., Grainger, W.F., Kneissl, R., Pooley, G.G., Saunders, R., Miyoshi, S.J., Tsuruta, T., Yamashita, K., Tawara, Y., Furuzawa, A., Harada, A., and Hatsukade, I., “H0 from an orientation-unbiased sample of Sunyaev—Zel’dovich and X-ray clusters”, Mon. Not. R. Astron. Soc., 357, 518–526, (2005). ADS: http://adsabs.harvard.edu/abs/2005MNRAS.357..518J.
Keeton, C.R., Falco, E.E., Impey, C.D., Kochanek, C.S., Lehár, J., McLeod, B.A., Rix, H.-W., Muñoz, J.A., and Peng, C.Y., “The Host Galaxy of the Lensed Quasar Q0957+561”, Astrophys. J., 542, 74–93, (2000). ADS: http://adsabs.harvard.edu/abs/2000ApJ...542...74K.
Keeton, C.R., and Zabludoff, A.I., “The Importance of Lens Galaxy Environments”, Astrophys. J., 612, 660–678, (2004). ADS: http://adsabs.harvard.edu/abs/2004ApJ...612..660K.
Kennicutt Jr, R.C., Bresolin, F., and Garnett, D.R., “The Composition Gradient in M101 Revisited. II. Electron Temperatures and Implications for the Nebular Abundance Scale”, Astrophys. J., 591, 801–820, (2003). ADS: http://adsabs.harvard.edu/abs/2003ApJ...591..801K.
Kervella, P., Nardetto, N., Bersier, D., Mourard, D., and Coudé du Foresto, V., “Cepheid distances from infrared long-baseline interferometry. I. VINCI/VLTI observations of seven Galactic Cepheids”, Astron. Astrophys., 416, 941–953, (2004). ADS: http://adsabs.harvard.edu/abs/2004A&A...416..941K.
Kneib, J.-P., Cohen, J.G., and Hjorth, J., “RX J0911+05: A Massive Cluster Lens at z = 0.769”, Astrophys. J., 544, L35–L39, (2000). ADS: http://adsabs.harvard.edu/abs/2000ApJ...544L..35K.
Kochanek, C.S., “Rebuilding the Cepheid Distance Scale. I. A Global Analysis of Cepheid Mean Magnitudes”, Astrophys. J., 491, 13–28, (1997). ADS: http://adsabs.harvard.edu/abs/1997ApJ...491...13K.
Kochanek, C.S., “What Do Gravitational Lens Time Delays Measure?”, Astrophys. J., 578, 25–32, (2002). ADS: http://adsabs.harvard.edu/abs/2002ApJ...578...25K.
Kochanek, C.S., “Part 2: Strong Gravitational Lensing”, in Meylan, G., Jetzer, P., and North, P., eds., Gravitational Lensing: Strong, Weak and Micro, vol. 33 of Saas-Fee Advanced Courses, 91–268, (Springer, Berlin, Germany; New York, U.S.A., 2004). ADS: http://adsabs.harvard.edu/abs/2004astro.ph..7232K.
Kochanek, C.S., Keeton, C.R., and McLeod, B.A., “The Importance of Einstein Rings”, Astrophys. J., 547, 50–59, (2001). ADS: http://adsabs.harvard.edu/abs/2001ApJ...547...50K.
Kochanek, C.S., Morgan, N.D., Falco, E.E., McLeod, B.A., Winn, J.N., Dembicky, J., and Ketzeback, B., “The Time Delays of Gravitational Lens HE 0435–1223: An Early-Type Galaxy with a Rising Rotation Curve”, Astrophys. J., 640, 47–61, (2006). ADS: http://adsabs.harvard.edu/abs/2006ApJ...640...47K.
Kochanek, C.S., and Schechter, P.L., “The Hubble Constant from Gravitational Lens Time Delays”, in Freedman, W.L., ed., Measuring and Modeling the Universe, Carnegie Observatories Centennial Symposia, vol. 2 of Carnegie Observatories Astrophysics Series, 117–137, (Cambridge University Press, Cambridge, U.K.; New York, U.S.A., 2004). ADS: http://adsabs.harvard.edu/abs/2004mmu..symp..117K.
Koopmans, L.V.E., deBruyn, A.G., Xanthopoulos, E., and Fassnacht, C.D., “A time-delay determination from VLA light curves of the CLASS gravitational lens B1600+434”, Astron. Astrophys., 356, 391–402, (2000). ADS: http://adsabs.harvard.edu/abs/2000A&A...356..391K.
Koopmans, L.V.E., Treu, T., Bolton, A.S., Burles, S., and Moustakas, L.A., “The Sloan Lens ACS Survey. III. The Structure and Formation of Early-Type Galaxies and Their Evolution since z∼1”, Astrophys. J., 640, 599–615, (2006). ADS: http://adsabs.harvard.edu/abs/2006ApJ...649..599K.
Koopmans, L.V.E., Treu, T., Fassnacht, C.D., Blandford, R.D., and Surpi, G., “The Hubble Constant from the Gravitational Lens B1608+656”, Astrophys. J., 599, 70–85, (2003). ADS: http://adsabs.harvard.edu/abs/2003ApJ...599...70K.
Kundic, T., Turner, E.L., Colley, W.N., Gott III, J.R., Rhoads, J.E., Wang, Y., Bergeron, L.E., Gloria, K.A., Long, D.C., Malhotra, S., and Wambsganss, J., “A Robust Determination of the Time Delay in 0957+561A, B and a Measurement of the Global Value of Hubble’s Constant”, Astrophys. J., 482, 75–82, (1997). ADS: http://adsabs.harvard.edu/abs/1997ApJ...482...75K.
Kuo, C.L., Ade, P.A.R., Bock, J.J., Cantalupo, C., Daub, M.D., Goldstein, J., Holzapfel, W.L., Lange, A.E., Lueker, M., Newcomb, M., Peterson, J.B., Ruhl, J., Runyan, M.C., and Torbet, E., “High-Resolution Observations of the Cosmic Microwave Background Power Spectrum with ACBAR”, Astrophys. J., 600, 32–51, (2004). ADS: http://adsabs.harvard.edu/abs/2004ApJ...600...32K.
Leavitt, H.S., and Pickering, E.C., Periods of 25 Variable Stars in the Small Magellanic Cloud., Harvard College Observatory Circular, 173, (Harvard College Observatory, Cambridge, U.S.A., 1912). ADS: http://adsabs.harvard.edu/abs/1912HarCi.173....1L.
Lee, M.G., Kim, M., Sarajedini, A., Geisler, D., and Gieren, W., “Determination of the Distance to M33 Based on Single-Epoch I-Band Hubble Space Telescope Observations of Cepheids”, Astrophys. J., 565, 959–965, (2002). ADS: http://adsabs.harvard.edu/abs/2002ApJ...565..959L.
Lehár, J., Falco, E.E., Kochanek, C.S., McLeod, B.A., Muñoz, J.A., Impey, C.D., Rix, H.-W., Keeton, C.R., and Peng, C.Y., “Hubble Space Telescope Observations of 10 Two-Image Gravitational Lenses”, Astrophys. J., 536, 584–605, (2000). ADS: http://adsabs.harvard.edu/abs/2000ApJ...536..584L.
Lovell, J.E.J., Jauncey, D.L., Reynolds, J.E., Wieringa, M.H., King, E.A., Tzioumis, A.K., McCulloch, P.M., and Edwards, P.G., “The Time Delay in the Gravitational Lens PKS 1830-211”, Astrophys. J. Lett., 508, L51–L54, (1998). ADS: http://adsabs.harvard.edu/abs/1998ApJ...508L..51L.
Lovell, J.E.J., Reynolds, J.E., Jauncey, D.L., Backus, P.R., McCulloch, P.M., Sinclair, M.W., Wilson, W.E., Tzioumis, A.K., King, E.A., Gough, R.G., Ellingsen, S.P., Phillips, C.J., Preston, R.A., and Jones, D.L., “PKS 1830-211: A Possible Compound Gravitational Lens”, Astrophys. J. Lett., 472, L5–L8, (1996). ADS: http://adsabs.harvard.edu/abs/1996ApJ...472L...5L.
Lynden-Bell, D., Burstein, D., Davies, R.L., Dressler, A., and Faber, S.M., “On best distance estimators and galaxy streaming”, in van den Bergh, S., and Pritchet, C.J., eds., The Extragalactic Distance Scale, Proceedings of the ASP 100th Anniversary Symposium, held in Victoria, BC, Canada, June 29–July 1, 1988, vol. 4 of ASP Conference Series, 307–316, (Astronomical Society of the Pacific, San Francisco, U.S.A., 1988). ADS: http://adsabs.harvard.edu/abs/1988ASPC....4..307L.
Macri, L.M., Stanek, K.Z., Bersier, D., Greenhill, L.J., and Reid, M.J., “A New Cepheid Distance to the Maser-Host Galaxy NGC 4258 and Its Implications for the Hubble Constant”, Astrophys. J., 652, 1133–1149, (2006). ADS: http://adsabs.harvard.edu/abs/2006ApJ...652.1133M.
MacTavish, C.J., Ade, P.A.R., Bock, J.J., Bond, J.R., Borrill, J., Boscaleri, A., Cabella, P., Contaldi, C.R., Crill, B.P., de Bernardis, P., De Gasperis, G., de Oliveira-Costa, A., De Troia, G., di Stefano, G., Hivon, E., Jaffe, A.H., Jones, W.C., Kisner, T.S., Lange, A.E., Lewis, A.M., Masi, S., Mauskopf, P.D., Melchiorri, A., Montroy, T.E., Natoli, P., Netterfield, C.B., Pascale, E., Piacentini, F., Pogosyan, D., Polenta, G., Prunet, S., Ricciardi, S., Romeo, G., Ruhl, J.E., Santini, P., Tegmark, M., Veneziani, M., and Vittorio, N., “Cosmological Parameters from the 2003 Flight of BOOMERANG”, Astrophys. J., 647, 799–812, (2006). ADS: http://adsabs.harvard.edu/abs/2006ApJ...647..799M.
Mason, B.S., Myers, S.T., and Readhead, A.C.S., “A Measurement of H0 from the Sunyaev—Zeldovich Effect”, Astrophys. J. Lett., 555, L11–L15, (2001). ADS: http://adsabs.harvard.edu/abs/2001ApJ...555L..11M.
McDonald, P., Seljak, U., Cen, R., Shih, D., Weinberg, D.H., Burles, S., Schneider, D.P., Schlegel, D.J., Bahcall, N.A., Briggs, J.W., Brinkmann, J., Fukugita, M., Ivezić, Ž., Kent, S., and Vanden Berk, D.E., “The Linear Theory Power Spectrum from the Lyα Forest in the Sloan Digital Sky Survey”, Astrophys. J., 635, 761–783, (2005). ADS: http://adsabs.harvard.edu/abs/2005ApJ...635..761M.
Miyoshi, M., Moran, J., Herrnstein, J., Greenhill, L., Nakai, N., Diamond, P., and Inoue, M., “Evidence for a Black Hole from High Rotation Velocities in a Sub-Parsec Region of NGC4258”, Nature, 373, 127–129, (1995).
Momcheva, I., Williams, K.A., Keeton, C.R., and Zabludoff, A.I., “A Spectroscopic Study of the Environments of Gravitational Lens Galaxies”, Astrophys. J., 641, 169–189, (2006). ADS: http://adsabs.harvard.edu/abs/2006ApJ...641..169M.
Morgan, N.D., Kochanek, C.S., Falco, E.E., and Dai, X., “Time-Delays and Mass Models for the Quadruple Lens RXJ1131-1231”, 2007 AAS/AAPT Joint Meeting held in Seattle, WA, USA, January 5–10, 2007, conference paper, (2006). ADS: http://adsabs.harvard.edu/abs/2006AAS...209.2107M, AAS Poster 021.07.
Morgan, N.D., Kochanek, C.S., Pevunova, O., and Schechter, P.L., “The Lens Redshift and Galaxy Environment for HE 0435-1223”, Astron. J., 129, 2531–2541, (2005). ADS: http://adsabs.harvard.edu/abs/2005AJ....129.2531M.
Navarro, J.F., Frenk, C.S., and White, S.D.M., “The Structure of Cold Dark Matter Halos”, Astrophys. J., 462, 563–575, (1996). ADS: http://adsabs.harvard.edu/abs/1996ApJ...462..563N.
Ofek, E.O., and Maoz, D., “Time-Delay Measurement of the Lensed Quasar HE 1104-1805”, Astrophys. J., 594, 101–106, (2003). ADS: http://adsabs.harvard.edu/abs/2003ApJ...594..1010.
Oguri, M., “Gravitational Lens Time Delays: A Statistical Assessment of Lens Model Dependences and Implications for the Global Hubble Constant”, Astrophys. J., 660, 1–15, (2007). ADS: http://adsabs.harvard.edu/abs/2007ApJ...660....10.
Oguri, M., and Kawano, Y., “Gravitational lens time delays for distant supernovae: breaking the degeneracy between radial mass profiles and the Hubble constant”, Mon. Not. R. Astron. Soc., 338, L25–L29, (2003). ADS: http://adsabs.harvard.edu/abs/2003MNRAS.338L..250.
Oguri, M., Suto, Y., and Turner, E.L., “Gravitational Lensing Magnification and Time Delay Statistics for Distant Supernovae”, Astrophys. J., 583, 584–593, (2003). ADS: http://adsabs.harvard.edu/abs/2003ApJ...583..5840.
Olling, R.P., “Accurate Extra-Galactic Distances and Dark Energy: Anchoring the Distance Scale with Rotational Parallaxes”, (2006). URL (cited on 08 May 2007): http://arXiv.org/abs/astro-ph/0607607.
Olling, R.P., and Peterson, D.M., “Galaxy Distances via Rotational Parallaxes”, (2000). URL (cited on 08 May 2007): http://arXiv.org/abs/astro-ph/0005484.
Paczyński, B., “Detached Eclipsing Binaries as Primary Distance and Age Indicators”, in Livio, M., Donahue, M., and Panagia, N., eds., The Extragalactic Distance Scale, Proceedings of the ST ScI May Symposium, held in Baltimore, MD, May 7–10, 1996, Space Telescope Science Institute Symposium Series, 273–280, (Cambridge University Press, Cambridge, U.K.; New York, U.S.A., 1997).
Panagia, N., Gilmozzi, R., Macchetto, F., Adorf, H.-M., and Kirshner, R.P., “Properties of the SN 1987A circumstellar ring and the distance to the Large Magellanic Cloud”, Astrophys. J. Lett., 380, L23–L26, (1991). ADS: http://adsabs.harvard.edu/abs/1991ApJ...380L..23P.
Patnaik, A.R., Browne, I.W.A., King, L.J., Muxlow, T.W.B., Walsh, D., and Wilkinson, P.N., “0218+357: The Smallest Separation Lensed System”, in Kayser, R., Schramm, T., and Nieser, L., eds., Gravitational Lenses, Proceedings of a conference held in Hamburg, Germany, September 9 — 13, 1991, vol. 406 of Lecture Notes in Physics, 140, (Springer, Berlin, Germany; New York, U.S.A., 1992).
Patnaik, A.R., and Narasimha, D., “Determination of time delay from the gravitational lens B1422+231”, Mon. Not. R. Astron. Soc., 326, 1403–1411, (2001). ADS: http://adsabs.harvard.edu/abs/2001MNRAS.326.1403P.
Paturel, G., and Teerikorpi, P., “The extragalactic Cepheid distance bias: Numerical simulations”, Astron. Astrophys., 413, L31–L34, (2004).
Paturel, G., and Teerikorpi, P., “The extragalactic Cepheid bias: significant influence on the cosmic distance scale”, Astron. Astrophys., 443, 883–889, (2005).
Paturel, G., and Teerikorpi, P., “The extragalactic Cepheid bias: a new test using the period-luminosity-color relation”, Astron. Astrophys., 452, 423–430, (2006).
Peacock, J.A., Cosmological Physics, (Cambridge University Press, Cambridge, U.K.; New York, U.S.A., 1999).
Perlmutter, S., Aldering, G., Goldhaber, G., Knop, R.A., Nugent, P., Castro, P.G., Deustua, S., Fabbro, S., Goobar, A., Groom, D.E., Hook, I.M., Kim, A.G., Kim, M.Y., Lee, J.C., Nunes, N.J., Pain, R., Pennypacker, C.R., Quimby, R., Lidman, C., Ellis, R.S., Irwin, M., McMahon, R.G., Ruiz-Lapuente, P., Walton, N., Schaefer, B., Boyle, B.J., Filippenko, A.V., Matheson, T., Fruchter, A.S., Panagia, N., Newberg, H.J.M., and Couch, W.J. (The Supernova Cosmology Project), “Measurements of Ω and Λ from 42 High-Redshift Supernovae”, Astrophys. J., 517, 565–586, (1999). ADS: http://adsabs.harvard.edu/abs/1999ApJ...517..565P.
Perlmutter, S., Gabi, S., Goldhaber, G., Goobar, A., Groom, D.E., Hook, I.M., Kim, A.G., Kim, M.Y., Lee, J.C., Pain, R., Pennypacker, C.R., Small, I.A., Ellis, R.S., McMahon, R.G., Boyle, B.J., Bunclark, P.S., Carter, D., Irwin, M.J., Glazebrook, K., Newberg, H.J.M., Filippenko, A.V., Matheson, T., Dopita, M., and Couch, W.J. (The Supernova Cosmology Project), “Measurements of the Cosmological Parameters Omega and Lambda from the First Seven Supernovae at z ≥ 0.35”, Astrophys. J., 483, 565–581, (1997). ADS: http://adsabs.harvard.edu/abs/1997ApJ...483..565P.
Peterson, D., and Shao, M., “The Scientific Basis for the Space Interferometry Mission”, in et al., Perryman M.A.C., ed., Hipparcos, Venice’ 97, Proceedings of the ESA Symposium, Venice, Italy, May 13–16, 1997, vol. SP-402, 749–753, (ESA Publications Division, Noordwijk, Netherlands, 1997). Related online version (cited on 10 September 2007): http://www.rssd.esa.int/?project=HIPPARCOS&page=venice97. ADS: http://adsabs.harvard.edu/abs/1997hipp.conf..749P.
Phillips, M.M., “The absolute magnitudes of Type Ia supernovae”, Astrophys. J. Lett., 413, L105–L108, (1993). ADS: http://adsabs.harvard.edu/abs/1993ApJ...413L.105P.
Pskovskii, Y.P., “The Photometric Properties of Supernovae”, Sov. Astron., 11, 63–69, (1967). ADS: http://adsabs.harvard.edu/abs/1967SvA....11...63P.
Readhead, A.C.S., Mason, B.S., Contaldi, C.R., Pearson, T.J., Bond, J.R., Myers, S.T., Padin, S., Sievers, J.L., Cartwright, J.K., Shepherd, M.C., Pogosyan, D., Prunet, S., Altamirano, P., Bustos, R., Bronfman, L., Casassus, S., Holzapfel, W.L., May, J., Pen, U.-L., Torres, S., and Udomprasert, P.S., “Extended Mosaic Observations with the Cosmic Background Imager”, Astrophys. J., 609, 498–512, (2004). ADS: http://adsabs.harvard.edu/abs/2004ApJ...609..498R.
Reese, E.D., Carlstrom, J.E., Joy, M., Mohr, J.J., Grego, L., and Holzapfel, W.L., “Determining the Cosmic Distance Scale from Interferometric Measurements of the Sunyaev—Zeldovich Effect”, Astrophys. J., 581, 53–85, (2002). ADS: http://adsabs.harvard.edu/abs/2002ApJ...581...53R.
Refsdal, S., “On the possibility of determining Hubble’s parameter and the masses of galaxies from the gravitational lens effect”, Mon. Not. R. Astron. Soc., 128, 307–310, (1964). ADS: http://adsabs.harvard.edu/abs/1964MNRAS.128..307R.
Riess, A.G., Filippenko, A.V., Challis, P., Clocchiatti, A., Diercks, A., Garnavich, P.M., Gilliland, R.L., Hogan, C.J., Jha, S., Kirshner, R.P., Leibundgut, B., Phillips, M.M., Reiss, D., Schmidt, B.P., Schommer, R.A., Smith, R.C., Spyromilio, J., Stubbs, C.W., Suntzeff, N.B., and Tonry, J., “Observational Evidence from Supernovae for an Accelerating Universe and a Cosmological Constant”, Astron. J., 116, 1009–1038, (1998). ADS: http://adsabs.harvard.edu/abs/1998AJ....116.1009R.
Riess, A.G., Li, W., Stetson, P.B., Filippenko, A.V., Jha, S., Kirshner, R.P., Challis, P.M., Garnavich, P.M., and Chornock, R., “Cepheid Calibrations from the Hubble Space Telescope of the Luminosity of Two Recent Type Ia Supernovae and a Redetermination of the Hubble Constant”, Astrophys. J., 627, 579–607, (2005). ADS: http://adsabs.harvard.edu/abs/2005ApJ...627..579R.
Rowan-Robinson, M., The Cosmological Distance Ladder: Distance and Time in the Universe, (W.H. Freeman, New York, U.S.A., 1985).
Saha, A., Thim, F., Tammann, G.A., Reindl, B., and Sandage, A., “Cepheid Distances to SNe Ia Host Galaxies Based on a Revised Photometric Zero Point of the HST WFPC2 and New PL Relations and Metallicity Corrections”, Astrophys. J. Suppl. Ser., 165, 108–137, (2006). ADS: http://adsabs.harvard.edu/abs/2006ApJS..165..108S.
Saha, P., Coles, J., Macció, A.V., and Williams, L.L.R., “The Hubble Time Inferred from 10 Time Delay Lenses”, Astrophys. J. Lett., 650, L17–L20, (2006). ADS: http://adsabs.harvard.edu/abs/2006ApJ...650L..17S.
Saha, P., and Williams, L.L.R., “Non-parametric reconstruction of the galaxy lens in PG 1115+080”, Mon. Not. R. Astron. Soc., 292, 148–156, (1997). ADS: http://adsabs.harvard.edu/abs/1997MNRAS.292..148S.
Saha, P., and Williams, L.L.R., “Beware the Nonuniqueness of Einstein Rings”, Astron. J., 122, 585–590, (2001). ADS: http://adsabs.harvard.edu/abs/2001AJ....122..585S.
Sakai, S., Ferrarese, L., Kennicutt Jr, R.C., and Saha, A., “The Effect of Metallicity on Cepheid-based Distances”, Astrophys. J., 608, 42–61, (2004). ADS: http://adsabs.harvard.edu/abs/2004ApJ...608...42S.
Sandage, A., “Current Problems in the Extragalactic Distance Scale.”, Astrophys. J., 127, 513–526, (1958). ADS: http://adsabs.harvard.edu/abs/1958ApJ...127..513S.
Sandage, A., “Cepheids as distance indicators when used near their detection limit”, Publ. Astron. Soc. Pac., 100, 935–948, (1988). ADS: http://adsabs.harvard.edu/abs/1988PASP..100..935S.
Sandage, A., Tammann, G.A., and Reindl, B., “New period-luminosity and period-color relations of classical Cepheids. II. Cepheids in LMC”, Astron. Astrophys., 424, 43–71, (2004). ADS: http://adsabs.harvard.edu/abs/2004A&A...424...43S.
Sandage, A., Tammann, G.A., Saha, A., Reindl, B., Macchetto, F.D., and Panagia, N., “The Hubble Constant: A Summary of the Hubble Space Telescope Program for the Luminosity Calibration of Type Ia Supernovae by Means of Cepheids”, Astrophys. J., 653, 843–860, (2006). ADS: http://adsabs.harvard.edu/abs/2006ApJ...653..843S.
Schechter, P.L., Bailyn, C.D., Barr, R., Barvainis, R., Becker, C.M., Bernstein, G.M., Blakeslee, J.P., Bus, S.J., Dressler, A., Falco, E.E., Fesen, R.A., Fischer, P., Gebhardt, K., Harmer, D., Hewitt, J.N., Hjorth, J., Hurt, T., Jaunsen, A.O., Mateo, M., Mehlert, D., Richstone, D.O., Sparke, L.S., Thorstensen, J.R., Tonry, J.L., Wegner, G., Willmarth, D.W., and Worthey, G., “The Quadruple Gravitational Lens PG 1115+080: Time Delays and Models”, Astrophys. J. Lett., 475, L85–L88, (1997). ADS: http://adsabs.harvard.edu/abs/1997ApJ...475L..85S.
Schild, R., and Thomson, D.J., “The Q0957+561 Time Delay From Optical Data”, Astron. J., 113, 130–135, (1997). ADS: http://adsabs.harvard.edu/abs/1997AJ....113..130S.
Schmidt, R.W., Allen, S.W., and Fabian, A.C., “An improved approach to measuring H0 using X-ray and SZ observations of galaxy clusters”, Mon. Not. R. Astron. Soc., 352, 1413–1420, (2004). ADS: http://adsabs.harvard.edu/abs/2004MNRAS.352.1413S.
Schutz, B.F., “Determining the Hubble constant from gravitational wave observations”, Nature, 323, 310–311, (1986).
Serra, P., Heavens, A., and Melchiorri, A., “Bayesian Evidence for a Cosmological Constant using new High-Redshift Supernovae Data”, (2007). URL (cited on 08 May 2007): http://arXiv.org/abs/astro-ph/0701338.
Shapley, H., “On the Existence of External Galaxies”, J. R. Astron. Soc. Can., 13, 438–446, (1919). ADS: http://adsabs.harvard.edu/abs/1919JRASC..13..438S.
Silk, J., and White, S.D.M., “The determination of Q0 using X-ray and microwave observations of galaxy clusters”, Astrophys. J. Lett., 226, L103–L106, (1978). ADS: http://adsabs.harvard.edu/abs/1978ApJ...226L.103S.
Slipher, V.M., “The Radial Velocity of the Andromeda Nebula”, Popular Astron., 22, 19–21, (1914). ADS: http://adsabs.harvard.edu/abs/1914PA.....22...19S.
Slipher, V.M., “Radial velocity observations of spiral nebulae”, Observatory, 40, 304–306, (1917). ADS: http://adsabs.harvard.edu/abs/19170bs....40..304S.
Sparks, W.B., “A direct way to measure the distances of galaxies”, Astrophys. J., 433, 19–28, (1994). ADS: http://adsabs.harvard.edu/abs/1994ApJ...433...19S.
Spergel, D.N., Bean, R., Doré, O., Nolta, M.R., Bennett, C.L., Dunkley, J., Hinshaw, G., Jarosik, N., Komatsu, E., Page, L., Peiris, H.V., Verde, L., Halpern, M., Hill, R.S., Kogut, A., Limon, M., Meyer, S.S., Odegard, N., Tucker, G.S., Weiland, J.L., Wollack, E., and Wright, E.L., “Wilkinson Microwave Anisotropy Probe (WMAP) Three Year Results: Implications for Cosmology”, (2006). URL (cited on 08 May 2007): http://arXiv.org/abs/astro-ph/0603449.
Spergel, D.N., Verde, L., Peiris, H.V., Komatsu, E., Nolta, M.R., Bennett, C.L., Halpern, M., Hinshaw, G., Jarosik, N., Kogut, A., Limon, M., Meyer, S.S., Page, L., Tucker, G.S., Weiland, J.L., Wollack, E., and Wright, E.L., “First-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Determination of Cosmological Parameters”, Astrophys. J. Suppl. Ser., 148, 175–194, (2003). ADS: http://adsabs.harvard.edu/abs/2003ApJS..148..175S.
Sunyaev, R.A., and Zeldovich, Y.B., “The Observations of Relic Radiation as a Test of the Nature of X-Ray Radiation from the Clusters of Galaxies”, Comments Astrophys. Space Phys., 4, 173, (1972).
Tammann, G.A., “Supernova statistics and related problems”, in Rees, M.J., and Stoneham, R.J., eds., Supernovae: A Survey of Current Research, Proceedings of the NATO Advanced Study Institute, held at Cambridge, UK, June 29–July 10, 1981, vol. 90 of NATO Science Series C, 371–403, (Kluwer, Dordrecht, Netherlands; Boston, U.S.A., 1982).
Tammann, G.A., and Reindl, B., “Karl Schwarzschild Lecture: The Ups and Downs of the Hubble Constant”, in Röser, S., ed., The Many Facets of the Universe — Revelations by New Instruments, Herbsttagung 2005 / 79th Annual Scientific Meeting of the Astronomische Gesellschaft, Cologne, Germany, September 26–October 1, 2005, vol. 19 of Reviews in Modern Astronomy, 1–30, (Wiley-VCH, Weinheim, Germany, 2006). ADS: http://adsabs.harvard.edu/abs/2005astro.ph.12584T.
Tammann, G.A., Sandage, A., and Reindl, B., “New Period-Luminosity and Period-Color relations of classical Cepheids: I. Cepheids in the Galaxy”, Astron. Astrophys., 404, 423–448, (2003). ADS: http://adsabs.harvard.edu/abs/2003A&A...404..423T.
Teerikorpi, P., “Observational Selection Bias Affecting the Determination of the Extragalactic Distance Scale”, Annu. Rev. Astron. Astrophys., 35, 101–136, (1997).
Teerikorpi, P., and Paturel, G., “Evidence for the extragalactic Cepheid distance bias from the kinematical distance scale”, Astron. Astrophys., 381, L37–L40, (2002).
Tegmark, M., Blanton, M.R., Strauss, M.A., Hoyle, F., Schlegel, D.J., Scoccimarro, R., Vogeley, M.S., Weinberg, D.H., Zehavi, I., Berlind, A., Budavari, T., Connolly, A.J., Eisenstein, D.J., Finkbeiner, D., Frieman, J.A., Gunn, J.E., Hamilton, A.J.S., Hui, L., Jain, B., Johnston, D., Kent, S., Lin, H., Nakajima, R., Nichol, R.C., Ostriker, J.P., Pope, A., Scranton, R., Seljak, U., Sheth, R.K., Stebbins, A., Szalay, A.S., Szapudi, I., Verde, L., Xu, Y., Annis, J., Bahcall, N.A., Brinkmann, J., Burles, S., Castander, F.J., Csabai, I., Loveday, J., Doi, M., Fukugita, M., Gott, J.R.I., Hennessy, G., Hogg, D.W., Ivezić, Ž., Knapp, G.R., Lamb, D.Q., Lee, B.C., Lupton, R.H., McKay, T.A., Kunszt, P.Z., Munn, J.A., O’Connell, L., Peoples, J., Pier, J.R., Richmond, M.W., Rockosi, C.M., Schneider, D.P., Stoughton, C., Tucker, D.L., Vanden Berk, D.E., Yanny, B., and York, D.G., “The Three-Dimensional Power Spectrum of Galaxies from the Sloan Digital Sky Survey”, Astrophys. J., 606, 702–740, (2004). ADS: http://adsabs.harvard.edu/abs/2004ApJ...606..702T.
Tegmark, M., Eisenstein, D.J., Strauss, M.A., Weinberg, D.H., Blanton, M.R., Frieman, J.A., Fukugita, M., Gunn, J.E., Hamilton, A.J.S., Knapp, G.R., Nichol, R.C., Ostriker, J.P., Padmanabhan, N., Percival, W.J., Schlegel, D.J., Schneider, D.P., Scoccimarro, R., Seljak, U., Seo, H.-J., Swanson, M., Szalay, A.S., Vogeley, M.S., Yoo, J., Zehavi, I., Abazajian, K., Anderson, S.F., Annis, J., Bahcall, N.A., Bassett, B., Berlind, A., Brinkmann, J., Budavari, T., Castander, F.J., Connolly, A.J., Csabai, I., Doi, M., Finkbeiner, D.P., Gillespie, B., Glazebrook, K., Hennessy, G.S., Hogg, D.W., Ivezić, Ž., Jain, B., Johnston, D., Kent, S., Lamb, D.Q., Lee, B.C., Lin, H., Loveday, J., Lupton, R.H., Munn, J.A., Pan, K., Park, C., Peoples, J., Pier, J.R., Pope, A., Richmond, M.W., Rockosi, C.M., Scranton, R., Sheth, R.K., Stebbins, A., Stoughton, C., Szapudi, I., Tucker, D.L., Vanden Berk, D.E., Yanny, B., and York, D.G., “Cosmological constraints from the SDSS luminous red galaxies”, Phys. Rev. D, 74, 123507, (2006). ADS: http://adsabs.harvard.edu/abs/2006PhRvD..74l3507T.
Tegmark, M., Strauss, M.A., Blanton, M.R., Abazajian, K., Dodelson, S., Sandvik, H., Wang, X., Weinberg, D.H., Zehavi, I., Bahcall, N.A., Hoyle, F., Schlegel, D.J., Scoccimarro, R., Vogeley, M.S., Berlind, A., Budavari, T., Connolly, A.J., Eisenstein, D.J., Finkbeiner, D., Frieman, J.A., Gunn, J.E., Hui, L., Jain, B., Johnston, D., Kent, S., Lin, H., Nakajima, R., Nichol, R.C., Ostriker, J.P., Pope, A., Scranton, R., Seljak, U., Sheth, R.K., Stebbins, A., Szalay, A.S., Szapudi, I., Xu, Y., Annis, J., Brinkmann, J., Burles, S., Castander, F.J., Csabai, I., Loveday, J., Doi, M., Fukugita, M., Gillespie, B., Hennessy, G., Hogg, D.W., Ivezić, Ž., Knapp, G.R., Lamb, D.Q., Lee, B.C., Lupton, R.H., McKay, T.A., Kunszt, P.Z., Munn, J.A., O’Connell, L., Peoples, J., Pier, J.R., Richmond, M.W., Rockosi, C.M., Schneider, D.P., Stoughton, C., Tucker, D.L., Vanden Berk, D.E., Yanny, B., and York, D.G., “Cosmological parameters from SDSS and WMAP”, Phys. Rev. D, 69, 103501, (2004).
Thim, F., Tammann, G.A., Saha, A., Dolphin, A., Sandage, A., Tolstoy, E., and Labhardt, L., “The Cepheid Distance to NGC 5236 (M83) with the ESO Very Large Telescope”, Astrophys. J., 590, 256–270, (2003). ADS: http://adsabs.harvard.edu/abs/2003ApJ...590..256T.
Tonry, J., and Schneider, D.P., “A new technique for measuring extragalactic distances”, Astron. J., 96, 807–815, (1988). ADS: http://adsabs.harvard.edu/abs/1988AJ......96..807T.
Treu, T., and Koopmans, L.V.E., “The Internal Structure and Formation of Early-Type Galaxies: The Gravitational Lens System MG 2016+112 at z = 1.004”, Astrophys. J., 575, 87–94, (2002). ADS: http://adsabs.harvard.edu/abs/2002ApJ...575...87T.
Treu, T., and Koopmans, L.V.E., “The internal structure of the lens PG1115+080: breaking degeneracies in the value of the Hubble constant”, Mon. Not. R. Astron. Soc., 337, L6–L10, (2002). ADS: http://adsabs.harvard.edu/abs/2002MNRAS.337L...6T.
Treu, T., and Koopmans, L.V.E., “Massive Dark Matter Halos and Evolution of Early-Type Galaxies toz∼ 1”, Astrophys. J., 611, 739–760, (2004). ADS: http://adsabs.harvard.edu/abs/2004ApJ...611..739T.
Trimble, V., “H0: The Incredible Shrinking Constant, 1925–1975”, Publ. Astron. Soc. Pac., 108, 1073–1082, (1996). ADS: http://adsabs.harvard.edu/abs/1996PASP..108.1073T.
Tully, R.B., and Fisher, J.R., “A New Method of Determining Distances to Galaxies”, Astron. Astrophys., 54, 661–673, (1977). ADS: http://adsabs.harvard.edu/abs/1977A&A....54..661T.
Tytler, D., Kirkman, D., O’Meara, J.M., Suzuki, N., Orin, A., Lubin, D., Paschos, P., Jena, T., Lin, W.-C., and Norman, M.L. Meiksin, A., “Cosmological Parameters σ8, the Baryon Density Ωb, the Vacuum Energy Density Ωλ, the Hubble Constant and the UV Background Intensity from a Calibrated Measurement of H I Lyα Absorption at z = 1.9”, Astrophys. J., 617, 1–28, (2004). ADS: http://adsabs.harvard.edu/abs/2004ApJ...617....1T.
Udalski, A., Soszynski, I., Szymanski, M., Kubiak, M., Pietrzynski, G., Wozniak, P., and Zebrun, K., “The Optical Gravitational Lensing Experiment. Cepheids in the Magellanic Clouds. IV. Catalog of Cepheids from the Large Magellanic Cloud”, Acta Astron., 49, 223–317, (1999). ADS: http://adsabs.harvard.edu/abs/1999AcA....49..223U.
Udomprasert, P.S., Mason, B.S., Readhead, A.C.S., and Pearson, T.J., “An Unbiased Measurement of H0 through Cosmic Background Imager Observations of the Sunyaev—Zel’dovich Effect in Nearby Galaxy Clusters”, Astrophys. J., 615, 63–81, (2004). ADS: http://adsabs.harvard.edu/abs/2004ApJ...615...63U.
Ullán, A., Goicoechea, L.J., Zheleznyak, A.P., Koptelova, E., Bruevich, V.V., Akhunov, T., and Burkhonov, O., “Time delay of SBS 0909+532”, Astron. Astrophys., 452, 25–35, (2006). ADS: http://adsabs.harvard.edu/abs/2006A&A...452...25U.
Vuissoz, C., Courbin, F., Sluse, D., Meylan, G., Ibrahimov, M., Asfandiyarov, I., Stoops, E., Eigenbrod, A., Le Guillou, L., van Winckel, H., and Magain, P., “COSMOGRAIL: the COSmological MOnitoring of GRAvItational Lenses. V. The time delay in SDSS J1650+4251”, Astron. Astrophys., 464, 845–851, (2007). ADS: http://adsabs.harvard.edu/abs/2007A&A...464..845V.
Walsh, D., Carswell, R.F., and Weymann, R.J., “0957 + 561 A, B: twin quasistellar objects or gravitational lens?”, Nature, 279, 381–384, (1979).
Wambsganss, J., “Gravitational Lensing in Astronomy”, Living Rev. Relativity, 1, lrr-1998-12, (1998). URL (cited on 25 June 2007): http://www.livingreviews.org/lrr-1998-12.
Wang, X., Wang, L., Pain, R., Zhou, X., and Li, Z., “Determination of the Hubble Constant, the Intrinsic Scatter of Luminosities of Type Ia Supernovae, and Evidence for Nonstandard Dust in Other Galaxies”, Astrophys. J., 645, 488–505, (2006). ADS: http://adsabs.harvard.edu/abs/2006ApJ...645..488W.
Wesselink, A.J., “Surface brightnesses in the U, B, V system with applications of MV and dimensions of stars”, Mon. Not. R. Astron. Soc., 144, 297–311, (1969). ADS: http://adsabs.harvard.edu/abs/1969MNRAS.144..297W.
Williams, L.L.R., and Saha, P., “Pixelated Lenses and H0 from Time-Delay Quasars”, Astron. J., 119, 439–450, (2000). ADS: http://adsabs.harvard.edu/abs/2000AJ....119..439W.
Winn, J.N., Kochanek, C.S., McLeod, B.A., Falco, E.E., Impey, C.D., and Rix, H.-W., “PKS 1830-211: A Face-on Spiral Galaxy Lens”, Astrophys. J., 575, 103–110, (2002). ADS: http://adsabs.harvard.edu/abs/2002ApJ...575..103W.
Wisotzki, L., Schechter, P.L., Bradt, H.V., Heinmüller, J., and Reimers, D., “HE 0435-1223: A wide separation quadruple QSO and gravitational lens”, Astron. Astrophys., 395, 17–23, (2002). ADS: http://adsabs.harvard.edu/abs/2002A&A...395...17W.
Wright, E.L., “Constraints on Dark Energy from Supernovae, Gamma Ray Bursts, Acoustic Oscillations, Nucleosynthesis and Large Scale Structure and the Hubble constant”, (2007). URL (cited on 08 May 2007): http://arXiv.org/abs/astro-ph/0701584.
Wucknitz, O., Biggs, A.D., and Browne, I.W.A., “Models for the lens and source of B0218+357: a LENSCLEAN approach to determine H0”, Mon. Not. R. Astron. Soc., 349, 14–30, (2004). ADS: http://adsabs.harvard.edu/abs/2004MNRAS.349...14W.
York, D.G., Adelman, J., Anderson, J.E., Anderson, S.F., Annis, J., Bahcall, N.A., Bakken, J.A., Barkhouser, R., Bastian, S., Berman, E., Boroski, W.N., Bracker, S., Briegel, C., Briggs, J.W., Brinkmann, J., Brunner, R., Burles, S., Carey, L., Carr, M.A., Castander, F.J., Chen, B., Colestock, P.L., Connolly, A.J., Crocker, J.H., Csabai, I., Czarapata, P.C., Davis, J.E., Doi, M., Dombeck, T., Eisenstein, D.J., Ellman, N., Elms, B.R., Evans, M.L., Fan, X., Federwitz, G.R., Fiscelli, L., Friedman, S., Frieman, J.A., Fukugita, M., Gillespie, B., Gunn, J.E., Gurbani, V.K., de Haas, E., Haldeman, M., Harris, F.H., Hayes, J., Heckman, T.M., Hennessy, G.S., Hindsley, R.B., Holm, S., Holmgren, D.J., Huang, C., Hull, C., Husby, D., Ichikawa, S., Ichikawa, T., Ivezić, Ž., Kent, S., Kim, R.S.J., Kinney, E., Klaene, M., Kleinman, A.N., Kleinman, S., Knapp, G.R., Korienek, J., Kron, R.G., Kunszt, P.Z., Lamb, D.Q., Lee, B., Leger, R.F., Limmongkol, S., Lindenmeyer, C., Long, D.C., Loomis, C., Loveday, J., Lucinio, R., Lupton, R.H., MacKinnon, B., Mannery, E.J., Mantsch, P.M., Margon, B., McGehee, P., McKay, T.A., Meiksin, A., Merrelli, A., Monet, D.G., Munn, J.A., Narayanan, V.K., Nash, T., Neilsen, E., Neswold, R., Newberg, H.J.M., Nichol, R.C., Nicinski, T., Nonino, M., Okada, N., Okamura, S., Ostriker, J.P., Owen, R., Pauls, A.G., Peoples, J., Peterson, R.L., Petravick, D., Pier, J.R., Pope, A., Pordes, R., Prosapio, A., Rechenmacher, R., Quinn, T.R., Richards, G.T., Richmond, M.W., Rivetta, C.H., Rockosi, C.M., Ruthmansdorfer, K., Sandford, D., Schlegel, D.J., Schneider, D.P., Sekiguchi, M., Sergey, G., Shimasaku, K., Siegmund, W.A., Smee, S., Smith, J.A., Snedden, S., Stone, R., Stoughton, C., Strauss, M.A., Stubbs, C.W., SubbaRao, M., Szalay, A.S., Szapudi, I., Szokoly, G.P., Thakar, A.R., Tremonti, C., Tucker, D.L., Uomoto, A., Vanden Berk, D.E., Vogeley, M.S., Waddell, P., Wang, S., Watanabe, M., Weinberg, D.H., Yanny, B., and Yasuda, N., “The Sloan Digital Sky Survey: Technical Summary”, Astron. J., 120, 1579–1587, (2000). ADS: http://adsabs.harvard.edu/abs/2000AJ....120.1579Y.
York, T., Jackson, N., Browne, I.W.A., Wucknitz, O., and Skelton, J.E., “The Hubble constant from the gravitational lens CLASS B0218+357 using the Advanced Camera for Surveys”, Mon. Not. R. Astron. Soc., 357, 124–134, (2005). ADS: http://adsabs.harvard.edu/abs/2005MNRAS.357..124Y.
Zaritsky, D., Kennicutt Jr, R.C., and Huchra, J.P., “H II regions and the abundance properties of spiral galaxies”, Astrophys. J., 420, 87–109, (1994). ADS: http://adsabs.harvard.edu/abs/1994ApJ...420...87Z.
Acknowledgements
I thank Nick Rattenbury, Sir Francis Graham-Smith and an anonymous referee for careful reading of, and comments on, the manuscript. I thank the Kavli Institute for Theoretical Physics, Santa Barbara, for hospitality during the early phase of the writing of this article. This article has made use of NASA’s Astrophysics Data System Bibliographic Services.
Author information
Authors and Affiliations
Corresponding author
A Highly Subjective Summary of the Gravitational Lens Time Delays to Date and the Derived Values of the Hubble Constant
A Highly Subjective Summary of the Gravitational Lens Time Delays to Date and the Derived Values of the Hubble Constant
All discussion is based on parametric models (though see the text for non-parametric models). For B0218+357 the mass-model is reasonably well known, thanks to an Einstein ring and VLBI structure [176] but the galaxy centre astrometry is not. York et al. [178] find 70 ±5 (2σ) based on an ACS determination of the galaxy centre, and Wucknitz et al. [176] find 78 ± 6 (2σ) using the ring and VLBI structure. I double the errors and take 74 ± 5. For HE0435−1223 the image positions of [174] with the lens redshift of [99] and the longest time delay of [79], together with an isothermal sphere model with external shear, gives H0 = 90, similar to the value inferred by Kochanek et al. A 20% error for the lack of knowledge of the mass profile and another 20% for the presence of nearby galaxies are added in quadrature to the time delay error to give H0 = 90 ± 26. For SBS0909+532 the system is very underconstrained, especially as the flux ratios are not well known, possibly due to extinction [166]. Lehár et al. [88] find a predicted time delay of 49 ± 38 days for H0 = 70, by considering the allowed space where χ2 < 1, the time delay of 45 days [166] translates into H0 = 76 ± 59; one might argue that the errors should be slightly smaller but this lens is not in any case going to contribute significantly to the overall total. In RXJ0911+0551 the situation is complicated by the presence of a nearby cluster. Hjorth et al. [55] obtain 71 ± 9 (2σ) based on a velocity dispersion for the cluster from [74] (but see also discussion in [77]). As with B0218+357 I double the errors and take 71 ± 9. In FBQ0951+2635 an isothermal model gives \(60_{- 7 - 2}^{+ 9 + 2}\) [68]. The same source claims that in this lens the variation of H0 with mass slope is relatively weak, but I nevertheless add an extra 20% to the error and take 60 ± 15. For Q0957+561, a system with a huge cluster contribution, probably the most compelling analysis (of the vast literature on this object) is that in [70] where the lensed host galaxy is used to disentangle the cluster shear from the internal shear produced by the lensed galaxy shape. Assuming a cluster convergence of 0.2, using the range of Keeton et al.’s sample models and increasing the errors by 20% gives 90 ± 25. For SDSS J1004+4112 the cluster contribution makes modelling so problematic that it is difficult to sort out sensible H0 estimates from simple models. However, once the cluster mass profile is thoroughly understood using the large number of constraints and the remaining time delays are known, this may give the best H0 estimate of all [42]. HE1104−185 is also a bizarre system in which the closer image is brighter; Lehár et al. [88] predict much larger time delays than are actually found, and typical isothermal models plus the time delay in [101] give H0 ∼ 95. For consistency I adopt this value, together with a 20% error added in quadrature to the time delay error to reflect the fact that we do not know the galaxy mass profile, giving 95±25. In PG1115+080 traditional fits of isothermal models give H0 in the forties [135], but a more recent stellar dynamical measurement [159] suggests a steeper-than-isothermal profile and with the time delay in [135] gives \({H_0} = 59_{- 7 - 3}^{+ 12 + 3}\), so I adopt 59 ± 12. In RXJ1131−1231 almost any smooth isothermal model fails (and H0 < 10), so Morgan et al. [98] suggest that a large piece of substructure or satellite galaxy falls close to one of the images. While plausible, this means that the system is almost impossible to model for H0. There is a measured time delay for JVAS B1422+231 [110] but in my view it needs confirmation before being used for H0 determination. SBS 1520+530 is modelled in [18], who also provide the time delay, by an isothermal model together with consideration of a nearby cluster. I add 20% to their error, due to the isothermal assumption, and get 51 ± 13. In B1600+434 an isothermal model gives \(60_{- 12}^{+ 16}\) (random errors [81], but adjusted for a (Ωm,Ωλ = (0.3, 0.7) model). I add 20% for systematics involved in lack of knowledge of the mass profile and get 60 ± 20. In B1608+656 Koopmans et al. [83] assemble an impressive array of data, including three time delays, stellar velocity measurements and Einstein ring fitting to get \(75_{- 6}^{+ 7}\), to which I add another 10% due to a feeling of unease about the lens being two interacting galaxies and consequent effects on the mass profile, and take 75 ± 10. For SDSS J1650+4251 I adopt the value of H0 = 52 from the time delay and isothermal models of [167], plus an extra 20% error for the mass slope, and use H0 = 52 ± 11. In PKS1830−211 models in [173] using their improved galaxy centre position give 44 ± 9, to which I add the now traditional 20% for ignorance of the mass slope and 10% (cf. B1608+656) for the possibility of associated secondaries [25], to give 44 ± 13. Finally, for HE2149-2745, a simple SIE model gives H0 = 49, in agreement with the average of \(48_{- 4}^{+ 7}\) quoted in [76] on analysis of this plus four other lenses; Burud et al. [17] derive a higher value due to restrictions on assumed ellipticity of the lens galaxy. Adding the usual 20% for ignorance of the mass slope to the time delay error we obtain 49 ± 11. At last, the overall average is 66 ± 3 (or 61 ± 4 without B0218+357). We should also consider the effect of mass along the line of sight, which is likely to add a further 5–10% to the error budget of each lens system and which will probably not reduce as \(\sqrt n\); much of it is systematic if the error is normally in the sense of ignoring nearby groups of matter which add to the local convergence.
It should be emphasised that this is an attempt to work out one observer’s view of the situation based on parametric models, and that the reader will have noticed a lot of subjective judgements and arbitrary manipulation of errors going on, but you did ask.
Rights and permissions
This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Jackson, N. The Hubble Constant. Living Rev. Relativ. 10, 4 (2007). https://doi.org/10.12942/lrr-2007-4
Accepted:
Published:
DOI: https://doi.org/10.12942/lrr-2007-4
Keywords
Article history
Latest
The Hubble Constant- Published:
- 24 September 2015
- Accepted:
- 14 August 2014
DOI: https://doi.org/10.1007/lrr-2015-2
Original
The Hubble Constant- Published:
- 24 September 2007
- Accepted:
- 11 September 2007
DOI: https://doi.org/10.12942/lrr-2007-4