INTRODUCTION

Pattern recognition is a key element in pharmacokinetic data analyses when first selecting a model to be regressed to data. We call this process going from data to insight. But there are no formal best practices that scientists typically use. This report deals with identifying the properties of a kinetic model by dissecting the pattern that concentration-time data reveal graphically. Pattern recognition is a pivotal activity when modeling pharmacokinetic data, because a rigorous strategy is essential for dissecting the determinants behind concentration-time courses. In the pharmacology field, pattern recognition has also been proposed for interpreting results of drug-drug interactions (1).

The format of the presentation order of the data sets are shown in Fig. 1. The route of administration is the top level. Under that, we split into intravenous (iv, disposition kinetics) dosing and extravascular (ev, po, absorption confounded kinetics) of single- (mono-exponential decline) and multiple-compartment (multi-exponential decline) systems. The next level discriminates between linear- and nonlinear systems. This order is, what we assume, that one immediately can see from a semi-logarithmic graph of concentration-time data. A special case of extravascular administration where one has to discriminate between first- and zero-order input is also given.

Fig. 1
figure 1

Decision-tree structure of the analyzed case studies. Numeralrefer to the case studies.

Full size image

The 16 data schemes we are going to discuss are shown schematically in Fig. 2. These are representative of different patterns typically seen in in vivo pharmacokinetic practice. For each case study, we will provide the underlying model including the differential equations that describe the system, the parameters and constants, and the number of functions (datasets) involved in the regression analysis.

Fig. 2
figure 2

Schematic illustration of the 16 data patterns discussed in this report. 1 Two individuals with mono-exponential disposition. 2 Bi-exponential decline after iv bolus dosing in two groups of animals. 3 Lag time or no lag time in the absorption process with absorption rate-limited elimination. 4 Simultaneous analysis of bi-exponential decline after iv dosing and mono-exponential decline when dosing orally. 5 Multi-exponential behavior after oral dosing. 6 Plasma and cumulative urine data. 7 Single-compartment disposition coupled to nonlinear elimination. 8 Multi-compartment disposition coupled to nonlinear elimination. 9 Nonlinear elimination after oral dosing. 10 Saturable absorption by transporters. 11 Bi-exponential decline after bolus dosing with a baseline value. 12 Extravascular administration of an endogenous compound with a baseline value. 13 Target-mediated drug disposition. 14 Multiple dosing coupled to a period of hetero-induction shown by the gray horizontal bar. 15 Nonlinear formation of metabolite (dashed lines) after iv dosing of parent compound (solid lines). 16 First- and zero-order absorption patterns. All plots are semi-logarithmic except 12, 14, and 16 where data are displayed on a linear scale due to a limited concentration range.

Full size image

The following strategy was adopted:

  • In case studies 1 and 2, we explore intravenous iv bolus dosing of a one (two subjects with different clearances and similar volumes) and two compartments (two populations, clamped and normal with different clearances and effective half-lives).

  • Then, we move on to extravascular dosing in case studies 3 and 4, where a one-compartment first-order input/output systems with and without lag time, and iv and extravascular dosing for a two-compartment system, respectively.

  • In case study 5, we revisit extravascular (po) dosing although we observe rapid absorption, lag time, and multi-exponential decline post-peak. This dataset does not contain iv data.

  • Case study 6 returns to iv bolus dosing and mono-exponential decline in plasma but is extended also with urinary data so renal clearance or fraction excreted into the urine can be estimated simultaneously with total clearance.

  • Case studies 7 and 8 are also iv dosing covering mono- and bi-exponential decline for two systems that exhibit saturable (nonlinear) clearance terms.

  • Two nonlinear systems are also presented after oral dosing in case studies 9 and 10. The former captures nonlinear elimination and the latter saturable absorption via transporters.

  • We extend the analyses by looking at iv (case study 11) and subcutaneous (sc) (case study 12) of two systems with endogenous levels of the test compound. This extends the model with one additional parameter, the turnover rate.

  • The last four case studies (case studies 13–16) are extensions looking at target-mediated drug disposition (case study 13), time-dependent induction of clearance (case study 14), simultaneous fitting of nonlinear multi-compartment kinetics of parent compound and metabolite after three different iv doses, and then finally fitting a first- and zero-order absorption model to an oral dosing dataset.

We encourage the analyst to regress several sources of data simultaneously if possible. In case study 4, a full two-compartment system is revealed in iv data but not in ev data. This dataset is contrasted with case study 5 where only ev data are available. However, the latter still displays a multi-compartment behavior due to the rapid absorption. Both case studies 4 and 5 are commonly encountered situation which is the reason why they may be of interest to the reader. Several sources of data are further elaborated on in case studies 6, 7, 9, 10, 13, and 15. Further comparisons across two or more case studies are done at the end of relevant cases.

A schematic diagram of each model proposed for the data schemes in Fig. 2 is shown in Fig. 3.

Fig. 3
figure 3

Schematic diagram of each model used for the analysis of concentration-time data shown in Figs. 2, 4, 5, 6, and 7. All parameters and variables are explained in their respective case study sections. Numerals above the figures refer to the respective case study.

Full size image

A set of points to consider are proposed that specifically addresses exploratory data analyses, number of phases in the concentration-time course, convex or concave curvature, baseline behavior, time delay, lag time, peak shifts with increasing doses, flip-flop phenomena, saturation, and other potential nonlinearities that the eye catches in the data. We look at what causes the shapes that make up the concentration-time course. By practicing pattern recognition, one can significantly improve the quality of data analysis and model building. A consequence of this is a better understanding of the complete concentration-time profile. We have therefore collected a set of patterns extracted from literature data and then modified them so the typical features emerge more clearly (2). We also propose alternative solutions to the patterns.

The number of parameters NP which can be calculated for a given model is dependent on the number of exponentials EX post-peak visible in the plasma concentration-time profile, the number of elimination or excretory pathways PE suitably measured, the number of tissue spaces or binding proteins TS analyzed, and the number of visible nonlinear features NL in the data (Eq. 1, top). This expression was proposed by Jusko and meant to be a guidance function (a set of numerical points to consider) when dissecting pharmacokinetic profiles (3). We have personally benefitted from this simple but elegant tool as a starting point in our own analyses. An extension (Eq. 1, bottom) of the original model is presented here which also includes information about absorption ABS, initial time delays TLG, baseline BL, and potential metabolite(s) MTB

$$ \left\{\begin{array}{l}\mathrm{Original}\ \mathrm{model}\kern0.75em \mathrm{N}\mathrm{P}=2\cdot \mathrm{EX}+\mathrm{P}\mathrm{E}+2\cdot \mathrm{T}\mathrm{S}+\mathrm{N}\mathrm{L}\\ {}\\ {}\mathrm{E}\mathrm{xtended}\ \mathrm{model}\kern0.5em \mathrm{N}\mathrm{P}=2\cdot \mathrm{EX}+\mathrm{P}\mathrm{E}+2\cdot \mathrm{T}\mathrm{S}+\mathrm{N}\mathrm{L}+\mathrm{ABS}+\mathrm{T}\mathrm{L}\mathrm{G}+\mathrm{B}\mathrm{L}+2\cdot \mathrm{M}\mathrm{T}\mathrm{B}\end{array}\right. $$
(1)

Equation 1 is applicable if sufficient and accurate data are obtained and can be extended. For example, if we have data after an intravenous bolus dose that decline in a bi-exponential fashion (i.e., with an α and a β phase), then it is possible to estimate 2 EX = 4 parameters (i.e., A, α, B, and β). If we also have measured drug excretion in urine, we could estimate renal clearance or fraction of dose excreted via the urine PE. If, in addition to the bi-exponential decline in plasma 2 EX, we have a nonlinear feature NL and urinary data PE, we might be able to estimate six parameters.

Equation 1 was suggested as a practical tool for the identification of a possible number of estimable parameters based on observable patterns of the drug moiety as such in plasma. We will also see how applicable the extended Eq. 1 is to the 16 datasets provided. Equation 1 should be used with careful attention to the quality of data, the design of the experiment, and when the number of data sources beyond parent compound in plasma and urine are available. Simultaneous fitting of all available sources of data is always recommended.

This report focuses on the practical identifiability of pharmacokinetic parameters based on visual inspection of experimental data. First, we extend a commonly used relationship for calculation of the number of potential model parameters by simultaneously utilizing all concentration-time courses. Then, a set of points to consider is proposed that specifically addresses exploratory data analyses, number of phases in the concentration-time course, baseline behavior, time delays, peak shifts with increasing doses, flip-flop phenomena, saturation, and other potential nonlinearities that an experienced eye catches in the data. Finally, we set up a series of equations related to the patterns and themes. Theoretical a priori identifiability of pharmacokinetic parameters has been discussed by others (4) and will not be addressed here.

Case study 1

A mono-exponential decline is observed in plasma after an intravenous bolus dose to two subjects (Fig. 4, case study 1 (2)). Both subjects received the same amount of test compound. The goal is to identify typical signs of pharmacokinetic similarities and differences between these two concentration-time courses. In other words, what are the most obvious characteristics that one may pick out by visual inspection of data?

Fig. 4
figure 4

Case study 1 Semi-logarithmic plot of concentration-time data in two subjects after a rapid intravenous injection of the same dose. An apparent mono-exponential decline is shown in plasma corresponding to a one-compartment system. The back-extrapolated concentration at time zero is approximately 1000 μg L−1 in both subjects suggesting the same volume of distribution. Clearance Cl of test compound is larger in subject 2 which is manifested in a smaller area-under-the plasma concentration-time curve AUC and a shorter half-life (35 min) as compared to subject 1 (65 min). Case study 2 Semi-logarithmic plot of concentration-time data in two groups of rats after a rapid intravenous injection of the same dose of recombinant human superoxide dismutase (rh-SOD). An apparent bi-exponential decline is shown in plasma corresponding to a two-compartment system (right). The back-extrapolated concentration at time zero is approximately 1000 μg mL−1 in both groups suggesting similar central volumes of distribution. Clearance Cl of the test compound is larger in normal rats which is manifested in a smaller AUC. The small red arrows indicate the elimination phase in normal (initial phase) and clamped (diseased, terminal phase) rats. The effective half-life is about 10 min (close to initial phase) in normal animals as compared to 90 min (terminal phase) in clamped animals. Cl d , V c, and V t denote inter-compartmental distribution parameter and central and peripheral volume terms, respectively. V ss is the sum of the two volume terms. Case study 3 Semi-logarithmic plot of concentration-time data in one subject after an oral dose. An apparent initial delay in the rise of plasma test compound concentrations is followed by a rapid initial upswing with a C max at about 60 min and then a post-peak mono-exponential decline corresponding to a one-compartment input/output system (right). Superimposed on experimental data (filled symbols) are the lag time and no lag time model fits. Note how the lack of a lag time misses the initial 10–20-min delay, the rise in experimental data, the peak concentration, and over predicts the terminal time points. A tentative time course after intravenous administration is shown as a dotted red line. This implies that the terminal portion of oral data shows absorption rate-limited elimination—flip-flop pharmacokinetics. Cl, F, K a, and t lag denote clearance, bioavailability, absorption rate constant, and lag time, respectively. Case study 4 Semi-logarithmic plot of concentration-time data in one subject after intravenous and oral dosing at two different occasions. Intravenous data (solid squares) display a bi-exponential decline which suggests a typical two-compartment disposition (see model inset). Oral data shows an apparent initial delay in the rise of plasma test compound concentrations which is then followed by a rapid initial upswing with a C max at about 50 min and then a post-peak weak bi-exponential decline (solid circles). Data from both routes of administration were simultaneously fit by the two-compartment model with either bolus or first-order input. Cl, V c, V t, Cl d , F, and K a denote clearance, central volume, peripheral volume, inter-compartmental distribution, bioavailability, and absorption rate constant, respectively.

Full size image

The mono-exponential decline shown in Fig. 4 (case study 1) on logarithmic concentration scale can be described mathematically as a first-order differential equation.

$$ \frac{dC}{dt}=-K\cdot C=-\frac{\mathrm{Cl}}{V}\cdot C $$
(2)

dC/dt is the rate of change of the plasma concentration, C is the plasma concentration, and K is the first-order rate constant associated with the elimination process. A new parameter, clearance Cl, is then introduced. Clearance is defined as the volume of blood or plasma that is totally cleared of its content of drug per unit time (mL min−1 or L min−1). The other parameter of primary interest is the volume of distribution V. This is the apparent space that test compound distributes into.

The solid lines in Fig. 4 show the behavior of Eq. 2. This equation is actually a mathematical interpretation of many first-order exponential processes in the body (loss of water, decline of hormones, food constituents). We also observe that the two subjects have approximately the same intercept, C(0), suggesting similar volumes. Dose and volume determine the intercept after an iv bolus dose. The area under the concentration-time curve AUC for subject 2 is less than the area under subject 1 in spite of equal doses. This is due to the larger clearance for subject 2 than subject 1. Clearance and dose determine the area. Consequently, the half-life will be shorter for subject 2 (35 min) as compared to subject 1 (65 min) (Eq. 3), which is also clearly observed in the plot.

$$ {t}_{1/2}= \ln (2)\cdot \frac{V}{\mathrm{Cl}} $$
(3)

Should the two subjects have had the same clearance but different volumes, the AUCs would have been the same and the intercepts different. So, by inspecting the shapes (slopes and intercepts and areas), one can make conclusions about the relative clearances and volumes.

The key features of this pattern are mono-exponential decline in plasma of two subjects with different clearances and same volumes. Applying Eq. 1, the number of parameters NP that can be estimated from the data is two for each subject (=2 EX such as Cl and V or K and V).

Case study 2

A bi-exponential decline is observed in plasma after an intravenous bolus dose to two different populations of rats (Fig. 4, case study 2 (2)). Both populations received the same amount of test compound (20 mg). Test compound is a large molecular weight chemical which is primarily cleared via the kidney and a small fraction is metabolized. One group of rats (denoted diseased animals) had the blood supply to and from the kidneys shut off by a clamp.

The bi-exponential decline observed in Fig. 4 (case study 2) displays two distinct phases, one initial with rapid decline and a terminal phase with slower decline as shown on the logarithmic concentration scale. The relationship between the concentration C and the rate of change dC/dt in plasma and tissue can be expressed mathematically as a system of two differential equations for a two-compartment model with first-order kinetics, when drug is administered as a bolus dose into the gut as follows:

$$ \left\{\begin{array}{l}{V}_{\mathrm{c}}\cdot \frac{dC}{dt}=-\mathrm{C}\mathrm{l}\cdot C-{\mathrm{Cl}}_d\cdot C+{\mathrm{Cl}}_d\cdot {C}_{\mathrm{t}}\\ {}\\ {}{V}_t\cdot \frac{d{C}_t}{dt}={\mathrm{Cl}}_d\cdot C-{\mathrm{Cl}}_d\cdot {C}_{\mathrm{t}}\end{array}\right. $$
(4)

dC/dt and dC t /dt are the rate of change of test compound in plasma and tissue compartments, C is the plasma concentration, C t the tissue concentration, Cl plasma clearance, V c central volume, V t peripheral volume, and Cl d the inter-compartmental distribution parameter. Cl d has the units of volume per time (mL min−1 or L min−1) and is related to transport of test compound out into the tissues via the blood flow, transporters, and diffusion/convection forces. The total volume of distribution V ss is the sum of V c and V t, which is the apparent space that test compound distributes into in a two-compartment system.

The solid lines in Fig. 4 (case study 2) show the behavior of Eq. 4. This equation is a mathematical approximation of many first-order bi-exponential processes in the body (such as estradiol, hyaluronan). We also observe that the two groups have approximately the same terminal slope, −β, and normal animals have a slightly lower intercept of the concentration axis which suggests a slightly higher central volume V c compared to the clamped animals. This is a consequence of clamping blood supply to and from the kidneys resulting in a removal of a substantial blood volume. The AUC in normal animals is much less than the area under clamped animals in spite of equal doses. This is due to the fact that normal animals have a much larger (uncompromised) clearance than clamped animals. Due to the large differences in clearance, the effective half-life t 1/2(e) will be shorter in normal animals (10 min) as compared to clamped animals (90 min) (Eq. 5).

$$ {t}_{1/2}(e)= \ln (2)\cdot \frac{V_{\mathrm{ss}}}{\mathrm{Cl}} $$
(5)

We typically observe and measure what is going on in the central compartment represented by plasma, but we need the additional peripheral compartment to make up for the two phases observed in the plasma concentration-time course and the input rate from the gastrointestinal region. In this case study, there is still a distinct difference between the initial and terminal phases. In other situations, one may want to reduce or increase the number of exponentials. Model discrimination then has to be based on residual analysis, goodness-of-fit criteria (objective function value, Akaike information criterion), parameter precision, and correlation (see Gabrielsson and Weiner, 2010, for a discussion (2)).

The key features of the studied patterns are bi-exponential decline in plasma of two groups of animals with different clearances. In spite of similar terminal half-lives, their effective half-lives differ almost tenfold. If we then apply Eq. 1, the number of estimable parameters is four (=2 EX = 2 × 2 = 4 namely Cl, Cl d , V c, and V t).

Case study 3

This case study deals with a typical pattern observed for an orally administered test compound that displays a delay in the onset of absorption. Experimental data are shown together with two model-predicted time courses in Fig. 4 (case study 3 (2)). The most obvious signature in experimental data is a slight time delay of 10–20 min before plasma test compound concentrations start to rise, followed by a rapid rise and a peak concentration at about 60 min. Experimental data are then obtained up to 6 h after dosing. By plotting the data on a semi-logarithmic scale, one observes a mono-exponential post-peak decline which suggests that a one-compartment model with first-order input (absorption) / output (elimination) may be a good start. Data reveal that when the terminal phase is compared to the disposition of test compound after intravenous dosing absorption rate-limited elimination prevails.

The relationship between the concentration C and the rate of change dC/dt in concentration may be expressed mathematically as a one-compartment model with first-order input/output kinetics when drug is administered as a bolus dose as follows:

$$ \left\{\begin{array}{l}V\cdot \frac{dC}{dt}=F\cdot {K}_{\mathrm{a}}\cdot {D}_{\mathrm{po}}\cdot {e}^{-{K}_a\cdot t}-\mathrm{C}\mathrm{l}\cdot C\hfill \\ {}V\cdot \frac{dC}{dt}=F\cdot {K}_{\mathrm{a}}\cdot {D}_{\mathrm{po}}\cdot {e}^{-{K}_a\cdot \left(t-{t}_{\mathrm{lag}}\right)}-\mathrm{C}\mathrm{l}\cdot C\hfill \end{array}\right. $$
(6)

dC/dt is the rate of change of the plasma concentration, C is the plasma concentration, F is bioavailability, K a absorption rate constant, V volume, and Cl is clearance (or reparameterized with the elimination rate constant K = Cl/V) associated with the elimination process. D po and t lag denote oral dose and lag time, respectively.

In this case study, there is a distinct difference between the lag time (model of choice) and no lag time models (systematic deviations throughout the model-predicted concentration-time course), which is already shown in the function plots. In other cases, this may not be so obvious and model discrimination then has to be based on residual analysis, goodness-of-fit criteria (objective function value, Akaike information criterion), parameter precision, and correlation (see Gabrielsson and Weiner, 2010, for a discussion (2)).

The key features of the studied patterns are a lag time before the onset of absorption, then a rapid initial rise to C max and mono-exponential decline post-peak. The importance of adding a lag time to the model is shown in the two fitted models superimposed on experimental data. If we then apply the extended Eq. 1 with necessary parameters for the present dataset, we get

$$ \mathrm{N}\mathrm{P}=\mathrm{ABS}+\mathrm{T}\mathrm{L}\mathrm{G}+2\cdot \mathrm{EX}=1+1+2\cdot 1=4 $$
(7)

Four parameters that are estimable from the data (K a, t lag, K, and V/F). For this case study, absorption rate-limited elimination is shown in the terminal portion of the oral data—also known as the flip-flop pharmacokinetics.

Case study 4

This dataset shows a bi-exponential decline after intravenous dosing which is very much masked when test compound is given via the oral route (Fig. 4, case study 4 (2)). If the rate of absorption is relatively slow, oral data typically display a mono-exponential decline post-peak. When iv data are added to the picture, a clearer picture of the two-compartment disposition emerges. Iv data are needed to correctly analyze the po data which shows a weak tendency of bi-exponential decline after C max. We may also want to fit a lag time model for the oral absorption process.

The bi-exponential decline observed in Fig. 4 (case study 4) displays two distinct phases after intravenous dosing, one initial with rapid decline and a terminal phase with slower decline more clearly displayed on a logarithmic concentration scale. The two phases are separated by a concave bend in the curve at about 40–60 min. The relationship between the concentration C and the rate of change dC/dt in plasma and tissue after intravenous and extravascular dosing can be expressed mathematically as a system of two differential equations for a two-compartment model with first-order kinetics, when drug is administered as a bolus dose as follows:

$$ \left\{\begin{array}{l}{\mathrm{Input}}_{\mathrm{iv}}=\mathrm{Bolus}\hfill \\ {}{\mathrm{Input}}_{\mathrm{po}}=F\cdot {D}_{\mathrm{po}}\cdot {K}_{\mathrm{a}}\cdot {e}^{-{K}_{\mathrm{a}}\cdot t}\hfill \\ {}{V}_c\cdot \frac{dC}{dt}=\left(\begin{array}{l}{\mathrm{Input}}_{\mathrm{iv}}\\ {}\mathrm{or}\\ {}{\mathrm{Input}}_{\mathrm{po}}\end{array}\right)-\mathrm{C}\mathrm{l}\cdot C-{\mathrm{Cl}}_d\cdot C+{\mathrm{Cl}}_d\cdot {C}_{\mathrm{t}}\hfill \\ {}{V}_t\cdot \frac{d{C}_{\mathrm{t}}}{dt}={\mathrm{Cl}}_d\cdot C-{\mathrm{Cl}}_d\cdot {C}_{\mathrm{t}}\hfill \end{array}\right. $$
(8)

Inputpo, F, D po, and K a are the input rate, bioavailability, oral dose, and absorption rate constant, respectively. The dC/dt and dC t /dt are the rate of change of test compound in plasma and tissue, C is the plasma concentration, C t the peripheral concentration, Cl plasma clearance, V c central volume, V t peripheral volume, and Cl d the inter-compartmental distribution parameter.

We typically observe and measure what is going on in the central compartment represented by plasma, but we need the additional peripheral compartment to make up for the two phases observed in the plasma concentration-time course and the input rate from the gastrointestinal region.

The higher the absorption rate constant, the greater is the chance of observing a multi-exponential decline post-peak. In Fig. 5, simulated data of intravenous and oral dosing are superimposed using three oral absorption rate constants (fast, intermediate, and slow). Note how the oral concentration-time profile having a high K a and displaying a bi-exponential decline post-peak (multi-compartment characteristics) turns into a one-compartment input/output profile similar to a one-compartment model as shown in Fig. 4 when the absorption rate constant is low.

Fig. 5
figure 5

Semi-logarithmic plot of simulated concentration-time data after intravenous dosing (bi-exponential decline bending at 50 min) and oral dosing with three different absorption rate constants K a. The oral profile displays bi-phasic decline post-peak when absorption rate is high and mono-exponential decline post-peak when the absorption rate is low which then masks disposition.

Full size image

The key features of the studied patterns are multi-exponential decline observed after intravenous dosing and barely visible bi-phasic decline upon oral dosing. The latter is due to slow absorption relative to disposition. Absorption occurs after a time lag; the concentration-time profile peaks at about 50 min and then decline in a barely visible bi-phasic manner. Again, applying the extended Eq. 9 to both intravenous and oral data gives

$$ \mathrm{Extended}\ \mathrm{model}\kern0.5em \mathrm{N}\mathrm{P}=2\mathrm{EX}+2\mathrm{ABS}+\mathrm{T}\mathrm{L}\mathrm{G}=2\times 2+2\times 1+1=7 $$
(9)

The number of estimable parameters from data is then seven, namely Cl, Cl d , V c, V t, F, K a, and t lag.

Case study 5

This case study demonstrates data obtained from a calcium-channel blocker with a rate of absorption that exceeds the rate of disposition (distribution into tissues and elimination) (Fig. 6, case study 5 (2)). We will therefore be able to observe its bi-exponential decline beyond the peak concentration C max. These kind of data are often seen in both preclinical and clinical studies and differentiate themselves from data of case study 4 where also iv data are needed to correctly analyze po data with the weak bi-exponential decline post-peak. Intravenous data are still needed in order to discriminate between distribution and elimination, and for assessment of absolute bioavailability. We intentionally call the three phases initial, intermediate, and terminal phase.

Fig. 6
figure 6

Case study 5 Semi-logarithmic plot of observed (solid symbols) and model-predicted (line) concentration-time data in one subject after oral dosing. Data shows no delay prior to the rapid rise in plasma test compound concentrations with a C max at about 30 min. The post-peak data displays a bi-exponential decline. The red dashed line is the time course of an extended release dosage formulation with a slow absorption rate resulting in a late peak. The absorption is faster than the elimination since both curves fall in parallel terminally. Also, note the lack of the initially high concentration peak which the extended release will mask due to a slow release rate from the dosage form. Cl, V c, V t, Cl d , F, and K a denote clearance, central volume, peripheral volume, inter-compartmental distribution, bioavailability, and absorption rate constant, respectively. Case study 6 Semi-logarithmic plot of observed (solid symbols) and model-predicted (lines) concentration-time data in plasma and accumulated amount in urine of compound X. Plasma data displays a mono-exponential decline. ClR and Clm denote renal and metabolic clearance. Case study 7 Semi-logarithmic plot of observed (solid symbols) and model-predicted (lines) total concentration-time data in two subjects after intravenous dosing of 25 and 100 mg of test compound. Data display a convex decline with steeper slopes as concentration declines. Clearance ClMM is a function of maximum rate of elimination V max, the Michaelis-Menten constant K m, and plasma concentration C. Case study 8 Semi-logarithmic plot of observed (solid symbols) and model-predicted (lines) ethanol concentration-time data in one subject after an intravenous infusion (double arrow) of 0.4 g per kg body weight for 30 min. Clearance ClMM is a function of maximum rate of elimination V max, the Michaelis-Menten constant K m, and plasma concentration C. The horizontal dashed red line shows the estimated concentration of K m. ClMM, V c, V t, and Cl d denote the Michaelis-Menten clearance function, central volume, peripheral volume, and inter-compartmental distribution, respectively.

Full size image

The relationship between the concentration C and the rate of change dC/dt in plasma and tissue after extravascular dosing can be expressed mathematically as a system of two differential equations for a two-compartment model with first-order kinetics as follows:

$$ \left\{\begin{array}{l}{\mathrm{Input}}_{\mathrm{po}}=F\cdot {D}_{\mathrm{po}}\cdot {K}_{\mathrm{a}}\cdot {e}^{-{K}_{\mathrm{a}}\cdot t}\hfill \\ {}{V}_{\mathrm{c}}\cdot \frac{dC}{dt}={\mathrm{Input}}_{\mathrm{po}}-\mathrm{C}\mathrm{l}\cdot C-{\mathrm{Cl}}_d\cdot C+{\mathrm{Cl}}_d\cdot {C}_{\mathrm{t}}\hfill \\ {}{V}_t\cdot \frac{d{C}_{\mathrm{t}}}{dt}={\mathrm{Cl}}_d\cdot C-{\mathrm{Cl}}_d\cdot {C}_{\mathrm{t}}\hfill \end{array}\right. $$
(10)

Inputpo, F, D po, and K a are the input rate, bioavailability, oral dose, and absorption rate constant, respectively. The dC/dt and dC t /dt are the rate of change of compound in plasma and tissue, C is the plasma concentration, C t the peripheral concentration, Cl plasma clearance, V c central volume, V t peripheral volume, and Cl d the inter-compartmental distribution parameter.

We first fitted a no lag time model to the data which then failed to acceptably fit the upswing, peak, and initial post-peak phase. By adding a lag time, the systematic deviations were removed.

The key patterns of this dataset are rapid initial rise in exposure followed by a bi-exponential decline post-peak. A multi-exponential absorption/disposition model will capture this pattern. A three-exponential model or a two-compartment model with first-order input may suffice for capturing the data. No mechanistic interpretation of clearance or volume terms is possible since intravenous data and absolute bioavailability are lacking. Applying the extended Eq. 1 to both intravenous and oral data gives

$$ \mathrm{N}\mathrm{P}=\mathrm{ABS}+\mathrm{T}\mathrm{L}\mathrm{G}+2\cdot \mathrm{EX}=1+1+2\cdot 2=6 $$
(11)

The number of estimable parameters from data is six, namely Cl/F, Cl d /F, V c/F, V t/F, K a, and t lag.

Case study 6

Data were collected from both plasma and urine after an intravenous bolus dose of test compound X (Fig. 6, case study 6 (2)). A mono-exponential decline in plasma concentration coupled to cumulative amount in urine was modeled by a one-compartment drug model with a urine compartment as one of the elimination pathways. Plasma and urinary data were simultaneously fitted by a simple differential equation model (Eq. 12).

The differential equation that describes the plasma compartment and accumulated amount in urine are defined as

$$ \left\{\begin{array}{l}V\cdot \frac{dC}{dt}=-\mathrm{C}\mathrm{l}\cdot C\hfill \\ {}\frac{d{A}_u}{dt}={f}_e\cdot \mathrm{C}\mathrm{l}\cdot C={\mathrm{Cl}}_R\cdot C\hfill \end{array}\right. $$
(12)

A model for cumulative amount of drug excreted into urine is selected in combination with the one-compartment plasma model. Equation 12 includes three parameters, of which Cl occurs in both the plasma and cumulative urine equations. Therefore, try whenever possible to utilize as many sources of data (such as plasma concentrations and urine amounts) simultaneously when fitting a model to the data to increase accuracy and precision of the parameter estimates. The model for cumulative amount in urine has a very robust model structure and generally allows accurate and precise estimation of f e or Cl R in our experience.

The key features of this analysis are a combined plasma concentration and urinary excretion model that was simultaneously fit to two sources of time series. Key patterns are mono-exponential decline in plasma and a smooth first-order rise in cumulative amounts in urine. Volume and clearance are related to both datasets. Applying the extended Eq. 1 to both intravenous and urinary data gives

$$ \mathrm{N}\mathrm{P}=2\cdot \mathrm{EX}+\mathrm{P}\mathrm{E}=2\cdot 1+1=3 $$
(13)

The number of estimable parameters from data is three, namely Cl, V, and Cl R or f e .

Case study 7

A convex decline is observed in two concentration-time profiles after intravenous dosing of two doses to two individuals (Fig. 6, case study 7 (2)). This pattern shows a typical signature that cannot be modeled by adding more exponential terms. Since the slope of decline gets shallower in both subjects the higher the plasma concentration becomes, it suggests some kind of nonlinearity in possibly the elimination process. One typically would think of capacity-limited elimination (often called dose or concentration-dependent elimination), but if total concentrations are displayed, this could also be explained by saturable plasma protein binding. In this case study, we fit a model with capacity-limited (Michaelis-Menten) elimination to the data. Note that the terminal portions of the concentration-time courses have different slopes. Dose-normalized concentrations displayed the same initial concentration but deviated from each other during the remaining concentration-time courses. We suggest that volume V and maximum rate of elimination V max are the same for the two subjects but that their K m values differ since total concentration-time data are available for this highly plasma-bound test compound. The underlying assumption is that K m is more affected by plasma protein binding differences across subjects than V max. We also tested using the same K m but different V max parameters for the two subjects but that failed to produce an acceptable fit (see Gabrielsson and Weiner, 2010, for a detailed description of the analysis).

The plasma equation following intravenous administration is written as

$$ \left\{\begin{array}{l}V\cdot \frac{dC}{dt}=-{\mathrm{Cl}}_{\mathrm{MM}}\cdot C\hfill \\ {}{\mathrm{Cl}}_{\mathrm{MM}}=\frac{V_{\max }}{K_{\mathrm{m}}+C}\hfill \end{array}\right. $$
(14)

C and ClMM are the plasma concentrations and Michaelis-Menten type of capacity-limited clearance, respectively, and V max and K m are maximum rate of elimination and the Michaelis-Menten constant. It is the Michaelis-Menten expression in Eq. 14 that allows the model to capture the lack of superposition across doses and the time-dependent half-life.

The key features of these patterns are analysis of two concentration-time profiles that both display a convex shape of decline. Dose-normalized concentrations superimpose only at C(0) and deviate beyond that time point. A multi-phasic concave pattern was observed which typically occurs in nonlinear capacity-limited elimination. Both profiles declined in a linear fashion at low plasma concentrations. A successful attempt was made to simultaneously fit the two time courses with a common value for both subjects for the V max and volume V parameters but two different K m values. Applying the extended Eq. 1 to both intravenous time courses gives

$$ \mathrm{N}\mathrm{P}=2\cdot \mathrm{EX}+{\mathrm{NL}}_1+{\mathrm{NL}}_2=2\cdot 1+1+1=4 $$
(15)

NL1 and NL2 are the observed different nonlinear placements in the two datasets that Eq. 14 was simultaneously fitted to. The number of estimable parameters from data is four, namely V max, V, K m1, and K m2.

Case study 8

The kinetics of ethanol was characterized following a 30-min constant rate intravenous infusion (Fig. 6, case study 8 (5)). A number of volunteers were infused intravenously with a dose of 0.4 g ethanol per kg body weight. Plasma samples were obtained for 7 h. Ethanol displayed capacity-limited clearance and a volume of distribution equal to total body water. This problem highlights some of the complexities in modeling multi-compartment disposition with nonlinear capacity-limited elimination. For details about study design and a review of ethanol kinetics, see Norberg et al. (5,6).

The constant rate infusion of ethanol occurred over 30 min. Post-infusion data display initially a small concave shape followed by a slow extended convex decline with steeper slopes as concentration declines. The rapid post-infusion concave bend suggests an additional compartment beyond plasma that ethanol distributes into. It is well known that ethanol distributes into total body water (a 40-L volume in a 70-kg person). The top portion of the second phase after the stop of infusion is shallow and starts to bend down with a steeper slope as concentrations decline. This convex bend suggests some kind of nonlinearity that excludes binding changes. Saturation of the metabolizing enzymes are well known for ethanol above 30 μg L−1. Therefore, a Michaelis-Menten type of expression of clearance was included into the model (Eq. 16).

$$ \left\{\begin{array}{l}{V}_{\mathrm{c}}\cdot \frac{dC}{dt}=\mathrm{In}-\mathrm{C}\mathrm{l}\cdot C-{\mathrm{Cl}}_d\cdot C+{\mathrm{Cl}}_d\cdot {C}_{\mathrm{t}}\\ {}\\ {}{V}_{\mathrm{t}}\cdot \frac{d{C}_t}{dt}={\mathrm{Cl}}_d\cdot C+{\mathrm{Cl}}_d\cdot {C}_{\mathrm{t}}\\ {}\\ {}\mathrm{C}\mathrm{l}=\frac{V_{\max }}{K_{\mathrm{m}}+C}\end{array}\right. $$
(16)

The model has five parameters (V max, K m, Cl d , V c, and V t) and three constants (two doses, one duration of infusion). We fit the data simultaneously.

The key features of this analysis are initially a bi-exponential concave decline after an intravenous constant rate infusion, followed by nonlinear capacity-dependent elimination that transgresses into a convex downward bend. The terminal portion of the curve displays a linear mono-exponential decline. The bi-exponential behavior suggests a two-compartment structure and the nonlinearity a Michaelis-Menten type of elimination. If we then apply the extended Eq. 1 with necessary parameters for the present dataset, we get Eq. 17

$$ \mathrm{N}\mathrm{P}=2\cdot \mathrm{EX}+\mathrm{N}\mathrm{L}=2\cdot 2+1=5 $$
(17)

which gives five parameters that are estimable from data (Cl d , V c, V t, V max, and K m).

Case study 9

Three oral doses of compound Y were given to the same subject at three different occasions. No lag time was observed but there was a peak shift in the plasma concentrations as the dose increased (Fig. 7, case study 9, red vertical lines (2)). The post-peak events become more and more shallow as dose increases. The three time courses fall off in a linear parallel fashion as concentrations approach less than 5–10 μg L−1. The pharmacokinetics may be characterized by a one-compartment model with first-order absorption and saturable elimination. The peak shift may be due to saturable absorption or saturable elimination. Provided complete absorption (100% bioavailability) or saturable absorption, the dose-normalized areas would superimpose. However, in this case study, the dose-normalized areas do not superimpose suggesting that nonlinear elimination causes the peak shift.

Fig. 7
figure 7

Case study 9 Semi-logarithmic plot of observed (solid symbols) and model-predicted (lines) concentration-time data in one subject after three different doses of test compound Y. F, K a, V, V max, and K m denote the bioavailability, absorption rate constant, volume of distribution, maximum metabolic rate, and Michaelis-Menten constant, respectively. Case study 10 Semi-logarithmic plot of observed (symbols) and model-predicted (lines) concentration-time data after oral dosing of a test compound that utilizes an endogenous transporter route. The oral profiles display nonlinear absorption with a peak shift in C max with increasing doses. A typical bi-phasic decline is shown post-peak and below plasma concentrations of approximately 100 μg L−1. Note the flip-flop situation during the first 120 min at the highest dose where rate of elimination is confounded by absorption. F, V max, K m, V c, V t, Cl d , and Cl denote bioavailability, maximum transport rate, the Michaelis-Menten constant related to the saturable absorption process, central volume, peripheral volume, inter-compartmental distribution, and clearance, respectively. Case study 11 Semi-logarithmic plot of concentration-time data obtained from a post-menopausal woman who received a rapid injection of 10 nmol of estradiol. An apparent bi-exponential decline approaches a baseline at approximately 20 pmol L−1. This behavior corresponds to a two-compartment system (right) with parallel endogenous (turnover, synthesis) and exogenous (intravenous bolus) input of estradiol. There is absolutely no need to subtract baseline values from experimental data in order to model the data. Cl, V c, V t, Cl d , and turnover rate denote clearance, central volume, peripheral volume, inter-compartmental distribution, bioavailability, and endogenous turnover rate, respectively. Case study 12 Observed (filled circles) and model-predicted (line) concentration-time data of growth hormone after a subcutaneous dose of 40 μg kg−1. The shaded area shows the area corresponding to exogenous input of growth hormone. Turnover, Cl, V, F, and K a denote the endogenous turnover rate, clearance, volume of distribution, bioavailability, and absorption rate constant, respectively. Data are displayed on a linear scale which more clearly highlights the key features.

Full size image

The equations corresponding to the concentration in plasma are written as

$$ \left\{\begin{array}{l}{\mathrm{Input}}_{\mathrm{po}}=F\cdot {K}_{\mathrm{a}}\cdot {\mathrm{Dose}}_i\cdot {e}^{-{K}_{\mathrm{a}}\cdot t}\\ {}\\ {}V\cdot \frac{dC}{dt}={\mathrm{Input}}_{\mathrm{po}}-{\mathrm{Cl}}_{\mathrm{MM}}\cdot C\\ {}\\ {}{\mathrm{Cl}}_{\mathrm{MM}}=\frac{V_{\max }}{K_{\mathrm{m}}+C}\end{array}\right. $$
(18)

The key features of this analysis are peak shifts with increasing oral doses with t max at 40, 50, and 100 min after the low, intermediate, and high doses, respectively. The peak concentration is followed by an apparent nonlinear and seemingly flatter portion of the curve at the highest dose. The terminal decline below 10 μg L−1 is mono-exponential. Dose-normalized areas do not superimpose which suggests either nonlinear bioavailability or nonlinear elimination. If we then apply the extended Eq. 1 with necessary parameters for the present dataset, we get

$$ \mathrm{N}\mathrm{P}=\mathrm{ABS}+2\cdot \mathrm{EX}+\mathrm{N}\mathrm{L}=1+2\cdot 1+1=4 $$
(19)

four parameters that are estimable from data (K a, V, V max, and K m).

Case study 10

Three oral solutions of a test compound with increasing doses to human subjects displayed a nonlinear pattern at the peak concentrations (Fig. 7, case study 10 (2)). The initial rise of the plasma concentration is very rapid with a peak concentration occurring within 10 min after dosing at the first observation. Not only was a peak shift observed with increasing doses but also a flat portion at the highest dose lasting for about 100 min. Dose-normalized areas, obtained from non-compartmental analysis, superimposed, suggesting that the extent of absorption is complete but the rate is saturable. The compound utilizes a transporter system for endogenous compounds like amino acids, hormones, and other food ingredients. Data also displays a bi-exponential (concave) decline at concentrations below 100 μg L−1. Figure 7 (case study 10) shows the high-resolution data from a single individual. The data pattern is interesting as it displays a brief period with absorption rate-limited kinetics during the first 100 min, and then displays disposition rate-limited kinetics in the terminal phase.

The function of the concentration in the central compartment is written as

$$ \left\{\begin{array}{l}\mathrm{In}=\frac{V_{\max}\cdot {A}_{\mathrm{g}}}{K_{\mathrm{m}}+{A}_{\mathrm{g}}}\\ {}\\ {}{V}_{\mathrm{c}}\cdot \frac{dC}{dt}=\mathrm{In}-\mathrm{C}\mathrm{l}\cdot C-{\mathrm{Cl}}_d\cdot C+{\mathrm{Cl}}_d\cdot {C}_{\mathrm{t}}\\ {}\\ {}{V}_{\mathrm{t}}\cdot \frac{d{C}_{\mathrm{t}}}{dt}={\mathrm{Cl}}_d\cdot C+{\mathrm{Cl}}_d\cdot {C}_{\mathrm{t}}\end{array}\right. $$
(20)

where V max, A g, and K m represent the maximum transport rate (μg min−1), amount in the gut compartment (μg), and the Michaelis-Menten constant (μg) at which half-maximal input rate operates. The model has five parameters (V max, K m, Cl d , V c, and V t) and three constants (three doses). The three concentration-time courses are fit simultaneously. It is the nonlinear input function in Eq. 20 that allows us to capture the nonlinear absorption pattern.

The key features of this analysis are an initial rapid rise in plasma concentrations with a peak within 10 min after dosing for the lowest dose followed by peak shifts in C max and an extended plateau at the highest dose. The time courses display bi-exponential decline at concentrations below 100 μg L−1. Dose-normalized areas-under-the plasma concentration curves superimpose suggesting complete absorption and linear elimination. If we then apply the extended Eq. 1 with necessary parameters for the present dataset, we get

$$ \mathrm{N}\mathrm{P}=\mathrm{ABS}+2\cdot \mathrm{EX}+\mathrm{N}\mathrm{L}=1+2\cdot 2+1=6 $$
(21)

However, there are only five parameters that are estimable from data (V max and K m, Cl d /F, V c/F, V t/F,). Since we apply a nonlinear transport to the absorption process, both ABS and NL relate to the same process.

Case study 11

Estradiol was given as a rapid intravenous injection to a post-menopausal woman. Estradiol concentrations in plasma were measured prior to dosing and during 32 h post-dosing (Fig. 7, case study 11 (2)). A two-compartment model with endogenous turnover and clearance was fit to the data. Initial parameters were obtained by graphical methods.

The bi-exponential decline observed in Fig. 7 (case study 11) displays two distinct phases before the estradiol plasma concentration asymptotically approaches the baseline concentration. The two phases are separated by a concave bend in the curve. The bi-exponential decline approaching a baseline can be described by a system of differential equations (Eq. 22). The relationship between the concentration C and the rate of change dC/dt in plasma and tissue can be expressed mathematically as a system of two differential equations for a two-compartment model with first-order kinetics, when drug is administered as a bolus dose as follows:

$$ \left\{\begin{array}{l}{V}_{\mathrm{c}}\cdot \frac{dC}{dt}={\mathrm{Input}}_{\mathrm{bolus}}+{R}_{\mathrm{in}}-\mathrm{C}\mathrm{l}\cdot C-{\mathrm{Cl}}_d\cdot C+{\mathrm{Cl}}_d\cdot {C}_{\mathrm{t}}\hfill \\ {}{V}_{\mathrm{t}}\cdot \frac{d{C}_{\mathrm{t}}}{dt}={\mathrm{Cl}}_d\cdot C-{\mathrm{Cl}}_d\cdot {C}_{\mathrm{t}}\hfill \end{array}\right. $$
(22)

dC/dt and dC t /dt are the rate of change of test compound in plasma and tissue, C is the plasma concentration, C t the tissue concentration, Cl plasma clearance, V c central volume, V t peripheral volume, and Cl d the inter-compartmental distribution parameter. Cl d has the units of volume per time (mL min−1 or L min−1) and is related to transport via blood flow, transporters, and diffusion/convection forces. Inputsc and R in denote the exogenous bolus dose and endogenous secretion of estradiol, respectively. R in is a model parameter that will be estimated together with Cl, Cl d , V c, and V t when fitting the model to the data. Here, we assume the endogenous production of estradiol is constant during the observational time period.

The key features of this analysis are bi-exponential decline in plasma, a baseline at 20 pmol L−1, and a short effective half-life. Baseline subtracted data would reveal an apparent bi-exponential decline. Extending the reasoning of Eq. 1, we would suggest that an additional parameter is needed in the model and that is the baseline information BL. Applying Eq. 1 with the baseline information included gives Eq. 23

$$ \mathrm{N}\mathrm{P}=2\cdot \mathrm{EX}+\mathrm{B}\mathrm{L}=2\cdot 2+1=5 $$
(23)

which corresponds to five parameters (R in, Cl, Cl d , V c, and V t) to be estimated.

Case study 12

This case study of pattern recognition demonstrates the turnover concept including turnover rate and turnover time. A healthy volunteer received a 40 μg kg−1 dose D of growth hormone subcutaneously (sc). The plasma concentrations of growth hormone, which were measured before and during 72 h post-dosing, are shown in Fig. 7 (case study 12 (2)) together with predicted concentrations. The data pattern includes a pre- and post-dose baseline concentration, a plasma concentration peak at about 2 h, and a rapid return back to baseline concentrations within 24 h.

The pre-dose concentration was 32 μg L−1. We will estimate the basic kinetic parameters such as clearance Cl/F (denoted Cl), volume of distribution V/F (denoted V), and absorption rate constant K a. The underlying differential equation that takes endogenous turnover rate R in and elimination Cl, together with the subcutaneous application, into account is

$$ \left\{\begin{array}{l}{\mathrm{In}}_{\mathrm{sc}}={K}_{\mathrm{a}}\cdot {\mathrm{FD}}_{\mathrm{sc}}\cdot {e}^{-{K}_{\mathrm{a}}\cdot t}\\ {}\\ {}V\cdot \frac{dC}{dt}={R}_{\mathrm{in}}+{\mathrm{In}}_{\mathrm{sc}}-\mathrm{C}\mathrm{l}\cdot C\end{array}\right. $$
(24)

We assume that the baseline concentration (initial condition) can be written as R in/Cl (synthesis or turnover rate divided by Cl), and that F is equal to unity.

The key features of this analysis are bi-exponential input/output, a baseline at 32 μg L−1, and a short effective half-life. Extending the reasoning of Eq. 1, we would suggest that an additional parameter be added to the model and that is baseline information BL. Applying Eq. 1 with the baseline information included gives Eq. 25

$$ \mathrm{N}\mathrm{P}=2\cdot \mathrm{EX}+\mathrm{ABS}+\mathrm{B}\mathrm{L}=2\cdot 1+1+1=4 $$
(25)

which corresponds to four parameters (R in, Cl/F, V/F, K a) to be estimated.

Case study 13

This case study covers the analysis of target-mediated disposition TMDD. Assuming high affinity of ligand to target, we provide a quantitative solution of ligand, soluble target, and ligand-target complex after a rapid intravenous injection dosing of the ligand. Data on the ligand concentration-time courses after four rapid intravenous injection doses are shown in Fig. 8 (case study 13 (2,7)).

Fig. 8
figure 8

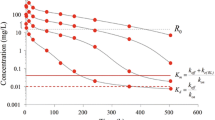
Case study 13 Semi-logarithmic plot of observed (symbols) and TMDD model-predicted concentrations (solid lines) at four different doses of 1.5, 5, 15, and 45 mg kg−1 after rapid intravenous injections of a monoclonal antibody. Note that the ligand displays a multi-compartment target-mediated disposition pattern that changes in shape with the change in ligand exposure (dose). The plot also shows the plasma target baseline concentration R 0, the estimated Michaelis-Menten constant K m, and the dissociation constant K d (7). Case study 14 Observed (filled circles) and predicted (solid line) plasma concentrations of nortriptyline (10 mg tid) before (A, 0–216 h), during (B, 216–516 h), and after (C, 516–700 h) pentobarbital Pb treatment. The horizontal bar represents the induction period. Data are displayed on a Cartesian scale due to the limited concentration range which more clearly highlights the key features. Case study 15 Observed (filled symbols) and model predictions (lines) of parent compound (solid lines) and metabolite (dashed lines) plasma concentration-time data. Note the change in half-life with increasing concentrations. The intravenous bolus doses of drug were 10, 50, and 300 μmol kg−1. The red solid lines are included as a visual help with respect to how the slope changes across low and high exposure data. Note the separation between parent C and metabolite C M concentrations with increasing doses of parent compound. C, V c, V t, Cl d , ClM, V max, K m, V M, and k ME denote the parent plasma concentration, central volume, peripheral volume, inter-compartmental distribution, metabolic clearance of parent compound, maximum metabolic capacity, the Michaelis-Menten constant, volume of distribution of metabolite, and elimination rate constant of metabolite, respectively. Case study 16 Observed (filled symbols) and model-predicted (lines) concentration-time data following an oral dose of 20 mg of compound A. The zero-order absorption model predicts a discontinuous line at approximately 4 h. The gray horizontal line illustrates the length of constant rate drug input T abs. The first-order model misses the peak concentration and displays systematic deviations between observed and model-predicted concentrations. Note the delayed absorption with a maximum observed plasma concentration at 4 h. K a, T abs, V (actually V/F), and K denote the absorption rate constant, duration of the zero-order absorption, volume of distribution, and elimination rate constant, respectively. Data are displayed on a Cartesian scale due to the limited concentration range which more clearly highlights the key features.

Full size image

The TMDD model is schematically depicted in Fig. 8 (case study 13). The typical shapes of a plasma concentration-time course that TMDD displays start with a rapid decline within the minute to hour range due to the second-order reaction between ligand and soluble target. This phase is extended in both the concentration and the time range with diminishing doses. Remember that the rate process –k on L R is dependent on both ligand and target concentrations and their relative sizes. The initial drop may easily be missed if the first plasma sample is 12–24 h post-dose. Then, the curve displays a concave bend towards a slower decline. One often has first-order linear (dose-proportional) kinetics at higher exposure of ligand. The concentration-time course displays bi-exponential decline at higher doses after intravenous dosing because the target, as a clearing route, is saturated.

The third typical phase is then a convex bend downward with a shorter apparent half-life as we approach lower concentrations. This phase is where TMDD starts to be of importance. The kinetics is now nonlinear. The appearance of the downward bend will occur at the same ligand concentrations independently of ligand dose. Throughout this phase, the target route of elimination is more or less saturable, but less saturable at low concentrations and therefore a more dominating clearing route in that concentration range.

Finally, the ligand enters a slower terminal phase, again after a concave bend, with a longer apparent half-life. This phase is very much governed by the elimination rate constant k e (RL) of complex RL and in some instances also by unspecific distribution (Cl d , V t) of ligand.

The disposition of the antibody (ligand, L) is described by a two-compartment non-specific disposition model coupled to a zero-order production first-order loss target pool R. Ligand and target forms a complex RL via a second-order process. The complex can either be degraded into ligand and target via the first-order k off process or be irreversibly lost via k e (RL) (first-order internalization or sink parameter). The combination of the second-order formation and first-order loss of complex makes the system nonlinear.

$$ \left\{\begin{array}{l}{V}_{\mathrm{c}}\cdot \frac{d{C}_L}{dt}={\mathrm{Input}}_{\mathrm{L}}-{\mathrm{Cl}}_{\mathrm{L}}\cdot {C}_{\mathrm{L}}-{\mathrm{Cl}}_d\cdot {C}_{\mathrm{L}}+{\mathrm{Cl}}_d\cdot {C}_{\mathrm{t}}\hfill \\ {}{V}_{\mathrm{t}}\cdot \frac{d{C}_t}{dt}={\mathrm{Cl}}_d\cdot {C}_{\mathrm{L}}-{\mathrm{Cl}}_d\cdot {C}_{\mathrm{t}}\hfill \\ {}\begin{array}{l}\frac{dR}{dt}={k}_{\mathrm{in}}-{k}_{\mathrm{out}}\cdot R-{k}_{\mathrm{on}}\cdot {C}_{\mathrm{L}}\cdot R+{k}_{\mathrm{off}}\cdot {C}_{\mathrm{RL}}\\ {}\frac{d{C}_{\mathrm{RL}}}{dt}={k}_{\mathrm{on}}\cdot {C}_{\mathrm{L}}\cdot R-{k}_{\mathrm{off}}\cdot {C}_{\mathrm{RL}}-{k}_{e\left(\mathrm{R}\mathrm{L}\right)}\cdot {C}_{\mathrm{RL}}\end{array}\hfill \end{array}\right. $$
(26)

C L, inputL, Cl L , Cl d , k on, R, k off, C RL, C T, and V t denote the ligand concentration, input of ligand, first-order clearance of ligand, inter-compartmental distribution of ligand, second-order rate constant for the ligand-target interaction, target level, first-order dissociation rate constant of the ligand-target complex, complex concentration, concentration of ligand in tissue due to non-specific distribution, and the volume of distribution of non-specific distribution of ligand. The k e(RL) is the first-order rate constant of irreversible removal of the complex.

It should also be remembered that the concentration-time courses similar to those following intermediate doses may in some instances also be observed for therapeutic proteins that do not undergo TMDD but exhibit the formation of clearing anti-drug antibodies (ADA) due to an immunological reaction (8). This usually takes some time to develop and is sometimes seen after repeated dose administration of, for example, monoclonal antibodies.

The number of parameters NP which may be calculated based on the observed pattern in Fig. 8 depends on the number of apparent exponentials EX (=3 apparent linear phases in the semi-logarithmic diagram) visible in the plasma concentration-time profile, the number of tissue spaces or binding proteins TS (=1 target) analyzed, and the number of visible nonlinear features NL (=1) in the data. This information results in

$$ \mathrm{N}\mathrm{P}=2\cdot \mathrm{EX}+2\cdot \mathrm{T}\mathrm{S}+\mathrm{N}\mathrm{L}=2\cdot 3+2\cdot 1+1=9 $$
(27)

This gives nine parameters based on the very simple relationship in Eq. 27. Still, additional concentration-time data on target (=2 parameters) and complex (=3 parameters) need to be included to improve the precision of certain parameters. See Peletier and Gabrielsson (7) for a thorough discussion of this dataset.

Case study 14

This case study illustrates how the time course of a drug can change upon repeated dosing when the enzymes responsible for its metabolism are induced. A study was conducted to see if the drug metabolizing enzymes of nortriptyline NT are inducible by pentobarbital PB by a hetero-induction process. NT was therefore administered orally as a 10-mg dose every 8 h for a period of 29 days (696 h). After 9 days (216 h), treatment with PB (inducer) was initiated and lasted for 12.5 days (300 h), i.e., until 21.5 days (516 h) after the start of NT administration. The observed and predicted plasma concentration-time course of NT before, during, and after treatment with inducer is depicted in Fig. 8 (case study 14 (9)).

$$ \left\{\begin{array}{l}V\cdot \frac{dC}{dt}={\mathrm{Input}}_{\mathrm{po}}-\mathrm{C}\mathrm{l}(t)\cdot C\hfill \\ {}{\mathrm{Input}}_{\mathrm{po}}={D}_{\mathrm{po}}\cdot {K}_{\mathrm{a}}\cdot {e}^{-{K}_{\mathrm{a}}\cdot t}\hfill \\ {}\mathrm{C}\mathrm{l}(t)={\mathrm{Cl}}_{\mathrm{induced}}-\left({\mathrm{Cl}}_{\mathrm{induced}}-{\mathrm{Cl}}_{\mathrm{uninduced}}\right)\cdot {e}^{-{k}_{\mathrm{out}}\cdot t}\hfill \end{array}\right. $$
(28)

where V, Cl(t), Inputpo, C, D po, K a, Clinduced, Cluninduced, and k out denote volume of distribution, time-dependent clearance of nortriptyline, nortriptyline plasma concentration, oral nortriptyline dose, absorption rate constant, induced clearance (from pentobarbital treatment), uninduced (pre-pentobarbital treatment) clearance, and fractional turnover rate of the inducible enzyme, respectively. Two hundred hours after the start of the study pentobarbital treatment was initiated (Fig. 8, case study 14, A). During induction, the half-life is continuously shortened (10 h) resulting in a reduced time to the induced steady state (Fig. 8, case study 14, B) in contrast to the return from the induced state (Fig. 8, case study 14, C) when Cl/F constantly diminishes and the corresponding half-life returns back to its pre-induction value. The exposure to nortriptyline is also more than halved during induction. Due to the constantly changing clearance (increasing) and half-life (decreasing), the time to steady state during the induction period is extended in spite of the fact that half-life is getting shorter (10 h) than before induction (25 h). The principle of three to four half-lives until steady state is not applicable for a system where half-life is constantly changing.

Case study 14 has demonstrated the consequences of induction of the responsible metabolizing enzymes by another compound (hetero-induction by pentobarbital on nortriptyline metabolism). Induction or inhibition by the parent compound itself or a metabolite is also possible (e.g., carbamazepine (10)). This is manifested as a lower (induction, causing the half-life to decrease) or higher (inhibition, causing the half-life to increase) exposure to the test compound over time. Saturable tissue binding can also lead to a lack of predictive power by single-dose data. It is therefore suggested that chronic indications require chronic dosing, and consequently pharmacokinetic assessment must be based on repeated dose information.

The key features of these patterns are steady-state exposure data after oral administration of nortriptyline which then diminishes by means of the induction process (through values and a complete time course peri-induction) and then shows a post-induction return towards pre-induction steady state. Applying Eq. 1 gives Eq. 29

$$ \mathrm{N}\mathrm{P}=2\cdot \mathrm{EX}+\mathrm{ABS}+\mathrm{N}\mathrm{L}=2\cdot 1+1+1=4 $$
(29)

which corresponds to four parameters (k out, Cl/F, V/F, K a) to be estimated.

Case study 15

The concentration of drug A and metabolite M were measured in plasma at different times after intravenous bolus doses of 10, 50, and 300 μmol kg−1. Figure 8 (case study 15 (2)) depicts the experimental concentration data for drug (solid lines) and metabolite (dashed lines).

The parent compound data show a bi-exponential decline with a concave curvature at about 30 min. The half-life of parent compound increases with increasing concentrations (doses). Notice that the metabolite peak concentration increases in a less than proportional manner and occurs later in time with increasing doses. The slope of the initial or intermediate portion of the plasma concentration-time profiles increases with dose and the separation of the parent and metabolite-time courses increases with higher doses. The terminal portion obeys first-order kinetics and should therefore be independent of dose (concentration). This pattern suggests a two-compartment system of differential equations for the parent compound (drug) with saturable elimination. The nonlinear elimination from parent becomes nonlinear formation input to a one-compartment metabolite (M) model. The three-compartment system is given by Eq. 30. In this model, an intravenously administered drug is fully converted to metabolite through its metabolic clearance and then excreted as the metabolite.

The system of differential equations of this model is

$$ \left\{\begin{array}{l}{V}_{\mathrm{c}}\cdot \frac{dC}{dt}=\mathrm{In}-{\mathrm{Cl}}_{\mathrm{M}}\cdot C-{\mathrm{Cl}}_d\cdot C+{\mathrm{Cl}}_d\cdot {C}_{\mathrm{t}}\\ {}{\mathrm{Cl}}_{\mathrm{M}}=\frac{V_{\max }}{K_{\mathrm{m}}+C}\\ {}{V}_{\mathrm{t}}\cdot \frac{d{C}_{\mathrm{t}}}{dt}={\mathrm{Cl}}_d\cdot C-{\mathrm{Cl}}_d\cdot {C}_{\mathrm{t}}\\ {}{V}_{\mathrm{M}}\cdot \frac{d{C}_{\mathrm{M}}}{dt}={\mathrm{Cl}}_{\mathrm{M}}\cdot C-{\mathrm{Cl}}_{\mathrm{M}\mathrm{E}}\cdot {C}_{\mathrm{M}}\end{array}\right. $$
(30)

The ClME parameter is the first-order clearance parameter of the metabolite. Note that ClM is the metabolic clearance of the drug, which is the same as the formation clearance of the metabolite. ClM will be more and more saturated, the higher the doses are of the parent compound. This results in formation-limited elimination of the metabolite and is observed as a flatter concentration-time course (longer apparent half-life of metabolite) at higher exposure to the parent compound.

The key features of this analysis are three bi-exponential time courses after intravenous dosing of parent compound. Data also contains information about the rise and fall of a metabolite in plasma which occurs via a saturable process. In this case, we have two different data sources which allow us to estimate

$$ \mathrm{N}\mathrm{P}=2\cdot \mathrm{EX}+\mathrm{N}\mathrm{L}+\mathrm{M}\mathrm{T}\mathrm{B}=2\cdot 2+1+2\cdot 1=7 $$
(31)

seven parameters (V max, K m, Cld, V c, V t, V ME, and ClME).

Case study 16

A volunteer was given 20 mg orally of a highly polar drug (Fig. 8, case study 16 (2)). Data show an initial time delay followed by a late peak at about 4 h and a post-peak mono-exponential decline. The objectives of this exercise are therefore to identify and fit the most suitable of two different types of absorption models to a dataset obtained after extravascular dosing with compound A. One is a first-order model including a lag time, the other is a zero-order input model.

The absorption process from the gastrointestinal tract is complex and involves several processes such as disintegration of the tablet, dissolution of the drug into the gastric fluids, gastric emptying, diffusion across the gut wall to mention just a few. In general, absorption processes are assumed to occur by means of a first-order process, although there are exceptions. Under certain conditions, it has been found that absorption of compounds is better described by zero-order kinetics. The first- and zero-order input models are shown in Eq. 32.

$$ \left\{\begin{array}{l}V\cdot \frac{dC}{dt}=\mathrm{Input}\ \mathrm{r}\mathrm{ate}-\frac{\mathrm{Cl}}{F}\cdot C\hfill \\ {}\mathrm{First}\hbox{-} \mathrm{order}\ \mathrm{input}\ \mathrm{r}\mathrm{ate}=\left\{\begin{array}{l}=0\kern0.5em \mathrm{when}\kern0.5em t<{t}_{\mathrm{lag}}\\ {}\mathrm{else}\\ {}={K}_{\mathrm{a}}\cdot {D}_{\mathrm{po}}\cdot {e}^{-{K}_{\mathrm{a}}\cdot \left(t-{t}_{\mathrm{lag}}\right)}\end{array}\right.\hfill \\ {}Z\mathrm{e}\mathrm{r}\mathrm{o}\hbox{-} \mathrm{order}\ \mathrm{input}\ \mathrm{r}\mathrm{ate}\kern0.5em \left\{\begin{array}{l}=\frac{D_{\mathrm{po}}}{T_{\mathrm{a}\mathrm{bs}}}\ \mathrm{when}\ t<{T}_{\mathrm{a}\mathrm{bs}}\\ {}\mathrm{else}\\ {}=0\end{array}\right.\hfill \end{array}\right. $$
(32)

where T abs is the assumed duration of zero-order input. Equation 31 is equivalent to a one-compartment continuous infusion model where the duration of the infusion T abs is estimated as a parameter.

In this case study, there is a distinct difference between the zero-order input (model of choice) and first-order input models (systematic deviations throughout the model-predicted concentration-time course), which is already shown in the function plots. In other words, the latter model is not an option and there is no need to extend the analysis to inspection of residuals or use other tools in the statistical battery (parameter precision, correlation, F test) (see Gabrielsson and Weiner (2) for a discussion).

The key pattern of this dataset is a somewhat delayed onset of absorption, a concentration maximum at about 4 h, and a mono-exponential decline post-peak.

Applying Eq. 1 gives Eq. 33

$$ \mathrm{N}\mathrm{P}=2\cdot \mathrm{EX}+\mathrm{ABS}+\mathrm{T}\mathrm{L}\mathrm{G}=2\cdot 1+1+1=4 $$
(33)

which corresponds to four parameters (t lag or T abs and Cl/F, V/F, K a) to be estimated.

DISCUSSION

Pattern recognition is a pivotal aspect of exploratory data analysis when modeling pharmacokinetic and pharmacodynamic data. Therefore, a rigorous strategy is essential for dissecting the patterns that concentration-time profiles reveal. As an alternative solution, one may utilize a set of points to consider that specifically addresses number of phases, convex or concave bending, time lags, peak shifts, baseline behavior, effective half-lives, dose-normalized areas, concentration plateaus, and similar phenomena. Pattern recognition has also been proposed for interpreting results of drug-drug interactions. “A quicker and better understanding about the processes, which dominate a DDI, has been achieved using this approach by focusing on integration of all information available and mechanistic interpretation” (1).

The application of the extended Eq. 1 has been successful for the presented case studies but should in general be used cautiously and only from an exploratory point of view. One may decipher other characteristics of the data by for example simultaneously fitting several time courses.

Considerations and Methodologies for Comparison and Experimental Design

We advocate an iterative process for discrimination between rival models. This is done by starting with a simpler model (say bi-exponential or no lag time model), fit that model to the data, perform a thorough residual analysis (2), and look at other goodness-of-fit criteria (objective function value, Akaike information criteria, etc.) together with parameter correlation and precision. The next step is then to systematically extend the model (adding an exponential term or a lag time if necessary), refit the updated model to the data, and inspect the residuals in combination with the statistical battery (goodness-of-fit, parameter precision, parameter correlation). In some cases, an F test analysis may be a final check of the model of choice, although the residual analysis (again visual inspection of transformed data) is, in our experience, a powerful approach in model selection. The most parsimonious model is preferable in most modeling situations.

We advocate an iterative approach to practical experimental design. Start by running a pilot study with a single dose, a few animals, and logarithmic spacing of data in time. Then fit a model to the data to get an acceptable fit as possible without overdoing the analysis. Simulate the new design(s) with the model using the final parameter estimates from the pilot study. Propose alternative doses, alternative sampling time points, and/or a repeated dose design if necessary. Run the study and collect data according to revised design. Now fit all data from pilot and redesigned study simultaneously. If the model mimics all data, it is probably a relatively robust model. We commonly use this iterative approach (running a dose-range finding limited animal/sample approach) prior to the more expensive repeated dose (e.g., 1-, 3-, or 12-month safety) studies. There are several real-life case studies in Gabrielsson and Weiner where simultaneous fitting of data from two or more (incomplete) experiments have proven to be useful (2). One may also want to consider sparse sampling in combination with a mixed-effects modeling approach to save both animals and cost. The mixed-effects modeling approach has of course great potential but is beyond the focus of this report.

Some General Points to Consider with Respect to Visual Inspection of Data

Data collected from intravenous dosing are used for assessment of the disposition (binding, distribution, elimination) of a test compound in plasma and urine. Central themes of what one observes in data patterns are the following:

  1. (1)

    the number of exponential phases in a semi-logarithmic concentration-time plot corresponds to the number of compartments in a linear mammillary compartment system after a rapid bolus injection or a short constant intravenous infusion.

    $$ \mathrm{Number}\ \mathrm{of}\ \mathrm{compartments}=\mathrm{Number}\ \mathrm{of}\ \mathrm{phases}\ \mathrm{in}\ \mathrm{plasma} $$
    (35)
  2. (2)

    Nonlinearities such as capacity-, time-, binding-, and flow-dependent phenomena (Eq. 36) are revealed by convex bends in the concentration-time profile (see case studies 7–9, 13, and 15), which suggest that one or more nonlinear terms are needed in the model. Also, dose normalize the concentration-time curves and check whether they superimpose. A set of nonlinear expressions are collated below.

    $$ \mathrm{Nonlinearities}=\left\{\begin{array}{l}\mathrm{C}\mathrm{apacity}\kern0.5em \mathrm{C}\mathrm{l}=\frac{V_{\max }}{K_{\mathrm{m}}+C}\\ {}\mathrm{Time}\kern0.5em \mathrm{C}\mathrm{l}(t)=\frac{V_{\max }(t)}{K_{\mathrm{m}}+C}\\ {}\mathrm{Binding}\kern0.75em {f}_u=\frac{C_{\mathrm{u}}+{K}_d}{C_{\mathrm{u}}+{K}_d+n\cdot \left[{P}_T\right]}\\ {}\\ {}\mathrm{Flow}\kern0.75em \mathrm{C}\mathrm{l}=\frac{Q_{\mathrm{H}}\cdot {f}_u\cdot {\mathrm{Cl}}_{\mathrm{int}}}{Q_{\mathrm{H}}+{f}_u\cdot {\mathrm{Cl}}_{\mathrm{int}}}\\ {}\\ {}{\mathrm{Cl}}_{\mathrm{H}}=\frac{Q_{\mathrm{H},\mathrm{B}}\cdot {f}_u\cdot {{\mathrm{Cl}}_{\mathrm{u}}}_{\mathrm{int},\mathrm{H}}}{Q_{\mathrm{H},\mathrm{B}}+{f}_u\cdot {{\mathrm{Cl}}_{\mathrm{u}}}_{\mathrm{int},\mathrm{H}}/\left(\frac{C_{\mathrm{B}}}{C_{\mathrm{P}}}\right)}\end{array}\right. $$
    (36)

    V max(t), K d, n, [P T ], Q H, and Clint denote the time-dependent maximum metabolic capacity, affinity constant between drug and protein, number of binding sites on the protein, protein concentration, hepatic blood flow, and intrinsic clearance, respectively. ClH, Q H,B, f u, Clu int,H, C B, and C p are the hepatic blood clearance, hepatic blood flow, free fraction in plasma, unbound hepatic intrinsic clearance, total blood concentration, and total plasma concentration, respectively (11).

  3. (3)

    Extravascular data (oral data or data from alternative extravascular dosing) reveal time delays (t lag), rate (K a), and extent (F) of absorption, or even capacity-limited (V max, K m) input that impacts the onset of absorption, absorption rate, the AUC, and peak shifts in C max /t max when two or more doses are given, respectively. Useful expressions related to absorption profiles are shown in Eq. 37.

    $$ \mathrm{Absorption}=\left\{\begin{array}{l}\mathrm{Input}\ \mathrm{rate}\kern0.5em F\cdot {\mathrm{Dose}}_{\mathrm{po}}\cdot {e}^{-{K}_{\mathrm{a}}\cdot \left(t-{t}_{\mathrm{lag}}\right)}\hfill \\ {}\mathrm{Extent}\kern0.5em F={f}_{\mathrm{a}}\cdot {f}_{\mathrm{H}}\hfill \\ {}\mathrm{Capacity}\kern0.5em \mathrm{input}\ \mathrm{rate}=\frac{V_{\max }}{K_{\mathrm{m}}+{A}_{\mathrm{g}}}\hfill \end{array}\right. $$
    (37)

    A g , f a , and f H denote the amount at the absorption site (e.g., in the gut), fraction absorbed into blood, and fraction that passes through the liver, respectively. All other parameters are explained above. One should remember, however, that data from only the oral route may confound the interpretation of slopes, clearance, and volume terms. A potential solution to this is to utilize iv and oral data simultaneously.

  4. (4)

    Baseline concentrations of endogenous compounds need to be considered by adding some production term (turnover rate) simultaneously with the clearance parameter

    $$ \mathrm{Baseline}=\frac{\mathrm{Turnover}\ \mathrm{rate}}{\mathrm{Cl}} $$
    (38)

    When baseline values are observed for exogenous compounds one does not have to consider an endogenous turnover rate but rather setting the initial condition of the state variable(s) to the measured pre-dose value.

  5. (5)

    Measurements in other body tissues and fluids, for example, urinary data, may contribute to the estimation of either renal clearance ClR or fraction excreted via urine f e

    $$ \frac{d{A}_{\mathrm{u}}}{dt}={\mathrm{Cl}}_{\mathrm{R}}\cdot C={f}_{\mathrm{e}}\cdot \mathrm{C}\mathrm{l}\cdot C $$
    (39)

    where dA u /dt and C are the rate of excretion of drug into urine and the plasma concentration.

The objective of this communication has been to focus on visual inspection of “shapes” of concentration-time profiles in the exploratory analysis of pharmacokinetic data. We have tried to decompose the shapes and to systematically interpret what determines the rise, intensity, and decline of exposure. This approach may serve as a road map to pattern recognition of concentration-time data.

Additional sources of data from two or more doses, urine, metabolite information, and repeated dose data should, whenever possible, be considered as part of a simultaneous fitting procedure.