Skip to main content
SpringerLink
Log in

Bayesian spatial modeling of data from avian point count surveys

  • Published:
Journal of Agricultural, Biological, and Environmental Statistics Aims and scope Submit manuscript

Abstract

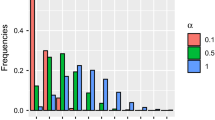
We present a unified framework for modeling bird survey data collected at spatially replicated survey sites in the form of repeated counts or detection history counts, through which we model spatial dependence in bird density and variation in detection probabilities due to changes in covariates across the landscape. The models have a complex hierarchical structure that makes them suited to Bayesian analysis using Markov chain Monte Carlo (MCMC) algorithms. For computational efficiency, we use a form of conditional autogressive model for modeling spatial dependence. We apply the models to survey data for two bird species in the Great Smoky Mountains National Park. The algorithms converge well for the more abundant and easily detected of the two species, but some simplification of the spatial model is required for convergence for the second species. We show how these methods lead to maps of estimated relative density which are an improvement over those that would follow from past approaches that ignored spatial dependence. This work also highlights the importance of good survey design for bird species mapping studies.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Similar content being viewed by others

References

  • Alho, J. M. (1990), “Logistic Regression in Capture-Recapture Models,” Biometrics, 46, 639–649.

    Article  MathSciNet  Google Scholar 

  • Alldredge, M. W., Pollock, K. H., Simons, T. R., Collazo, J. A., and Shriner, S. (2007), “Time of Detection Method for Estimating Abundance from Point Count Surveys,” The Auk, 124, 653–664.

    Article  Google Scholar 

  • Alsop, F. J. (1991), Birds of the Smokies, Gatlinburg, TN: Great Smoky Mountains Natural History Association.

    Google Scholar 

  • Banerjee, S., Carlin, B. P., and Gelfand, A. E. (2004), Hierarchical Modeling and Analysis for Spatial Data, Boca Raton, FL: Chapman and Hall.

    MATH  Google Scholar 

  • Besag, J. (1974), “Spatial Interaction and the Statistical Analysis of Lattice Systems,” Journal of the Royal Statistical Society, Series B, 36, 192–236.

    MATH  MathSciNet  Google Scholar 

  • Coull, B. A., and Agresti, A. (1999), “The Use of Mixed-Logit Models to Reflect Heterogeneity in Capture-Recapture Studies,” Biometrics, 55, 294–301.

    Article  MATH  Google Scholar 

  • Cressie, N. (1993), Statistics for Spatial Data (2nd ed.), New York: Wiley.

    Google Scholar 

  • Diggle, P. J., Tawn, J. A., and Moyeed, R. A. (1998), “Model-Based Geostatistics” (with discussion), Applied Statistics, 47, 299–350.

    MATH  MathSciNet  Google Scholar 

  • Dorazio, R. M., Jelks, H. L., and Jordan, F. (2005), “Improving Removal-Based Estimates of Abundance by Sampling a Population of Spatially Distinct Subpopulations,” Biometrics, 61, 1093–1101.

    Article  MathSciNet  Google Scholar 

  • Dorazio, R. M., and Royle, J. A. (2003), “Mixture Models for Estimating the Size of a Closed Population When Capture Rates vary Among Individuals,” Biometrics, 59, 351–364.

    Article  MathSciNet  Google Scholar 

  • Farnsworth, G. L., Pollock, K. H., Nichols, J. D., Simons, T. R., Hines, J. E., and Sauer, J. R. (2002), “A Removal Model for Estimating Detection Probabilities From Point-Count Surveys,” The Auk, 119, 414–425.

    Article  Google Scholar 

  • Forsyth, D. M., Link, W. A., Webster, R., Nugent, G., and Warburton, B. (2005), “Nonlinearity and Seasonal Bias in an Index of Brushtail Possum Abundance,” Journal of Wildlife Management, 69, 976–984.

    Article  Google Scholar 

  • Gelfand, A. E., and Vounatsou, P. (2003), “Proper Multivariate Conditional Autoregressive Models for Spatial Data Analysis,” Biostatistics, 4, 11–25.

    Article  MATH  Google Scholar 

  • Gelman, A. (2006), “Prior Distributions for Variance Parameters in Hierarchical Models” (comment on article by Browne and Draper), Bayesian Analysis, 1, 515–534.

    Article  MathSciNet  Google Scholar 

  • Gelman, A., Carlin, J. B., Stern, H. S., and Rubin, D. B. (2004), Bayesian Data Analysis (2nd ed.), Boca Raton, FL: Chapman and Hall.

    MATH  Google Scholar 

  • Geman, S., and Geman, D. (1984), “Stochastic Relaxation, Gibbs Distributions and the Bayesian Resolution of Images,” IEEE Transactions on Pattern Analysis and Machine Intelligence, 6, 721–741.

    Article  MATH  Google Scholar 

  • Hastings, W. K. (1970), “Monte Carlo Sampling Methods using Markov Chains and their Applications,” Biometrika, 57, 97–109.

    Article  MATH  Google Scholar 

  • Holzmann, H., Munk, A., and Zucchini, W. (2006), “On Identifiability in Capture-Recapture Models,” Biometrics, 62, 934–936.

    Article  MathSciNet  Google Scholar 

  • Hrafnkelsson, B., and Cressie, N. (2003), “Hierarchical Modeling of Count Data with Application to Nuclear Fall-Out,” Environmental and Ecological Statistics, 10, 179–200.

    Article  MathSciNet  Google Scholar 

  • Huggins, R. M. (1989), “On the Statistical Analysis of Capture Experiments,” Biometrika, 76, 133–140.

    Article  MATH  MathSciNet  Google Scholar 

  • Lichstein, J. W., Simons, T. R., Shriner, S. A., and Franzreb, K. E. (2002), “Spatial Autocorrelation and Autoregressive Models in Ecology,” Ecological Monographs, 72, 445–463.

    Article  Google Scholar 

  • Link, W. A. (2003), “Nonidentifiability of Population Size from Capture-Recapture Data with Heterogeneous Detection Probabilities,” Biometrics, 59, 1123–1130.

    Article  MATH  MathSciNet  Google Scholar 

  • McShea, W. J., and Rappole, J. H. (1997), “Variable Song Rates in Three Species of Passerines and Implications for Estimating Bird Populations,” Journal of Field Ornithology, 68, 367–375.

    Google Scholar 

  • Norris, J. L., and Pollock, K. H. (1996), “Nonparametric MLE Under Two Closed Capture-Recapture Models with Heterogeneity,” Biometrics, 52, 639–649.

    Article  MATH  Google Scholar 

  • Otis, D. L., Burnham, K. P., White, G. C., and Anderson, D. R. (1978), “Statistical Inference from Capture Data on Closed Animal Experiments,” Wildlife Monographs, 62, 1–135.

    Google Scholar 

  • Pinder, J. E., Kroh, G. C., White, J. D., and Basham May, A. M. (1997), “The Relationships Between Vegetation Type and Topography in Lassen Volcanic National Park,” Plant Ecology, 131, 17–29.

    Article  Google Scholar 

  • Pledger, S. (2000), “Unified Maximum Likelihood Estimates for Closed Capture-Recapture Models Using Mixtures,” Biometrics, 56, 434–442.

    Article  MATH  Google Scholar 

  • — (2005), “The Performance of Mixture Models in Heterogeneous Closed Population Capture-Recapture,” Biometrics, 61, 868–873.

    Article  MathSciNet  Google Scholar 

  • Pollock, K. H., Nichols, J. D., Brownie, C., and Hines, J. E. (1990), “Statistical Inference for Capture-Recapture Experiments,” Wildlife Monographs, 107.

  • Ralph, J. C., Droege, S., and Sauer, J. R. (1995), “Managing and Monitoring Birds Using Point Counts: Standards and Applications,” in Monitoring Bird Populations by Point Counts, eds., J. C. Ralph, J. R. Sauer, and S. Droege, U.S. Forest Service General Technical Report PSW-GTR-149, pp. 161–168.

  • Royle, J. A. (2004), “N-mixture Models for Estimating Population Size from Spatially Replicated Counts,” Biometrics, 60, 108–115.

    Article  MATH  MathSciNet  Google Scholar 

  • Royle, J. A., and Dorazio, R. M. (2006), “Hierarchical Models of Animal Abundance and Occurrence,” Journal of Agricultural, Biological, and Environmental Statistics, 11, 249–263.

    Article  Google Scholar 

  • Royle, J. A., Link, W. A., and Sauer, J. R. (2002), “Statistical Mapping of Count Survey Data,” in Predicting Species Occurences: Issues of Accuracy and Scale, eds. J. M. Scott, P. J. Heglund, M. L. Morrison, J. B. Haufler, M. G. Raphael, W. A. Wall, and F. B. Samson, Washington: Island Press.

    Google Scholar 

  • Seber, G. A. F. (1982), The Estimation of Animal Abundance and Related Parameters (2nd ed.), New York: Macmillan.

    Google Scholar 

  • Shriner, S. A. (2001), “Distribution of Breeding Birds in Great Smoky Mountains National Park,” unpublished PhD thesis, North Carolina State University.

  • Shriner, S. A., Simons, T. R., and Farnsworth, G. L. (2002), “A GIS-based Habitat Model for Wood Thrush, hylocichla mustelina, in Great Smoky Mountains National Park,” in Predicting Species Occurences: Issues of Accuracy and Scale, eds. J. M. Scott, P. J. Heglund, M. L. Morrison, J. B. Haufler, M. G. Raphael, W. A. Wall, and F. B. Samson, Washington: Island Press.

    Google Scholar 

  • Simons, T. R., Alldredge, M. W., Pollock, K. H., and Wettroth, J.M. (2007), “Experimental Analysis of the Auditory Detection Process on Avian Point Counts,” The Auk, 124, 986–999.

    Article  Google Scholar 

  • Simons, T. R., Farnsworth, G. L., and Shriner, S. A. (2000), “Evaluating Great Smoky Mountains National Park as a Population Source for the Wood Thrush,” Conservation Biology, 14, 1133–1144.

    Article  Google Scholar 

  • Simons, T. R., Shriner, S. A., and Farnsworth, G. L. (2006), “Comparison of Breeding Bird and Vegetation Communities in Primary and Secondary Forests of Great Smoky Mountains National Park,” Biological Conservation, 129, 302–311.

    Article  Google Scholar 

  • Spiegelhalter, D., Thomas, A., Best, N., and Lunn, D. (2003), WinBUGS User Manual, Version 1.4.

  • Thomas, A., Best, N., Lunn, D., Arnold, R., and Spiegelhalter, D. (2004), GeoBUGS User Manual, Version 1.2 September 2004.

  • Wikle, C. (2002), “Spatial Modelling of Count Data: A Case Study in Modelling Breeding Bird Survey Data on Large Spatial Domains,” in Spatial Chester Modelling, eds. A. B. Lawson, and G. T. Denison, Boca Raton: Chapman and Hall/CRC.

    Google Scholar 

  • Wyatt, R. J. (2002), “Estimating Riverine Fish Population Size from Single-and Multiple-Pass Removal Sampling using a Hierarchical Model,” Canadian Journal of Fisheries and Aquatic Science, 59, 695–706.

    Article  Google Scholar 

  • Zippen, C. (1956), “An Evaluation of the Removal Method of Estimating Animal Population,” Biometrics, 12, 163–189.

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. International Pacific Halibut Commission, 98145-2009, Seattle, WA

    Raymond A. Webster (Biometrician)

  2. Department of Zoology, North Carolina State University, 27695-7617, Raleigh, NC

    Kenneth H. Pollock (Professor)

  3. USGS, NC Cooperative Fish and Wildlife Research Unit, Department of Zoology, North Carolina State University, 27695-7617, Raleigh, NC

    Theodore R. Simons (Professor)

Authors
  1. Raymond A. Webster
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Kenneth H. Pollock
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Theodore R. Simons
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Raymond A. Webster.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Webster, R.A., Pollock, K.H. & Simons, T.R. Bayesian spatial modeling of data from avian point count surveys. JABES 13, 121–139 (2008). https://doi.org/10.1198/108571108X311563

Download citation

  • Received:

  • Revised:

  • Issue Date:

  • DOI: https://doi.org/10.1198/108571108X311563

Key Words

Search

Navigation