Abstract
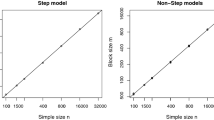
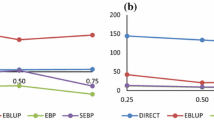
In environmental and agricultural studies, it is often of interestto compare spatial variables across different regions. Traditional statistical tools that assume independent samples are inadequate because of potential spatial correlations. In this article, spatial dependence is accounted for by a random field model, and a non parametric test is developed to compare the overall distributions of variables in two neighboring regions. Sampling distribution of the test statistic is estimated by a spatial block bootstrap. For illustration, the procedure is applied to study root-lesion nematode populations on a production farm in Wisconsin. Choices of the bootstrap block size are investigated via a simulation study and results of the test are compared to traditional approaches.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Bühlmann, P. (1994), “Blockwise Bootstrapped Empirical Process for Stationary Sequences,” The Annals of Statistics, 22, 995–1012.
Conover, W. J. (1999), Practical Nonparametric Statistics (3rd ed.), New York: Wiley.
Doukhan, P. (1994), Mixing: Properties and Examples, New York: Springer.
Künsch, H. R. (1989), “The Jackknife and the Bootstrap for General Stationary Observations,” The Annals of Statistics, 17, 1217–1241.
Lahiri, S. N., Kaiser, M. S., Cressie, N. and Hsu, N. J. (1999), “Prediction of Spatial Cumulative Distribution Functions Using Subsampling” (with discussion), Journal of the American Statistical Association, 94, 86–110.
Liu, R., and Singh, K. (1992), “Moving Blocks Jackknife and Bootstrap Capture Weak Convergence,” in Exploring the Limits of Bootstrap, eds. R. Lepage and L. Billard, New York: Wiley, pp. 225–248.
Morgan, G. D., MacGuidwin, A. E., Zhu, J., and Binning, L. K. (2002), “Population Dynamics of Root Lesion Nematode Over a Three-Year Potato Crop Rotation,” Agronomy Journal, 94, 1146–1155.
Olthof, Th. H. A. (1987), “Effects of Fumigants and Systemic Pesticides on Pratylenchus penetrans and Potato Yield,” Journal of Nematology, 19, 424–430.
Townshend, J. L., Potter, J. W., and Willis, C. B. (1978), “Ranges of Distribution of Species of Pratylenchus in Northeastern North America,” Canadian Plant Disease Survey, 58, 80–82.
Webster, R., and Oliver, M. (2001), Geostatistics for Environmental Scientists, New York: Wiley.
Zhu, J., and Lahiri, S. N. (2002), “Weak Convergence of Block wise Bootstrapped Empirical Process for Stationary Random Fields With Statistical Applications,” Technical Report 1070, Department of Statistics, University of Wisconsin-Madison.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Zhu, J., Morgan, G.D. Comparison of spatial variables over subregions using a block bootstrap. JABES 9, 91–104 (2004). https://doi.org/10.1198/1085711043154
Received:
Revised:
Issue Date:
DOI: https://doi.org/10.1198/1085711043154