Periodic review inventory model for Gumbel deteriorating items when demand follows Pareto distribution

Abstract

For the importance of deteriorating in units, this paper presents a Constraint Deteriorating Probabilistic Periodic Review Inventory Model (CDPPRIM), a model which is applicable under some assumptions: (1) the demand is a random variable that follows Pareto distribution without lead time, (2) some costs are varying and shortage is permitted, (3) the deterioration rate follows Gumbel distribution, and (4) there is a constraint on varying deteriorating cost.

Here, the objective function under a constraint is imposed in crisp and fuzzy environment. A Newton’s method is used to solve the system of nonlinear equations. The objective is to find the optimal values of four decision variables (maximum inventory level, stock-out time, the deteriorating time, and review time), which minimize the expected annual total cost under the assumptions. Finally, the model is followed by an application.

Introduction

Many researchers studied inventory models whether deterministic or probabilistic, single-item or multi-item. Some of them investigate a probabilistic periodic review inventory model. For example, Sqren and Roger [1] developed the model with continuous demand and lost sales. Iida [2] studied a non-stationary model with uncertain production capacity and uncertain demand. Chiang [3] presented optimal replenishment for the model with two supply modes. Fergany [4] developed the model with zero lead time under constraints and varying ordering cost using Lagrange multiplier technique. Abuo-El-Ata et al. [5] illustrated the model for multi-item with varying order cost under two restrictions using geometric programming approach.

The cost parameters in real inventory systems and other parameters such as price, marketing, and service elasticity of demand are imprecise and uncertain in nature. This uncertainty applied the notion of fuzziness. Since the proposed model is in a fuzzy environment, a fuzzy decision should be made to meet the decision criteria, and the results should be fuzzy. Many researchers introduced fuzzy sets and its application as a mathematical way of representing impreciseness or vagueness in everyday life. Dubois and Prade [6] presented a theory and application for fuzzy sets and system. Dey and Chakraborty [7] introduced fuzzy periodic review system with fuzzy random variable demand.

Deterioration plays a significant role in many inventory systems. Moreover, it is the one of main problems investigated in the inventory systems science more than 20 years ago. Because of this importance, many researchers have attempted to present models and applications that deal with this crucial point. For example, Azizul et al. [8] studied inventory model with Gumbel deteriorating items. Chern et al. [9] explained an inventory models for deteriorating items with fluctuating and inflation demand with partial backorder shortage. Taleizadeh and Nematollahi [10] presented a deterministic inventory control problem for deteriorating items with backordering and financial considerations. Priya et al. [11] introduced an inventory model for deteriorating items with exponential demand and time-varying holding cost. Maragatham and Lakshmidevi [12] explained an inventory model for non-instantaneous deteriorating items under conditions of permissible delay in payments for N cycles. Mishra et al. [13] introduced an inventory model for deteriorating items with time-dependent demand and time-varying holding cost under partial backorder.

This paper presents a new deteriorating probabilistic periodic review inventory model under a varying deterioration cost constraint. This model is applicable when the lead time is zero and when the demand is a random variable that follows Pareto distribution. It is also applicable when the shortage is allowed, and it is divided into backorders or/and lost sales. The paper studies that in Constraint Deteriorating Probabilistic Periodic Review Inventory Model (CDPPRIM) when the deterioration rate follows Gumbel distribution, some costs are varying, and the model works effectively in both crisp and fuzzy environments. The model solved through Lagrange multiplier technique. A numerical analysis method (Newton’s method) is used for solving nonlinear equations. The objective of this study is to find the optimal values of four decision variables (maximum inventory level, stock-out time, deteriorating time, and the review time), which minimize the expected annual total cost under a restriction. The results are acquired by using Mathematica program.

The following assumptions are made in developing the model:

• The replenishment rate is instantaneous (the lead time is zero).

• The deterioration rate θ(t) follows decreasing distributions as Gumbel distribution.

• The salvage value γ, 0< γ < 1 is associated to deteriorated units during the cycle.

• Shortage is allowed to occur, and it is a mixture of backorder and lost sales. A fraction ρ (0 ≤ ρ ≤ 1) is backordered. Then the remaining fraction (1 – ρ) is lost, $\rho =\frac{1}{1+\epsilon \left(N-t\right)},$ (0 < ϵ < 1).

• Suppose that the demand for a particular item follows Pareto distribution such as:

$f(x)=\frac{\eta\ {\delta}^{\eta }}{{\left(x+\delta \right)}^{\eta +1}},0\le x<+\infty, \kern1em \eta$ is a continuous shape parameter η > 0, δ is a continuous scale parameter δ > 0.

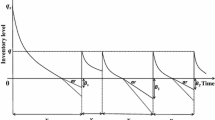
The model under consideration developed the stock level, which decreases at a uniform rate over the cycle as shown in Fig. 1.

Fig. 1

Inventory process for DPPRIM with mixture shortage

Mathematical model

In the interval (0, N), the inventory level gradually decreases to meet demands. During the period [0, n_d], the inventory depletes due to the demand. In addition, during the period [n_d, n₁], the inventory depletes due to the demand and deteriorating. By this process, during the interval [n₁, N], the inventory level reaches zero level at time n₁ and then shortage is allowed to occur. The probability density function of Gumbel distribution is $f(t)=\frac{1}{\sigma }{e}^{{\left\{\frac{\left(t-\mu \right)}{\sigma}\right\}}^{\xi +1}}{e}^{-{e}^{{\left\{\frac{\left(t-\mu \right)}{\sigma}\right\}}^{\xi +1}}},t>0$, where μ ∈ R is a location parameter, σ ∈ (0, ∞) is the scale parameter, and ξ ∈ (−∞, ∞) is the shape parameter. The shape parameter ξ governs the tail behavior of the distribution. The family defined by ξ → 0 corresponds to the Gumbel distribution. The probability density function of Gumbel distribution corresponds to minimum value ${f}_{\mathrm{min}}(t)=\frac{1}{\sigma }{e}^{\frac{\left(t-\mu \right)}{\sigma }}\ \mathrm{Exp}\left[-\mathrm{Exp}\left[\frac{\left(t-\mu \right)}{\sigma}\right]\right],t>0$. And the cumulative distribution function ${F}_{\mathrm{min}}(t)=1-\mathrm{Exp}\left[-\mathrm{Exp}\left[\frac{\left(t-\mu \right)}{\sigma}\right]\right],t>0.$

Then the deterioration rate function defined by ${\theta}_{min}(t)=\frac{1}{\sigma }{e}^{\frac{\left(t-\mu \right)}{\sigma }},t>0.$

The boundary conditions ${q}_1(0)={Q}_m,{q}_2\left({n}_1\right)={q}_3\left({n}_1\right)=0,{q}_3(N)=\overline{x}-{Q}_m$.

The differential equations for the instantaneous inventory level q_i (t), 0 < t < N are given by Eqs. (1), (2), (5), and (6).

• If x≤ Q_m, the rate of change of inventory during positive stock period [0, n₁] is governed by the following differential equations:

$$ \frac{d\ {q}_1(t)}{dt}=-\overline{D}=-\frac{x}{n_d}\ \mathrm{for}\ 0\le t\le {n}_d $$

(1)

$$ \frac{d\ {q}_2(t)}{dt}+\theta (t)\ {q}_2(t)=-\overline{D}=-\frac{x}{n_1-{n}_d}\ \mathrm{for}\ {n}_d\le t\le {n}_1 $$

(2)

The solutions of the above differential equations after applying the boundary conditions are given by the following equations:

$$ {q}_1(t)={Q}_m-\overline{D}\ t={Q}_m-\frac{x\ t}{n_d}\ \mathrm{for}\ 0\le t\le {n}_d $$

(3)

$$ {q}_2(t)=\frac{x\ \sigma }{\left({n}_1-{n}_d\right)}\left\{\mathrm{Exp}\left[-\mathrm{Exp}\left[\frac{\left(t-\mu \right)}{\sigma}\right]\right]\left(\mathrm{Ei}\left[{\mathrm{e}}^{\frac{t-\mu }{\sigma }}\right]-\mathrm{Ei}\left[{\mathrm{e}}^{\frac{n_1-\mu }{\sigma }}\right]\right)\right\}\ for\ {n}_d\le t\le {n}_1 $$

(4)

where the integral Ei(x) for (x) ≥ 0 is defined by $\mathrm{Ei}(x)=\underset{-x}{\overset{\infty }{\int }}\frac{e^{-t}}{t}\ dt$ [14]

• If x > Q_m, the following relationships are evident:

$$ \frac{d\ {q}_3(t)}{dt}=-\frac{\overline{D}}{1+\epsilon \left(N-t\right)}=-\frac{x-{Q}_m}{N-{n}_1}\left(\frac{1}{1+\epsilon \left(N-t\right)}\right)\ {n}_1\le t\le N $$

(5)

$$ \frac{d\ {q}_4(t)}{dt}=-\overline{D}\left(1-\frac{1}{1+\epsilon \left(N-t\right)}\right)=-\frac{x-{Q}_m}{N-{n}_1}\ \left(1-\frac{1}{1+\epsilon \left(N-t\right)}\right)\ {n}_1\le t\le N $$

(6)

hence,

$$ {q}_3(t)=-\frac{x-{Q}_m}{\epsilon\ \left(N-{n}_1\right)}\ \left\{\ln \left[1+\epsilon \left(N-{n}_1\right)\right]-\ln \left[1+\epsilon \left(N-t\right)\right]\right\}\ {n}_1\le t\le N $$

(7)

$$ {q}_4(t)=-\frac{x-{Q}_m}{\epsilon\ \left(N-{n}_1\right)}\left\{\epsilon \left(t-{n}_1\right)+\ln \left[1+\epsilon \left(N-t\right)\right]-\ln \left[1+\epsilon \left(N-{n}_1\right)\right]\right\}\ {n}_1\le t\le N $$

(8)

The model for crisp environment

The expected annual total cost for the cycle is composed of expected order cost, expected purchase cost, expected varying deteriorating cost, expected varying salvage cost, expected backorder cost, expected lost sales cost, and expected varying holding cost

• The expected order cost per cycle is given by:

$$ E(OC)={C}_o $$

(9)

• The expected purchase cost per cycle is given by:

$$ E(PC)={C}_p\ \underset{x=0}{\overset{\infty }{\int }}{\int}_0^Nx\ f(x)\ dt\ dx={C}_p\ N\underset{x=0}{\overset{\infty }{\int }}x\ f(x)\ dx $$

(10)

• The expected varying deterioration cost per order is given by:

$$ E(DC)={C}_d\ {N}^{\beta }\ \left(\ {Q}_m-\underset{x=0}{\overset{Q_m}{\int }}{\int}_{n_d}^{n_1}\ D(t)\ f(x)\ dt\ dx\right)\kern0.5em ={C}_d\ {N}^{\beta}\left({Q}_m-\frac{1}{\left({n}_1-{n}_d\right)}\underset{x=0}{\overset{Q_m}{\int }}\left({n}_1-{n}_d\right)\ x\ f(x)\ dx\right)={C}_d\ {N}^{\beta}\left({Q}_m-\underset{x=0}{\overset{Q_m}{\int }}x\ f(x)\ dx\right) $$

(11)

• The expected varying salvage value of deteriorated units per order is given by:

$$ E(VC)={C}_v\ {N}^{\beta}\left({Q}_m-\underset{x=0}{\overset{Q_m}{\int }}x\ f(x)\ dx\right)={C}_d\ \gamma\ {N}^{\beta}\left({Q}_m-\underset{x=0}{\overset{Q_m}{\int }}x\ f(x)\ dx\right) $$

(12)

• The expected backorder cost per cycle is given by:

$$ E(BC)={C}_b\left(\underset{Q_m}{\overset{\infty }{\int }}\underset{n_1}{\overset{N}{\int }}\ \left(-{q}_3(t)\right)\ f(x)\ dtdx\kern0.5em \right)\kern0.5em ={C}_b\ \left[\underset{Q_m}{\overset{\infty }{\int }}\frac{x-{Q}_m}{\epsilon\ }\left(\begin{array}{c}1-\frac{1}{\epsilon\ \left(N-{n}_1\right)}\ln \left[1+\epsilon \left(N-{n}_1\right)\right]\end{array}\right)\ f(x)\ dx\right] $$

(13)

• The expected lost sales cost per cycle is given by:

$$ E(LC)={C}_L\underset{x={Q}_m}{\overset{\infty }{\int }}\underset{n_1}{\overset{N}{\int }}\left(-{q}_4(t)\right)\ f(x)\ dt\ dx\kern0.5em ={C}_L\left\{\underset{Q_m}{\overset{\infty }{\int }}\frac{x-{Q}_m}{\epsilon}\left[\frac{\epsilon\ \left(N-{n}_1\right)}{2}-\left(1-\frac{1}{\epsilon\ \left(N-{n}_1\right)}\ln \left[1+\epsilon \left(N-{n}_1\right)\right]\right)\right]f(x)\ dx\right\} $$

(14)

• The expected varying holding cost at any time per cycle is given by:

$$ E(HC)={C}_h\ {N}^{-\beta}\left[{\int}_0^{Q_m}\left(\underset{0}{\overset{n_d}{\int }}{q}_1(t)\ dt+\underset{n_d}{\overset{n_1}{\int }}{q}_2(t)\ dt\ \right)f(x)\ dx+\underset{Q_m}{\overset{\infty }{\int }}\underset{n_1}{\overset{N}{\int }}\left(-{q}_4(t)\right)\ dt\ f(x)\ dx\right]\kern1em ={C}_h\ {N}^{-\beta}\left\{\underset{0}{\overset{Q_m}{\int }}\left[\left({Q}_m\ {n}_d-\frac{x\ {n}_d}{2}\right)+{\int}_{n_d}^{n_1}\left\{\left(\sum \limits_{i=0}^{\infty}\left(\frac{\mathrm{Exp}\left[-i\ \left(\frac{t-\mu }{\sigma}\right)\right]}{i!}\right)\right)\left[\left(\left(\frac{\mathrm{Exp}\left[\mathrm{Exp}\left[\frac{n_1-\mu }{\sigma}\right]\right]}{\left(\mathrm{Exp}\left[\frac{\mathrm{n}1-\mu }{\sigma}\right]\right)}\right)\sum \limits_{n=0}^{\infty}\left(n!\mathrm{Exp}\left[-n\left(\frac{n_1-\mu }{\sigma}\right)\right]\right)\right)-\left(\left(\frac{\mathrm{Exp}\left[\mathrm{Exp}\left[\frac{t-\mu }{\sigma}\right]\right]}{\Big(\mathrm{Exp}\left[\frac{t-\mu }{\sigma}\right]}\right)\sum \limits_{j=0}^{\infty}\left(j!\mathrm{Exp}\left[-j\ \left(\frac{t-\mu }{\sigma}\right)\right]\right)\right)\right]\right\} dt\right]f(x)\ dx+\underset{Q_m}{\overset{\infty }{\int }}\frac{x-{Q}_m}{\epsilon}\left[\frac{\epsilon\ \left(N-{n}_1\right)}{2}-\left(\begin{array}{c}1-\frac{1}{\epsilon\ \left(N-{n}_1\right)}\ln \left[1+\epsilon \left(N-{n}_1\right)\right]\end{array}\right)\right]f(x)\ dx\right\} $$

(15)

From Eqs. (9), (10), (11), (12), (13), (14), and (15), the expected annual total cost for the cycle is composed of E(TC) = E(OC) + E(PC) + E(DC (N)) + E(VC(N)) + E(BC) + E(LC) + E(HC(N))

$$ {\displaystyle \begin{array}{c}E\left( TC\left({Q}_m,{n}_d,{n}_1,N\right)\right)={C}_o+{C}_p\ N\underset{x=0}{\overset{\infty }{\int }}x\ f(x)\ dx\\ {}+\underset{Q_m}{\overset{\infty }{\int }}\frac{\left(x-{Q}_m\right)}{\epsilon }\ \left[\ \left({C}_b-{C}_h\ {N}^{-\beta }-{C}_L\right)\left(1-\frac{\ln \left[1+\epsilon \left(N-{n}_1\right)\right]}{\epsilon \left(N-{n}_1\right)}\right)+\left({C}_h\ {N}^{-\beta }+{C}_L\right)\frac{\left(N-{n}_1\right)}{\ \epsilon}\right]f(x)\ dx\\ {}+{C}_h\ {N}^{-\beta}\left\{\underset{0}{\overset{Q_m}{\int }}\left[\left({Q}_m\ {n}_d-\frac{x\ {n}_d}{2}\right)+\underset{n_d}{\overset{n_1}{\int }}\left(\left(\sum \limits_{i=0}^{\infty}\left(\frac{\mathrm{Exp}\left[-i\ \left(\frac{t-\mu }{\sigma}\right)\right]}{i!}\right)\right)\left(\left(\frac{\mathrm{Exp}\left[\mathrm{Exp}\left[\frac{n_1-\mu }{\sigma}\right]\right]}{\left(\mathrm{Exp}\left[\frac{\mathrm{n}1-\mu }{\sigma}\right]\right)}\right)\times \sum \limits_{n=0}^{\infty}\left(n!\mathrm{Exp}\left[-n\left(\frac{n_1-\mu }{\sigma}\right)\right]\right)\right)\right.\right)\right.\\ {}\left.\left.\left.-\left(\left(\frac{\mathrm{Exp}\left[\mathrm{Exp}\left[\frac{t-\mu }{\sigma}\right]\right]}{\Big(\mathrm{Exp}\left[\frac{t-\mu }{\sigma}\right]}\right)\sum \limits_{j=0}^{\infty}\left(j!\mathrm{Exp}\left[-j\ \left(\frac{t-\mu }{\sigma}\right)\right]\right)\right)\right)\mathrm{d}t\right]f(x)\ dx\right\}\\ {}+{C}_d\ \left(1+\gamma \right)\ {N}^{\beta}\left({Q}_m-\underset{x=0}{\overset{Q_m}{\int }}x\ f(x)\ dx\right)\end{array}} $$

(16)

This paper puts a constraint on varying deteriorating cost for if the deteriorating cost exceeds a certain limit, this tend to increase the expected annual total cost or lead to loss. The Karush–Kuhn–Tucker (KKT) conditions [15] are first-order necessary conditions for a solution in non-linear programming to be optimal, provided that some regularity conditions are satisfied. Allowing inequality constraints, the KKT approach to nonlinear programming generalizes the method of Lagrange multipliers, which allows only equality constraints. So, this method is suitable to solve this problem.

Consider a limitation on the expected varying deteriorating cost, i.e.:

$$ E(DC)={C}_d\ {N}^{\beta}\left({Q}_m-\underset{x=0}{\overset{Q_m}{\int }}x\ f(x)\ dx\right)\le {k}_d $$

(17)

It may be written as Min E (TC(Q_m, n_d, n₁, N.))

subject to inequality constraint E(DC(Q_m, n_d, n₁, N)) ≤ k_d.

To find the optimal values ${Q}_m^{\ast },{n}_d^{\ast },{n}_1^{\ast }$, and N^∗ which minimize E(TC) under the constraint (17), the Lagrange multipliers technique with the Kuhn-Tacker conditions [15] is used as follows:

$$ {\displaystyle \begin{array}{c}E\left(L\left({Q}_m,{n}_d,{n}_1,N\right)\right)={C}_o+{C}_p\ N\underset{x=0}{\overset{\infty }{\int }}x\ f(x)\ dx\\ {}+\underset{Q_m}{\overset{\infty }{\int }}\frac{\left(x-{Q}_m\right)}{\epsilon }\ \left[\left({C}_b-{C}_h\ {N}^{-\beta }-{C}_L\right)\left(1-\frac{\ln \left[1+\epsilon \left(N-{n}_1\right)\right]}{\epsilon \left(N-{n}_1\right)}\right)\right.\\ {}\left.+\left({C}_h\ {N}^{-\beta }+{C}_L\right)\frac{\epsilon\ \left(N-{n}_1\right)}{2}\right]f(x)\ dx\\ {}+{C}_h\ {N}^{-\beta}\left\{\underset{0}{\overset{Q_m}{\int }}\left[\left({Q}_m\ {n}_d-\frac{x\ {n}_d}{2}\right)\right.\right.\\ {}+\underset{\mathrm{n}\mathrm{d}}{\overset{\mathrm{n}1}{\int }}\left\{\left(\sum \limits_{i=0}^{\infty}\left(\frac{\mathrm{Exp}\left[-i\left(\frac{t-\mu }{\sigma}\right)\right]}{i!}\right)\right)\left[\left(\left(\frac{\mathrm{Exp}\left[\mathrm{Exp}\left[\frac{n_1-\mu }{\sigma}\right]\right]}{\left(\mathrm{Exp}\left[\frac{n_1-\mu }{\sigma}\right]\right)}\right)\right.\right.\right.\\ {}\left.\times \sum \limits_{n=0}^{\infty}\left(\begin{array}{c}n!\\ {} Exp\left[-{n}^{\ast}\left(\frac{n_1-\mu }{\sigma}\right)\right]\end{array}\right)\right)\\ {}\left.\left.\left.\left.-\left(\left(\frac{\mathrm{Exp}\left[\mathrm{Exp}\left[\frac{t-\mu }{\sigma}\right]\right]}{\Big(\mathrm{Exp}\left[\frac{t-\mu }{\sigma}\right]}\right)\sum \limits_{j=0}^{\infty}\left(j!\mathrm{Exp}\left[-j\ \left(\frac{t-\mu }{\sigma}\right)\right]\right)\right)\right]\right\}\mathrm{d}t\right]f(x)\ dx\right\}\\ {}+{C}_d\ \left(1+\gamma \right)\ {N}^{\beta}\left({Q}_m-\underset{x=0}{\overset{Q_m}{\int }}x\ f(x)\ dx\right)+{\lambda}_d\left[\ {C}_d\ {N}^{\beta}\left({Q}_m-\underset{x=0}{\overset{Q_m}{\int }}x\ f(x)\ dx\right)-{K}_d\right]\end{array}} $$

(18)

The optimal values ${Q}_m^{\ast },{n}_d^{\ast },{n}_1^{\ast }$, and N^∗ can be calculated by setting the corresponding first partial derivatives of Eq. (18) equal to zero.

$$ \mathrm{Thus},\mathrm{let}\ g1\left({Q}_m,{n}_d,{n}_1,N\right)=\frac{\partial E\left(L\left({Q}_m,{n}_d,{n}_1,N\right)\right)}{\partial {Q}_m}\left|\begin{array}{c}\\ {}\\ {}{Q}_m={Q}_m^{\ast}\end{array}=0\right., $$

$$ g2\left({Q}_m,{n}_d,{n}_1,N\right)=\frac{\partial E\left(L\left({Q}_m,{n}_d,{n}_1,N\right)\right)}{\partial {n}_d}\left|\begin{array}{c}\\ {}\\ {}{n}_d={n}_d^{\ast}\end{array}=\right.0, $$

$$ g3\left({Q}_m,{n}_d,{n}_1,N\right)=\frac{\partial E\left(L\left({Q}_m,{n}_d,{n}_1,N\right)\right)}{\partial {n}_1}\left|\begin{array}{c}\\ {}\\ {}{n}_1={n}_1^{\ast}\end{array}=\right.0, $$

$$ g4\left({Q}_m,{n}_d,{n}_1,N\right)=\frac{\partial E\left(L\left({Q}_m,{n}_d,{n}_1,N\right)\right)}{\partial N}\left|\begin{array}{c}\\ {}\\ {}N={N}^{\ast}\end{array}=\right.0 $$

$$ and\ g5\left({Q}_m,{n}_d,{n}_1,N\right)=\frac{\partial E\left(L\left({Q}_m,{n}_d,{n}_1,N\right)\right)}{\partial {\lambda}_d}\left|\begin{array}{c}\\ {}\\ {}{\lambda}_d={\lambda}_d^{\ast}\end{array}=\right.0 $$

The goal is to solve the previous multivariable nonlinear system by using Newton’s method using Mathematica program. The following Algorithm is applied.

Step 1: Define G(y) and J(y): Let F be a function which maps ℝⁿ to ℝⁿ and The Jacobian matrix is a matrix of first-order partial derivatives without the equation of the constraint g5 to find the value of K_d as:

$$ G(y)=\left[\begin{array}{c}g1\left({Q}_m,{n}_d,{n}_1,N\right)\\ {}g2\left({Q}_m,{n}_d,{n}_1,N\right)\\ {}g3\left({Q}_m,{n}_d,{n}_1,N\right)\\ {}g4\left({Q}_m,{n}_d,{n}_1,N\right)\end{array}\right],J(y)=\left[\begin{array}{c}\begin{array}{cc}\frac{\partial g1}{\partial {Q}_m}& \frac{\partial g1}{\partial {n}_d}\\ {}\frac{\partial g2}{\partial {Q}_m}& \frac{\partial g2}{\partial {n}_d}\end{array}\ \begin{array}{cc}\frac{\partial g1}{\partial {n}_1}& \frac{\partial g1}{\partial N}\\ {}\frac{\partial g2}{\partial {n}_1}& \frac{\partial g2}{\partial N}\end{array}\\ {}\begin{array}{cc}\frac{\partial g3}{\partial {Q}_m}& \frac{\partial g3}{\partial {n}_d}\\ {}\frac{\partial g4}{\partial {Q}_m}& \frac{\partial g4}{\partial {n}_d}\end{array}\ \begin{array}{cc}\frac{\partial g3}{\partial {n}_1}& \frac{\partial g3}{\partial N}\\ {}\frac{\partial g4}{\partial {n}_1}& \frac{\partial g4}{\partial N}\end{array}\end{array}\right] $$

Step 2: Let y ∈ ℝⁿ. Then y represents the vector $\left[\begin{array}{c}\begin{array}{c}{Q}_m\\ {}{n}_1\\ {}{n}_d\\ {}N\end{array}\\ {}{\lambda}_d\end{array}\right]$

Step3: Assume any initial value y₀ for Q_m, n_d, n₁, and N when λ_d = 0.

Step4: Calculate G(y₀ ), J(y₀) and then find the inverse matrix J⁻¹(y₀), for y₀.

Step 5: Solve the system y₁ = y₀ − J⁻¹(y₀) G(y₀).

Step 6: Use the results of y₁ to find the next iteration y₂ by using the same procedure.

Step 7: Keep repeating the process until finding the same results for two consecutive values of Q_m, n₁, n_d, and N. Then from Eq. (17), it is possible to calculate K_d.

Step 8: Repeat steps 1, 2, 3, and 4 with changing λ_d and adding g5(Q_m, n_d, n₁, N) to the system until obtaining the same results for two consecutive values of Q_m, n_d, n₁, and N. Then these values are the optimal values of ${Q}_m^{\ast },{n}_d^{\ast },{n}_1^{\ast },\mathrm{and}\ {N}^{\ast }.$

Step 9: Thus, the optimal value of the annual expected total cost TC(Q_m, n_d, n₁, N) can be easily calculated.

The model for fuzzy environment

The inventory cost coefficients, elasticity parameters, and other coefficients in the model are fuzzy in nature. Therefore, the decision variables and the objective function should be fuzzy as well. To solve this inventory model using Lagrange multiplier technique, it should be find the right and the left shape functions of the objective function and decision variables, by finding the upper bound and the lower bound of the objective function, i.e., ${\overset{\sim }{L}}^L\left(\propto \right)$ and ${\overset{\sim }{L}}^R\left(\propto \right)$. Recall that ${\overset{\sim }{L}}^L\left(\propto \right)$ and ${\overset{\sim }{L}}^R\left(\propto \right)$ represent the largest and the smallest values (the left and right ∝cuts) of the optimal objective function $\overset{\sim }{L}\left(\propto \right).$ For example using approximated value of TFN of ${\overset{\sim }{C}}_o$ which observe in Fig. 2.

Fig. 2

Order cost as triangular fuzzy number

Consider the model when all parameters are triangular fuzzy numbers (TFN) as given:

$$ {C}_p=\left({C}_p-{\omega}_1,{C}_p,{C}_p+{\omega}_2\right),\kern4.25em {C}_o=\left({C}_o-{\omega}_3,{C}_o,{C}_o+{\omega}_4\right), $$

$$ {C}_h=\left({C}_h-{\omega}_5,{C}_h,{C}_{hr}+{\omega}_6\right),\kern3.75em {C}_b=\left({C}_b-{\omega}_7,{C}_b,{C}_b+{\omega}_8\right), $$

$$ {C}_L=\left({C}_L-{\omega}_9,{C}_L,{C}_L+{\omega}_{10}\right)\kern1.75em and\kern1.75em {C}_d=\left({C}_d-{\omega}_{11},{C}_d,{C}_d+{\omega}_{12}\right). $$

where ω_i, i = 1, 2, …  … , 12 are arbitrary positive numbers under the following restrictions:

$$ 0\le {\omega}_1\le {C}_p,{\omega}_2\ge 0,\kern1.25em 0\le {\omega}_3\le {C}_o,{\omega}_4\ge 0,\kern1.25em 0\le {\omega}_5\le {C}_h,{\omega}_6\ge 0, $$

$$ 0\le {\omega}_7\le {C}_b,{\omega}_8\ge 0,\kern1em 0\le {\omega}_9\le {C}_L,{\omega}_{10}\ge 0\kern1.25em \mathrm{and}\kern1.25em 0\le {\omega}_{11}\le {C}_d,{\omega}_{12}\ge 0. $$

hence, the left and right limits of ∝cuts of C_p, C_o, C_h, C_b, C_L, and C_d are given by:

$$ {{\overset{\sim }{C}}_p}_L\left(\propto \right)={C}_p-\left(1-\propto \right){\omega}_1,\kern2.5em {{\overset{\sim }{C}}_p}_R\left(\propto \right)={C}_p+\left(1-\propto \right){\omega}_2, $$

$$ {{\overset{\sim }{C}}_o}_L\left(\propto \right)={C}_o-\left(1-\propto \right){\omega}_3,\kern2.5em {{\overset{\sim }{C}}_o}_R\left(\propto \right)={C}_o+\left(1-\propto \right){\omega}_4, $$

$$ {{\overset{\sim }{C}}_h}_L\left(\propto \right)={C}_h-\left(1-\propto \right){\omega}_5,\kern2.5em {{\overset{\sim }{C}}_h}_R\left(\propto \right)={C}_h+\left(1-\propto \right){\omega}_6, $$

$$ {{\overset{\sim }{C}}_b}_L\left(\propto \right)={C}_b-\left(1-\propto \right){\omega}_7,\kern2.25em {{\overset{\sim }{C}}_b}_R\left(\propto \right)={C}_b+\left(1-\propto \right){\omega}_8, $$

$$ {{\overset{\sim }{C}}_L}_L\left(\propto \right)={C}_L-\left(1-\propto \right){\omega}_9,\kern2.25em {{\overset{\sim }{C}}_L}_R\left(\propto \right)={C}_L+\left(1-\propto \right){\omega}_{10}, $$

and

$$ {{\overset{\sim }{C}}_d}_L\left(\propto \right)={C}_d-\left(1-\propto \right){\omega}_{11},\kern1.6em {{\overset{\sim }{C}}_d}_R\left(\propto \right)={C}_d+\left(1-\propto \right){\omega}_{12} $$

where

$$ {\overset{\sim }{C}}_p={C}_p+\frac{1}{4}\left({\omega}_2-{\omega}_1\right),\kern2.75em {\overset{\sim }{C}}_o={C}_o+\frac{1}{4}\left({\omega}_4-{\omega}_3\right), $$

$$ {\overset{\sim }{C}}_h={C}_h+\frac{1}{4}\left({\omega}_6-{\omega}_5\right),\kern2.7em {\overset{\sim }{C}}_b={C}_b+\frac{1}{4}\left({\omega}_8-{\omega}_7\right), $$

$$ {\overset{\sim }{C}}_L={C}_L+\frac{1}{4}\left({\omega}_{10}-{\omega}_9\right)\kern0.75em \mathrm{and}\kern1.25em {\overset{\sim }{C}}_d={C}_d+\frac{1}{4}\left({\omega}_{12}-{\omega}_{11}\right). $$

Likewise, the same steps which are taken in the crisp case can be applied here, except that the crisp costs of C_p, C_o, C_h, C_b, C_L, and C_d will be replaced by the fuzzy costs of ${\overset{\sim }{C}}_p,{\overset{\sim }{C}}_o,{\overset{\sim }{C}}_h,{\overset{\sim }{C}}_b,{\overset{\sim }{C}}_L, and\ {\overset{\sim }{C}}_d$. Then the optimal values ${Q}_m^{\ast }$, ${n}_1^{\ast },{n}_d^{\ast }$, and N^∗ which minimize expected annual total cost for fuzzy case can be calculated by using the same previous Algorithm.

Application

Petro-chemical store sells Alcohol that follows a periodic review “order up to Q_m ” with zero lead time. The parameters with 60 samples indicate that demand (see the Appendix) is estimated when α = 0.05 in Table 1. The optimal solutions of the crisp and fuzzy TFN environments using Mathematica program are given in Table 2 and Fig. 3. When f(t) follows Gumbel distribution μ = 0.65, σ = 1.8, ϵ = 0.5, γ= 0.4,η = 2, δ = 0.8351.

Table 1 Crisp and fuzzy values of the parameters

Table 2 Crisp and fuzzy values for Gumbel deterioration

Fig. 3

Crisp and fuzzy value for Gumbel distribution

Conclusion

For the importance of deteriorating in units, this paper investigates probabilistic periodic review inventory model for deteriorating items with varying costs under a varying deteriorating cost constraint, when the demand is a random variable follows Pareto distribution for crisp and fuzzy environments without lead time. Here, this paper calculated optimal values of the four decision variables (maximum inventory level, stock-out time, deteriorating time, and review time) which minimize the expected annual total cost. A numerical analysis method (Newton’s method) was used to solve the system consisting of some nonlinear equations for different values of β. Then the model is illustrated with an application for the purpose of evaluation and validation of the results. It can be concluded that fuzzy environment is closer to the practical situation than crisp case. In addition, when β equals 0.4, it obtains the best value for minimum expected annual total cost.

Notations and assumption

Q _m :

Maximum inventory level (decision variable)

N :

The time of review “cycle” (decision variable)

x :

The demand during the cycle N (random variable)

$\overline{D}$ :

The expected demand per unit item $\overline{D}\equiv \left({\overline{D}}_1,{\overline{D}}_2,\dots, {\overline{D}}_n\right)$

C _o :

The order cost per unit item per cycle

C _p :

The purchase cost per unit item per cycle

C _b :

The backorder cost per unit item per cycle

C _L :

The lost sales cost per unit item per cycle

C _h :

The holding cost per unit item per cycle

C_h(N):

The varying holding cost per unit item per cycle =C_h N^−β

C_d(N):

The varying deterioration cost per order =C_d N^β

C_v(N):

The varying salvage cost per order =C_d γ N^β

γ :

The salvage value associated with deteriorated item

θ(t):

The deterioration rate at time t

k _d :

The goal associated to expected deteriorating cost

E(TC):

The expected total average cost function E( TC(Q_m, n_d, n₁, N))

${\overset{\sim }{C}}_o$ :

The fuzzy order cost per unit item per cycle

${\overset{\sim }{C}}_p$ :

The fuzzy purchase cost per unit item per cycle

${\overset{\sim }{C}}_b$ :

The fuzzy back order cost per unit item per cycle

${\overset{\sim }{C}}_L$ :

The fuzzy lost sales cost per unit item per cycle

${\overset{\sim }{C}}_h$ :

The fuzzy holding cost per unit item per cycle

${\overset{\sim }{C}}_h\ (N)$ :

The fuzzy varying holding cost per cycle $={\overset{\sim }{C}}_h\ {N}^{-\beta }$

${\overset{\sim }{C}}_d(N)$ :

The fuzzy varying deterioration cost per order $={\overset{\sim }{C}}_d\ {N}^{\beta }$

${\overset{\sim }{C}}_v(N)$ :

The fuzzy varying salvage cost per order $={\overset{\sim }{C}}_d\ \gamma\ {N}^{\beta }$

${\overset{\sim }{k}}_d$ :

The fuzzy goal associated to expected deteriorating cost

n ₁ :

The time of stock-out (decision variable)

n _d :

The time of deteriorating (decision variable)

q₁(t):

The inventory level at time t (0 ≤ t ≤ n_d) in which the product has demand

q₂(t):

The inventory level at time t (n_d ≤ t ≤ n₁) in which the product has demand and deterioration

q₃(t):

The inventory level at time t (n₁ ≤ t ≤ N) in which the product has backorder

q₄(t):

The inventory level at time t (n₁ ≤ t ≤ N) in which the product has lost sales

Appendix

The value of the demand (calculated by m³) for Pareto distribution

0.18	0.03	0.12	2.2	0.4	1.53	0.67	0.93	0.21	0.9	0.6	0.14
0.24	0.2	0.7	0.81	1.14	1.22	0.01	0.83	0.3	0.84	0.85	0.16
0.13	0.4	0.5	0.08	0.77	0.11	0.2	2.12	0.15	0.14	0.01	0.25
1.1	0.14	0.51	0.15	0.24	1.72	0.37	0.57	3.54	0.12	0.7	0.09
3.25	1.48	0.05	0.71	0.13	0.29	0.01	0.06	1.11	0.34	0.18	0.6

Goodness of Fit: Kolmogorov–Smirnov

Sample size	60
α	0.05
Critical value	0.17231
P value	0.73526