1 Introduction

1.1 Experimental studies

The flow over inclined flat plates has been the subject of many studies over the past century. This is partly due to the fundamental nature of the problem. In many ways it is considered to be the simplest possible bluff body, because it is associated with fixed separation points and minimized distance between the windward side of the body and the wake region. Moreover, from a practical standpoint, this problem is a simplified representation of many modern day wind engineering applications such as solar panels exposed to extreme winds. This has resulted in renewed interest in investigating this flow problem using state-of-the-art experimental and computational tools.

Previous studies investigate the effects of different geometric parameters such as the aspect ratio (span to chord ratio), inclination angle, planform shape and blockage effects, as well as free stream velocity, on aerodynamic characteristics of inclined flat plates. Table 1 represents a summary of the previous experimental studies on flow over flat plate.

Table 1 A summary of previous experimental studies on flow over inclined flat plate
Full size table

1.1.1 Effect of inclination angle and aspect ratio

Among the experimental studies carried out on flow around inclined flat plate, the experiments by Fage and Johansen [1] have gained significant recognition as a benchmark, due to the comprehensive range of parameters investigated therein. Their experiments dealt with an infinite span plate at different inclination angles in which the behaviors of lift, drag, pressure coefficients, and shedding frequency were investigated. The infinite span term used here refers to a very large span to chord ratio configuration where the two ends of the plate are attached to the tunnel side walls. They performed the experiments at 18 inclination angles ranging from 0.15° to 90° at a speed of 15 m/s. The corresponding Reynolds number based on the chord length of the flat plate at 90° inclination angle was 150,000. Their results quantify the variation of pressure on the windward and leeward sides of the flat plate with increasing angle of incidence, and indicate that the maximum pressure difference between the windward and leeward surfaces occurs when the plate is positioned normal to the flow (i.e., at a 90° incidence angle).

In another set of experiments, they measured the effect of different inclination angles (ranging between 12° to 90°) on the shedding frequency. They noticed an increasing trend for the shedding frequency when the inclination angle increased from 12° to 14°. For the rest of the angles from 14 to 90 degrees, a decreasing trend was observed for the shedding frequency.

To evaluate the influence of the free stream velocity on the shedding frequency, they performed measurements on a normal flat plate (90 degrees) at free stream velocities ranging from 3.2 to 18 m/sec. The results showed that increasing the free stream velocity significantly increases the shedding frequency. At the speed of 3.2 m/sec the shedding frequency was 3.13 Hz, however, by increasing the velocity to 18 m/s, the shedding frequency increased to 17.35 Hz. The Strouhal number based on the shedding frequency, incoming velocity and chord length remained constant at about 0.14.

Effect of different aspect ratios on the flow around inclined flat plate has been investigated by many researchers as listed in Table 1. One of the most comprehensive studies of this effect is the study by Fail et al. [6], who performed wind tunnel tests at a speed of 43 m/sec at aspect ratios ranging from 1 to 20. Based on their definition, the main feature of the flow around a normal flat plate is a closed bubble behind the plate (An example of the generated bubble behind the plate can be observed in Fig. 1). The bubble is defined as the closed part of the mean flow streamlines behind the plate [6].

Fig. 1
figure 1

Schematic of a bubble generated behind a normal flat plate (obtained from current simulation at Re = 150,000)

Full size image

Their results indicate that as the aspect ratio increases, the drag increases, the base pressure and the bubble length behind the plate decrease. They concluded that these changes are small up to an aspect ratio of 10 and thereafter a more rapid change was observed. They also studied the effect of the planform geometry of the inclined flat plate by investigating square, circular and equilateral-triangular planforms of the same aspect ratio, on vortex shedding frequency and drag, and showed that vortex shedding frequency and drag coefficient are functions of the wake width (as defined by the separation between the two shear layers) rather than the planform geometry of the wake generator.

1.2 Numerical simulations

With invention and increasing acceptance of numerical simulation as a capable tool for analysis of complex flows, researchers have used this tool to investigate various aspects of flow around flat plate. The growing capability of computers has strengthened the use of numerical methods. Using the new numerical algorithms by means of supercomputers, scientists are able to simulate highly complex flows and capture the evolution of different flow parameters. Examples of these include Large Eddy and Direct Numerical Simulations (LES, DNS) which present time resolved information of the flow field. Additionally, numerical based post-processing methods such as λ2 or Q criteria which are used in the current study can extract three-dimensional flow structures which seem to be difficult or expensive by using experimental apparatus.

Table 2 summarizes some of the previous numerical studies, which deal with different aspects of numerical simulation of flow around flat plate. In the most broad sense, these studies can be divided into two large categories. Those that focus on the numerical simulation such as new solution methods, and those in which the focus is analysis of the flow, with numerical simulations regarded as a principal or complimentary tool for this analysis.

Table 2 A summary of previous numerical studies on flow over flat plate
Full size table

Here, we briefly review a few selected numerical studies, which demonstrate the increasing level of detail and complexity of the flow analysis achievable thanks to evolution of the numerical techniques over the past two decades. Lasher [25] performed two-dimensional CFD simulation of flow around a flat plate using different turbulence models [25]. Their results showed that the mean value analysis under-predicts the drag force irrespective of the turbulence model. However, the unsteady cases successfully evaluated correct values for this parameter. The Reynolds number was 32,200 based on the chord length and inlet velocity. They tested different turbulence models including standard k − ε, the extended k − ε developed by Chen and Kim [32], RNG k − ε [33] and Speziale [34] turbulence models. Based on their evaluation, the Speziale [34] model which was anisotropic model predicted more close drag coefficients to the experimental values of Takeuchi and Okamoto [35].

Najjar and Vanka [21] used two-dimensional numerical simulation to model flow over a normal flat plate at 80 < Re < 1000. The numerical method was based on a fifth-order upwind scheme for the convective terms and a fourth-order scheme for diffusion term. They used a direct solver according to eigenvalue decomposition and a capacitance matrix technique for the pressure Poisson equation. They observed that the mean drag force is over-predicted by a factor of 1.6 comparing to the value reported by Fage and Johansen [1]. The difference was expected to be due to the initiation of flow three-dimensionality for Reynolds numbers larger than 200. Najjar and Vanka [22] continued their study and performed a three-dimensional Direct Numerical Simulation on flow over a normal flat plate at the Reynolds number of 1000. The mean drag obtained from the simulation showed good agreement with the experimental results. The three-dimensional case was also able to capture the regions of streamwise vorticity in the form of ribs connecting the adjacent vortex rollers. They concluded that the enhancement in the quality of the results from two to three-dimensional case is due to the introduction of three-dimensional effects in the second case.

Taira and Colonius [27] using the immersed boundary method performed three-dimensional numerical simulations of flow around low-aspect-ratio flat plate at Reynolds numbers of 300 and 500 with emphasis on the unsteady vortex dynamics at post-stall angles of attack. They performed an oil tow-tank experiment in order to validate their numerical simulation. They studied the effect of different parameters including the aspect ratio, angle of attack and planform geometry on the flow structure behind the plate. They noticed that the tip vortices significantly influence the vortex dynamics and stabilize the flow which has significant influence on aerodynamic forces. Based on the aspect ratio, angle of attack and Reynolds number, different stability regimes were observed including a) a stable steady state, b) a periodic unsteady state or c) an aperiodic unsteady state. This evaluation was performed by looking at the variation of angle of attack relative to aspect ratio parameter. They noticed that the steady state condition is achieved over a wide range of angles of attack with lower aspect ratios since the tip vortices are able to prevent the leading and trailing edge vortices from shedding. By increasing the aspect ratio, vortex shedding from leading and trailing edges started and a periodic behavior was observed. Although they evaluated flat plates in different flow configurations, their research was carried out at low Reynolds numbers and flow analysis for higher Reynolds numbers was missing.

Tian et al. [30] performed LES to model flow over a normal flat plate with the thickness to height ratio of 0.02 at the Reynolds number of 150,000. The influence of the shape of the corners was investigated in their study. Two round corners with different curvature radii (r = 0.01H and 0.005H) were modeled. The sharper corner (r = 0.005H) case increased the mean drag, fluctuations of drag and lift forces as well as the kinetic energy in the near wake.

Due to the significant resemblance of the flow over flat plate with flow over structures such as solar panels, analysis of flow past flat plate at different inclination angles has gained significant attention by researchers in solar panel field. The main objective of these studies is the analysis of flow over solar panels in atmospheric boundary layer and its influence on the wind loading. Basically researchers in the field of solar panel use the flat plate experiments as a benchmarking criterion for their studies. Shademan and Hangan [36, 37] performed RANS studies on a stand-alone solar panel immersed in atmospheric boundary layer at different inclination angles and azimuthal wind directions to distinguish the critical wind loading conditions. No significant change was observed for the inclination angles analyzed. However, they noticed that for the conditions at which the wind is perpendicular either to the front or back face, the panel experiences the maximum wind loading. Although their analysis presented important information for solar panel industry, it did not include any peak value results which require unsteady simulation. Further to this study, Shademan et al. [38] carried out another RANS study on the effect of gap spacing between individual panels and different ground clearance on the wind loading of the solar panels. For the gap spacing they modeled, no significant change was noticed for the experienced wind loading. They also observed that increasing the ground clearance has a large influence on the increase of the wind loading. They concluded this as a result of higher shear flow interaction separated from the bottom and top edges of the panel in higher ground clearance cases. Due to the important effect of ground clearance on the generation of unsteady wind fluctuations, Shademan et al. [39] performed Detached Eddy Simulation (DES) on solar panels with different ground clearance. They noticed that by increasing the ground clearance, the mean and peak wind loading increases. They also found an optimum ground clearance for solar panels at which they experience the least wind loading.

According to the literature, there are various types of experiments (Table 1) and numerical simulations (Table 2) on flow over flat plate. In the experimental side, most of these studies are reporting the mean value results and in numerical side are dealing with modeling issues. It is observed that a comprehensive document which evaluates different aspects of flow over flow plate including the aspect ratio and inclination angle and their effects on different flow parameters such as shedding frequency and aerodynamic loading is missing.

Therefore, in the current study, it is of interest to investigate the effect of different aspect ratios and inclination angles on the mean and unsteady flow parameters. The results of this research can help to a better understanding of the trend of the unsteady aerodynamic loading of flat plate in different configurations. Due to the resemblance of the flow field with flow over solar panels [36,37,38,39], the results of current study can be used as guidance for the design of these kinds of structures.

To achieve the discussed objectives, the manuscript is formed as following: Section 2 provides details of the numerical method including the geometry modeling, governing equations and boundary conditions. In section 3 which is the benchmarking part, the numerical setup used in the current analysis is evaluated by comparing the results with the available experimental data. Finally, section 4 presents the analysis of the results and discussions.

2 Numerical method

2.1 Geometry modeling and boundary conditions

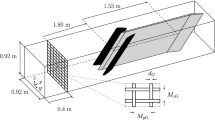
The geometry of flat plate modeled in the current study is similar to the one tested by Fage and Johansen [1] which has a chord length of 0.15 m. The front surface of the plate is flat while the other is slightly tapered from the center (Fig. 2b). The geometry is simulated at three different inclination angles including α = 30°, 60° and 90° for three aspect ratios (S/C) of 0.5, 2 and 5, where S is the span and C is the chord length of the plate. According to the recommendations by Bosch and Rodi [40], the domain dimensions are chosen in a way to have the negligible blockage effect on the plate at above mentioned configurations. The computational domain is taken to extend 20S in the downstream direction and 5S in vertical, transverse and upstream directions from the plate, as illustrated in Fig. 2a. Based on these domain dimensions, the maximum blockage in all cases is about 1%, which is much smaller than the 3% maximum value suggested by Franke et al. [41].

Fig. 2
figure 2

a) Domain dimension and boundary conditions, b) Definition of inclination angle

Full size image

The two sides (left and right), top and bottom boundaries were set to have slip condition. This is identical to a far field free stream surface. The plate surface is considered to be a solid wall with no-slip, no penetration conditions. A uniform air velocity of 15 (m/s) is applied at the inlet of the domain, which is similar to the air velocity considered by Fage and Johansen [1] in their experiments. The corresponding Reynolds number is 150,000 based on the chord length of the plate and incoming air velocity. According to the length of the downstream region (20S), it is expected to have a fully developed flow at the exit of the domain. A ZeroGradient boundary condition which imposes zero changes for the flow parameters is used at the exit boundary. A fully structured mesh scheme was generated for the domain including hexahedral elements in all three directions. In order to capture the high velocity gradients, a finer mesh was considered for the wall proximity region in three directions. The LES mesh study criterion, recommended by Piomelli and Chasnov [42] (∆x+ ≅ 100, y+ ≅ 1 and ∆z+ ≅ 30) is satisfied for regions of interest close to the plate (− 1 < x/C < 1, − 1 < y/C < 1 and − 1 < z/C < 1). In these equations, ∆x+, ∆z+ and y+ are non-dimensional numbers (∆x+ = ∆x uτ/ν, ∆z+ = ∆z uτ/ν, y+ = uτy/ν), where uτ is the friction velocity, y is the normal distance from the wall and ν is the kinematic viscosity. Three inclination angles were modeled for each aspect ratio, which results in a total number of nine simulation cases. Details of the computational domain and mesh generated for each case are shown in Table 3.

Table 3 Details of the computational domain and mesh
Full size table

2.2 Governing equations

The governing equations used in LES are obtained by filtering the unsteady Navier-Stokes equations in Fourier space. The filtered equations are as follows:

$$ \frac{\partial }{\partial {\mathrm{x}}_{\mathrm{i}}}\left({\overline{\mathrm{u}}}_{\mathrm{i}}\right)=0 $$
(1)
$$ \frac{\partial }{\mathrm{\partial t}}\left({\overline{\mathrm{u}}}_{\mathrm{i}}\right)+\frac{\partial }{\partial {\mathrm{x}}_{\mathrm{j}}}\left({\overline{\mathrm{u}}}_{\mathrm{i}}{\overline{\mathrm{u}}}_{\mathrm{j}}\right)=\frac{\partial }{\partial {\mathrm{x}}_{\mathrm{j}}}\left(\upnu \frac{\partial {\upsigma}_{\mathrm{i}\mathrm{j}}}{\partial {\mathrm{x}}_{\mathrm{j}}}\right)-\frac{1}{\uprho}\frac{\partial \overline{\mathrm{p}}}{\partial {\mathrm{x}}_{\mathrm{i}}}-\frac{1}{\uprho}\frac{\partial {\uptau}_{\mathrm{i}\mathrm{j}}}{\partial {\mathrm{x}}_{\mathrm{j}}} $$
(2)

where i indicates the spatial dimension, p is the pressure, ρ is the density, ν is the kinematic viscosity, \( {\overline{\mathrm{u}}}_{\mathrm{i}} \) is the resolved velocity field and τij is the subgrid scale stress defined by:

$$ {\uptau}_{\mathrm{i}\mathrm{j}}=\uprho \overline{{\mathrm{u}}_{\mathrm{i}}{\mathrm{u}}_{\mathrm{j}}}-\uprho \overline{{\mathrm{u}}_{\mathrm{i}}}\overline{{\mathrm{u}}_{\mathrm{j}}} $$
(3)

The subgrid-scale stresses resulting from the filtering operation are unknown, and require modelling. In the current simulations, the dynamic Smagorinsky method [43] is used for modelling the subgrid-scale stresses.

The finite volume method is used to discretize the governing equations. Central differencing scheme was used for discretizing the convective terms. A fully implicit second order method was used for time marching. In order to maintain the courant number less than one, the time step is kept at 1 × 10− 5 (s). For coupling the velocity and pressure, the SIMPLE algorithm was implemented. The OpenFOAM (2.2.3) source code [44] was used for solving the governing equations. The mean value flow parameters are obtained by averaging the unsteady results long after the flow has reached a fully established condition. During the simulations, the drag force exerted on the plate was monitored, and the solution was considered converged when no significant change in the repetitive behavior of the drag force in time was observed. For all results presented in this paper, the continuity and momentum equation residuals are all of the order of 10− 5.

2.3 Validation of the numerical model

In order to evaluate the accuracy of the numerical model, the experiments carried out by Fage and Johansen [1] on flow past flat plate were modeled at different inclination angles. In their experiments, the flat plate was mounted vertically with a small gap between its ends and the floor and roof of the wind tunnel. Different flow parameters including pressure distribution around the plate and Strouhal number were captured at different inclination angles.

Large Eddy Simulations (LES) were performed to model the flow past flat plate at different inclination angles including α = 30°, 50°, 90°. The numerical simulation was designed in a way to mimic the experimental setup carried out by Fage and Johansen [1]. The plate modeled has a span of 1.5 m and a chord length of 0.15 m. The cross section of the flat plate modeled is presented in Fig. 2b. The recommendations by Bosch and Rodi [40] were used to define the domain dimensions in order to reduce blockage issues. Slip condition (zero shear stress) was applied on top, bottom and two side boundaries, and for the plate, a wall boundary condition was used. A uniform velocity of 15 (m/s) corresponding to a Reynolds number of 1.5 × 105 based on the chord length of the plate was applied at the inlet. Note that, the LES mesh requirement criterion [42] was also applied in this section. A fully structured mesh scheme was generated for the domain with a total of 5.9 × 106 cells. Temporal averaging of the unsteady results was performed over a large number of shedding periods (~ 20).

A comparison between the mean pressure coefficient (\( {\mathrm{C}}_{\mathrm{P}}=\left(\mathrm{P}-{\mathrm{P}}_{\infty}\right)/\left(0.5{\uprho}_{\infty }{\mathrm{U}}_{\infty}^2\right) \)) obtained from current simulations and the experiments by Fage and Johansen [1] are presented in Fig. 3a, c, e. Good agreement observed between the two sets of results confirms the validity of the model for the analysis of mean flow over flat plate at different configurations.

Fig. 3
figure 3

Mean pressure coefficients and sectional streamlines at the mid-span a, b) α = 30°, c, d) α = 50° and e, f) α = 90° (x’ is the chordwise distance and x is the global x coordinate)

Full size image

Figures 3b, d, f visualize the mean pressure coefficient contours for α = 30°, 50° and 90°, respectively. These figures show that the size of the recirculation region behind the plate increases as the inclination angle increases. The size of the region was observed to extend to x/C = 1.5 for α = 30°, x/C = 1.7 for α = 50° and x/C = 3 for α = 90°. By increasing the inclination angle to α = 90°, the temporally averaged shape of the recirculation region becomes symmetric and the pressure difference reaches the maximum value relative to α = 30° and 50° cases.

To further evaluate the accuracy of the numerical model in temporal space, the vortex shedding frequency determined from current simulations at different inclination angles were compared with the available experimental results. In this regard, Fast Fourier Transform (FFT) was performed on the time history of aerodynamic forces of the plate. The Strouhal numbers (fc/U∞) calculated based on the peak frequency (f) as captured from the power spectra graphs (Figs. 4a-c), chord length (c) and approaching free stream velocity (U∞) are summarized in Table 4.

Fig. 4
figure 4

Power spectra at a) α = 30°, b) α = 50°, c) α = 90°

Full size image
Table 4 Strouhal number comparison obtained from experiments and current LES
Full size table

Good agreement can be observed between the results obtained from current LES and experiments for 30° and 50° inclination angles. A marginal difference of 7% can be seen between the results of LES and experiments for 90° case. This evaluation confirms the accuracy of the numerical model for the unsteady analysis of flow over flat plate. The analysis discussed herein provides guidelines to expand the numerical simulation to model the flow over flat plates with different aspect ratios at different inclination angles, as described in the following chapters.

3 Mean flow results (effect of aspect ratio and inclination angle)

3.1 Mean aerodynamic forces

In this section, it is of interest to investigate the behaviour of mean aerodynamic forces with different aspect ratios and inclination angles. In this regard, the variation of drag and lift coefficients (CD, CL) for different aspect ratios (0.5, 2 and 5) and inclination angles (30°, 60° and 90°) are presented in Figs. 5a, b and c, d respectively. The aerodynamic force coefficients can be determined using the following equations:

$$ {\mathrm{C}}_{\mathrm{D}}=\frac{{\mathrm{F}}_{\mathrm{D}}}{0.5\uprho {\mathrm{U}}_{\infty}^2\mathrm{A}} $$
(4)
$$ {\mathrm{C}}_{\mathrm{L}}=\frac{{\mathrm{F}}_{\mathrm{L}}}{0.5\uprho {\mathrm{U}}_{\infty}^2\mathrm{A}} $$
(5)

where, FD and FL are drag and lift forces, respectively, ρ is density, A is the area of the plate facing the flow stream (projected frontal area) and U∞ is the free stream velocity.

Fig. 5
figure 5

Variation of CD and CL with a, b) inclination angle and c, d) aspect ratio

Full size image

Figures 5a, b show the variation of drag and lift coefficients with inclinations angle at different aspect ratios. These coefficients were obtained after performing the averaging process over a large number of time steps on the unsteady values. The results show that in general, increasing the inclination angle, increases the drag and reduces the lift irrespective of the aspect ratio. However, higher aspect ratios are associated with larger drag changes when the inclination angle increases from 30° to 90°. An opposite trend is observed for lift coefficient where, bigger changes occur for smaller aspect ratios when moving from 30° to 90° inclinations angles. The comparison of the results for 30° < α < 60° and 60° < α < 90° also shows that the increase of the drag and reduction of the lift are larger for 30° < α < 60°.

The variation of the drag and lift forces with the aspect ratio at different inclination angles are presented in Figs. 5c, d. An increasing trend can be noticed for drag when the aspect ratio increases for 60° and 90° inclination angles. However, lift coefficient does not show significant change for these two inclination angles. An irregular trend was observed for α = 30°, where the drag and lift coefficients show larger values at AR = 0.5 relative to other aspect ratios. From AR =0.5 to AR =2, a reducing trend can be seen for both drag and lift coefficients for this specific inclination angle (α = 30°), however, for AR = 2 to AR = 5, an increasing trend was observed. This phenomenon might be due to the influence of the flow structures in the wake region which causes larger pressure difference between windward and leeward faces of the plate for this specific case. The mean pressure distribution curves presented in the next section present more details regarding this phenomenon.

3.2 Mean pressure distribution

In order to investigate the variation of the mean lift and drag coefficients with the aspect ratio and inclination angle, it is possible to look at the pressure changes in the windward and leeward surfaces of the mid-plane.

Figures 6a-c show mean pressure coefficients for different aspect ratios including AR = 0.5, 2 and 5 at three inclination angles of α = 30°, 60° and 90° extracted at x-y mid-plane of the plate.

Fig. 6
figure 6

Pressure coefficient (CP) for different aspect ratios at a) α = 30°, b) α = 60°, c) α = 90°

Full size image

Figure 6a shows that at α = 30°, increasing the aspect ratio from 2 to 5 results in marginal reduction in the wake pressure which is associated with small increase in the aerodynamic loading on the plate. This is associated with the increase observed in drag coefficient for α = 30° when moving from AR = 2 to AR = 5 as shown in Fig. 5c. At AR = 0.5, a large reduction in the wake pressure is observed particularly in 0 < x/C < 0.3 relative to other aspect ratios. This is associated with higher aerodynamic loading for this specific case.

At α = 60° (Fig. 6b), no significant change in Cp distributions is noticed when aspect ratio increases from 0.5 to 5. This confirms that increasing the aspect ratio from 0.5 to 5 is not expected to cause a significant change in the aerodynamic loading for this inclination angle. This is another interpretation for the trend observed in Figs. 5c, d where almost no change was observed for the drag and lift coefficients when moving from AR = 0.5 to AR = 5 at α = 60°. At α = 90° (Fig. 6c), increasing the aspect ratio from 0.5 to 5 reduces the pressure coefficient at the proximity of the two edges of windward side of the plate. For the leeward side, a reduction in pressure coefficient is observed when aspect ratio increases from 0.5 to 5. The influence of this behavior was seen on mean drag and lift coefficients (Figs. 5c, d) where moving from AR = 0.5 to 5 at α = 90° resulted in slight increase for drag and no change for lift.

Note that, the analysis presented in this study is limited to aspect ratios between 0.5 and 5, however comparison of the results with the infinite span cases (Fig. 3a, c, e) proves existence of much larger pressure differences between front and back surfaces of the infinite span cases compared to smaller aspect ratio cases.

In order to evaluate the pressure coefficients in mid-sections of each case, Fig. 7a-i are presented which show the mean pressure coefficient (Cp) contours and sectional streamlines at different inclination angles and aspect ratios plotted at x-y mid-plane. The irregular behaviour of the pressure coefficient at α = 30° and AR = 0.5 (Fig. 6a) can be explained by examining Fig. 7a. According to Fig. 7a, there is a vortex close to the top corner in the leeward face which results in a lower pressure relative to other regions of the back surface. In this particular case, separation does not dominate the entire back surface and flow reattaches after separation. This was seen in Fig. 6a where the low pressure curve was present only for a very small region of the back surface, and for other parts, it was close to the level of the other aspect ratio cases. By increasing the inclination angle to α = 60° and 90° while keeping the aspect ratio constant, the distance of the vortices from the leeward surface increases in the wake region (Figs. 7b, c). Although a bigger wake region is observed for these two cases compared to α = 30°, they show more positive pressures (− 0.5 < Cp < 0) compared to α = 30° case where − 1 < Cp < − 1.5. For the frontal area (windward surface), the Cp varies between 0 < Cp < 1 for all cases at this specific aspect ratio.

Fig. 7
figure 7

Pressure coefficient contours at a) α = 30°, AR = 0.5, b) α = 60°, AR = 0.5, c) α = 90°, AR = 0.5, d) α = 30°, AR = 2, e) α = 60°, AR = 2, f) α = 90°, AR = 2, g) α = 30°, AR = 5, h) α = 60°, AR = 5, i) α = 90°, AR = 5

Full size image

At AR = 2 and 5 and for similar inclination angles, the flow pattern in the wake region is very close to each other with minor differences in the length of the recirculation regions. Figure 7g shows at AR = 5, the vortices are closer to the plate relative to AR = 2 (Fig. 7d). By moving to α = 60°, the recirculation region expands and becomes elongated towards the downstream (Figs. 7e, h). At α = 90°, the recirculation regions reach their maximum length relative to the previous cases and follow a symmetrical behvaiour (Figs. 7f, i). A maximum recirculation length of x/C = 2.5 was observed for AR = 0.5, x/C = 4 for AR = 2 and x/C = 5 for AR = 5 at α = 90°.

According to Fig. 7a (AR = 0.5, α = 30°), the Cp values in the wake region at the proximity of the top edge are close to − 1.5 which is significantly lower than Cp values in the leeward region of the other cases. Three-dimensional flow structure visualization can help to a better understanding of the phenomena occurring in this case (Fig. 7a). In this regard, the λ2 criterion is used to visualize the flow structures in different flow configurations in the next section.

3.3 Mean flow structures

Different visualization methods can be employed to demonstrate the three-dimensional flow structures behind the plate at different aspect ratios and inclination angles. Jeong and Hussain [45] developed the λ2 criterion which can be used to identify the core of the vortices in the flow field, based on the fact that these cores are related to the locations of minimum pressure in the flow. They derived the λ2 criterion by calculating the gradient of the Navier-Stokes equation and decomposing the acceleration gradient term into symmetric and antisymmetric parts, expressed as SijSij + ΩijΩij, where Sij and Ωij are the symmetric and antisymmetric parts of the velocity gradient tensor, respectively. The Hessian of the pressure can then be connected to the vortical motions in the flow. According to the theory of multivariable calculus, the SijSij + ΩijΩij tensor has three real eigenvalues (λ1 ≥ λ2 ≥ λ3). The point of local pressure minimum requires two eigenvalues of this tensor to be negative. λ2, which corresponds to the second largest eigenvalue of this tensor, is representative of the local pressure minima region. In the current study, the iso-surfaces of λ2 are used for visualizing mean and instantaneous vortices in the flow.

The pressure curves and contours presented in Figs. 6 and 7 are extracted at the mid-plane and do not present any information about the three-dimensional flow pattern across the entire span. Therefore, fig. 8a-i are presented to demonstrate the three-dimensional mean flow structures at different aspect ratios and inclination angles (cases discussed in Figs. 6 and 7) by using λ2 iso-surfaces colored by streamwise vorticity. By visualizing the three-dimensional structures, it is possible to find a more comprehensive explanation for the pressure distribution in the wake region and consequently the resulting aerodynamic forces. Coloring the λ2 iso-surfaces by streamwise vorticity also helps to specify the direction of the vortcies separated from edges and corners of the plate.

Fig. 8
figure 8

Iso-surface of λ2 colored by streamwise vorticity at a) α = 30°, AR = 0.5, b) α = 60°, AR = 0.5, c) α = 90°, AR = 0.5, d) α = 30°, AR = 2, e) α = 60°, AR = 2, f) α = 90°, AR = 2, g) α = 30°, AR = 5, h) α = 60°, AR = 5, i) α = 90°, AR = 5

Full size image

Figures 8a-c show the flow structures at AR = 0.5 and α = 30°, 60°, 90°, respectively. According to Fig. 8a, due to having a short span, the two tip vortices are suppressing the expansion of the bubble behind the plate separated from the leading edge. Therefore, the separation bubble becomes significantly smaller in length and pressure magnitude comparing to other cases. The vorticity contours show opposite senses of rotation for the two tip vortices.

At AR = 0.5 and α = 60°, the influence of tip vortices on flow separation from the top and bottom edges is reduced. A larger separation bubble in length is observed comparing to α = 30° and AR = 0.5 case. This is due to the presence of the two tip vortices (with opposite senses of rotation) which have become smaller and got closer to the bottom corners of the plate. At AR = 0.5 and α = 90°, due to the symmetrical position of the geometry with respect to the flow (comparing to α = 30° and α = 60° cases), four vortices are generated which is different from the previous cases where there was only two vortices. This is because of the identical influence of the four corners in generation of the vortices. Note that, due to the inclination of the plate in α = 30° and α = 60°, only the top two corners were the cause for the generation of the vortices. For this case, flow structures in the wake region show symmetrical pattern in x-y and x-z planes. The tip vortices along the diagonal show similar rotational directions.

At AR = 2, due to longer span comparing to AR = 0.5, the tip vortices have less influence on suppressing the separating flow from the top and bottom edges of the plate. This causes bigger separation bubbles comparing to the ones observed at AR = 0.5. Similar to the flow pattern observed at AR = 0.5, two vortices are generated at α = 30° and α = 60° and four at α = 90°. Symmetrical flow structures with similar rotations are observed along the diagonal of the plate at α = 90° (Fig. 8f).

At AR = 5, four separated tip vortices can be seen for all inclination angles (Figs. 8g-i). They were not present at α = 30° and α = 60° for AR = 0.5 and AR = 2. This can be due to the much longer span for the AR = 5 cases comparing to the other aspect ratios in the current study. At α = 30°, the vortices generated from the top corners are smaller in size and are located between the vortices from the bottom corners (Fig. 8g). As inclination angle increases to 60° and 90°, the two side tip vortices get close to each other and the two middle ones move to the top. It can be seen that at 90°, the tip vortices have a symmetrical pattern both in x-y and x-z planes.

Due to the importance of the unsteady aerodynamic loads, next section describes the variation of the unsteady loads with different aspect ratio and inclination angle configurations mentioned above.

4 Unsteady results

4.1 Effect of inclination angle and aspect ratio on aerodynamic loading

It is also of interest to investigate the behaviour of the unsteady aerodynamic loads (peak values) with respect to different aspect ratios and inclination angles. Unsteady aerodynamic loads on a flat plate play an important role in the design of structures such as solar panels and signs whose flow fields resemble that of flat plate. Due to the shape of the structure which is associated with sharp edges, unsteady aerodynamic fluctuations are inevitable. Such information can help design engineers for a better understanding of flow field and consequently manufacturing more reliable structures against wind loading.

As a measure of the unsteady aerodynamic loads, the standard deviation of the time series of drag and lift forces (CD, STD and CL, STD) are presented in fig. 9a, b for the aspect ratios and inclination angles evaluated in this study. These values are obtained after performing the averaging on aerodynamic loads over a large number of time steps. Figures are arranged as 3D bar charts to demonstrate the effect of changing the inclination angle while the aspect ratio is fixed as well as the effect of aspect ratio while the inclination angle is fixed. By showing the results in the form of bar chart graph, the trade-off and connection between lift and drag forces for different aspect ratios and inclination angles are demonstrated.

Fig. 9
figure 9

Standard deviation of a) drag force and b) lift force at α = 30°, 60°, 90° and AR = 0.5, 2, 5

Full size image

According to Fig. 9a, b, no fluctuation was observed at α = 30° and AR = 0.5 case. This behavior was expected based on the presence of the two tip vortices and their influence on the control of the vortex shedding generated from the top and bottom edges. Unsteady flow visualization can explain the flow phenomenon at this specific case.

By moving to AR = 2 and AR = 5 at α = 30°, a significant increase for both lift and drag fluctuations was seen, however, this increase is much larger for the lift coefficient (0 < CD, STD < 0.02 and 0 < CL, STD < 0.035).

The increasing trend for the standard deviation of the aerodynamic loads continues at α = 60° when moving from AR = 0.5 to AR = 2 and then AR = 5.

At α = 90°, a reducing trend for drag and no change for lift was observed when moving from AR = 0.5 to AR = 5.

Analysis of results at a fixed aspect ratio with different inclination angles reveals that, at AR = 0.5, by increasing the inclination angle, the CD, STD increases. Lift shows similar trend for this range except for 90°, which generates a value close to zero.

At AR = 2, increasing the inclination angle shows that CD, STD remains constant between α = 30° and 60° and increases at 90°. A reducing trend can be seen for CL, STD for this range of inclination angles.

At AR = 5, the CD, STD and CL, STD are showing similar trend when increasing the inclination angle between 30° and 90°. Both parameters are reduced when the inclination angle increases from 30° to 90° at this specific aspect ratio. These above-mentioned trends of variation of the unsteady aerodynamic loads with inclination and aspect ratio will be explained in Section 4.2 based on the unsteady flow structures.

Figures 9a, b also show the configurations at which the plate experiences the maximum peak of the drag and lift forces. Therefore, these configurations can be considered as the critical cases among all the cases analyzed. It can be seen that α = 30° and AR = 5 as well as the α = 90° and AR = 0.5 are the two cases with the highest standard deviation for the drag force. The highest peak for the lift happens at α = 30° and AR = 5.

Finally, different behaviors observed for the aerodynamic fluctuations can be explained by looking at the unsteady flow structures. Next section will evaluate the connection between the standard deviation of aerodynamic loads with the flow structures in the wake region for each aspect ratio and inclination angle.

4.2 Unsteady flow structures

In order to explain the trend of the unsteady forces (CD, STD and CL, STD) observed in Figs 9a, b, unsteady flow structures behind the plate at the mentioned aspect ratios and inclination angles are visualized in Figs. 10a-i using the iso-surfaces of λ2 criterion superimposed onto the streamwise vorticity contours. For each case, a large number of time steps have reached in order to better visualize the shedding of vortices in the wake region.

Fig. 10
figure 10

Iso-surface of λ2 criterion colored by streamwise vorticity at a) α = 30°, AR = 0.5, b) α = 60°, AR = 0.5, c) α = 90°, AR = 0.5, d) α = 30°, AR = 2, e) α = 60°, AR = 2, f) α = 90°, AR = 2, g) α = 30°, AR = 5, h) α = 60°, AR = 5, i) α = 90°, AR = 5

Full size image

Figures 10a-c show the unsteady flow structures at AR =0.5 and α = 30°, 60° and 90°, respectively. Comparison of the mean and unsteady λ2 iso-surfaces at AR =0.5 and α = 30° (Figs. 8a and Figs. 10a) shows a strong similarity between the flow structures observed in these two cases, indicating a stable wake with no large scale periodicity in this case. The two clockwise and counterclockwise tip vortices prevent the propagation of the leading edge recirculation zone in the downstream direction (Fig. 8a), thus stopping the periodic shedding wake vortices for this specific case. At α = 60° (Fig. 10b), the effect of tip vortices is reduced and shedding starts to develop from the top and bottom edges. This separated flow from the top and bottom edges of the plate influences the tip vortices in the wake region. At α = 90° (Fig. 10c), due to the symmetry in geometry, the separated flow from the top and bottom edges influences similarly the tip vortices in the wake region. Therefore, the observed vortices are similar in size and rotation along the diagonal of the plate.

At AR = 2 and α = 30°, 60°, due to the larger distance between the two tip vortices compared to AR = 0.5, the leading and trailing edge vortices have more freedom for interaction and therefore periodic shedding results in a vortex street. The tip vortices are more influenced by the separating flow from the top and bottom edges at α = 60° than α = 30° due to the stronger interaction at this inclination angle. At α = 90°, identical separated flow from the top and bottom edges performs similarly in influencing the vortices in the wake region. The tip vortices are significantly influenced and have almost lost their round shape comparing to other cases (α = 30°, 60°).

At AR = 5 (Figs. 10g-i), the influence of the tip vortices on the leading and trailing edge vortices due to larger span relative to other aspect ratios is further reduced, and the leading and trailing edge vortices shed into the wake without significant decay or cancellation due to the effect of the tip vortices. As a result, the body is exposed to higher fluctuations of the unsteady aerodynamic loads, as evidenced by the standard deviation values in Figs 9a, b. At α = 30°, the separated flow from the top and bottom edges has insignificant influence on the tip vortices. As observed in Fig. 10g, the tip vortices keep their round shape at this specific inclination angle. At α = 60°, since the tip vortices get close to each other, they are influenced by separated flow generated from top and bottom edges. This interaction is more severe at α = 90°, where the tip vortices are significantly influenced by separated flow. As a result, these vortices have lost their round shape at this specific aspect ratio and inclination angle.

In general, the results show a correlation between the intensity of the unsteady aerodynamic loads, and the influence of the tip vortices on the leading edge and trailing edge vortices, which is decreased in the cases with higher aspect ratios, where the spacing between the tip vortices is larger. Basically, the larger the distance between the tip vortices is, the stronger happens the shedding of leading and trailing edges and unsteady loads.

As illustrated in the presented figures, the distance between tip vortices is a key factor for controlling the strength of the shedding vortices and unsteady aerodynamic fluctuations.

5 Conclusion

Large Eddy Simulations have been carried out to investigate flow structures and unsteady aerodynamic loads of a thin flat plate at different geometric and flow configurations represented by different aspect ratios and inclination. For validation purposes, results obtained from the numerical model have been compared with the available experimental data. The good agreement observed between the results confirms the validity of the numerical model.

Analysis of the mean flow results shows a strong dependence of the aerodynamic forces with the aspect ratio and inclination angle. Increase of the inclination angle at each aspect ratio increases drag and reduces the lift force. Increasing the aspect ratio while the inclination angle is constant shows an increase in drag while the lift force remains unchanged.

Among all the aspect ratios and inclination angles investigated, the AR = 0.5 case at α = 30° shows an irregular behavior where the drag and lift are found to be maximum in that specific combination of inclination angle and aspect ratio.

The λ2 iso-surfaces superimposed with streamwise vorticity contours were used to visualize the mean and unsteady flow structures. The iso-surfaces of λ2 criterion show how the inclination angle and aspect ratio parameters influence the vortex shedding phenomenon.

A stable wake with the presence of two tip vortices is observed at AR = 0.5, α = 30° which results in minimal fluctuation of aerodynamic forces at this specific case. At α = 60°, also two tip vortices were present and at α = 90°, due to the symmetry, four vortices appeared. At AR = 2, due to the longer span, the leading and trailing edge vortices have more freedom for shedding and consequently larger unsteady aerodynamic forces are observed for those cases. At AR = 5, the span is even longer than the other aspect ratios and this results in more freedom for flow moving from leading and trailing edge to influence the wake. The four tip vortices which are present in all inclination angles at this aspect ratio interact with the flow from leading and trailing edge, and as a result, large aerodynamic force fluctuations were observed comparing to other aspect ratios.

In general, the results show a correlation between the intensity of the unsteady aerodynamic loads, and the influence of the tip vortices on the leading edge and trailing edge vortices, which is decreased in the cases with higher aspect ratios, where the spacing between the tip vortices is larger. Basically, for cases with a larger gap between the tip vortices, the leading and trailing edge vortices have more freedom for shedding and consequently larger unsteady aerodynamic forces are observed for those cases, while for cases with smaller gap, the shedding from leading and trailing edges are weakened and controlled.