Introduction

Understanding the behaviour of retaining walls subjected to earth pressures is an interesting but a complex phenomenon. As far as the study on passive earth pressures is concerned, several researchers contributed to this problem by conducting experiments on a model retaining wall (Rowe and Peaker, 1965; Narain et al., 1969; Fang et al., 1994, 1997 and 2002; Kobayashi, 1998; Gutberlet et al., 2013). Based on these model test results, the back calculated earth pressure coefficients were then presented in the form of charts and tables by some of the aforementioned researchers.

Though the results obtained from the experiments are one of the reliable options, practically it is not possible to obtain the design coefficients for the various combinations of soil frictional angle ϕ, wall frictional angle δ and sloping backfill angle i. Therefore, it is necessary to rely on the theoretical investigations for the computation of earth pressure coefficients; with the utmost priority of safety of structures under consideration.

Several researchers have studied this problem using different methods such as limit equilibrium (Coulomb, 1776; Rankine, 1857; Terzaghi, 1943; Shields and Tolunay, 1973; Kumar and Subba Rao, 1997; Luan and Nogami, 1997; Soubra et al., 1999; Subba Rao and Choudhury, 2005; Reddy et al., 2013), limit analysis (Chen and Rosenfarb, 1973; Chen, 1975; Soubra, 2000; Soubra and Macuh, 2002; Antão et al., 2011), the method of characteristics (Sokolovski, 1965; Kumar and Chitikela, 2002; Cheng, 2003) and other numerical techniques such as the finite difference method (Benmeddour et al., 2012) and finite element method (Elsaid, 2000; Antão et al., 2011). Recently, the disturbed state concept was also used by Zhu et al. (2011) to compute the passive earth pressure coefficients. As this is a somewhat new concept, their study was limited to a simple problem of a smooth vertical retaining wall with a horizontal cohesionless backfill.

It is seen from the above discussion that a vast amount of literature is available in this study area. However, a majority of the literature, either theoretical or experimental, address the problem of a vertical retaining wall with a horizontal backfill (Rowe and Peaker, 1965; Shields and Tolunay, 1973; Narain et al., 1969; Fang et al., 1994 and 2002; Lancellotta, 2002; Li and Liu, 2006; Antão et al., 2011; Reddy et al., 2013). As far as the case of a sloping backfill is concerned, some important contributions are from Kerisel and Absi (1990), Fang et al. (1997), Soubra (2000), Soubra and Macuh (2002), Subba Rao and Choudhury (2005) and Benmeddour et al. (2012).

Soubra et al. (1999) applied the variational approach to the limit equilibrium method to determine the effective passive earth pressure coefficients for a cohesionless medium considering the seepage flow. For the case of no seepage flow, their analysis was reduced to the typical case of a vertical retaining wall with a horizontal cohesionless backfill. Also, in their analysis, the entire failure surface was comprised of a log spiral segment. However, their analysis was not extended for the sloping backfill case. Soubra et al. (1999) also mentioned that there is a numerical equivalence between the variational limit equilibrium approach and the upper bound theorem of limit analysis.

Later, Soubra and Macuh (2002) employed the upper bound theorem of limit analysis for the computation of active and passive earth pressure coefficients. They considered the rotational log spiral failure mechanism and the analysis was carried out for a general case of an inclined retaining wall with the frictional cohesive sloping backfill.

However, the limit analysis method is difficult to employ and it requires a professional background (Zhu, 2000). Therefore, it is decided to propose a simple but effective method for the evaluation of passive earth pressure coefficients by adopting the limit equilibrium approach with the complete log spiral failure mechanism for a vertical retaining wall with a sloping cohesionless backfill. The detailed analysis along with a complete statement of the problem is mentioned in the subsequent sections.

Statement of problem

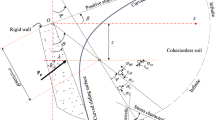
A vertical rough rigid retaining wall of height, H resting against an inclined cohesionless backfill is considered (Figure 1). The objective is to locate the critical failure surface using the limit equilibrium approach and to report the passive earth pressure coefficients, K pγ for the several possible combinations of ϕ, δ and i.

Figure 1
figure 1

Proposed failure mechanism.

Full size image

Outline of proposed analysis

Assumptions

The limit equilibrium approach is employed in the proposed analysis. However, this method itself has some limitations; especially as it involves several assumptions and due to which the solution obtained using the limit equilibrium approach may get deviated from the exact solution. Considering this fact, an attempt is made to minimise the number of assumptions involved in the analysis and therefore, to obtain the best possible upper bound solution. Also, wherever it is indispensable to make the assumptions, sufficient backup from the literature is considered for the justification of assumptions; the details of which are mentioned through the subsequent points (Ref. Figure 1).

  1. 1.

    In the proposed analysis, a complete log spiral failure surface is considered. A similar shape was considered previously by several researchers (Morrison and Ebeling, 1995; Luan and Nogami, 1997; Soubra et al., 1999; Soubra and Macuh, 2002; Li and Liu, 2006) for the computation of passive earth pressure coefficients. However, their methods of analysis were different. It should be noted that the assumption of Rankine’s (1857) passive zone is not considered herein.

  2. 2.

    The point of application of the passive thrust is assumed to be located at a distance of H/3 from the base of the wall.

  3. 3.

    The Coulomb’s law of friction is assumed to be valid along the entire failure surface.

Trial and error procedure

Considering the free body diagram of the failure wedge, JBDJ, the following forces are identified (Figure 1).

P pγ is the passive thrust on the vertical retaining wall, JB acting at a distance of H/3 from the toe, J of the wall and making an angle, δ with the horizontal. W is the self weight of the failure wedge, JBDJ. R JD is the resultant soil reaction on the failure surface, JD. As this reaction passes through the pole of the log spiral, there will not be any external unbalanced moment created due to R JD .

The angle made by the initial radius of the log spiral with the vertical retaining wall, JB is designated as θ v . Also, the angle made by the tangent to a log spiral with the horizontal at the tail end portion is considered as θ cr . The entire failure surface could be completely specified by these two angles θ v and θ cr . By specifying the angles θ v and θ cr (as mentioned in the next paragraph), and using the moment equilibrium condition about the pole of the log spiral, it is possible to compute the magnitude of K pγ for the given combination of ϕ, δ and i.

Initially this problem was solved by treating the angle θ v as the only unknown parameter and the angle θ cr was assumed to be equal to the exit angle as suggested by Rankine (1857) for the given combination of ϕ, δ and i. However, it was observed that, such type of analysis does not provide the best possible critical solution. After this confirmation, the angles θ v as well as θ cr are treated as the two unknown parameters. Then, for a specified set of ϕ, δ and i, the combination of the angles θ v and θ cr which yields the critical (minimum) passive earth pressure coefficients is searched using a trial and error procedure. For this purpose, a program is written in MATLAB and the analysis is carried out; the details of which are given in the next section.

Analysis

Geometry of the proposed failure mechanism

The detailed calculations of all the geometrical distances and angles required in the analysis are shown through the next sub-sections (Ref. Figure 2).

Figure 2
figure 2

Geometry of the proposed failure mechanism.

Full size image

Computation of angle α

The angle between the final radius, OD and the sloping backfill, BD is designated as α, which can be evaluated in terms of the angle θ cr as given below.

At the point, D

$$ {180}^0=\alpha +{\theta}_{cr}-i+{90}^0+\varPhi $$
$$ {90}^0=\alpha +{\theta}_{cr}+\varPhi -i $$
$$ \therefore \alpha ={90}^0-{\theta}_{cr}-\varPhi +i $$

Or

$$ \alpha =\frac{\pi }{2}-{\theta}_{cr}-\varPhi +i $$
(1)

Computation of angle θ m

The angle, θ m between the initial and final radii is evaluated in terms of the angles θ cr and θ v as given below.

At the point, O

$$ {90}^0={\theta}_v+{\theta}_m+\alpha -i $$
$$ {\theta}_m={90}^0-{\theta}_v-\alpha +i $$

Or

$$ {\theta}_m=\frac{\pi }{2}-{\theta}_v-\alpha +i $$
(2)

After substituting Eq. (1) into Eq. (2)

$$ {\theta}_m={\theta}_{cr}+\varPhi -{\theta}_v $$
(3)

Computation of initial and final radii

As seen from Figure 2, JB is the vertical wall of height, H retaining the inclined cohesionless backfill with the curved (log spiral) failure surface, JD; the initial and final radii of which are JO and OD respectively.

Also from the triangle JBS, the distances JS and BS are given as

$$ JS=\frac{H}{ \cos {\theta}_v} $$
(4)
$$ BS=H \tan {\theta}_v $$
(5)

Applying the Sine rule for the triangle OBS, the distances OS and OB are given as

$$ OS=BS\frac{ \sin \eta }{ \sin \gamma } $$
(6)

Substituting Eq. (5) into Eq. (6), the distance OS is rewritten as

$$ OS=H \tan {\theta}_v\frac{ \sin \eta }{ \sin \gamma } $$
(7)

and

$$ OB=BS\frac{ \cos {\theta}_v}{ \sin \gamma } $$
(8)

Substituting Eq. (5) into Eq. (8), the distance OB is rewritten as

$$ OB=H\frac{ \sin {\theta}_v}{ \sin \gamma } $$
(9)

where, the angles η and γ are evaluated as shown in the next subsection.

Now from the geometry (Figure 2), the initial radius, r 0 is given as

$$ {r}_0=JS+ OS $$
(10)

From Eqs. (4) and (7), Eq. (10) is rewritten as

$$ {r}_0=\frac{H}{ \cos {\theta}_v}+H \tan {\theta}_v\frac{ \sin \eta }{ \sin \gamma } $$
(11)

Also from the geometry of the log spiral, the final radius, r is given as (Das, 1998)

$$ OD=r={r}_0{e}^{\theta m \tan \varPhi } $$
(12)

Computation of angles η and γ

Applying the Sine rule for the triangle OBD [Figure 2]

$$ \frac{ \sin \left({\theta}_m-\gamma \right)}{BD}=\frac{ \sin \alpha }{OB}=\frac{ \sin \left(\pi -\eta -i\right)}{OD} $$
(13)

Therefore, from Eq. (13), the distance BD is given as

$$ BD=OB\frac{ \sin \left({\theta}_m-\gamma \right)}{ \sin \alpha } $$
(14)

From Eq. (13), the distance BD can also be given as

$$ BD=OD\frac{ \sin \left({\theta}_m-\gamma \right)}{ \sin \left(\pi -\eta -i\right)} $$
(15)

Substituting Eqs. (9) and (12) in Eqs. (14) and (15) respectively and then solving Eqs. (14) and (15), the angle η is obtained as

$$ \eta ={ \tan}^{-1}\left(\frac{ \sin \alpha \left({e}^{\theta m \tan \varPhi}\right)}{ \cos i. \sin {\theta}_v}- \tan i\right) $$
(16)

Also from the triangle OBS, the angle γ is given as

$$ \gamma =\frac{\pi }{2}-{\theta}_v-\eta $$
(17)

Now, Eqs. (16) and (17) are utilized to compute all the geometrical distances defined through Eqs. (6) to (12).

Self weight of the failure wedge, JBDJ

This is obtained by calculating the weight, W 1 of the log spiral part, OJD (Das, 1998) and then subtracting the weights, W 2 and W 3 of the triangular parts OBD and OBJ respectively. The total required weight of the failure wedge, JBDJ is given as (Ref. Figure 2)

$$ W={W}_1-{W}_2-{W}_3 $$
(18)

where,

$$ {W}_1=\frac{1}{4}\gamma \frac{r_0^2}{ \tan \varphi}\left({e}^{2\theta m \tan \varPhi }-1\right) $$
(19)

Also, the weights W 2 and W 3 are computed using the co-ordinate method as mentioned below.

$$ {W}_2=\frac{1}{2}\left[{x}_1\left({y}_2-{y}_3\right)+{x}_2\left({y}_3-{y}_1\right)+{x}_3\left({y}_1-{y}_2\right)\right]\gamma $$
(20)
$$ {W}_3=\frac{1}{2}\left[{x}_1\left({y}_4-{y}_2\right)+{x}_4\left({y}_2-{y}_1\right)+{x}_2\left({y}_1-{y}_4\right)\right]\gamma $$
(21)

where, the co-ordinates x 1 - x 4 and y 1 - y 4 are given in Figure 2.

Computation of passive earth pressure coefficients, K pγ

The limit equilibrium method with the complete log spiral failure surface is considered in the analysis. As mentioned by Soubra et al. (1999), the advantage of this particular shape is that the resultant of soil reaction passes through the pole of the log spiral and due to which the moment equilibrium equation about the pole of the log spiral is independent of the stress distribution along the failure surface. Therefore, this moment equilibrium equation alone could be used in order to determine the passive earth pressure coefficients.

In the proposed analysis, for the specified combination of ϕ, δ and i, the passive earth pressure coefficient, K pγ is computed by following the procedure as given below.

The forces acting on the failure wedge, JBDJ are shown in Figure 2. These forces along with their respective locations from the pole of the log spiral are also mentioned in Table 1.

Table 1 Details of all the forces acting on the failure wedge, JBDJ with their respective locations from the pole of the log spiral
Full size table

Considering ΣM @ O = 0

$$ {W}_1\overline{X_1}-{W}_2\overline{X_2}-{W}_3\overline{X_3}+{P}_{P\gamma V}{x}_2-{P}_{p\gamma H}\left(OB \sin \eta +\frac{2H}{3}\right)=0 $$
(22)

Also referring to Figure 2, the vertical and horizontal components of passive thrust are given as

$$ {P}_{p\gamma V}={P}_{p\gamma } \sin \delta $$
(23)
$$ {P}_{p\gamma H}={P}_{p\gamma } \cos \delta $$
(24)

Substituting Eqs. (23) and (24) in Eq. (22)

$$ {W}_1\overline{X_1}-{W}_2\overline{X_2}-{W}_3\overline{X_3}+\left({P}_{P\gamma } \sin \delta \right)\;{x}_2-{P}_{p\gamma } \cos \delta \left(OB \sin \eta +\frac{2H}{3}\right)=0 $$
(25)

From Eq. (25), the inclined component of passive thrust, Ppγ is given as

$$ {P}_{p\gamma}\left[ \sin \delta .{x}_2- \cos \delta \left(OB \sin \eta +\frac{2H}{3}\right)\right]=-\left({W}_1\overline{X_1}-{W}_2\overline{X_2}-{W}_3\overline{X_3}\right) $$
(26)

Or

$$ {P}_{P\gamma }=\frac{-\left({W}_1\overline{X_1}-{W}_2\overline{X_2}-{W}_3\overline{X_3}\right)}{\left[ \sin \delta .{x}_2- \cos \delta \left(OB \sin \eta +\frac{2H}{3}\right)\right]} $$
(27)

Finally, for the specified combination of ϕ, δ and i, the passive earth pressure coefficient, K pγ is computed as

$$ {K}_{p\gamma }=\frac{2{P}_{p\gamma }}{\gamma {H}^2} $$
(28)

Results and discussion

In Table 2 are reported the proposed K pγ values obtained for the several possible combinations of ϕ, δ and i.

Table 2 Proposed K pγ values for ϕ ranging from 20° to 45°, for δ/ϕ of 0, 1/3, 1/2, 2/3 and 1, and for i/ϕ of 0, 0.2, 0.33, 0.4, 0.6, 0.66, 0.8 and 1
Full size table

In order to check the validity of the proposed results, a comparison is made with the other available theoretical as well as experimental investigations and the same is discussed in detail through the subsequent paragraphs.

Comparison with existing theoretical results

In Table 3 is shown a comparison of the proposed K pγ values with those given by several other researchers. This comparison is exclusively presented for the case of a vertical retaining wall with a horizontal cohesionless backfill.

Table 3 Comparison of the proposed K pγ values with the other theoretical results for the case of a vertical retaining wall with a horizontal cohesionless backfill ( i/ϕ  = 0)
Full size table

In order to check the validity of the MATLAB program written, the analysis is carried out for a smooth (δ = 0) vertical wall with a horizontal cohesionless backfill. As seen from Table 3, for all the values of ϕ ranging from 20o -45° with δ = 0, the K pγ values obtained from the present analysis are exactly the same as given by Rankine (1857).

It is seen from Table 3 that, the proposed K pγ values agree extremely well with those given by Kerisel and Absi (1990), Soubra (2000), Antão et al. (2011) and Reddy et al. (2013); the scatter for which being less than 12% for all the combinations of ϕ and δ/ϕ values as reported in Table 3.

Lancellotta (2002) proposed the exact solution for the evaluation of passive earth pressure coefficients using the lower bound theorem of plasticity. As seen from Table 3, a fairly good agreement is seen between the proposed results and those obtained by Lancellotta (2002). However, as δ approaches towards ϕ, this difference increases with increasing ϕ values. For ϕ = 45° and δ/ϕ = 1, the scatter between the proposed results and Lancellotta’s (2002) exact solution is 35.48%.

Shiau et al. (2008) employed finite element method coupled with the bound theorems of limit analysis for the computation of K pγ values. It is observed from Table 3 that, the proposed results fall well within the lower and upper bounds of limit analysis; and therefore it can be inferred that, for the case of a vertical retaining wall resting against the horizontal cohesionless backfill and for all the combinations of ϕ and δ/ϕ values as reported in Table 3, the passive earth pressure coefficients obtained in this study are very close to the true solutions.

Kame (2012) adopted the limit equilibrium approach coupled with the Kӧtter's (1903) equation for the evaluation of K pγ coefficients. Kame (2012) fixed the unique composite (log spiral with planar) failure surface by fulfilling the horizontal as well as the vertical equilibrium conditions. Later, the moment equilibrium condition was used by him to locate the point of application of the passive thrust. As the methodology proposed by Kame (2012) was different, his analysis yields a little higher values for the case of a smooth vertical retaining wall. However, a fairly good agreement is observed between the proposed results and those presented by Kame (2012) for rest of the other combinations of ϕ and δ/ϕ values presented in Table 3.

Kumar and Chitikela (2002) and Subba Rao and Choudhury (2005) proposed the seismic passive earth pressure coefficients using the method of characteristics and the limit equilibrium method respectively. In Table 4 are compared the proposed K pγ values with those given by the aforementioned researchers for the static case.

Table 4 Comparison of the proposed K pγ values with the other theoretical investigations (a) for horizontal backfill (b) for inclined backfill
Full size table

As seen from Table 4 (a), the proposed results agree extremely well with the results of Kumar and Chitikela (2002) and Subba Rao and Choudhury (2005) except for ϕ = 40° and δ/ϕ = 1 where the proposed results are slightly higher; the scatter for which is 9.05% and 5.55% respectively.

For the static case, Subba Rao and Choudhury (2005) also presented the K pγ values for the case of an inclined backfill. As seen from Table 4 (b), the proposed results are in excellent agreement with those presented by Subba Rao and Choudhury (2005) for ϕ = 40° and i = 30°.

As already shown in Table 1, the K pγ values are obtained from the proposed analysis for the several possible combinations of ϕ, δ and i. All these K pγ values are compared with those presented by Kerisel and Absi (1990). Overall, it is observed that with the increasing ϕ and i values and as δ approaches towards ϕ, the difference between the proposed K pγ values and those given by Kerisel and Absi (1990) increases. As it is not possible to show the comparison for each and every value mentioned in Table 1, it is decided to present the comparison for the case of an inclined backfill and for ϕ values varying from 20° to 45° with δ/ϕ = 1; where the possibility of the maximum difference is more as compared to the other values of δ/ϕ.

As seen from Table 5, the proposed results agree extremely well with those given by Kerisel and Absi (1990); the maximum difference for which does not exceed 10% for all the combinations of ϕ, δ and i. It should be noted that the values reported by Kerisel and Absi (1990) are based on the solutions of Boussinesq’s equations (Benmeddour et al., 2012) whereas the proposed method is based on the simple limit equilibrium approach. Therefore, the proposed method could be considered as one of the alternatives for the evaluation of K pγ coefficients.

Table 5 Comparison of the proposed K pγ values with those given by Kerisel and Absi (1990) for ϕ ranging from 20° to 45°, for i/ϕ of 1/3, 2/3 and 1 and for δ = ϕ
Full size table

Chen and Rosenfarb (1973) presented the least upper bound solution for the K pγ coefficients using the limit analysis method. They tried six different failure mechanisms and showed that the critical solution could be obtained using the log sandwich mechanism. Later, Soubra (2000) improved the solution of Chen and Rosenfarb (1973) by adopting the kinematical analysis of upper bound theorem with the translational multi-block failure wedge mechanism. This improvement relative to the Chen and Rosenfarb’s (1973) solution was around 22% for the case of a vertical wall and for ϕ = δ = i = 45°.

Afterwards, Soubra and Macuh (2002) presented the best upper bound solution for the K pγ coefficients. They employed the upper bound theorem of limit analysis with the consideration of rotational log spiral failure mechanism. Their method attains the improvement of around 28% relative to the Soubra’s (2000) solution for the case of a vertical wall and for ϕ = δ = i = 45°.

In Figure 3 is shown a comparison of the proposed results with those given by Chen and Rosenfarb (1973), Soubra (2000) and Soubra and Macuh (2002) for ϕ = δ = 45° and for i varying from 0°- 45°.

Figure 3
figure 3

Comparison of the proposed results for K pγ with those reported by Chen and Rosenfarb ( 1973 ), Soubra ( 2000 ) and Soubra and Macuh ( 2002 ) (for ϕ  = 45° and δ/ϕ  = 1).

Full size image

As seen from Figure 3, the present solution obtained using the limit equilibrium method significantly improves the solution of Chen and Rosenfarb (1973) and Soubra (2000) by 42.79% and 17.01% respectively for ϕ = δ = i = 45°. As far as the comparison with Soubra and Macuh (2002) is concerned, it is observed that the improvement of the proposed solution relative to that of Soubra and Macuh (2002) is 0.29% and 2.97% for i = 15° and 30° respectively. However, at i = 45°, the proposed K pγ value is slightly higher; the difference for which is 9.18%. Nevertheless, it is clear from Figure 3 that the proposed results are very close to the solutions of Soubra and Macuh (2002) and therefore, it could be stated that the simple limit equilibrium method proposed herein is capable of yielding the best possible upper bound solution.

Comparison with existing experimental results

Narain et al. (1969) conducted a model study on a vertical retaining wall with a dry horizontal cohesionless backfill. For the translational wall movement, they compared their experimental results with the other available theoretical investigations. This comparison is reproduced in Table 6. The results obtained from the present theoretical investigation are also reported in Table 6.

Table 6 Comparison of the proposed K pγN values with the experimental results of Narain et al. (1969)
Full size table

As seen from Table 6, for ϕ = 38.5° and δ = 23.5°, the theories proposed by Caquot and Kerisel (1948) and Coulomb (1776) overestimate the normal component of passive earth pressure coefficients (K pγN values) while the Rankine’s (1857) theory significantly underestimates the K pγN values. However, Terzaghi’s (1941) general wedge theory and the proposed analysis make a better estimate of the passive earth pressure coefficients; the differences for which are −6.55% and +10.12% respectively.

For ϕ = 42° and δ = 23.5°, except Rankine’s (1857) theory, all the theoretical investigations overestimate the passive earth pressure coefficients. However, among the other theoretical investigations, the proposed analysis compares fairly well with the experimental results of Narain et al. (1969); the scatter for which is 34.89%.

Fang et al. (1997) conducted the experiments on a vertical rigid retaining wall with a sloping backfill. All these experiments were conducted under translational wall movement. The main purpose of their study was to access the validity of the available theoretical solutions. In Table 7 is shown a comparison of the proposed K pγN values with the experimental results of Fang et al. (1997) considering the failure criterion at a wall movement of S/H = 0.2.

Table 7 Comparison of the proposed K pγN values with the experimental results of Fang et al. (1997) for ϕ  = 30.9° and δ  = 19.2°
Full size table

As seen from Table 7, for ϕ = 30.9° and δ = 19.2° and for the backfill inclination, i varying from 0o - 20°, the proposed theoretical predictions of the K pγN values agree extremely well with the experimental results of Fang et al. (1997).

In Table 8 are compared the results of the proposed analysis with the experimental investigations of Rowe and Peaker (1965). A significant discrepancy is observed between the proposed results and those reported by Rowe and Peaker (1965). However, it may be noted that, the values reported by Rowe and Peaker (1965) are based on the experimental investigations for which the failure criterion was assumed to be at a wall movement of 5% of the wall height (i.e. S/H = 0.05); whereas as discussed earlier [discussion on comparison of the proposed results with those of Fang et al. (1997)], the proposed analysis makes a better estimate of K pγ values when the failure criterion is considered as S/H = 0.2.

Table 8 Comparison of the proposed K pγN values with the experimental results of Rowe and Peaker (1965)
Full size table

Fang et al. (2002) studied the effect of density on the passive earth pressures using the critical state concept. The experiments were conducted on a vertical retaining wall with a horizontal cohesionless backfill. In order to limit the scope of the study, all the experiments were conducted under translational wall movement.

Fang et al. (2002) observed that, for a loose backfill (D r = 38%), the limiting pressure was reached at a wall movement of S/H = 0.17. Also for a medium dense (D r = 63%) and dense backfill (D r = 80%), it was seen that the peak pressure reached at S/H = 0.03 and S/H = 0.01 respectively. Thereafter, the peak passive pressure reduces and the state of the ultimate passive thrust was observed at S/H = 0.17 for medium dense backfill whereas at S/H = 0.2 for dense backfill.

Based on these observations, Fang et al. (2002) concluded that for such a large wall movement, the critical state is reached all along the failure surface and at this state, the shear strength of the soil should be represented in terms of the residual shear strength parameter, ϕ r and not in terms of peak shear strength parameter, ϕ p .

Fang et al. (2002) compared their experimental results with the theories proposed by Coulomb (1776) and Terzaghi (1941). This comparison is reproduced in Table 9 (a) and (b). Based on this comparison, Fang et al. (2002) suggested that the ultimate passive thrust could be estimated in a better manner by adopting the critical state concept to the Terzaghi (1941) or Coulomb’s (1776) theory.

Table 9 Comparison of the proposed K pγN values with the experimental results of Fang et al. (2002) (a) Peak shear strength (b) Residual shear strength
Full size table

In order to check the validity of the proposed theory, results obtained from the present investigation are compared with the experimental results of Fang et al. (2002) for both the states of the soil; i.e. considering the peak shear strength, ϕ p as well as the residual shear strength, ϕ r in the analysis. As seen from Table 9 (a) that, for the medium dense (D r = 63%) and dense sand condition (D r = 80%), the present analysis makes a better estimate of the peak passive thrust as compared to the other two theories. Also as suggested by Fang et al. (2002), when the critical state concept is considered, all the theoretical investigations mentioned in Table 9 (b) make the excellent predictions of the ultimate passive thrust. Overall it is seen that, all the theoretical investigations mentioned in Table 9 (a) and (b) underestimate the passive pressures for the loose sand condition.

Conclusions

A limit equilibrium approach along with the complete log spiral failure mechanism is considered in the proposed analysis. The critical passive earth pressure coefficients, K pγ are computed using the optimisation technique. The main conclusions which are drawn from this study are as follows.

  1. 1.

    Generally, the limit equilibrium method yields an upper bound solution (Deodatis et al., 2014). However, an attempt is made to minimize the number of assumptions involved in the proposed analysis and therefore, the solutions for the K pγ coefficients obtained herein are very close to the best upper bound solution (by Soubra and Macuh, 2002) available in the literature so far.

  2. 2.

    The proposed results agree extremely well with most of the theoretical as well as the experimental results available in the literature.

  3. 3.

    The current practice in Geotechnical engineering is to use the earth pressure coefficients presented by Kerisel and Absi (1990). For all the possible combinations of ϕ, δ and i, an excellent agreement is seen between the proposed results and those given by Kerisel and Absi (1990). Therefore, it could be stated that, as the method developed herein is being simple to implement, it could be considered as one of the alternatives for the evaluation of passive earth pressure coefficients for a vertical retaining wall resting against the inclined cohesionless backfill.