Introduction

The first exploration of the Moon’s subsurface structure was conducted by Apollo Lunar Sounder Experiment (ALSE) (Porcello et al. 1974) aboard Apollo 17 launched in 1972. ALSE observed the reflected echoes of the radar transmitted from the mother ship orbiting above the lunar equator. Objectives of ALSE were subsurface exploration of the Moon and profiling/imaging of its surface. To achieve those, ALSE was operated at a few frequency bands of 5, 15 and 150 MHz with linearly increasing frequency (chirp signals) so as to improve the penetration depth and the ranging resolution. The largest penetration depth of approximately 1.3 km was achieved by the 5-MHz operation with an apparent resolution of 300 m. However, both the depth and the resolution are dependent on the permittivity inside the Moon. ALSE detected horizontal reflectors at an apparent depth of about 1 km beneath Mare Serenitatis and Mare Crisium (Peeples et al. 1978; Phillips et al. 1973a, b) by its limited observation from several orbits.

Lunar Radar Sounder (LRS) is a frequency-modulated continuous wave radar (Ono and Oya 2000) equipped with SELenological and ENgineering Explorer (SELENE) launched in 2007 (Kato et al. 2008). Because it was the first Japanese spacecraft to the Moon, it also has a Japanese name of KAGUYA coined after a princess believed to live on the Moon. Like ALSE, LRS also aimed at subsurface exploration of the Moon using high-frequency chirp signals ranging from 4 through 6 MHz. Major differences, however, from ALSE were its deeper penetration depth and finer resolution, which were 5 km and 75 m in vacuum and were much better than those of ALSE (Ono and Oya 2000; Ono et al. 2008). Spatial coverage of SELENE was excellent in the sense that almost all of the Moon’s surface including the far side was covered by the sounder observation from SELENE’s polar orbits with an averaged altitude of 100 km above the Moon’s surface. The total duration of the sounder observation summed up to as long as 100 days. As a result, Ono et al. (2009) reported presence of subsurface reflectors beneath several lunar maria. Apparent depths to those reflectors were a few hundreds of meters but we need to know the permittivity beneath the Moon’s surface for conversion of those values to the true depths. Furthermore, quantitative delineation of the Moon’s subsurface structure such as the true depths to the reflectors leads to understanding the origin and evolution of our Moon. It, therefore, is very important to analyze the LRS data of SELENE, which provided unprecedented radar sounding in terms of both quality and quantity.

Another example of planetary radar sounding can be found in Mars. Mars Advanced Radar for Subsurface and Ionosphere Sounding on-board Mars Express in 2003 detected presence and quantity of water ice accumulated in the Mars’s polar cap (Picardi et al. 2005; Plaut et al. 2007). Presence of water ice on Mars was further confirmed by Shallow Radar Sounder aboard Mars Reconnaissance Orbiter in 2005. Karlsson et al. (2015) found the water ice even in Mars’s mid-latitudes, while Holt et al. (2010) revealed a complex sedimentary structure beneath the Mars’s northern polar cap. These new findings are expected to elucidate the past Mars’s climate and/or traces of paleo-oceans on Mars.

On the other hand, JUpiter ICy moon Explorer (JUICE) by European Space Agency (ESA) is planned to launch in 2022. According to ESA (2014), Radar of Icy Moon Exploration aboard JUICE is going to conduct radar sounding of three icy Galilean satellites, i.e., Europa, Ganymede and Calisto so as to explore the subsurface structures, ice, water and their composition. Those sounding will be of great help for detecting subsurface oceans of those moons, which may constitute cradles for extraterrestrial lives.

Unlike the sample return missions, the past and future radar sounding from spacecraft illustrates efficiency, certainty and wide spatial coverage of planetary-scale exploration by radar sounders. In order to improve applicability of radar sounding, the LRS data have been combined with model calculation of electromagnetic (EM) wave propagation (Ono et al. 2009; Bando et al. 2015) and data by laser altimetry to estimate the thickness of the regolith layer on top of the Moon as well as to improve the ranging resolution of LRS itself by application of data processing techniques originally developed for synthetic aperture radars (Kobayashi and Ono 2007; Kobayashi et al. 2012).

Ono et al. (2009) argued the possibility of detection of the subsurface regolith layer sandwiched between basaltic layers above and below as reflectors. This is because the reflectors are detected at shallower depths than the thickness of the basaltic layers estimated by crater analyses in lunar maria (De Hon 1979; Williams and Zuber 1998). Oshigami et al. (2009) further claimed that the correlation between the surface age and detection rate of the reflectors means thicker regolith layers in older regions.

Another correlation, which is negative though, between the detection rate and surface distribution of ilmenite suggests that metals such as titanium may prevent penetration of radar pulses to interfere the reflector detection (Pommerol et al. 2010; Olhoeft and Strangway 1975; Carrier et al. 1991; Shkuratov and Bondarenko 2001). The composition of the Moon’s surface was revealed by spectroscopic studies of SELENE data. This means that both permittivity and loss tangent are important physical properties of the lunar surface, because the former determines the speed of light in the medium while the latter is defined as the ratio of the conduction current to the displacement current and plays a role in attenuation of the radar pulses. Analyses of lunar rock samples strongly imply the correlation between the loss tangent and the iron–titanium content, whereas the permittivity does not show significant dependence on rock composition. It has, in turn, a strong correlation with rock density (Olhoeft and Strangway 1975; Carrier et al. 1991; Shkuratov and Bondarenko 2001). The different dependence of physical properties of the Moon’s surface suggests regional dependence of those properties, and thus implies necessity of determination of those properties from place to place.

Porosity is another factor of consideration here. Effects of bulk porosity are inevitably included in the results of radar sounding in a form of bulk density. If we can also estimate porosity from our LRS data, it can be another important database, since Rust et al. (1999) pointed out that porosity is indicative of volcanism/tectonics of the Moon in the past.

Ishiyama et al. (2013) performed combined analyses of the delay of echoes from the subsurface reflectors and the depth of subsurface reflectors excavated at the impact craters based on data from LRS, Multiband Imager (MI) and Terrain Camera (TC) onboard the SELENE spacecraft, and determined the speed of the radar wave in uppermost layers in several maria. Based on the speed, they also estimated bulk permittivity and porosity. The estimated bulk permittivities were between 1.6 and 14.0 in Mare Serenitatis, and between 1.3 and 5.1 in Oceanus Procellarum. They also pointed out that the estimated porosity, up to about 80%, was much larger than that of Apollo soil samples, and discussed possible contributions of intrinsic voids of lava and impact-induced cracks.

In this study, we aim for estimation of the relative permittivity of the Moon’s surface by comparison of echo intensities from the surface and subsurface reflector. We will approximate the Moon by two-layer models with different permittivities and electrical conductivities in each layer and determine those model parameters by calculation of EM wave propagation according to the radar range equation. In the course of estimation, we newly introduce correlation between the electrical conductivity and the iron–titanium content to resolve the non-uniqueness appeared in previous studies. This study will also provide spatial dependence of the true depths to the detected reflectors, which may lead to better understanding of the Moon’s subsurface structures. Furthermore, those true depths can be applied to estimation of erupted lava volumes, which are useful in unraveling the Moon’s volcanism in the past. Finally, the estimated loss tangent and porosity contribute to the understandings of the Moon’s evolution and thermal history as well.

Data of Lunar Radar Sounder

A pair of mutually orthogonal 30-m dipole antennas was used for LRS. The pulse width (T), sweep rate (\(\dot{f}\)) and output power (Pt) of the transmitted chirp signals were 200 μs, 10 kHz/μs and 800 W, respectively. Each pulse was further shaped by a sinusoidal wave to minimize sidelobe effects at the time of Fast Fourier Transform (FFT) and is given by:

$$V_{\text{TX}} \left( t \right) = V_{{{\text{TX}}0}} { \sin }\left( {\pi \frac{t}{T}} \right){ \sin }\left( {\mathop \smallint \limits_{0}^{t} 2\pi \left( {f_{0} + \dot{f}t'} \right){\text{d}}t'} \right),$$
(1)

where VTX0 is the amplitude of the transmitted pulse and f0 = 4 MHz.

In general, radars are associated with a trade-off between the penetration depth, which is a function of the output power, and the ranging resolution, which is a function of the pulse width. However, the pulse compression technique using chirp signals gives us a radar with a large output power and a narrow pulse width at the same time, which improves both the penetration depth and the ranging resolution. In the case of LRS, they are 5 km and 75 m in vacuum as mentioned before, but they are also dependent on both the permittivity and the loss tangent beneath the Moon’s surface. The LRS operation throughout the mission was done by 20-Hz transmission for 72 days, while it was operated with a transmission rate of 2.5 Hz for the remaining 27 days. The LRS data are now open to the public at: http://darts.isas.jaxa.jp/planet/pdap/selene/, and all the data used in this study were downloaded from this Japan Aerospace Exploration Agency website.

A-scope data

Received echoes of LRS are not original waveforms of the reflected echoes themselves, but resampled waveforms multiplied by a local signal, which were further transferred to the Earth from the spacecraft. The observed data, therefore, are different from the original waveforms of the reflected echoes.

Specifically, let the original waveform be:

$$V_{\text{RX}} \left( t \right) = V_{{{\text{RX}}0}} { \sin }\left( {\pi \frac{{t - \tau_{\text{RX}} }}{T}} \right){ \sin }\left( {\mathop \smallint \limits_{0}^{{t - \tau_{\text{RX}} }} 2\pi \left( {f_{0} + \dot{f}t'} \right){\text{d}}t'} \right),$$
(2)

where VRX0 is the amplitude of the reflected echo and τRX is a two-way travel time of the echo, by which the apparent depth to the reflector, dA, can be given by:

$$d_{\text{A}} = \frac{{c_{0} \tau_{\text{RX}} }}{2},$$
(3)

where c0 is the speed of light in vacuum. In chirp radars, the received echoes are further mixed with an inherent local signal of the receiver typically given by the following formula:

$$V_{\text{LO}} \left( t \right) = V_{{{\text{LO}}0}} { \sin }\left( {\mathop \smallint \limits_{0}^{{t - \tau_{LO} }} 2\pi \left( {f_{0} + \dot{f}t'} \right){\text{d}}t'} \right),$$
(4)

where VLO0 is the amplitude of the local signal and VLO is the time of the mixing onset. The waveform after mixing becomes:

$$\begin{aligned} &V_{\text{RX}} \left( t \right)V_{\text{LO}} \left( t \right) \hfill \\&\quad= V_{{{\text{RX}}0}} V_{{{\text{LO}}0}} { \sin }\left( {\pi \frac{{t - \tau_{\text{RX}} }}{T}} \right){ \sin }\left( {\mathop \smallint \limits_{0}^{{t - \tau_{\text{RX}} }} 2\pi \left( {f_{0} + \dot{f}t'} \right){\text{d}}t'} \right){ \sin }\left( {\mathop \smallint \limits_{0}^{{t - \tau_{\text{LO}} }} 2\pi \left( {f_{0} + \dot{f}t'} \right){\text{d}}t'} \right) \hfill \\ &\quad= V_{RX0} V_{LO0} { \sin }\left( {\pi \frac{{t - \tau_{\text{RX}} }}{T}} \right){ \sin }\left[ {2\pi \left\{ {f_{0} \left( {t - \tau_{\text{RX}} } \right) + \frac{1}{2}\dot{f}\left( {t - \tau_{\text{RX}} } \right)^{2} } \right\}} \right]{ \sin }\left[ {2\pi \left\{ {f_{0} \left( {t - \tau_{\text{LO}} } \right) + \frac{1}{2}\dot{f}\left( {t - \tau_{\text{LO}} } \right)^{2} } \right\}} \right]. \hfill \\ \end{aligned}$$
(5)

Using a formula for the trigonometric functions, Eq. (5) can be further modified into a sum of the high-frequency part and the low-frequency part as:

$$\begin{aligned} V_{\text{RX}} \left( t \right)V_{\text{LO}} \left( t \right) &= - \frac{1}{2}V_{{{\text{RX}}0}} V_{{{\text{LO}}0}} { \sin }\left( {\pi \frac{{t - \tau_{\text{RX}} }}{T}} \right)\left( {{ \cos }\left[ {2\pi \left\{\vphantom{{+ \frac{1}{2}\dot{f}\left( {2t^{2} + \tau_{\text{RX}}^{2} - 2\left( {\tau_{\text{RX}} + \tau_{\text{LO}} } \right)t + \tau_{\text{LO}}^{2} } \right)}} {f_{0} \left( {2t - \tau_{\text{RX}} - \tau_{\text{LO}} } \right)}\right.}\right.}\right. \\&\quad \left.{\left.{\left.{+ \frac{1}{2}\dot{f}\left( {2t^{2} + \tau_{\text{RX}}^{2} - 2\left( {\tau_{\text{RX}} + \tau_{\text{LO}} } \right)t + \tau_{\text{LO}}^{2} } \right)} \right\}} \right] }\right. \\&\quad \left.{- { \cos }\left[ {2\pi \left\{ {\dot{f}\left( {\tau_{\text{RX}} - \tau_{\text{LO}} } \right)t + f_{0} \left( {\tau_{\text{RX}} - \tau_{\text{LO}} } \right) - \frac{1}{2}\dot{f}\left( {\tau_{\text{RX}}^{2} - \tau_{\text{LO}}^{2} } \right)} \right\}} \right]} \right). \end{aligned}$$
(6)

Equation (6) is then low-pass filtered with a cut-off frequency of 2 MHz to eliminate the first term in the right-hand side (R.H.S.) and resampled for 2048 points with a sampling frequency of 6.25 MHz. Figure 1 shows a sample plot of thus processed and transferred to the Earth.

Fig. 1
figure 1

An example of received waveforms. This 327.68-μs-long time-series of a reflected echo was received at 00:57:15.181 UTC on May 4, 2008 when SELENE was flying over Mare Imbrium, i.e., (40.226 N°, 345.304 E°) in the selenographic coordinate. It is filtered and resampled as described in the text

Full size image

Although filtered and resampled, the waveforms of the reflected echoes preserve the information of the two-way travel times in the form of frequency. Namely, if one makes Fourier transforms of the echoes and finds specific frequencies, fIFs, for each peak reflection, then the following relation holds:

$$f_{\text{IF}} = \dot{f}\left( {\tau_{\text{RX}} - \tau_{\text{LO}} } \right).$$
(7)

Equations (3) and (7) are combined to give:

$$d_{\text{A}} = \frac{{c_{0} \tau_{\text{RX}} }}{2} = \frac{{c_{0} \tau_{\text{LO}} }}{2} + \frac{{c_{0} f_{\text{IF}} }}{{2\dot{f}}}.$$
(8)

The first term on R.H.S. of Eq. (8) is called the ‘altitude origin for ranging’ and recorded in the LRS data together with the received waveform itself, the time stamp, the selenographic latitude/longitude and the spacecraft’s altitude. Figure 2a shows Fourier transforms of the reflected echo shown in Fig. 1. Plots of this kind are called ‘A-scope’. In Fig. 2b, three echoes are evident, one is from the Moon’s surface and the other two from the subsurface reflectors.

Fig. 2
figure 2

a A-scope of the reflected echo of Fig. 1. We used the 2nd term of Eq. (8) for x-axis instead of dA. b A zoom-in plot of a. The first three reflections including the Moon’s surface are clearly seen

Full size image

B-scan data

B-scan is a sort of dynamic spectrum using A-scope with echo intensity in color, and is called ‘radargram’, a pseudo-section of the Moon’s subsurface structure. Figure 3a shows a B-scan image over Mare Imbrium. The height of the steps seen on the Moon’s surface is approximately 75 m, which is in good harmony with the ranging resolution of LRS in vacuum.

Fig. 3
figure 3

a B-scan over Mare Imbrium at the selenographic longitude of 345.3 E°. The origin of the apparent depth is taken at the Moon’s surface assuming the averaged radius of the Moon to be 1737.4 km. b Another B-scan image at the selenographic longitude of 345.0 E°. Several strong echoes of parabolic shape are due to craters nearby. c Taking running means highlighted the subsurface reflectors especially for those starting from the horizontal black arrows, which continue to ~ 42 N°

Full size image

Reflected echoes do not always come from the nadir direction. If there is significant undulation of the Moon’s surface, the subsurface reflectors are possibly masked by strong reflected echoes on the surface. Figure 3b shows a typical example of the surface echoes, which have clear parabolic shapes because the distance between the spacecraft and the reflection points on the Moon’s surface can vary with time as the spacecraft maneuvers along its orbit.

Taking running means on the B-scan images is known to give a better protection against the surface echoes (Ono et al. 2010), provided that the subsurface reflectors are horizontal. It is also desirable to compare the running means of adjacent orbits so as to confirm the echoes coming from not ‘surface’ but ‘subsurface’. Figure 3c shows a B-scan image by taking a running mean of successive 21 raw B-scan images (Ono et al. 2010). It is noteworthy that the continuity of the subsurface reflectors is much clearer than Fig. 3a.

Methods

Two-layer model

Because the regions with two subsurface reflectors like the one shown in Fig. 3c were very limited, we decided to model the majority of the LRS data by two layers, which the transmitted waves entered normal to the surface. Figure 4 shows a schematic diagram of the assumed model. Using the radar range equation (e.g., Phillips et al. 1973a), the reflected powers, Prs and Prss, are, respectively, given by:

$$P_{\text{rs}} \left( {\varepsilon_{1} } \right) = \frac{{P_{t} G^{2} \lambda^{2} }}{{4\left( {4\pi R} \right)^{2} }}r_{01} ,$$
(9)

and

$$P_{\text{rss}} \left( {\varepsilon_{1} , \varepsilon_{2} ,\sigma_{1} } \right) = \frac{{P_{t} G^{2} \lambda^{2} }}{{4\left[ {4\pi \left( {R + R_{\text{D}} } \right)} \right]^{2} }}e^{{ - 2\omega \frac{{R_{\text{D}} }}{{c_{1} }}{ \tan }\delta_{1} }} t_{01} r_{12} t_{10} ,$$
(10)

where G, λ, ω, tan δ1, and RD are the gain of the antenna, the wavelength and angular frequency of the transmitted wave, the loss tangent of the first layer and the true thickness of the first layer, respectively. SELENE transmitted a radar pulse every 0.05 (or 0.4) second with an output power of Pt [W]. c1 is the speed of light in the first layer and given by:

$$c_{1} = \frac{1}{{\sqrt {\varepsilon_{1} \varepsilon_{0} \mu_{0} } }} = \frac{{c_{0} }}{{\sqrt {\varepsilon_{1} } }},$$
(11)

where ε0 and μ0 are the permittivity and magnetic permeability in vacuum, respectively. The loss tangent in the first layer can be written by:

$${ \tan }\delta_{1} = \frac{{\sigma_{1} }}{{\omega \varepsilon_{0} \varepsilon_{1} }},$$
(12)

as well. rij and tij (i, j = 0, 1, 2) denote the reflection and transmission coefficients at each interface and satisfy the following relation according to the Fresnel equations:

$$t_{01} = t_{10} = \frac{{4\sqrt {\varepsilon_{1} } }}{{\left( {1 + \sqrt {\varepsilon_{1} } } \right)^{2} }},$$
(13)
$$r_{01} = \left( {\frac{{1 - \sqrt {\varepsilon_{1} } }}{{1 + \sqrt {\varepsilon_{1} } }}} \right)^{2} ,$$
(14)
$$r_{12} = \left( {\frac{{\sqrt {\varepsilon_{1} } - \sqrt {\varepsilon_{2} } }}{{\sqrt {\varepsilon_{1} } + \sqrt {\varepsilon_{2} } }}} \right)^{2} .$$
(15)
Fig. 4
figure 4

The two-layer model adopted by this study. The surface and subsurface reflection are Prs (W) and Prss (W), respectively. R (m) and RD (m) are, respectively, the altitude of the spacecraft and the true depth to the subsurface reflector. Both relative magnetic permeability μ and permittivity ε between SELENE and the Moon’s surface are assumed to be unity, while those of the 1st layer are unity and ε1. The electrical conductivity of the 1st layer is σ1, and the bulk permittivity of the 2nd layer is ε2

Full size image

Equation (15) allows solutions of both \(\varepsilon_{1} > \varepsilon_{2}\) and \(\varepsilon_{1} < \varepsilon_{2}\). However, if one takes \(\varepsilon_{1} > \varepsilon_{2}\), it yields \(1 < \varepsilon_{2} < 2\), which is incompatible with the results of the Moon rock analyses (e.g., Olhoeft and Strangway 1975). It, therefore, is assumed \(\varepsilon_{1} < \varepsilon_{2}\) throughout this study. As for other parameters such as R [m], refer to Fig. 4 and its caption.

Correlation among physical properties

The previous analyses of the lunar rock samples (Shkuratov and Bondarenko 2001; Olhoeft and Strangway 1975) revealed correlation among the physical properties of the rocks such as loss tangent, density, permittivity and iron–titanium content. In short, they are expressed by the following formulae:

$${ \tan }\delta = 8.8 \times 10^{ - 4} e^{{\frac{1 - p}{2}\rho_{\text{grain}} \left( S \right) + 0.085S}} ,$$
(16)
$$\rho_{\text{grain}} \left( S \right) = 0.0165S + 2.616,$$
(17)
$$\varepsilon = 1.919^{\rho } ,$$
(18)

where S, p and ρ are the total content of titanium and iron (wt%), porosity and density (10−3 kg m−3), respectively. The subscript, grain, denotes the properties of the material itself. The porosity is defined by:

$$\rho = \rho_{\text{grain}} \left( {1 - p} \right).$$
(19)

The bulk estimate of permittivity in the 1st layer, ε1, should also be compared with εgrain.

Flow of data analysis

First, the following quantities are considered as constants: Pt = 800 W, λ = 0.06 km for the center frequency (5 MHz) for a range of 4–6 MHz and G = 1.64 from the theoretical value of the dipole antenna. It follows from Eqs. (9), (14) and observed Prs that ε1 can be determined. Equation (18) allows us to convert thus obtained ε1 to ρ.

Lawrence et al. (2002) analyzed the spectroscopic data by Lunar Prospector to yield 5° by 5° grid data of the surface content of iron and titanium as: http://pds-geosciences.wustl.edu/lunar/lp-l-grs-5-elem-abundance-v1/lp_9001/data/lpgrs_high1_elem_abundance_5deg.tab.

Substitution of the above iron and titanium contents (S) into Eq. (17) gives ρgrain. Once ρ and ρgrain are known, the porosity, p, can be estimated using Eq. (19). The remaining model parameters, σ1 and ε2, can be determined using Eqs. (10), (12) and (16) in addition to observed Prss as shown in the flowchart (Fig. 5).

Fig. 5
figure 5

The flowchart of data analysis of this study. ρ, p and δ1 denote density, porosity and loss tangent of the 1st layer, respectively, while ρgrain indicates the density pertaining to the solid material itself. As for ε1, σ1 and ε2, refer to the caption of Fig. 4

Full size image

In this analysis, we need absolute values of the echo powers in unit of W. They are determined based on the prelaunch calibration of the LRS’s receiver. Of course, it was not confirmed by the end-to-end calibration including extended antenna and spacecraft because such test was quite difficult to perform on the ground. So, we roughly check validity of the absolute calibration of the echo powers used in this study by comparison between bulk permittivities estimated in Ishiyama et al. (2013) and those in this study (see “Validity of applied methods” section).

Results

Analyzed regions

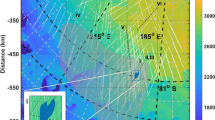
We analyzed four lunar maria, viz., Mare Serenitatis, Oceanus Procellarum, Mare Imbrium, and Mare Crisium. This is partly because clear subsurface reflectors were recognized by radargrams of several adjacent orbits in those lunar maria, and partly because it is difficult to completely eliminate the effect of surface echoes, which are especially intense in the highland areas of the Moon. Figure 6 shows the four target regions under study. Note that the values described in this section are mainly field estimates of bulk properties.

Fig. 6
figure 6

The topographic map of the northern hemisphere on the near side of the Moon. The base map was downloaded from Geospatial Information Authority of Japan (http://gisstar.gsi.go.jp/selene/Maps/Stereo_En-800.tif.zip), which is jointly operated by National Astronomical Observatory of Japan and Japan Aerospace Exploration Agency. The four red ellipses denote the location of the target areas of this study

Full size image

Estimated physical properties of all maria

Because reflected echoes from the Moon’s surface were observed everywhere, the bulk permittivity of the first layer, ε1, was estimated using Eq. (9) for 371 shots, which were approximately equivalent to one selenographic latitude. εgrain was estimated using Eqs. (17) and (18) together with the iron–titanium content of this region by Lawrence et al. (2002).

Unlike the surface echoes, the subsurface echoes were not always detected. To circumvent this, 21 stacks of A-scope were taken using the surface echo as a reference. Figure 7 shows an example of the stacked A-scope. Using those stacked echoes, estimates of ε2 were obtained in the respective latitudinal ranges using the previously estimated ε1 and Eq. (10).

Fig. 7
figure 7

The stacked A-scope. Prss indicates the location of the subsurface echo

Full size image

Radargrams of all regions are shown in Figs. 8, 9, 10 and 11, while estimates of ε1, ε2, and εgrain are plotted in Figs. 12, 13, 14 and 15 for lunar maria under study. Table 1 shows estimated porosity (%), loss tangent, electrical conductivity (S/m) in addition to the derived relative permittivities. The Fe + Ti content, S (wt%), tabulated in Table 1 was used to estimate εgrain. The table also includes the averaged apparent depths (m) as well as the calculated actual depths (m), and the number of identified subsurface echoes. In Mare Serenitatis and Oceanus Procellarum, the derived ranges of ε1 are almost compatible with those reported by Ishiyama et al. (2013): 1.6–14.0 and 1.3–5.1.

Fig. 8
figure 8

Radargrams of Mare Serenitatis for a 20–25°N and b 25–30°N

Full size image
Fig. 9
figure 9

Radargrams of Oceanus Procellarum for a 40–45°N and b 45–50°N

Full size image
Fig. 10
figure 10

Radargrams of Mare Imbrium for a 35–40°N and b 40–45°N. Averaged B-scan images are plotted

Full size image
Fig. 11
figure 11

Radargrams of Mare Crisium for a 10–15°N and b 15–20°N

Full size image
Fig. 12
figure 12

Estimates of ε1 (red), ε2 (blue) and εgrain of Mare Serenitatis for a 20–25°N and b 25–30°N. The regional representatives of εgrain = 6.49 (for 20–25°N) and 6.39 (for 25–30°N) are shown by horizontal green lines. The vertical error bars for ε1 and ε2 show 95% confidence intervals, while horizontal error bars denote their spatial extent

Full size image
Fig. 13
figure 13

Estimates of ε1 (red), ε2 (blue) and εgrain of Oceanus Procellarum for a 40–45°N and b 45–50°N. The regional representatives, i.e., εgrain = 6.41 (for 40–45°N) and 6.29 (for 45–50°N) are shown by horizontal green lines. The vertical error bars for ε1 and ε2 show 95% confidence intervals, while horizontal error bars denote their spatial extent

Full size image
Fig. 14
figure 14

Estimates of ε1 (red), ε2 (blue) and εgrain of Mare Imbrium for a 35–40°N and b 40–45°N. εgrain = 6.60 (for 35–40°N) and 6.56 (for 40–45°N) are values representative of this region, while ε1s are latitudinal averages. The vertical error bars for ε1 and ε2 show 95% confidence intervals, while horizontal error bars denote their spatial extent

Full size image
Fig. 15
figure 15

Estimates of ε1 (red), ε2 (blue) and εgrain of Mare Crisium for a 10–15°N and b 15–20°N. The regional representatives of εgrain = 6.17 (for 10–15°N) and 6.29 (for 15–20°N) are shown by horizontal green lines. The vertical error bars for ε1 and ε2 show 95% confidence intervals, while horizontal error bars denote their spatial extent

Full size image
Table 1 Summary of the data analysis
Full size table

Summary of data analyses

All results described in this section are summarized in Table 1 along with estimated ages of the lunar maria determined by crater density (Hiesinger et al., 2000; 2003; 2011). Values of the bulk permittivity show correlation with S. Table 1 also shows that each tabulated value has small spatial variation in the latitude difference of 5° to 10°. Figure 16 was created from Table 1 using values of ε1 and their 95% confidence intervals shown in Figs. 12, 13, 14 and 15. Table 1 shows a clear positive correlation of the bulk permittivity, ε1, derived in this study with the reported Fe and Ti content, S (Lawrence et al. 2002). The bulk permittivity can be expressed by ε1 = 0.297 S + 0.0107 with a correlation coefficient of R2 = 0.881.

Fig. 16
figure 16

Correlation between the bulk permittivity of the 1st layer, ε1, and the surface metal content in lunar maria under study. A regression line is drawn in red. The error bars of ε1 were calculated using values of ε1 and their 95% confidence intervals shown in Figs. 12, 13, 14 and 15

Full size image

Discussion

Validity of applied methods

Because many of A-scope data showed peaks of a single subsurface reflector that can be identified on adjacent orbits as well, it is reasonable to assume two-layer models for the LRS data. However, the analyzed results show that there are several regions of anomalously large errors for bulk permittivity. It is very difficult to consider those errors due to actual spatial variations of ε1 and ε2. It can be rather interpreted as a result of scattering of surface echoes by rugged topography. The radargrams over the large error regions suggest that those regions are characterized by combinations of intense and weak echoes. In this study, relatively flat regions were selected to yield radargrams by taking running means for better protection against rugged topography. However, the results showed that it is not sufficient for all regions. It, therefore, will be desirable to do more accurate numerical simulations of EM wave propagation by incorporating known topography on the Moon’s surface, to estimate more precise bulk permittivity over broader regions in the future. As confirmed in Subsections “Estimated physical properties of all maria” and “Summary of data analyses”, the bulk permittivities derived in Mare Serenitatis and Oceanus Procellarum in this study were almost in the range reported in Ishiyama et al. (2013).

Bulk permittivity

The derived bulk permittivity of the lunar uppermost layer was in a range from 2.96 (at Mare Imbrium) to 6.37 (at Oceanus Procellarum), which supports the actual depth to the reflectors in those maria to be around 200 m.

Olhoeft and Strangway (1975), and Carrier et al. (1991) reported that the bulk permittivity of the Moon rock samples shows values ranging from 1.1 to 11, majority of which falls between 4 and 9. However, this study yields somewhat smaller bulk permittivity not only in Mare Serenitatis and Oceanus Procellarum, which was already reported by Ishiyama et al. (2013), but also in Mare Imbrium and Mare Crisium. This can be partly attributed to the effect of porosity as discussed by Ishiyama et al. (2013), but also explained by the effect of composition, i.e., iron–titanium content.

Olhoeft and Strangway (1975) showed that the bulk permittivity is primarily a strong function of bulk density. This means that the bulk permittivity depends on not only how porous the medium in concern is, but also how dense and dielectric the rest of the medium other than cavity is. Titanium bearing minerals such as ilmenite is typical of those that have both large density and high permittivity. The good correlation between the bulk permittivity derived in this study and the known FeO + TiO2 content of the lunar maria surface shown in Fig. 16 can be regarded as possible presence of enriched titanium bearing minerals in each lunar mare such as Mare Imbrium.

The analysis method used in this study enabled us to derive bulk permittivity and porosity in wide area of multiple maria. A new suggestion brought by the comparison of porosity in multiple maria in this study will be described in the next subsection. The estimates of \(\varepsilon_{2}\) showed larger shot-by-shot scatter than \(\varepsilon_{1}\). It was assumed throughout this study that \(\varepsilon_{1} < \varepsilon_{2}\) in applying the two-layer models. However, its validity for multiple layer models should be examined in the future.

Porosity

Based on the bulk permittivity from 2.96 to 6.37, the porosity takes the values between 1.8 and 41.1%. Porosity of the Moon rock samples is less than 10% in most cases, and hence samples with porosity larger than 20% are rare (Olhoeft and Strangway 1975). However, this study yielded larger porosity, which possibly represents macroscopic (bulk) porosity rather than microscopic as was pointed out by Ishiyama et al. (2013).

Sizes of the Moon rock samples are of the order of centimeter, while the spatial resolution of LRS is at most a few tens of meters. This means that the LRS data are subject to effects of large-scale cracks. Hence, the large bulk porosity may be due to cracks by degassing at the time of volcanic eruptions, by quenching of lavas or by meteorite impacts. However, it turned out that porosity shows a weak negative correlation with formation ages of lunar maria (see Fig. 17). This may reflect effects of volcanic eruptions rather than those of meteorite impacts, because repeated meteorite impacts might have cultivated the Moon’s surface well enough to give a ‘positive’ correlation with formation age.

Fig. 17
figure 17

Correlation between the bulk porosity of the 1st layer, ρ, and the formation age of each lunar mare under study

Full size image

Loss tangent

The estimated range of loss tangent was 5.3 × 10−3–1.53 × 10−2 in this study. Olhoeft and Strangway (1975) derived a range of 7.53 × 10−3–1.92 × 10−2 at (Fe + Ti wt%) = 15 by their laboratory experiments of the Moon rock samples. The smaller loss tangent range of this study may also be attributed to the macroscopic porosity. Substitution of (Fe + Ti wt%) = 15 into Eqs. (16) and (17) yields a width of 4.6 × 10−3 for the loss tangent range, if porosity is changed from 0% through 30%. If the observed loss tangent is corrected by this range width, the two ranges, i.e., the field and laboratory ranges, agree very well. Furthermore, Bando et al. (2015) investigated the ratio between the powers of echoes from subsurface reflectors at different depths measured by LRS to yield a loss tangent range of 1.07 × 10−2–1.13 × 10−2, which corresponds to the median value of the observed loss tangent by this study. It, therefore, can be concluded that the loss tangent by this study may reflect the true loss tangent near the lunar surface (10–100 m spatial scale) with possible variations produced by macroscopic porosity.

Conclusions

Assuming incident EM waves from LRS being normal to the horizontally stratified two-layer models, bulk permittivity, porosity and loss tangent near the lunar surface were estimated using the observed LRS data by calculating EM wave propagation according to the radar range equation. Combined use of the estimated FeO + TiO2 content distribution by spectroscopy of the lunar surface (Lawrence et al. 2002) and the empirical relations among physical quantities in concern derived from analyses of the Moon rock samples (Shkuratov and Bondarenko 2001; Olhoeft and Strangway 1975) enabled unique determination of otherwise degenerated physical quantities. The results are summarized in Table 1, in which all the analyzed regions, viz., Mare Imbrium, Oceanus Procellarum, Mare Crisium and Mare Serenitatis, are included. It is obvious by the table that the actual depth to the subsurface reflectors of the Moon is around 200 m except for Mare Crisium and one part of Mare Serenitatis.

The estimates of each physical quantity do not change much within a latitudinal difference of 5° to 10°, whereas bulk permittivity shows a positive correlation with FeO + TiO2 content. Since porosity, in turn, shows a weak negative correlation with formation ages of lunar maria (see Fig. 17), it may reflect effects of volcanic eruptions rather than those of meteorite impacts. Finally, Table 1 will make a good reference for future studies, because discrepancy between the field and laboratory estimates turned out to be reconciled by the effect of porosity.